Átmenet egyikből a másikba
Ternészettudomány-tagozatos osztály voltunk. Sok felfedezés a kémiában a fizikában vagy a biológiában alig pár évvel előzte meg gimnáziumi éveinket. Az ilyenfajta felfedezések, alapvető átalakulások, vagy nevezhetjük "forradalmi" változásoknak is, a művészeti ágakban - ama négy évünknél - jóval előbb és jóval később történtek. (ez utóbbi megállapítás természetesen vitatható, kicsi és savanyú is, de saját
"kútfőmből" származó)
Sok neves matematikus és fizikus találja nehéznek, ha nem lehetetlennek, hogy olyan könyvet írjon, amelyet a nem szakmabeliek is megérthetnek.
Penrose munkái közepette időt szakított magának, és egy csodálatos könyvet írt a tájékozott laikusok számára.
A könyvből kiderül, hogy Penrose több, mint matematikai fizikus. Elsőrangú filozófus is, aki nem fél olyan problémákkal megküzdeni, amelyeket a kortárs filozófusok mint értelmetleneket hajlamosak elutasítani.
Megvan a bátorsága ahhoz is, hogy a fizikusok egy kis csoportjának növekvő ellenállása ellenére elkötelezze magát az egészséges realizmus mellett. Nemcsak arról van szó, hogy a világegyetem „ott kint” van, hanem hogy a matematikai igazságnak is megvan a saját titokzatos függetlensége és időtlensége. Mint Newton és Einstein, Penrose is mély alázattal és tisztelettel fordul mind a fizikai világ, mind a tiszta matematika platóni birodalma felé. Erdős Pál, a számelmélet kiváló művelője „Isten könyvét” szereti emlegetni, amelyben a legjobb bizonyítások mind fel vannak jegyezve. Egyes matematikusok olykor egy pillantást vethetnek egy lap töredékére. Penrose úgy véli, hogy amikor egy fizikusnak vagy matematikusnak egy hirtelen „aha” élményben van része, akkor az több, mint valamilyen „bonyolult számítás gyümölcse”. Egy pillanatra az értelem lép ekkor kapcsolatba az objektív igazsággal. Lehet-e, kérdezi Penrose, hogy Platón világa és a fizikai világ (amelyet a fizikusok már beolvasztottak a matematikába) tulajdonképpen egy és ugyanaz?
Penrose könyve sok oldalt szentel a nevezetes, felfedezőjéről, Benoit Mandelbrotról Mandelbrot-halmaznak elnevezett, fraktálszerű szerkezetnek. Noha ez statisztikus értelemben önhasonló, mert egyes részei nagyítódnak ki, végtelenül tekervényes mintája megjósolhatatlan módon változik. Penrose (velem együtt) elképzelhetetlennek tartja, hogy bárki azt gondolja, hogy ez az egzotikus rendszer nincs annyira „ott kint”, mint a Mount Everest, hogy ne olyan felfedezés tárgya legyen, mint például egy dzsungel."
...
Van-e egy szint a kvantummechanika fölött, amelybe az idő iránya és a jobb és a bal megkülönböztetése határozottan be van ágyazva? Lényegesek-e az értelem működése számára a kvantummechanika törvényei, vagy esetleg még elemibb törvények?
A két utolsó kérdésre Penrose igennel válaszol. Nevezetes elmélete a „twisztorokról” – a téridő alapjául szolgáló magasabb dimenziós, komplex térben működő, absztrakt geometriai objektumokról – túlságosan szakmai jellegű ahhoz, hogy benne lehessen ebben a könyvben. Penrose több mint két évtizede törekszik arra, hogy a kvantummechanika mezőinél és részecskéinél mélyebb tartományba ásson le. Háromféle osztályba sorolja az elméleteket, ezek a szuper, a hasznos és a kísérleti, és a twisztorelméletet szerényen a kísérleti osztályba teszi, a mostanában hevesen vitatott szuperhúrok és más nagy egyesítési rendszerek mellé."
"Penrose eredményei a matematikában és a fizikában – amelyeknek csak kis töredékét érintettem – a létezés titka és szépsége iránti, egész életen át tartó kíváncsiság szüleményei. Kisujja azt mondja neki, hogy az emberi elme több, mint parányi huzalok és kapcsolók puszta gyűjteménye. A prológus és epilógus Adamja részben szimbóluma a tudatosság hajnalának az érzelmi élet lassú fejlődésében. Számomra ő is Penrose – a gyermek a harmadik sorban, a MI élharcosai mögött –, aki ki meri mondani, hogy az EMI császárai meztelenek. Penrose sok gondolatát átszövi a humor, ezen az egyen azonban nincs mit nevetnünk.
Martin Gardner
Mandelbrot
Mandelbrot-halmaz
fraktálok
A régi számítógépe merevlemezén őrzök egy általa letöltött tanulmányt a fraktálokról.
...
Mándy Iván egyik novellájában - úgy rémlik, de most nem tudom megtalálni - szerepel egy finom, jó illatú öreg hölgy: a neve Mandelbrot néni.
1. Lehet-e egy számítógépnek esze?
A Turing-próba
Hajlok általános elvként azt hinni, hogy az utánzat, bármilyen ügyes is, elég ügyes próbával mindig felismerhető – bár ez inkább hit (vagy tudományos optimizmus) dolga, mint bizonyított tény. Így mindent egybevéve kész vagyok a Turing-próbát saját területén nagyjából érvényesnek elfogadni. Azaz, ha a számítógép valóban képes volna minden feltett kérdést úgy megválaszolni, hogy az nem különbözne attól, ahogy egy ember válaszolna rájuk – és ezáltal alaposan3 és következetesen a bolondját járatná kérdezőnkkel – akkor ellenkező bizonyítékok hiányában az volna a sejtésem, hogy a számítógép valóban gondolkodik, érez stb. A „bizonyíték”, „valóban” és „sejtés” szavak használatához tartozik, hogy amikor a gondolkodásra, érzésre, értelemre vagy különösen a tudatosságra hivatkozom, akkor nem csupán a nyelvi hagyományoknak engedelmeskedem, hanem ezekkel a fogalmakkal objektív „dolgokat” jelölök, amelyek jelenlétét vagy hiányát fizikai testekben megpróbáljuk bizonyítani! Ezt nagyon lényeges pontnak tekintem. Amikor az ilyen tulajdonságok jelenlétét próbáljuk észrevenni, akkor a számunkra elérhető összes bizonyíték alapján teszünk sejtéseket. (Ez elvileg nem különbözik mondjuk attól, ahogy egy csillagász próbálja egy távoli csillag tömegét megállapítani.)
Miféle ellenbizonyítékokat kellene esetleg figyelembe vennünk? Erről előre nehéz szabályokat lefektetni. Világossá akarom azonban tenni, hogy azt a puszta tényt, hogy a számítógép tranzisztorokból, drótokból és hasonlókból készíthető, nem pedig neuronokból, véredényekből stb., önmagában nem tekintem ellenbizonyítéknak. Az jár a fejemben, hogy valamikor a jövőben kifejlődhet a tudatosság egy sikeres elmélete – sikeres abban az értelemben, hogy összefüggő és megfelelő fizikai elmélet, amely szépen összeillik a fizika egyéb részeivel, és amelynek jóslatai pontosan egybevágnak az emberi lények elképzeléseivel arról, hogy ők maguk mikor és milyen mértékben látszanak tudatosnak –, és hogy ez az elmélet valóban tartalmazhat állításokat számítógépünk feltételezett tudatosságáról. Még egy „tudatosságdetektort” is elképzelhetünk, amelyet ezen elmélet elvei szerint építettek, és amelyik tökéletesen megbízható az emberre nézve, de amelyik egy számítógép esetén egy Turing-próba eredményeitől eltérő eredményeket ad. Ilyen körülmények között nagyon óvatosan kellene értelmezni a Turing-próbák eredményeit. Nekem úgy tetszik, az, hogy hogyan vélekedik valaki a Turing-próba alkalmasságának kérdéséről, részben attól függ, hogyan képzeli el az illető a tudomány és technika fejlődését. E megfontolások némelyikére a későbbiekben még vissza kell majd térnünk.
Korai még, de eszembe jut Asimov R.Daneel Olivaw-ja és legfőképpen Giscardja.
Az „öröm” és a „fájdalom” egy MI-megközelítése
Mindamellett hiszem, hogy a MI komoly dolog, amelyet méltányolni kell, és amelyre figyelni kell. Nem akarom ezzel azt mondani, hogy a valódi intelligencia szimulálásában már nagyon sokra, ha egyáltalán valamire, jutottak. Nem szabad azonban elfelejtenünk, hogy a tárgykör még nagyon fiatal. A számítógépek gyorsabbak lesznek, nagyobb gyors hozzáférésű tárolóik, több logikai egységük lesz, és nagyszámú műveletet fognak párhuzamosan elvégezni. Javulás várható a logikai tervezésben és a programozási technikában is. Ezek a gépek, a MI-filozófia eszközei, technikai képességeikben hatalmasat fognak javulni. Mi több, maga a filozófia belsőleg nem abszurd. Az emberi intelligencia talán valóban nagyon pontosan utánozható lesz elektronikus számítógépekkel – lényegében a maiakkal, amelyek a már megértett elvekre alapoznak, de sokkal nagyobb kapacitásuk, sebességük stb. lesz, ami az évek során majd biztosan bekövetkezik. Ezek az eszközök talán még valóban intelligensek is lesznek; talán gondolkodni, érezni fognak, eszük lesz. Vagy talán nem, és új elvekre lesz szükség, amelyek ma még teljesen hiányoznak. Ez olyan nagy kérdés, hogy nem lehet könnyedén elutasítani. Megpróbálok bemutatni olyan bizonyítékokat, amiket a legjobbaknak látok. Végül pedig előadom saját javaslataimat..
Az EMI és Searle kínai szobája
Searle fenntartja, hogy ha az emberi agy (amelynek lehet esze) és az elektronikus számítógép (amelynek szerinte nem lehet esze) egyaránt képes lenne végrehajtani ugyanazt az algoritmust, akkor működésük között csupán anyagi felépítésükben lenne különbség. Azt állítja, de az okokat nem képes megmagyarázni, hogy a biológiai objektumoknál (agyaknál) lehet „szándékosság” és „szemantika”, amit ő a szellemi tevékenység meghatározó jellemzőinek tart, míg az elektronikusoknál nem. Számomra ez önmagában nem jelöli ki az utat az ész valamilyen hasznos, tudományos elmélete felé. Mi az olyan különleges a biológiai rendszereknél, eltekintve talán a „történelmi” módtól, ahogy fejlődtek (és attól a ténytől, hogy mi emberek történetesen ilyen rendszerek vagyunk), ami olyan objektumokká teszi azokat, hogy elérhetik a szándékosságot vagy a szemantikát? Az állítás nekem gyanúsan hasonlít egy dogmatikus kijelentésre, talán nem is kevésbé dogmatikus, mint az EMI azon állításai, amelyek szerint egy algoritmusnak puszta lejátszása elővarázsolhatja a tudatosság állapotát!
Véleményem szerint Searle-t, és nagyon sok más embert is, félrevezették a számítógépes szakemberek. Őket pedig a fizikusok. (Ez nem a fizikusok bűne. Még ők sem tudnak mindent!) Úgy látom, széles körű az a hiedelem, hogy valójában „minden digitális számítógép”. Szándékom, hogy megpróbáljak ebben a könyvben rámutatni, miért és talán hogyan nem szükségszerűen ez a helyzet.
Amennyire ki tudom bogozni, az EMI-filozófia alapját szolgáló egyik legfontosabb tényező ez az ekvivalencia a fizikai számolóeszközök között. E nézőpont szerint a hardver nem nagyon fontos (esetleg teljesen lényegtelen), a szoftver, azaz a program vagy az algoritmus az egyetlen lényeges alkotórész. Én azonban úgy látom, hogy vannak más fontos alaptényezők is, amelyek többnyire a fizika irányából jönnek. Megpróbálom vázolni, mik lehetnek ezek a tényezők.
Mi az, ami megadja egy személy egyedi azonosságát? Maguk az atomok lennének, amelyek testét alkotják? Függ-e az egyén azonossága az adott elektronoktól, protonoktól és más részecskéktől, amelyekből ezek az atomok összetevődnek? Legalább két okot lehet mondani, miért nem lehet ez így. Elsősorban, bármelyik élő személy testének anyaga állandóan cserélődik. Ez különösen áll az agy sejtjeire, annak ellenére, hogy a születés után új agysejtek többé nem keletkeznek. Minden élő sejtben (az agysejteket is beleértve) az atomok hatalmas többsége – tulajdonképpen testünk teljes anyaga – a születés után sokszor kicserélődik.
A második ok a kvantumfizikából jön – és különös irónia, hogy szigorúan véve ellentmondásban áll az elsővel! A kvantummechanika szerint (erről többet majd a 6. fejezetben fogunk látni) bármely két elektron szükségszerűen tökéletesen azonos kell legyen, és ugyanez érvényes bármely két protonra és bármely két, azonos típusú részecskére. Nem csak arról van szó, hogy nincs mód a részecskék megkülönböztetésére, az állítás ennél lényegesen erősebb. Ha egy ember agyának egy elektronját kicserélnék egy tégla egy elektronjával, akkor a rendszer állapota pontosan14 ugyanaz az állapot lenne, mint előtte, nem csupán attól megkülönböztethetetlen! Ugyanez érvényes a protonokra és bármilyen fajta részecskékre, egész atomokra, molekulákra stb. Ha egy ember teljes anyagi tartalmát kicserélnék a házának tégláiban lévő megfelelő részecskékkel, akkor szigorú értelemben az égvilágon semmi sem történne. Az embert a házától az a minta különbözteti meg, ahogyan alkotórészei elrendeződnek, nem pedig maguknak az alkotórészeknek az egyénisége.
Hardver és szoftver
Ezzel kapcsolatos egy gyakran tárgyalt ötlet, a tudományos-fantasztikus irodalom távfuvarozó gépe.15 Az elképzelés szerint ez a „szállítás” egyfajta módja, mondjuk egyik bolygóról egy másikra, de hogy valójában lehetséges-e, erről vita folyik. Ahelyett, hogy egy űrhajó a „rendes” módon fizikailag szállítaná, a leendő utazót tetőtől talpig letapogatják, és a legteljesebb részletességgel feljegyzik a testében lévő minden atom és minden elektron pontos helyzetét és teljes leírását. Mindezt az információt elektromágneses jellel (fénysebességgel) átsugározzák a rendeltetési helyre, a távoli bolygóra. Ott az információt összegyűjtik, és arra használják, hogy segítségével összeállítsák az utazó pontos másolatát, egész memóriájával, szándékaival, reményeivel és legmélyebb érzéseivel együtt. Ennyit mindenképpen elvárnak, minthogy az agy állapotának minden részletét hűen feljegyezték, átküldték és rekonstruálták. Feltételezve, hogy a mechanizmus működik, az utazó eredeti példánya „nyugodtan” megsemmisíthető. A kérdés természetesen az: valóban utazási módszer-e ez egyik helyről a másikra, vagy csupán egy másolat készítése és az eredeti meggyilkolása? Kész volna-e Ön használni az „utazásnak” ezt a módját – feltéve, hogy kimutatták róla, hogy saját keretein belül teljesen megbízható? Ha a távfuvarozás nem utazás, akkor milyen elvi különbség mutatkozik közte és aközött, ha csak szépen átsétálunk egyik szobából a másikba? Az utóbbi esetben nem arról van-e szó, hogy valakinek az atomjai az egyik pillanatban megadják az atomok következő pillanatbeli helyére vonatkozó információt? Végül is láttuk, hogy az egyes atomok azonossága megőrzésének nincs jelentősége, sőt még értelmetlen is az egyes atomok azonosságáról beszélni. Nem képez-e az atomoknak minden mozgó alakzata egyfajta információs hullámot, amely átterjed egyik helyről a másikra? Hol van a lényeges különbség a hullámok terjedése között, aminek segítségével a szokásos módon lehet leírni utazónk átballagását egyik szobából a másikba, és aközött, ami a távfuvarozó műszerben végbemegy?
Van-e bármi olyan a fizika törvényeiben, ami elvileg lehetetlenné teszi a távfuvarozást? Másrészt esetleg az a helyzet, hogy elvileg semmi nem szól egy személynek és egy személy tudatának ilyen átvitele ellen, de a „másoló” folyamat szükségszerűen megsemmisítené az eredetit? Lehet, hogy a két életképes példány megőrzése az, ami elvileg lehetetlen? Úgy vélem, hogy bármily szokatlanok is e gondolatok, talán van valami jelentőségük, ki lehet hámozni belőlük valamit a tudat és egyéniség fizikai természetére vonatkozóan. Azt hiszem, támpontot nyújtanak, jelzik a kvantummechanika fontos szerepét a tudati jelenségek megértésében. De ne siessünk előre! Vissza kell majd térnünk ezekre a dolgokra, miután megvizsgáltuk a kvantumelmélet szerkezetét a 6. fejezetben.
Egyelőre azonban fogadjuk el azt a (mindennapos) nézetet, hogy minden lényeges fizikát lehet digitális számításokkal modellezni. Ekkor a „műveleti” az egyetlen reális feltevés (az időre és a számítások terjedelmére vonatkozó kérdésektől eltekintve), azaz hogy ha valami teljesen hasonlóan cselekszik, mint egy tudatos dolog, akkor el kell fogadnunk, hogy magát annak a dolognak is „érzi”.
Az EMI-szemlélet azt tartja, hogy „csupán” hardverkérdés lévén, minden, az agy munkája során ténylegesen előhívott fizika szükségszerűen szimulálható kell legyen megfelelő átalakító szoftver bevezetésével. Ha elfogadjuk a műveleti nézőpontot, akkor a kérdés az univerzális Turing-gépek ekvivalenciáján és azon a tényen alapszik, hogy egy ilyen géppel valóban minden algoritmus végrehajtható – együtt a feltevéssel, hogy az agy tényleg valamilyen algoritmus szerint működik.
2. Algoritmusok és Turing-gépek
Az algoritmusfogalom háttere
Mi pontosan egy algoritmus vagy egy Turing-gép, vagy egy univerzális Turing-gép? Miért annyira alapvetőek e fogalmak annak modern megítélésében, hogy mi képezhet „gondolkodó eszközt”? Vannak-e abszolút korlátai annak, mit érhet el elvileg egy algoritmus? Hogy ezeket a kérdéseket megfelelő formában tudjuk felvetni, meg kell vizsgálnunk az algoritmus és a Turing-gépek fogalmát kicsit részletesebben.
Az „algoritmus” szó a kilencedik századbeli perzsa matematikus, Abu Dzsáfár Mohammed ibn Músza al-Hvárizmi nevéből származik, aki i. sz. 825 körül nagy hatású matematikai tankönyvet írt „Kitab al jabr w’al-muqabala” címmel. Az „algoritmus” ma használatos, a korábbi és pontosabb „algorizmus”-tól eltérő alakja valószínűleg az „aritmetika” szóhoz való társítás következménye. (Érdemes megjegyezni, hogy az „algebra” szó az említett könyv címében előforduló arab „al jabr” szóból származik.)"
"Algoritmusokra példákat azonban al-Hvárizmi könyvénél már sokkal korábban ismertek. Az egyik legnépszerűbb az ókori görög időkből (kb. i. e. 300-ból) származó, ma euklideszi algoritmus néven ismert eljárás, két szám legnagyobb közös osztójának meghatározására.
Eukleidész algoritmusa csak egy a számos, gyakran nagyon régóta ismert, algoritmikus eljárás közül, amelyek a matematika minden területén megtalálhatóak. Figyelemre méltó azonban, hogy algoritmusok speciális példáinak ókori történeti eredete ellenére az általános algoritmusfogalom pontos megalkotása csak ebben a században történt meg. Valójában e fogalom változatos alternatív leírásait adták meg, mindet az 1930-as években. Ezek közül a legközvetlenebb, a leginkább meggyőző és történetileg is a legfontosabb az, amelyik a Turing-gép néven ismert fogalmat használja.
...
Amit egy Turing-„gépről” tudnunk kell, hogy az egy darab „absztrakt matematika”, és nem fizikai objektum. A fogalmat az angol matematikus, kódfejtő szakértő és úttörő számítógéptudós, Alan Turing vezette be 1935–36-ban (Turing 1937), hogy segítségével megbirkózzon egy nagyon széles körű, az eldönthetőségi probléma (Entscheidungsproblem) néven ismert kérdéssel, amelyet a nagy német matematikus, David Hilbert vetett fel.
Absztrakt, elvont, nem anyagi létező. Platon világa.
...
Hilbert nem kevesebbet keresett, mint egy általános algoritmikus eljárást a matematikai problémák megoldására, vagy inkább választ arra a kérdésre, hogy ilyen eljárás elvileg létezhet-e vagy sem. "
"Hilbertnek volt olyan programja is, hogy a matematikát egyszer s mindenkorra lefektetett axiómákkal és eljárási szabályokkal megtámadhatatlan, tökéletes alapra helyezze, de mire Turing nagy munkájával előállt, addigra erre a programra már megsemmisítő csapást mért egy meglepő tétel, amelyet 1931-ben bizonyított be a briliáns osztrák logista, Kurt Gödel.
...
"Hilbertnek az a problémája, amellyel Turing foglalkozott (az eldönthetőségi probléma), túlment a matematika minden speciális, axiomatikus rendszerek formájában való megfogalmazásán. A kérdés a következő volt: van-e általános, mechanikus eljárás, amellyel elvileg megoldható lenne a matematika minden (alkalmasan meghatározott osztályba tartozó) problémája, egyik a másik után?"
...
"A kérdés megválaszolásának nehézsége részben annak eldöntése volt, mit értsünk „mechanikus eljárás” alatt. E fogalom kívül esett az akkori idők rendes matematikai elképzelésein. Hogy ezzel megmérkőzzön, Turing megpróbálta elképzelni, hogyan lehetne a „gép” fogalmát formálissá tenni, működését elemi egységekre bontani. Világosan látszik, hogy Turing saját értelmezésében az emberi agyat is a „gépek” egyikének tekintette, úgyhogy bármilyen tevékenységet hajtsanak is végre a matematikával foglalkozó emberek, amikor matematikai problémáikkal birkóznak, ezekre is a „mechanikus eljárás” címkéjét ragasztotta volna."
...
"Turing ténylegesen megmutatta, hogy vannak olyan tökéletesen jól meghatározott matematikai műveletek, amelyeket semmilyen közönséges értelemben nem lehet mechanikusnak nevezni! Van talán némi irónia abban, hogy éppen Turing munkájának ez az oldala jelenthet közvetett módon egérutat számunkra, amelyen kiléphetünk a szellemi jelenségek természetének Turing-féle koncepciójából."
Turing koncepciója
"Próbáljunk elképzelni egy gépet, amely valamilyen (végesen definiálható) számítási eljárást hajt végre. Milyen lenne ennek általános alakja? Fel kell készülnünk arra, hogy egy kicsit idealizáljunk, és ne törődjünk túl sokat a gyakorlati dolgokkal: valójában egy matematikailag idealizált „gépről” gondolkodunk. Gépünktől azt várjuk, hogy különböző lehetséges állapotai egy diszkrét sorozatot alkossanak, számuk véges (bár esetleg nagyon nagy szám) legyen. Ezeket a gép belső állapotainak nevezzük. Nem akarjuk azonban korlátozni a számítások méretét, amelyeket gépünk elvileg végre fog hajtani. "
...
"Így bár gépünknek véges számú belső állapota van, tudnia kell kezelni olyan adatbevitelt is, amely méretében nem korlátozott. "
...
"Mivel gépünknek csak véges számú különböző belső állapota van, nem lehet tőle elvárni azt, hogy az összes külső adatot vagy számításainak összes eredményét „magában hordozza”. Ehelyett az adatoknak vagy az előző számításoknak csak azokat a részeit kell vizsgálnia, amelyekkel közvetlenül foglalkozik, ezeken kell elvégeznie a szükséges műveletet."
...
"Lejegyezheti, esetleg a külső tárolóterületen a művelet lényeges eredményeit, azután pontosan meghatározott módon áttérhet feladatának következő szakaszára. A korlátlan bevitel, számítási terület és kivitel az, ami elárulja, hogy csak egy matematikai idealizációról beszélünk, és nem valami olyanról, amit a gyakorlatban valóban meg lehetne valósítani "
...
"akármilyen szemmel nézünk is rá, Turing idealizációját valóban figyelemreméltóan jól megközelítik a mai elektronikus számítógépek."
...
"az eszköz minden bevitelét környezetéből kapja. Úgy használja a környezetet, mint saját „durva papírját”. Kivitelét végül ugyanebbe a környezetbe írja ki.
Turing leírásában a „szalag” négyzeteknek egy lineáris sorozatából áll, amely mindkét irányban végtelen. A szalagon minden négyzet vagy üres, vagy egyetlen jelet tartalmaz.17 A megjelölt és jelöletlen négyzetek használata azt mutatja, hogy megengedjük „környezetünk” (azaz a szalag) lebontását, és (a folytonossal szemben) diszkrét elemekkel való leírását. Ez ésszerűnek látszik, ha azt kívánjuk, hogy eszközünk megbízható és abszolút meghatározott módon működjék. Megengedjük azonban, hogy ez a „környezet” (potenciálisan) végtelen legyen, ami az általunk használt matematikai idealizáció sajátossága, de a bevitel, a számítás és a kivitel bármelyik speciális esetben mindig véges kell maradjon. Így bár a szalagot végtelen hosszúnak vesszük, csak véges számú jel lehet rajta. Egy bizonyos ponton túl mindkét irányban teljesen üresnek kell lennie."
...
"Annak teljes magyarázata, miért csinálja meg az EUC (vagy az UN×2) azt, amit elvárunk tőle, tartalmaz bizonyos finomságokat, és sokkal bonyolultabb lenne elmondani, mint amennyire bonyolult a gép maga – nem szokatlan tulajdonsága ez a számítógépprogramoknak! (Hogy miért csinálja egy algoritmikus eljárás meg azt, amit feltételeznek róla, ennek teljes megértéséhez meglátások kellenek. Algoritmikusak-e maguk a „meglátások”? Ez olyan kérdés, amely a későbbiekben fontos lesz számunkra.)"
A numerikus adatok kettes rendszerbeli kódolása
...
"A fentiek adnak némi elképzelést arról, mire képesek a Turing-gépek nagyon elemi szinten. Ahogy az várható, ezek a gépek roppant bonyolulttá válhatnak és ténylegesen azzá is válnak, ha némileg összetett műveleteket kell végrehajtaniuk. Mi tehát végül az ilyen eszközök működési területe? Ezt a kérdést vizsgáljuk a következőkben."
A Church-Turing tétel
..."Még továbbmenve, olyan Turing-gépeket is lehet készíteni, amelyeknél nincs előre rögzítve, milyen aritmetikai műveletet kell végrehajtani, de az erre szolgáló utasítások rajta vannak a szalagon. Lehet, hogy valamelyik lépésben az éppen elvégzendő művelet függ valamelyik olyan számítás eredményétől, amelyet a gépnek egy korábbi szakaszban kellett elvégeznie. („Ha ennek a számításnak az eredménye nagyobb, mint ez és ez, akkor csináld ezt; egyébként csináld azt.”) Ha egyszer meggyőződtünk arról, hogy lehet olyan Turing-gépeket csinálni, amelyek aritmetikai vagy egyszerű logikai műveleteket végrehajtanak, akkor könnyebben el tudjuk képzelni, hogyan lehet velük bonyolultabb, algoritmikus természetű feladatokat elvégeztetni. Ha az ember játszott már ilyen dolgokkal, akkor könnyen megnyugszik abban, hogy egy effajta géppel bármilyen mechanikus műveletet el lehet végeztetni! Ésszerűnek látszik matematikailag úgy definiálni egy mechanikus műveletet, mint amit egy ilyen gép végre tud hajtani. Az „algoritmus” főnevet és a „kiszámítható”, „rekurzív” és „végrehajtható” mellékneveket a matematikusok mind az olyan mechanikus műveletek megjelölésére használják, amelyeket ilyen típusú elméleti gépekkel – a Turing-gépekkel – végre lehet hajtani. Amennyiben egy eljárás elég világos és mechanikus, akkor joggal gondolhatjuk, hogy valóban lehet találni olyan Turing-gépet, amely végrehajtja azt. "
"Másrészről esetleg még úgy érezhető, hogy az ilyen gépek tervezését talán szükségtelenül korlátoztuk. Első pillantásra ilyen korlátozásnak tűnik az, hogy az eszköz egyszerre csak egy bináris jegyet (0-t vagy 1-t) olvashat el, és hogy egyszerre csak egy lépésnyit mozdulhat el, és csak egyetlen egydimenziós szalag mentén."
"Láthatjuk, hogy amíg a Turing-gép talál üres helyet az adott szalagon, addig nincs szükség egynél több szalagra. Ehhez viszont szükség lehet arra, hogy a szalagon az adatokat áthelyezze egyik helyről a másikra. Lehet, hogy ez „rossz hatásfokú”, de nem korlátozza azt, ami elvileg elérhető.20 Hasonlóképpen, elvileg nem nyerünk semmit több Turing-gép párhuzamos működtetésével (ami az utóbbi évek divatossá vált elképzelése az emberi agy jobb modellezésének szándékától hajtva), bár bizonyos körülmények között a működési sebesség megnövekedhet. Két, egymással közvetlenül nem kommunikáló, különálló géppel nem lehet többet elérni, mint két egymással kommunikálóval, ha pedig kapcsolat van közöttük, akkor valójában egyetlen gépnek számítanak!"
"Mi a helyzet Turingnak azzal a megszorításával, hogy a szalag egydimenziós? Ha úgy gondolunk a szalagra, hogy az a „környezetet” képviseli, akkor lehet, hogy jobban szeretnénk, ha nem egydimenziós lenne, hanem egy sík felület, esetleg háromdimenziós szerkezet. Egy sík felület látszólag közelebb állhat ahhoz, ami egy „folyamattáblához” szükséges (például az euklideszi algoritmus működésének előbbi leírásában).21 Elvi nehézség azonban nincs abban, hogy egy folyamatábra működését „egydimenziós” formában (például a táblázat közönséges szóbeli leírásával) adjuk meg. A kétdimenziós síkbeli megjelenítés csak saját kényelmünket és a könnyebb érthetőséget szolgálja, és nem befolyásolja azt, hogy elvileg mit lehet elérni. Egy jel vagy objektum helyzetét a kétdimenziós síkon, sőt a háromdimenziós térben is mindig világos módon fel lehet jegyezni egydimenziós szalagra. (Egy kétdimenziós sík használata valójában tökéletesen ekvivalens két szalag használatával. A két szalag szolgáltatná a két „koordinátát”, amelyre szükség van a kétdimenziós sík egy pontjának megadásához; hasonlóképpen három szalag elő tudja állítani a háromdimenziós tér egy pontjának koordinátáit.) Ez az egydimenziós kódolás megint „rossz hatásfokú” lehet, de ez nem befolyásolja azt, hogy mit lehet elvileg elérni."
Vonal.Sík.Tér
"Ez jelentősen megerősítette azt a nézőpontot, amely a Church–Turing-tétel néven vált ismertté, hogy a Turing-gép (vagy az azzal ekvivalens) fogalom valójában definiálja azt, amit matematikailag algoritmikus (végrehajtható, rekurzív, mechanikus) eljárás alatt értünk. ...
ma:
"arra irányul a figyelem, hogy vajon a valódi fizikai rendszerek (ideértve feltehetően az emberi agyat is) – amelyek pontos fizikai törvények szerint működnek –, többet, kevesebbet vagy pontosan ugyanazokat a logikai és matematikai műveleteket képesek-e végrehajtani, mint a Turing-gépek. Én nagyon boldogan elfogadom a Church–Turing-tétel eredeti matematikai alakját. A valóságos fizikai rendszerek viselkedésével való kapcsolata viszont külön probléma, amely könyvünkben később az egyik fő kérdés lesz.
Számok, amelyek nem természetes számok
"Az előző vizsgálatban természetes számokkal végzett műveleteket néztünk, és megjegyeztük azt a figyelemre méltó tényt, hogy egy önmagában álló Turing-gép tetszőlegesen nagy természetes számokat képes kezelni annak ellenére, hogy minden gépnek meghatározott, véges számú, különböző belső állapota van."
"Gyakran kell azonban bonyolultabb számokkal dolgozni, negatív számokkal, törtekkel vagy végtelen tizedes törtekkel."
"A negatív számok és a törtek (például az olyan számok, mint a –597/26) könnyen kezelhetők Turing-gépekkel, és a számlálók és nevezők akármilyen nagyok lehetnek."
"A negatív számok és a törtek így természetes számok véges sorozataival kezelhetőek, ezért a kiszámíthatóság általános kérdését illetően semmi újat nem hoznak.
"Hasonlóképpen nem adnak semmi újat a tetszőleges hosszúságú véges tizedes törtek sem, mivel ezek csupán a törtek speciális esetei. "
"A valóságban bizonyára létezik olyan Turing-gép, amely ebben az értelemben kiadja a π teljes tizedes tört kifejtését, bár egy kissé bonyolult volna explicit módon kidolgozni azt. Hasonló megjegyzés érvényes sok más irracionális számra, mint például a
search = 1, 414213562…-re. A helyzet azonban az, hogy egyes irracionális számok (figyelemre méltóan) egyáltalán nem állíthatók elő semmiféle Turing-géppel, amint azt a következő fejezetben látni fogjuk. Azokat a számokat, amelyeket elő lehet ilyen módon állítani, kiszámíthatóaknak nevezik (Turing 1937). Amelyeket nem lehet (a hatalmas többség ilyen!), azok a nem kiszámíthatóak."
"Erre és rokon problémákra a későbbi fejezetekben vissza fogok térni. Lesz bizonyos jelentősége számunkra azzal a kérdéssel kapcsolatban, hogy vajon egy valóságos fizikai objektum (például az emberi agy) fizikai elméleteink szerint megfelelően leírható-e kiszámítható matematikai szerkezetekkel kifejezve.
A kiszámíthatóság kérdése a matematikában általánosságban fontos. Nem úgy kell gondolni rá, mint ami csak számokra mint olyanokra vonatkozik. Lehetnek olyan Turing-gépek, amelyek közvetlenül matematikai képletekkel, például algebrai vagy trigonometrikus kifejezésekkel dolgoznak, vagy amelyek a kalkulus formális manipulációit csinálják végig. "
"Nincs másra szükség, mint az összes előforduló matematikai szimbólum 0-kból és 1-ekből álló sorozatokba való pontos kódolásának valamilyen formájára, és ekkor a Turing-gép fogalma alkalmazható. Végül is ez járhatott Turing fejében, amikor nekilátott az eldönthetőségi probléma megoldásához, amely algoritmikus eljárást keres általános természetű matematikai kérdések megválaszolására."
Az univerzális Turing-gép
Nem írtam még le az univerzális Turing-gép fogalmát. Az elvet nem túl nehéz megadni, bár a részletek bonyolultak. Az alapeszme az, hogy egy tetszőleges T Turing-gép utasításainak listáját egy 0-kból és 1-kből álló füzérbe kódoljuk át, ezt szalagon lehet ábrázolni. Ezt a szalagot használjuk azután valamilyen speciális U Turing-gép bevitele kezdeti részének – U-t nevezzük majd univerzális Turing-gépnek. A bevitel maradék részére U éppen úgy hat, mint ahogy T tenné. Az univerzális Turing-gép egy univerzális utánzó. A szalag kezdeti része megadja az U univerzális gépnek a teljes információt, amire annak szüksége van, hogy pontosan utánozzon bármilyen adott T gépet!
Működésének megértéséhez először szükségünk van a Turing-gépek szisztematikus megszámozására."
....
"
A Hilbert-féle probléma megoldhatatlansága
Térjünk most rá arra, amiért Turing elképzeléseit eredetileg felvetette, hogy megadja a választ Hilbert nagyon általános eldönthetőségi problémájára: létezik-e mechanikus eljárás valamilyen széles, de jól meghatározott osztályba tartozó matematikai problémák megoldására? Turing rájött, hogy a kérdést át tudja fogalmazni annak a problémának eldöntésére, hogy megáll-e vagy sem valamikor az n-edik Turing-gép, amikor az m számra hat. Erre a problémára mint megállási problémára hivatkoztak. "
...
"A matematika számára fontos lenne, hogy képesek legyünk eldönteni, mikor állnak le a Turing-gépek. Tekintsük például a következő egyenletet:
(x + 1)w + 3 + (y + 1)w + 3 = (z + 1)w + 3.
(Ha Ön a matematikai egyenleteket nem igazán kedveli, ez még ne szegje kedvét! Ezt most csak példaként mutatom, nincs szükség arra, hogy a részleteket is értse.) Ez a speciális egyenlet a matematika egyik híres megoldatlan problémájához kapcsolódik – talán mind közül a leghíresebbhez. A probléma a következő: vannak-e olyan w, x, y, z természetes számok, amelyekre a fenti egyenlet teljesül? A „Fermat utolsó tétele” (nagy Fermat-tétel) néven ismert híres állítás, amelyet a tizenhetedik századbeli kiváló francia matematikus, Pierre de Fermat (1601–1665) Diofantosz Arithmeticájának margójára írt, azt mondja, hogy az egyenlet soha nem teljesül.25 Bár foglalkozására nézve jogász (és Descartes kortársa), Fermat korának legkitűnőbb matematikusa volt. Azt állította, hogy tételére „igazán csodálatos bizonyítása” van, de a margó túl kicsi volt, így nem fért rá; azonban mind a mai napig senki nem volt képes rekonstruálni egy ilyen bizonyítást, viszont ellenpéldát sem tudtak a nagy Fermat-tételre találni!
Világos, hogy ha adott a (w, x, y, z) számnégyes, akkor csupán számolás kérdése annak eldöntése, hogy az egyenlőség fennáll-e vagy sem. Ezért el tudunk képzelni olyan számítógép-algoritmust, amely végigfut egymás után minden számnégyesen, és csak akkor áll meg, ha az egyenlet teljesül. (Láttuk, hogy vannak módok véges számsorozatok kiszámítható kódolására egyetlen szalagon, azaz egyetlen számként, így „végigfuthatunk” minden számnégyesen, követve ezen egyetlen számok természetes sorrendjét.) Ha meg tudnánk állapítani, hogy ez az algoritmus nem áll meg, akkor bizonyításunk lenne Fermat tételére."
...
Egy csodálatos elme- azt hiszem az volt a címe.
...
"Felvetődik egy természetes kérdés: hogyan döntsük el, hogy bármelyik speciális Turing-gép (meghatározott bemeneti adatokat betáplálva) megáll-e valamikor? Sok Turing-gépre ezt nem lehet nehéz megválaszolni; de a válasz, mint előbb láttuk, olykor egy komoly matematikai probléma megoldását foglalja magában. Van-e tehát valamilyen algoritmikus eljárás az általános kérdés – a megállási probléma – teljesen automatikus megválaszolására? Turing megmutatta, hogy nincs."
..."Az a kérdés, hogy egy Turing-gép megáll-e vagy sem, a matematikának egy tökéletesen jól meghatározott darabja (és már láttuk, hogy megfordítva: változatos, jelentős matematikai kérdések fogalmazhatók meg Turing-gépek megállásának problémájaként). Így megmutatva, hogy nem létezik algoritmus annak a kérdésnek eldöntésére, hogy megállnak-e a Turing-gépek, Turing bebizonyította (és ezt tette Church is saját, meglehetősen különböző megközelítésében), hogy a matematikai kérdések eldöntésére nem létezhet általános algoritmus. Hilbert eldönthetőségi problémájának nincs megoldása! "
..."Úgy tűnhet, most azt állapítottuk meg, hogy van legalább néhány eldönthetetlen matematikai kérdés. Azonban semmi ilyet nem csináltunk. Nem azt mutattuk meg, hogy van valamilyen különösen szörnyűséges Turing-gép táblázat, amelynél, valamiféle abszolút értelemben, lehetetlen eldönteni, megáll-e a gép vagy sem, amikor valamilyen különösen szörnyű számot táplálunk belé – a helyzet valójában éppen az ellenkező, amint azt egy pillanaton belül látni fogjuk. Nem mondtunk semmit egyes problémák megoldhatatlanságáról, csak problémák egyes családjainak algoritmikus megoldhatatlanságáról. A válasz bármelyik egyedi esetben vagy „igen”, vagy „nem”, így az adott eset eldöntésére bizonyára van algoritmus, nevezetesen az, amely egyszerűen „igen”-t mond, amikor feladjuk neki a problémát, vagy amelyik egyszerűen „nem”-et mond, ami szintén előfordulhat! A nehézség természetesen az, hogy nem tudhatjuk, melyik algoritmust használjuk. Ez egyetlen állítás matematikai igazsága kiderítésének, nem pedig állítások egy családja szisztematikus eldöntésének kérdése. Fontos felismerni azt, hogy az algoritmusok magukban nem döntik el a matematikai igazságot. Egy algoritmus érvényességét mindig külső eszközökkel kell megállapítani.
Hogyan győzzünk le egy algoritmust?
A matematikai állítások igazsága eldöntésének kérdésére később, Gödel tételével kapcsolatban visszatérünk (lásd a 4. fejezetet). Most rá szeretnék mutatni arra, hogy Turing érvelése valójában sokkal építőbb és kevésbé negatív, mint amilyennek eddig látszólag bemutattam. Nem mutattunk még olyan speciális Turing-gépet, amelynél, valamilyen abszolút értelemben, eldönthetetlen, hogy megáll-e vagy sem. Ha azonban gondosan megvizsgáljuk az érvelést, akkor azt találjuk, hogy eljárásunk maga hallgatólagosan már megadja a választ a látszólag „különösen szörnyűséges” gépeket illetően. Most Turing eljárását használva fogunk egy ilyet készíteni!
Church lambda-kalkulusa


A kiszámíthatóság fogalma nagyon fontos és szép matematikai elképzelés. Figyelemre méltóan új is – ahhoz képest, ahogy az ilyen alapvető dolgok mennek a matematikában –, hiszen először az 1930-as években vetették fel. Olyan elképzelés, amely végigvonul a matematika minden területén (jóllehet a legtöbb matematikus egyelőre nem nagyon izgatja magát a kiszámíthatósági kérdésekkel). Ereje részben abból a tényből táplálkozik, hogy a matematikában egyes jól meghatározott műveletek valójában nem kiszámíthatóak (ilyen egy Turing-gép megállásának eldöntése; a 4. fejezetben látunk majd egyéb példákat is). Ha ilyen nem kiszámítható dolgok nem lennének, akkor a kiszámíthatóság fogalmának nem lenne sok matematikai érdekessége. A matematikusok szeretik a rejtvényeket. Számukra érdekes rejtvény lehet annak eldöntése, hogy valamilyen matematikai művelet kiszámítható-e vagy sem. És különösen érdekes azért, mivel ennek a rejtvénynek az általános megoldása maga nem kiszámítható!
λx.[fx],
akkor ezen azt a függvényt értjük, amely mondjuk a-ra hatva az fa eredményt adja. Azaz
(λx.[fx])a = fa.
Más szavakkal λx.[fx] egyszerűen az f függvény, azaz
λx.[fx] = f.
Érdemes egy kicsit elgondolkodni. Egyike ez azoknak a matematikai szépségeknek, amelyek első ránézésre olyan szőrszálhasogatóak és maguktól értetődőek, hogy hajlamosak vagyunk a lényeget teljesen elveszteni. Vegyünk egy példát a jól ismert iskolai matematikából! Legyen az f függvény egy trigonometriai művelet, egy szög szinusza, ekkor a „sin” absztrakt függvény definíciója a következő: λx.[sin x] = sin."
Ideák.
Talán megtalálom azokat a részeket egy - amúgy általam kedvelt - blogon, ahol eléggé egyedül maradva, kilátástalanul védtem Domokos Gábort, a Gömböc szülő atyját, nemtelen komment-támadásokkal szemben, melyeket
azzal indokoltak a támadók, hogy micsoda tudománytalan dolog az, hogy Domokos saját sejtései igazolására Platon kockáit hozza fel egy komoly tudományos folyóiratban közölt cikkében.
...
"Végül 1937-ben Church és Turing egymástól függetlenül megmutatták, hogy minden kiszámítható (vagy algoritmikus) művelet – most Turing-gépek értelmében – megadható valamilyen Church-kifejezéssel (és fordítva).
...
3. Matematika és valóság...
Tor’Bled-Nam országa



Képzeljük el, hogy nagy útra indultunk egy távoli világba. Ezt a világot Tor’Bled-Namnak fogjuk hívni. Távoli detektorunk elcsípett egy jelet, amely most jelent meg az előttünk lévő képernyőn. A kép fókuszálása után ezt látjuk (3.1. ábra):
...

"Mi lehet ez a különös, változatos és csodálatosan bonyolult világ, amely utunkba került? Bizonyára sok Olvasó ismeri már, egyesek viszont még nem találkoztak vele. Ez a világ nem más, mint egy darab absztrakt matematika – a Mandelbrot nevét viselő halmaz.31 Kétségkívül nagyon bonyolult; mégis figyelemre méltóan egyszerű szabállyal képezhető! Hogy a szabályt rendesen el tudjam mondani, először azt kell elmagyaráznom, mi is egy komplex szám. Most tehát ez következik. A komplex számokra később szükségünk lesz. Abszolút alapvetőek a kvantummechanika szerkezetében, és ezért világunk működésében is, amelyben élünk. A Matematika Nagy Csodái közül is ezek alkotják az egyiket. Hogy elmagyarázzam, mi egy komplex szám, először arra kell emlékeztetnem az Olvasót, mit értünk a „valós szám” kifejezésen. Segíteni fog az is, ha utalunk e fogalom és a „való világ” realitásának kapcsolatára!"
..."Nagyon sok olyan valós szám is van azonban, amely ebben az értelemben nem kiszámítható. Az előző fejezetben láttuk, hogy vannak nem kiszámítható sorozatok, amelyek mindazonáltal tökéletesen jól meghatározottak. Vehetnénk például azt a tizedes kifejtést, amelynek π-edik jegye aszerint 0 vagy 1, hogy az n-edik Turing-gép az n számra hatva megáll-e vagy sem. A valós számoktól általában csak azt várjuk el, hogy legyen valamilyen végtelen tizedes kifejtésük. Nem várjuk, hogy legyen algoritmus az n-edik jegy előállítására, sőt még azt sem, hogy legyen tudomásunk bármilyen szabályról, amely elvileg meghatározza, hogy mi az n-edik jegy.33 A kiszámítható számokkal szörnyű dolgozni. Nem tudjuk megőrizni minden művelet kiszámíthatóságát még akkor sem, ha csak kiszámítható számokkal dolgozunk. Például még az sem kiszámítható, hogy két tetszőleges, kiszámítható számról eldöntsük, egyenlőek-e vagy sem! Ezért inkább dolgozunk az összes valós számmal, amikor a tizedes kifejtés bármilyen lehet, nem kell, hogy mondjuk egy kiszámítható sorozat legyen...
..."Nagyon sok olyan valós szám is van azonban, amely ebben az értelemben nem kiszámítható. Az előző fejezetben láttuk, hogy vannak nem kiszámítható sorozatok, amelyek mindazonáltal tökéletesen jól meghatározottak. Vehetnénk például azt a tizedes kifejtést, amelynek π-edik jegye aszerint 0 vagy 1, hogy az n-edik Turing-gép az n számra hatva megáll-e vagy sem. A valós számoktól általában csak azt várjuk el, hogy legyen valamilyen végtelen tizedes kifejtésük. Nem várjuk, hogy legyen algoritmus az n-edik jegy előállítására, sőt még azt sem, hogy legyen tudomásunk bármilyen szabályról, amely elvileg meghatározza, hogy mi az n-edik jegy.33 A kiszámítható számokkal szörnyű dolgozni. Nem tudjuk megőrizni minden művelet kiszámíthatóságát még akkor sem, ha csak kiszámítható számokkal dolgozunk. Például még az sem kiszámítható, hogy két tetszőleges, kiszámítható számról eldöntsük, egyenlőek-e vagy sem! Ezért inkább dolgozunk az összes valós számmal, amikor a tizedes kifejtés bármilyen lehet, nem kell, hogy mondjuk egy kiszámítható sorozat legyen...
Hány valós szám van?
Tartsunk egy kis szünetet, hogy méltányolhassuk az általánosítás nagyságát, melynek során a racionális számoktól eljutottunk a valósakig.
Elsőre azt gondolhatnánk, hogy már az egészek száma is nagyobb a természetes számokénál, mert minden természetes szám egész, míg egyes egészek (a negatívak) nem természetes számok; hasonlóképpen azt is gondolhatnánk, hogy a törtek száma nagyobb, mint az egészeké. Azonban ez nem így van. A végtelen számok szép és hatékony elmélete szerint, amelyet az igen eredeti orosz-német matematikus, Georg Cantor tett közzé az 1800-as évek végén, a törtek, az egészek és a természetes számok teljes száma ugyanaz az ℵ0-lal („alef null”) jelölt végtelen szám. (Érdemes megjegyezni, hogy már 250 évvel korábban, a korai 1600-as években voltak hasonló elképzelései a nagy itáliai fizikusnak és csillagásznak, Galileo Galileinek. Néhány más eredményét az 5. fejezetben felidézzük.) Hogy az egészek száma ugyanannyi, mint a természetes számoké, azt a következő „egy-egy értelmű megfeleltetésből” láthatjuk:" ...
...
.."Vegyük észre, hogy minden egész szám (a bal oldali oszlopban) és minden természetes szám (a jobb oldaliban) egyszer és csak egyszer fordul elő a táblázatban. Ez vagy az ehhez hasonló egy-egy megfeleltetés alapozza meg a Cantor-elméletben azt, hogy a bal és jobb oldali oszlopokban lévő elemek száma ugyanannyi. Az egészek száma így valóban azonos a természetes számokéval. A szám ebben az esetben végtelen, de ez nem számít. (Az egyetlen különlegesség, amely végtelen számokkal előfordul, az, hogy az egyik lista egyes tagjait elhagyhatjuk, és még így is találunk egy-egy megfeleltetést a két lista között!) Hasonló, de valamivel bonyolultabb módon egy-egy megfeleltetést állíthatunk fel a törtek és az egészek között. (Felhasználhatjuk ehhez a természetes számpárok, a számlálók és nevezők egyetlen természetes számmal való ábrázolásának egyik módját; lásd a 2. fejezetet.) A természetes számokkal egy-egy megfeleltetésbe hozható halmazokat megszámlálhatóaknak nevezzük, így a megszámlálhatóan végtelen halmazoknak van ℵ0 elemük. Most láttuk, hogy az egészek megszámlálhatóak, és ilyenek az összes törtek is."...
"Átlós eljárásunk ad tehát egy valós számot, de ez nem kiszámítható. Ezzel a gondolatmenettel ténylegesen a nem kiszámítható számok létezését lehet megmutatni. Az érvelésnek pontosan ezt a vonalát követi Turing bizonyítása, amellyel, mint ahogy az előző fejezetben elmondtuk, olyan problémák létezését mutatta meg, amelyek nem oldhatók meg algoritmikusan. A későbbiekben az átlós metszés más alkalmazásait is látni fogjuk."...
A valós számok „valóssága”


Tegyük most félre a kiszámíthatóság fogalmát. A valós számokat azért hívják „valósaknak”, mert úgy tetszik, ilyen eredményeket adnak a távolság, szög, idő, energia, hőmérséklet vagy számos egyéb geometriai és fizikai mennyiség mérései. Ám az absztrakt módon definiált „valós számok” és a fizikai mennyiségek kapcsolata nem annyira világos, mint ahogy azt képzelnénk. A valós számok inkább egy „matematikai idealizáció” eredményei, és nem valamiféle aktuális, fizikailag objektív mennyiség mérőszámai. A valós számok rendszerének megvan például az a sajátossága, hogy két tetszőlegesen közel levő között mindig van egy harmadik. Egyáltalán nem világos, hogy a fizikai távolságok vagy idők rendelkeznek-e ezzel a tulajdonsággal. Ha két pont közötti fizikai távolságot egyre tovább osztunk fel kisebb részekre, akkor végül olyan kis skálához érhetünk, amelyen maga a távolság fogalma elvesztheti a közönséges értelemben vett jelentését. Azt sejtik, hogy a „kvantumgravitáció” skáláján, egy szubatomi részecske méreténél 1020-szor kisebb távolságon34 valóban ez a helyzet. Ám hogy minden valós számot felsoroljunk, ahhoz ennél akárhányszor kisebb skálákra is el kellene mennünk: például egy részecske méreténél 10200-szor, 102000-szer vagy 1010200-szor kisebbekre. Egyáltalán nem világos, hogy van-e fizikai értelmük az ilyen abszurdul kicsi skáláknak. Hasonló megjegyzés vonatkozhat a megfelelően kicsi időtartamokra.

A fizikában a valós számok rendszerét matematikai használhatósága, egyszerűsége és eleganciája miatt választjuk, valamint azért, mert nagyon széles tartományban összhangban van a távolság és idő fizikai fogalmával. Nincs szó arról, hogy minden tartományban egyezik ezekkel a fizikai fogalmakkal. Jól látható, hogy a távolság és idő nagyon kis skáláin nincs meg ez az összhang."...
Tartsunk egy kis szünetet, hogy méltányolhassuk az általánosítás nagyságát, melynek során a racionális számoktól eljutottunk a valósakig.
Elsőre azt gondolhatnánk, hogy már az egészek száma is nagyobb a természetes számokénál, mert minden természetes szám egész, míg egyes egészek (a negatívak) nem természetes számok; hasonlóképpen azt is gondolhatnánk, hogy a törtek száma nagyobb, mint az egészeké. Azonban ez nem így van. A végtelen számok szép és hatékony elmélete szerint, amelyet az igen eredeti orosz-német matematikus, Georg Cantor tett közzé az 1800-as évek végén, a törtek, az egészek és a természetes számok teljes száma ugyanaz az ℵ0-lal („alef null”) jelölt végtelen szám. (Érdemes megjegyezni, hogy már 250 évvel korábban, a korai 1600-as években voltak hasonló elképzelései a nagy itáliai fizikusnak és csillagásznak, Galileo Galileinek. Néhány más eredményét az 5. fejezetben felidézzük.) Hogy az egészek száma ugyanannyi, mint a természetes számoké, azt a következő „egy-egy értelmű megfeleltetésből” láthatjuk:"
"Átlós eljárásunk ad tehát egy valós számot, de ez nem kiszámítható. Ezzel a gondolatmenettel ténylegesen a nem kiszámítható számok létezését lehet megmutatni. Az érvelésnek pontosan ezt a vonalát követi Turing bizonyítása, amellyel, mint ahogy az előző fejezetben elmondtuk, olyan problémák létezését mutatta meg, amelyek nem oldhatók meg algoritmikusan. A későbbiekben az átlós metszés más alkalmazásait is látni fogjuk."
"Kiderül, hogy a Természet figyelemre méltóan kegyes hozzánk, és úgy látszik, hogy ugyanazok a valós számok, amelyekhez a mindennapi vagy annál nagyobb skálájú dolgok leírásánál hozzászoktunk, hasznosságukat az atomoknál sokkal kisebb skálákon is megtartják. Biztosan lemehetünk egy szubatomi részecske, mondjuk egy elektron vagy egy proton „klasszikus” átmérőjének századánál is kisebb tartományra, és látszólag le egészen a „kvantumgravitáció skálájáig”, az előző részecskénél húsz nagyságrenddel kisebb távolságokig! Egészen rendkívüli extrapoláció ez a tapasztalattól elindulva. A valós számokkal leírható távolság megszokott fogalma érvényesnek látszik a legtávolabbi kvazárokig és azokon is túl, átfogva legalább 1042, de talán 1060 métert vagy még szélesebb tartományt. A valós számok rendszerének alkalmasságát ritkán kérdőjelezik meg. Miért ez a nagy bizalom e számok iránt a fizika pontos leírásánál, amikor használhatóságukra vonatkozó kezdeti tapasztalataink viszonylag korlátozott tartományra terjednek? Ez a – esetleg méltatlanra pazarolt – bizalom (noha ezt ritkán ismerik fel) a valós számok rendszerének logikai eleganciáján, következetességén és matematikai erején kell nyugodjék, nem feledkezve meg a Természet titkos matematikai harmóniájába vetett hitről. "...
Komplex számok


A valós számok rendszerének, mint kiderül, nincs monopóliuma a matematikai erő és elegancia területén. Sőt elég kényelmetlen, hogy négyzetgyököt csak pozitív számból (vagy nullából) lehet vonni, negatívból nem. Matematikai szempontból – és egy pillanatra félretéve minden kérdést a fizikai világgal való közvetlen kapcsolatról – rendkívül kényelmes, ha a negatív számokból ugyanúgy négyzetgyököt tudunk vonni, mint a pozitívakból. Posztuláljunk vagy „gondoljunk ki” egyszerűen egy négyzetgyököt a –1 számnak. Ezt az „i” szimbólummal fogjuk jelölni, tehát i2 = –1.
Most, hogy a –1-nek már van négyzetgyöke, nem kerül nagy erőfeszítésbe, hogy minden valós számnak megadjuk a négyzetgyökét. Ha a pozitív valós szám, akkor az
Vegyük észre, hogy amikor e mennyiségeket képeztük, megengedtük, hogy összeadjunk valós és képzetes számokat, és hogy a képzetes számokat tetszőleges valós számmal megszorozzuk (vagy nullától különböző valós számmal elosszuk, ami ugyanaz, mint a reciprokkal való szorzás). Az eredményül kapott objektumokat nevezzük komplex számoknak. Egy komplex szám a + ib
Vegyük észre, hogy amikor e mennyiségeket képeztük, megengedtük, hogy összeadjunk valós és képzetes számokat, és hogy a képzetes számokat tetszőleges valós számmal megszorozzuk (vagy nullától különböző valós számmal elosszuk, ami ugyanaz, mint a reciprokkal való szorzás). Az eredményül kapott objektumokat nevezzük komplex számoknak. Egy komplex szám a + ib

alakú, ahol a és b valós számok, a komplex számnak rendre a valós része és a képzetes része. Két ilyen szám összeadásának és összeszorzásának szabályai az (iskolai) algebra szokásos szabályait követik, kiegészítve az i2 = –1 szabállyal:
...Figyelemre méltó dolog történik most! A számoknak ezt a rendszerét azért vezettük be, hogy a négyzetgyökvonást mindig el tudjuk végezni. A célt elértük, bár még ez sem nyilvánvaló. Am ennél jóval több is teljesül: köbgyökök, ötödik gyökök, kilencvenkilencedik gyökök, π-edik gyökök, (1 + i)-edik gyökök stb. mind büntetlenül képezhetők (amint azt a nagy tizennyolcadik századbeli matematikus, Leonhard Euler képes volt megmutatni). A komplex számok mágiájának másik példájaként vizsgáljuk meg a trigonometria egyik, valamivel bonyolultabban kinéző képletét, amelyet meg kellett tanulnunk az iskolában; két szög összegének szinusza és koszinusza,sin(A + B) = sin A cos B + cos A sin B,


cos(A + B) = cos A cos B – sin A sin B,
nem más, mint rendre a képzetes és valós része a sokkal egyszerűbb (és sokkal jobban megjegyezhető!)


eA+B = eAeB


komplex egyenletnek.35 Itt mindössze az



eiA = cos A + i sin A

„Euler-formulát” kell ismernünk (a 16. századbeli jelentős angol matematikus, Roger Cotes is felállította sok évvel Euler előtt), amelyet behelyettesítünk az előző egyenletbe. Az eredmény acos(A + B) + i sin(A + B) = (cos A + i sin A)(cos B + i sin B)
kifejezés, a szorzásokat a jobb oldalon elvégezve az idézett trigonometriai összefüggéseket kapjuk.



Mi több, minden


a0 + a1z + a2z2 + a3z3 + … + anzn = 0

algebrai egyenletnek (a0, a1, a2, … , an komplex számok, an ≠ 0) van z komplex szám megoldása. Van például egy z komplex szám, amely kielégíti a

z102 + 999z33 – πz2 = –417 + i
...Figyelemre méltó dolog történik most! A számoknak ezt a rendszerét azért vezettük be, hogy a négyzetgyökvonást mindig el tudjuk végezni. A célt elértük, bár még ez sem nyilvánvaló. Am ennél jóval több is teljesül: köbgyökök, ötödik gyökök, kilencvenkilencedik gyökök, π-edik gyökök, (1 + i)-edik gyökök stb. mind büntetlenül képezhetők (amint azt a nagy tizennyolcadik századbeli matematikus, Leonhard Euler képes volt megmutatni). A komplex számok mágiájának másik példájaként vizsgáljuk meg a trigonometria egyik, valamivel bonyolultabban kinéző képletét, amelyet meg kellett tanulnunk az iskolában; két szög összegének szinusza és koszinusza,sin(A + B) = sin A cos B + cos A sin B,
nem más, mint rendre a képzetes és valós része a sokkal egyszerűbb (és sokkal jobban megjegyezhető!)
eA+B = eAeB
komplex egyenletnek.35 Itt mindössze az
eiA = cos A + i sin A
Mi több, minden
a0 + a1z + a2z2 + a3z3 + … + anzn = 0
algebrai egyenletnek (a0, a1, a2, … , an komplex számok, an ≠ 0) van z komplex szám megoldása. Van például egy z komplex szám, amely kielégíti a
z102 + 999z33 – πz2 = –417 + i
egyenletet, bár ez egyáltalán nem nyilvánvaló! Az állítást olykor az „algebra alaptételeként” idézik."...
"1831-ben a nagy matematikus és természettudós, Carl Friedrich Gauss meglepően eredeti gondolatmenettel megadta az első általános bizonyítást. Ennek kulcsfontosságú tényezője volt a komplex számok geometriai ábrázolása, és azután egy topológiai36 érvelés.


Valójában nem Gauss használta először a komplex számok geometriai leírását. "
...Bolyai és Gauss.
" A hagyományos (bár történetileg egyáltalán nem pontos) terminológiával összhangban a komplex számok szokásos geometriai ábrázolására mint Argand-síkra fogok hivatkozni.


 Az Argand-sík közönséges euklideszi sík, szabványos x és y derékszögű koordinátákkal, x a vízszintes távolságot jelöli (pozitív jobbra, negatív balra), y a függőlegeset (pozitív felfelé, negatív lefelé). A
Az Argand-sík közönséges euklideszi sík, szabványos x és y derékszögű koordinátákkal, x a vízszintes távolságot jelöli (pozitív jobbra, negatív balra), y a függőlegeset (pozitív felfelé, negatív lefelé). A z = x + iy
z = x + iy
Valójában nem Gauss használta először a komplex számok geometriai leírását. "
...

komplex számot az a pont ábrázolja az Argand-síkon, amelynek koordinátái



(x, y)


(lásd a 3.8. ábrát). Jegyezzük meg, hogy a 0-t (mint komplex számot) a koordináták kezdőpontja ábrázolja, az 1-et egy speciális pont az x tengelyen.
komplex számot az a pont ábrázolja az Argand-síkon, amelynek koordinátái
(x, y)
(lásd a 3.8. ábrát). Jegyezzük meg, hogy a 0-t (mint komplex számot) a koordináták kezdőpontja ábrázolja, az 1-et egy speciális pont az x tengelyen.
"Az Argand-sík lehetővé teszi, hogy komplex számcsaládunkat geometriailaghasznos képbe szervezzük. Ez a dolog nem igazán új számunkra. Már hozzászoktunk ahhoz, hogy a valós számokat geometriai képbe lehet rendezni, nevezetesen egy egyenes vonalra, amely mindkét irányban végtelen. A vonal egyik kiválasztott pontjára a 0, egy másikra az 1 címkét akasztjuk. A 2 pont úgy helyezkedik el, hogy távolsága az 1-től ugyanakkora, mint az 1 és a 0 távolsága; az 1/2 a középső pont 0 és 1 között; a –1 pont úgy helyezkedik el, hogy a 0 félúton legyen közötte és 1 között; stb., stb. A valós számok ily módon megjelenített halmazát valós számegyenesnek nevezzük. A komplex számoknál valójában két valós számot használunk koordinátáknak, az a + ib komplex számnál a-t és b-t. Ezek a számpárok megadják a pontok koordinátáit egy síkon – az Argand-síkon. A 3.9. ábrán példaként közelítőleg megjelöltem, hol kell elhelyezni az
u=1+i1,3; v=-2+i; w=-1,5-i0,4komplex számokat.
A komplex számok összeadásának és szorzásának alapvető algebrai műveletei most világos geometriai formát kapnak. Nézzük először az összeadást! Legyen u és v az Argand-síkon az előzőek szerint ábrázolt két komplex szám!
Ezzel ekvivalens módon azt mondhatjuk, hogy a 0, v és uv által alkotott háromszög hasonló (és hasonló állású) a 0, 1 és u által alkotott háromszöggel.
Vektoralgebra, műveletek vektorokkal.Gyuri, a legidősebb a kilenc unoka közül, mindannyiunk által elismert és elfogadott "primus inter pares"-ünk boldog izgalommal és lekesedéssel mutatja - egyetemi jegyzetekhez hasonlító,puritán kinézetű matematika könyveit, talán a téli szünetben. Ő másodikos én elsős. Ő matematika tagozatos osztályba jár Debrecenben. Az az ország egyik legjobb gimnáziuma volt akkor, és valószínűleg az most is. Ámultan hallgatom és nézem, hogy mikről tanulnak. Biztosan a komplex számokat is mutogatja, amelyekről mi még az egyetemen sem tanultunk, vagy ha igen, inkább csak "lábjegyzetként". Igazából Penrosenek ez a könyve hozta el számomra felfogható távolságra a komplex számokat. Itt és most, ahogy olvasom....
komplex számokat.
A komplex számok összeadásának és szorzásának alapvető algebrai műveletei most világos geometriai formát kapnak. Nézzük először az összeadást! Legyen u és v az Argand-síkon az előzőek szerint ábrázolt két komplex szám!
A Mandelbrot-halmaz felépítése
Most már megnézhetjük, mi a Mandelbrot-halmaz definíciója.
Legyen z tetszőleges komplex szám. Ezt az Argand-síkon egy pont ábrázolja. Tekintsük most a
z → z2 + c leképezést, amely z-t egy új komplex számmal helyettesíti, c egy másik, rögzített (azaz adott) komplex szám. A z2 + c számot az Argand-síkon egy új pont ábrázolja. Ha például c az 1,63 – i 4,2 szám, akkor a leképezés z → z2 + 1,63 – i 4,2, így például 3 a 32 + 1,63 – i 4,2 = 9 + 1,63 – i 4,2 = 10,63 – i 4,2 számmal, –2,7 + i 0,3 a (–2,7 + i 0,3)2 + 1,63 – i 4,2 = (–2,7)2 – (0,3)2 + 1,63 + i{2(–2,7)(0,3) – 4,2} = 8,83 – i 5,82 számmal helyettesítendő. Amikor a számok bonyolultak, akkor a számítást legjobb elektronikus számítógéppel végezni.Na már most, bármi is c, a 0 szám ebben a leképezésben az adott c számba megy át. És mi történik c-vel? Ezt a c2 + c számmal kell helyettesíteni. Folytassuk a sort, és alkalmazzuk a helyettesítést a c2 + c számra; a következőt kapjuk: (c2 + c)2 + c = c4 + 2c3 + c2 + c. Iteráljuk a leképezést még egyszer, alkalmazzuk most a fenti számra, (c4 + 2c3 + c2 + c)2 + c = c8 + 4c7 + 6c6 + 6c5 + 5c4 + 2c3 + c2 + c, azután újra erre a számra stb. A komplex számok egy 0-val induló sorozatát kapjuk: 0, c, c2 + c, c4 + 2c3 + c2 + c, … . Ha most az adott c komplex számot megfelelően választjuk, akkor az így kapott számsorozat soha nem vándorol túl messze az Argand-síkon a kezdőponttól; pontosabban megfogalmazva: c ilyen megválasztása esetén a sorozat korlátos marad, azaz minden tagja egy kezdőpont körüli rögzített körben fekszik (lásd 3.12. ábra). "A Mandelbrot-halmaz, azaz Tor’Bled-Nam világának fekete tartománya az Argand-síknak pontosan az a tartománya, amelyben lévő c pontokra a sorozat korlátos marad. A fehér tartomány azokat a c pontokat tartalmazza, amelyekre a sorozat nem korlátos. A korábban látott részletes képeket számítógépek kivitt adataiból rajzolták. A számítógép módszeresen végigfut a c komplex szám lehetséges értékein, mindegyikre kiszámítja a 0, c, c2 + c, … sorozatot, és alkalmas kritériumok alapján eldönti, hogy a sorozat korlátos marad-e vagy sem. Ha igen, akkor a számítógép intézkedik, hogy a képernyőre a c-nek megfelelő pontba fekete pötty kerüljön. Ha nem korlátos, akkor a számítógép fehér pontot rak ki. Végül is a vizsgált tartomány összes pontjáról eldönti, hogy azt fehérre vagy feketére színezze.
Most már megnézhetjük, mi a Mandelbrot-halmaz definíciója.
Legyen z tetszőleges komplex szám. Ezt az Argand-síkon egy pont ábrázolja. Tekintsük most a
A matematikai fogalmak platóni valósága?
A Mandelbrot-halmaz bonyolultsága igen figyelemreméltó, különösen annak tükrében, hogy e halmaz definíciója a matematikai definíciókhoz képest meglepően egyszerű. Az is igaz, hogy e halmaz általános szerkezete nem nagyon érzékeny a választott z → z2 + c leképezés pontos algebrai alakjára. Sok más iterált komplex leképezés (például z →z3 + iz2 + c) rendkívül hasonló szerkezeteket ad (feltéve, hogy az induláshoz megfelelő számot választunk – esetleg nem 0-t, hanem olyan számot, amelynek értékét világos matematikai szabály adja meg minden megfelelően választott leképezésre). Van ezeknek a „Mandelbrot”-szerkezeteknek egyfajta, az iterált komplex leképezésekkel összefüggő, univerzális vagy abszolút jellegük. Az ilyen szerkezetek tanulmányozása a matematikán belül önmagában érdekes, komplex dinamikai rendszerekként szoktak hivatkozni rájuk."
Mennyire „valóságosak” a matematikusok világának objektumai? Az egyik nézőpontból úgy látszik, hogy egyáltalán nem beszélhetünk valóságról velük kapcsolatban. A matematikai objektumok csupán fogalmak; agyszülemények, amelyeket a matematikusok csinálnak, gyakran ugyan a körülöttünk lévő világ külső megjelenése és látszólagos rendje által ösztönözve, de mégis csak szellemi idealizációk. Lehetnek-e mások, mint csupán az emberi értelem önkényes építményei? Ugyanakkor gyakran mély valóság látszik e matematikai fogalmak körül, amely messze túlmegy bármelyik matematikus szellemi termékein. Mintha valami az emberi gondolkodást örök külső igazságok felé vezetné, amelyeknek megvan a saját valóságuk, és amelyeket csak részlegesen ismer fel bármelyikünk.
4. Igazság, bizonyítás, meglátás
Hilbert programja a matematikában
Hogy a kérdést egyszerűsítsük, tekintsük csupán a matematikai igazságot. Hogyan alakítjuk ki ítéleteinket – talán még „bizonyos” tudásunkat is – a matematikai kérdésekben? Itt legalább sokkal világosabbak a dolgok. Nem lehet kérdéses, hogy az adott esetben mi igaz, és mi hamis – vagy mégis? Mi valójában a matematikai igazság?
A matematikai igazság kérdése nagyon messzire nyúlik vissza, a korai görög filozófusok és matematikusok idejére és még régebbre. Egyes nagyon nagy tisztába tételek és meglepő új meglátások azonban nagyjából az elmúlt száz év eredményei. Ezeket az új fejleményeket próbáljuk megérteni. A problémák egészen alapvetőek, és azt a kérdést érintik, hogy vajon gondolkodási folyamatunk valóban lehet-e teljesen algoritmikus természetű. Fontos, hogy ezekkel tisztába jöjjünk.
A 19. század vége felé a matematika nagy lépéseket tett előre, részben azért, mert a matematikai bizonyításnak egyre több és több hatásos módszere fejlődött ki. (David Hilbert és Georg Cantor, akikkel korábban már találkoztunk, és a kiváló francia matematikus, Henri Poincaré, akivel később fogunk megismerkedni, ők hárman voltak e fejlődés élharcosai.) A matematikusok biztonságot szereztek e hatékony módszerek használatában. Sok ilyen módszer használta a végtelen számú tagot tartalmazó halmaz40 fogalmát, és a bizonyítások gyakran éppen azért voltak sikeresek, mert a halmazokat valódi „dolgoknak” – teljes, létező egészeknek – tudták tekinteni, nem csupán potenciális lehetőségeknek.
Ez a magabiztosság azonban megtört, amikor 1902-ben a brit logista és filozófus, Bertrand Russell előállt ma már híres paradoxonjával (amelyet már Cantor is előre látott, lévén közvetlen leszármazottja az ő „átlós metszés” eljárásának).
Na már most, mi a Russell-paradoxon? Az egy R halmazra vonatkozik, amelynek definíciója a következő: R a halmaza minden halmaznak, amely nem eleme saját magának. R így halmazok bizonyos gyűjteménye; annak feltétele, hogy egy X halmaz a gyűjteményhez tartozzék, az, hogy ő maga ne legyen saját elemei között.Abszurd feltételezés-e az, hogy egy halmaz eleme saját magának? Nem igazán. Tekintsük például a végtelen (végtelen sok elemű) halmazok I halmazát. Biztos, hogy végtelen sok különböző végtelen halmaz van, így I maga végtelen. I tehát valóban hozzátartozik saját magához! Miért van akkor az, hogy Russell elgondolása paradoxonhoz vezet? Azt kérdezzük: Russell R halmaza eleme-e saját magának vagy sem? Ha nem, akkor R-hez kell tartozzon, mert R pontosan azokat a halmazokat tartalmazza, amelyek nem elemei saját maguknak. Ezért R végül is R-hez tartozik – ami ellentmondás. Ha viszont R eleme saját magának, akkor mivel „saját maga” valójában R, ezért olyan halmazhoz tartozik, amelynek elemeire az jellemző, hogy nem elemei saját maguknak, azaz végül is R nem eleme saját magának – ami megint ellentmondás!42Ez a gondolatmenet nem volt komolytalan. Russel csupán ugyanazt a típusú, nagyon általános, matematikai halmazelméleti okfejtést használta nagyon szélsőséges formában, mint amelyet a matematikusok kezdtek bizonyításaikban alkalmazni. A dolgok nyilvánvalóan kicsúsztak a matematikusok kezeiből, és sürgetővé vált, hogy sokkal pontosabban fogalmazzák meg, milyen típusú okfejtés megengedett, és milyen nem. Az feltétlenül szükséges, hogy a megengedett gondolatmenetben ne legyen ellentmondás, és hogy csak igaz állításokat engedjen meg levezetni előzőleg igaznak ismert állításokból.Russell munkatársával, Alfred North Whiteheaddel nekilátott, hogy kidolgozza axiómáknak és eljárási szabályoknak egy nagymértékben formális matematikai rendszerét.A szabályokat gondosan válogatták, hogy megakadályozzák a paradoxon jellegű gondolatmeneteket, amilyen a Russell-paradoxonhoz is vezetett. A Russell és Whitehead által készített különleges rendszer nagyszabású munka volt. Ám sok fáradsággal járt, és eléggé korlátozta a megengedett matematikai okfejtések típusait. David Hilbert, a nagy német matematikus, akivel először a 2. fejezetben találkoztunk, belekezdett egy sokkal jobban használható és átfogóbb rendszerbe. Minden korrekt matematikai típusú gondolatmenetet be kívánt illeszteni a matematika minden területéről. Mi több, Hilbert arra törekedett, hogy bizonyítani lehessen, hogy a rendszer ellentmondásmentes. Így a matematika egyszer s mindenkorra megtámadhatatlan alapzatra kerülne.Hilbertnek és követőinek reményei azonban semmivé váltak, amikor 1931-ben a 25 éves ragyogó osztrák matematikai logista, Kurt Gödel egy olyan meglepő tétellel állt elő, amely hatásosan rombolta le Hilbert programját. Gödel azt mutatta meg, hogy axiómáknak és eljárási szabályoknak tetszőleges ilyen pontos („formális”) matematikai rendszere, feltéve hogy elég széles, hogy tartalmazza egyszerű aritmetikai propozíciók (állítások) leírásait (mint a 2. fejezetben tárgyalt „Fermat utolsó tétele”), és feltéve hogy ellentmondásmentes, kell tartalmazzon olyan állítást, amely a rendszeren belül megengedett módokon nem bizonyítható és nem cáfolható. Az ilyen állítások igazsága tehát a jóváhagyott eljárásokkal „nem dönthető el”. Gödel ténylegesen meg tudta mutatni, hogy magának az axiómarendszer következetességének állítása, átalakítva megfelelő aritmetikai állítássá, szintén ilyen „eldönthetetlen” állítás. Fontos, hogy megértsük ezen „eldönthetetlenség” természetét. Látni fogjuk, miért hatolt le Gödel bizonyítása egészen a magjáig Hilbert programjának. Látni fogjuk azt is, hogyan tesz képessé Gödel tétele a meglátás felhasználásával arra, hogy túllépjünk bármely speciális formális matematikai rendszer korlátain. Ennek megértése döntő lesz sok elkövetkező fejtegetésünk szempontjából.
Hogy a kérdést egyszerűsítsük, tekintsük csupán a matematikai igazságot. Hogyan alakítjuk ki ítéleteinket – talán még „bizonyos” tudásunkat is – a matematikai kérdésekben? Itt legalább sokkal világosabbak a dolgok. Nem lehet kérdéses, hogy az adott esetben mi igaz, és mi hamis – vagy mégis? Mi valójában a matematikai igazság?
A matematikai igazság kérdése nagyon messzire nyúlik vissza, a korai görög filozófusok és matematikusok idejére és még régebbre. Egyes nagyon nagy tisztába tételek és meglepő új meglátások azonban nagyjából az elmúlt száz év eredményei. Ezeket az új fejleményeket próbáljuk megérteni. A problémák egészen alapvetőek, és azt a kérdést érintik, hogy vajon gondolkodási folyamatunk valóban lehet-e teljesen algoritmikus természetű. Fontos, hogy ezekkel tisztába jöjjünk.
Formális matematikai rendszerek
Gödel tétele
Megszámoztunk minden egyváltozós propozíciós függvényt, ezért a most leírtnak is kell legyen száma. Legyen ez k! Propozíciós függvényünk a listán a k-adik. Így ~ ∃ x[Πx bizonyítja Pw(w)-t] = Pk(w). Vizsgáljuk most e függvényt a speciális w = k érték mellett. Azt kapjuk, hogy ~ ∃ x[Πx bizonyítja Pk(k)-t] = Pk(k).A speciális Pk(k) propozíció egy tökéletesen jól definiált (szintaktikusan helyes) aritmetikai állítás. Van-e bizonyítása formális rendszerünkön belül? Van-e tagadásának, ~ Pk(k)-nak bizonyítása? A válasz mindkét kérdésre „nem” kell legyen. Ezt úgy láthatjuk, hogy megvizsgáljuk a Gödel-eljárás mögött húzódó jelentést. Noha Pk(k) aritmetikai propozíció, konstrukciója szerint azt állítja, ami a bal oldalon áll: „a rendszeren belül a Pk(k) propozíciónak nincs bizonyítása”. Ha axiómáinkat és eljárási szabályainkat gondosan fektettük le, és ha a számozást helyesen végeztük, akkor a rendszeren belül ennek a Pk(k)-nak nem lehet bizonyítása. Mert ha lenne, akkor Pk(k) állítás „jelentése”, nevezetesen, hogy nincs bizonyítás, hamis lenne, így Pk(k) mint aritmetikai propozíció hamis kellene legyen. Formális rendszerünk nem lehet olyan rosszul felépített, hogy megengedje hamis propozíciók bizonyítását! Ezért a helyzet az kell legyen, hogy Pk(k)-nak ténylegesen nincs bizonyítása. Azonban pontosan ez az, amit Pk(k) mondani próbál nekünk. Ezért amit Pk(k) mond, az igaz állítás kell legyen, így Pk(k), mint aritmetikai propozíció igaz kell legyen. Találtunk egy igaz propozíciót, amelynek a rendszeren belül nincs bizonyítása!Mi a helyzet tagadásával, ~Pk(k)-val? Az előbbiekből következik, hogy ennek sem lehet bizonyítása. Épp most állapítottuk meg, hogy ~Pk(k) hamis kell legyen (mert Pk(k) igaz), és hamis propozíciókat a feltevés szerint a rendszeren belül nem tudunk bebizonyítani! Így sem Pk(k), sem ~ Pk(k) nem bizonyítható formális rendszerünkben. Ez Gödel tétele.
Matematikai meglátás
Vegyük észre, hogy itt most valami nagyon figyelemreméltó dolog történt. Az emberek gyakran gondolnak a Gödel-tételre negatívumként – mint amely a formális matematikai gondolkodás szükségszerű korlátait mutatja meg. Akármilyen átfogónak is gondoljuk rendszerünket, mindig lesznek propozíciók, amelyek kiszöknek a hálóból. De kell-e izgasson bennünket ez a speciális Pk(k) propozíció? A fenti gondolatmenet során megállapítottuk, hogy Pk(k) igaz állítás! Sikerült valahogy meglátnunk, hogy Pk(k) igaz, annak ellenére, hogy a rendszeren belül formálisan nem bizonyítható. A szigorú matematikai formalistáknak valóban aggódniuk kell, mert éppen a fenti gondolatmenettel állapítottuk meg, hogy a formalista „igazság”-fogalom szükségképpen nem teljes. Akármilyen (következetes) formális rendszert használunk is az aritmetikára, lesznek olyan állítások, amelyekről láthatjuk, hogy igazak, de amelyekhez az előbb leírt formalista eljárással nem tudjuk hozzárendelni az igaz igazságértéket. A szigorú formalista talán úgy próbálhatja ezt megkerülni, hogy egyáltalán nem beszél az igazság fogalmáról, hanem csak egy rögzített formális rendszeren belüli bizonyíthatóságról. Ez azonban nagyon korlátozónak látszik. E nézőpontot elfogadva még az előző Gödel-féle érvelést sem tudnánk elmondani, mert annak lényeges részei használnak meggondolásokat arról, mi igaz, és mi nem igaz.45
A meglátás, amely által arra következtettünk, hogy a Pk(k) Gödel-propozíció valóban igaz állítás az aritmetikában, általános példája annak az eljárásnak, amelyet a logisták tükrözési elvként ismernek: „tükrözve” az axiómarendszer és az eljárási szabályok értelmét, és meggyőződve arról, hogy ezekkel valóban érvényes módon juthatunk el matematikai igazságokig, képesek lehetünk e meglátást újabb igaz matematikai állításokba kódolni, amelyek magukból az axiómákból és szabályokból nem vezethetők le. Pk(k) igazságának leszármaztatása, mint előbb körvonalaztam, ilyen elvre támaszkodott. Egy másik, az eredeti Gödel-féle érvelés számára lényeges (bár az előzőekben nem megadott) tükrözési elvre támaszkodik az, ahogy új matematikai igazságokat származtatnak abból a tényből, hogy egy axiómarendszer, amelyet matematikai igazságok előállítására már érvényesnek hiszünk, ténylegesen konzisztens. A tükrözési elvek gyakran tartalmaznak végtelen halmazokra vonatkozó gondolatmeneteket, és használatuknál mindig vigyáznunk kell arra, hogy ne kerüljünk túl közel az olyan jellegű érveléshez, amely Russell-típusú paradoxonhoz vezethet. A tükrözési elvek szolgáltatják a formalista gondolkodás antitézisét. Ha óvatosak vagyunk, akkor ezek képessé tesznek arra, hogy kiszökjünk egy formális rendszer merev falai közül és új matematikai meglátásokhoz jussunk, amelyek korábban nem látszottak elérhetőnek. Matematikai irodalmunkban sok teljesen elfogadható eredmény van, amelyek bizonyításai olyan meglátásokat követelnek, amelyek távol esnek az aritmetikára használatos szabványos formális rendszerek eredeti szabályaitól és axiómáitól. Mindez azt mutatja, hogy a szellemi eljárások, amelyek segítségével a matematikusok meghozzák ítéleteiket, nem egyszerűen valamely speciális formális rendszer eljárásaiban gyökereznek. Látjuk a Pk(k) Gödel-propozíció érvényességét, bár az axiómákból levezetni nem tudjuk. Az a fajta „látás”, amelyet egy tükrözési elv magában foglal, olyan matematikai meglátást követel, amely nem eredménye tisztán algoritmikus műveleteknek, amelyeket egy formális matematikai rendszerbe lehetne kódolni. Erre a 10. fejezetben majd visszatérünk.Az Olvasó észrevehet bizonyos hasonlóságot a Pk(k) igazságát, mégis „bizonyíthatatlanságát” megalapozó érvelés és a Russell-paradoxon gondolatmenete között. Van hasonlóság Turing bizonyításával is, amely megállapítja, hogy nem létezik olyan Turing-gép, amely megoldja a megállási problémát. E hasonlóságok nem véletlenek. A három között erős történeti szál teremt kapcsolatot. Turing Gödel munkájának tanulmányozása után találta meg bizonyítását. Gödel jól ismerte a Russell-paradoxont, és képes volt az ilyen paradox gondolatmenetet érvényes matematikai bizonyítássá alakítani. (Mindezek a gondolatmenetek Cantornak az előző fejezetben leírt „átlós metszés”-éből származnak.)
Miért fogadjuk el Gödel és Turing bizonyításait, noha a Russell-paradoxonhoz vezető gondolatmenetet el kellett vetnünk? Az előbbiek sokkal világosabbak és mint matematikai bizonyítások kifogástalanok, míg a Russell-paradoxon ködösebb, „óriási” halmazokkal operáló érvelésre támaszkodik. Ám el kell ismernünk, hogy a különbségek nem annyira tiszták, mint amennyire szeretnénk. A különbségek világossá tételének szándéka komoly hajtóereje volt a formalizmus egész elképzelésének. Gödel bizonyítása azt mutatja, hogy a szigorú formalista nézőpont nem tartható igazán; mégsem kínál egészében megbízható, alternatív nézőpontot. A kérdés szerintem nem megoldott. A matematikában jelenleg elfogadott eljárás48 az olyan típusú „óriási” halmazokat használó érvelés elkerülésére, mint amilyen a Russell-paradoxonhoz vezet, nem teljesen kielégítő.
Mi több, határozottan formalista módon igyekeznek megfogalmazni – vagy másképpen olyan formában, amely nem győz meg teljesen arról, hogy nem fordulhatnak elő ellentmondások.Akármi is a helyzet, én úgy látom, hogy a Gödel-féle bizonyításnak világos következménye az, hogy a matematikai igazság fogalma nem zárható be formális sémába, az túlmegy a puszta formalizmuson. Ez talán még a Gödel-tétel nélkül is világos. Mert hogyan döntjük el, mely axiómákat és eljárási szabályokat fogadjuk el, amikor egy formális rendszert próbálunk felállítani?
Döntésünkben mindig intuitív megértésünk kell vezessen, mi az, ami „magától értetődően igaz”, ha ismerjük a rendszer szimbólumainak „értelmét”. Hogyan döntjük el, milyen formális rendszereket ésszerű elfogadni – összhangban intuitív érzéseinkkel a „magától értetődő”-ről és „értelem”-ről – és milyeneket nem? Az önkonzisztencia követelménye erre bizonyára nem megfelelő. Sok önkonzisztens rendszer lehet ebben az értelemben nem „ésszerű”, ezeknél az axiómák és eljárási szabályok olyan állítások, amelyeket mint hamisakat vagy esetleg értelmetleneket elvetünk. „Magától értetődő” és „értelem” olyan fogalmak, amelyekre még a Gödel-tétel nélkül is szükség volna.A Gödel-tétel nélkül azonban elképzelhetnénk, hogy a „magától értetődő” és „értelem” intuitív fogalmait csupán a formális rendszer felállításánál alkalmazzuk, utána, az igazság meghatározására szolgáló tiszta matematikai érvelésben eltekintünk tőlük. Ekkor, a formalista nézettel összhangban, ezek a „homályos” intuitív fogalmak a matematikus előzetes gondolkodásának részeként jutnának szerephez, útmutatóként az alkalmas formális érvelés megtalálásához; de nem játszanának szerepet a matematikai igazság tényleges bemutatásában.
Gödel tétele azt mutatja, hogy ez a nézőpont egy matematikai alapfilozófiában nem igazán tartható. A matematikai igazság fogalma túlmegy a formalizmus egész koncepcióján. Van benne valami abszolút és „istenadta”. Ez az, amiről az előző fejezet végén tárgyalt matematikai platonizmusban szó van. Bármilyen speciális formális rendszer ideiglenes és „ember alkotta” minőséget fejez ki róla. E rendszerek valóban nagyon értékes szerepet játszanak a matematikai vizsgálatokban, de az igazsághoz csak részleges (vagy közelítő) útmutatással szolgálhatnak. Az igazi matematikai igazság túlmegy a csupán ember alkotta konstrukciókon.
Vannak olyan elképzelések is, hogy igazából az univerzum nem más, mint egy matematikai struktúra. Max Tegmark Our Mathematical Universe című könyvében foglalkozik ezzel a gondolattal.
Tény, hogy a matematika valamiért, valahogy a természet lényege. Hogy ez miért lehet így, hogy valamilyen vélt vagy valós konklúzióra juthassunk, kövessük Wigner Jenő gondolatmenetét.
A matematika a mennyiségekből a műveletek által létrehozott csoportokból és tulajdonságokból struktúrákat hoz létre és ezen struktúrák tulajdonságait vizsgálja.
Ez a meghatározás a geometriára is érvényes, hiszen a geometriát is kezelhetjük mennyiségeken és műveleteken keresztül.
Mi a fizika (és gyakorlatilag valamennyi természettudomány)?
A fizika a valóság, a létező világ, a természet leírása. A fizikán keresztül ismerjük meg a valóság alkotó elemeit, tulajdonságait, egymással való kapcsolatát, kölcsönhatásait. A fizika leírja a való világot, tényeket állapít meg a létező dolgokról, megfigyeli a tulajdonságait. Keresi, meghatározza és leírja a való világ építő elemeit, hogyan hatnak egymásra, hogyan kapcsolódnak egymáshoz, hogyan építenek a kölcsönhatások által struktúrákat.
A fizika alapvetően a valósággal foglalkozik, de a fizikát kiterjeszthetjük a nem tapasztalt valóságra is. Például a fizika foglalkozhat a multiverzummal is, de ebben az esetben is a cél a valóság megismerése. A multiverzumot is azért találjuk ki, mert úgy gondoljuk, hogy az a valóság része.
A fizika foglalkozhat alternatív valósággal is, de ebben az esetben is a fizika a megvalósulható valóságot keresi, a fizika feltételezi, hogy ezek az alternatív valóságok létezhetnek.
Fontos tulajdonsága a valóságnak, hogy a kölcsönhatások által létrejött struktúráknak új, a felépítő elemek által nem hordozott tulajdonságai jöhetnek létre.
Előzőleg megállapítja, hogy ugyanez áll a matematikai struktúrák kölcsönhatására is.A matematika absztrakt, a fizika konkrét tudományA fizika konkrét tudomány, mindig valamilyen létező minőségre, dologra vonatkozik. A fizika nem elvonatkoztatható attól a valóságtól, amit tárgyal.
A matematika univerzális, a fizika specifikus tudomány
Mivel a matematika nem kötődik a dolgok minőségéhez, nem is függ tőle. A matematika bármilyen anyagi minőségen alkalmazható. Természetesen nem minden matematikai művelet értelmezhető és ezért nem minden matematikai művelet használható különböző anyagi minőségekre, de ez nem a matematika korlátja, hanem az anyagi világunk jellemzője.
A matematika tisztán teoretikus tudomány, a fizika alapja a megfigyelés.Mivel a matematika nem foglalkozik az anyagi minőséggel, teoretikus, az anyagi világunkat nem figyelembe vevő módon kezelhető, formázható, fejleszthető. A működésének szabálya és korlátja az alapvető logika, a nyilvánvaló igazságok. Mivel a matematikát a valóság nem korlátozza, nem ellentmondásmentes tudomány (Göddel felismerés).A fizika alapja és korlátja a megfigyelés, a létező világ. A fizika fejleszthető teoretikusan, akár csupán a matematika eszközeivel is - ilyenkor szoktunk rácsodálkozni a matematika szerepére a természetben -, mégis a legszebb teória, a leglogikusabb következtetés is bizonyulhat hibásnak a fizikában - ahogy az meg is történik sokszor - ha nem felel meg a valóságnak.
A matematika nem minden értelmezhető művelete értelmezhető művelete a valóságnak is. A valóság ezen tulajdonsága biztosítja egyben azt is, hogy a valóság ellentmondás mentes rendszert alkosson. Ha egy elméleti következtetés a fizikában ellentmondásra vezet, akkor az az elméleti út bizonyosan nem lehet érvényes a valóságban.
A matematikai megismerés eszköze az elméleti következtetés, de az ellentmondás mentesség nem zárható ki.
A fizika lényegét tekintve ugyanazt a feladatot végzi, mint a matematika. Mindkettő elemek összességével foglalkozik. A matematika az elemeken matematikai műveleteket végez, a fizika létező kölcsönhatásokat vizsgál. Mindkettő a műveletekkel-kölcsönhatásokkal létrejött új struktúrák tulajdonságaival foglalkozik.
A fizika annyiban több a matematikánál, hogy a minőséggel is foglalkozik, és ugyanezért kevesebb is nála. A fizika annyiban korlátozottabb a matematikánál, hogy a valóság az összes lehetséges lehetőségeknek egy részhalmaza.
Érdekes és fontos jellemzője mindkét tudománynak, hogy mindkettő lezárhatatlan. Mindkét tudományra jellemző, hogy a műveletek-kölcsönhatások során új rendszerek keletkeznek, új tulajdonságokkal. A fizikának az elméleti korlátját a megvalósult valóság végessége határozza meg, a matematikának nincs ilyen korlátja.
Mi a matematika és a fizika kapcsolata?
A matematika a fizikai megismerés eszköze. Mivel a matematika a mennyiségekkel, a valóság minőségétől független jellemzőjével foglalkozik, a matematikai műveletek érvényesek a fizikában.
Fordítva a kijelentés nem érvényes. A fizika nem eszköze a matematika megismerésének. A valós világ korlátozza a matematika érvényességet. Egy valós anyagi rendszerre nem minden matematikai művelet értelmes vagy értelmezhető. A fizika, a valóság korlátozza, hogy melyek azok a matematikai műveletek, amelyek érvényesek az adott anyagi rendszerre.
Alapvető tulajdonsága a fizikának, hogy azok a matematikai műveletek, amelyek az adott fizikai rendszerre érvényesek, univerzálisan érvényesek. Helytől, időtől, és egyéb körülményektől függetlenül működnek. Ezek a fizikai valóságunk szimmetriái. Ezen szimmetriák azért létezhetnek, mert az adott fizikai kölcsönhatások matematikai leírásában szimmetria létezik, érvényes.
A fizika és a matematika kapcsolata egyirányú. A fizika mindig követi a matematika (aktuálisan érvényes) szabályait, de a fizika, a valóság nem meghatározó korlátja a matematikának. A matematika korlátja a tiszta logika (ha egy bizonyítás lépései igazak, akkor a bizonyítás következménye, eredménye is igaz), kiinduló szabályai a nyilvánvaló, vagy absztrakt igazságok (például, ha két mennyiség különböző, akkor azok nem egyformák, vagy ha két egyenes nem találkozik, akkor nincs közös pontjuk).
A valóság megismerésében egy következtetés lépéseinek igazsága a tiszta logikán kívül (mellett, helyett) a megfigyelés pontatlan eszközeire is támaszkodik, az absztrakt igazságok pedig sokszor értelmezhetetlenek a valóságban (két alma különböző is lehet meg azonos is, és a valóságban nem létezik végtelen hosszúságú, de végtelenül vékony struktúra).
A valós világ, a fizika kölcsönhatásokra épül, a kölcsönhatások a valós világ műveletei. A kölcsönhatások szabályozzák a valós világ működését. A fizikai kölcsönhatásoknak specifikus szabályai vannak. Mivel a kölcsönhatások mennyiségeket is jelentenek, a fizikai kölcsönhatások a matematika eszközeivel leírhatok, azonban mivel a kölcsönhatások specifikusak, speciális jellemzőkkel bírnak, csak bizonyos meghatározott matematikai eszközök használhatók, érvényesek. Ezeknek a specialitásoknak a felismerése adja a fizika, mint tudomány célját, a matematika pedig eszközöket biztosít ennek a megismerésnek.
Miért működik a matematika a valóság megismerésében?
Mivel a valóság mennyiségekre épül, a matematika természetszerűleg alkalmazható a világ megismerésében. A valóságban megvalósuló, létező kölcsönhatásoknak a fizikai mennyiségekre vonatkozó specifikuma szabályozza, határozza meg, hogy mely matematikai műveletek alkalmazhatók az adott anyagi rendszerre. Például, a quantum mechanikában szükséges az irracionális számok használata. Miért? Azért, mert a quantum mechanika kölcsönhatásainak rendszere, struktúrája, szimmetriai megfeleltethető az irracionális számok műveleteinek, a matematikai eszközrendszer struktúrájának. A fizika más területein is hasonló megfeleltetések érvényesek.
A fizika fejlődése a megfigyelésen alapszik. Azonban, ha már képesek vagyunk egy közelítő képet alkotni az adott fizikai rendszerről és a kölcsönhatásairól, a fizika fejlődhet teoretikusan is, a logika eszközei segítségével, de minden új következtetés csak akkor tekinthető érvényesnek, ha a valóság, a megfigyelés támogatja, megfelel a következtetésnek.
A matematika mitől a nyelve a fizikának?
Ha a matematika ennyire idealizált és ennyire valóságtól független, hogyan lehet mégis ennyire alapvető, érvényes és meghatározó a fizikában?
Minden, ami eddig megállapításra került a matematikával és a fizikával kapcsolatban, igazolja a matematikának a szoros kapcsolatát a fizikával. Azonban minden eddigi megállapítás, bár lényegi dolog, nem mutat rá az alapvető kapcsolatra. Az alapvető kérdés továbbra is fennáll. Az egy meg egy miért kettő a fizikában is? Az egy meg egy miért mindig kettő mindenhol az univerzumban? A matematika mitől nyelve a fizikának? A valóság miért követi a matematika szabályait? Miért használhatók a fizikai mennyiségekre a matematika műveletei és szabályai?
Látszólag van kivétel ez alól a szabály alól. Látszólag lehet találni kivételt a természeti törvényekben, ahol nem érvényes a logikára épülő matematika. Például a sebességek össze adásában. Tudjuk, a speciális relativitáselmélet megmutatta, a valóság pedig igazolta, hogy az, ami az alapvető logika szabályai szerint érvényesnek kellene lennie, a sebességek egyszerű összeadása nem valós művelete a valóságnak. Mintha a valóság nem engedelmeskedne a matematikának. Mintha lenne kivétel a matematika univerzalitása alól. Valójában ebben az esetben sem a matematika érvényessége sérül. A matematika szabályai, műveletei a sebességek összeadására is érvényes, csakhogy a valóság, a valóságunk olyan, hogy a sebességeket nem az összeadás matematikai műveletével lehet összegezni. A sebességek összegzésére egy összetettebb matematikai összefüggés érvényes, amely - hogy a mi valóságunkra specifikus legyen - tartalmaz még egy természeti állandót is. A speciális relativitás elméletének sebességek összeadására vonatkozó matematikai művelete, tehát a matematika érvényes, legalábbis addig, amíg fel nem ismerünk egy még pontosabb összefüggést. A sebességek össze adásában nem a matematika volt pontatlan, hanem a valóság nem a matematika egyszerű összeadás műveletet használja, hanem egy annál bonyolultabb matematikai formulát. A matematikai formula, az abban használt általános matematikai műveletek érvényesek.
A fizika kapcsolata a matematikával nagyon szorosnak kell lennie, hiszen a matematika, az érvényes formája korlátlanul érvényes az adott fizikában. Előfordulhat, hogy időnként át kell írni a fizika matematikai képleteit, de soha nem azért, mert a matematika elvei bizonyulnak hibásnak, hanem azért, mert kiderül, hogy a valóságról alkotott, a tapasztaláson, megfigyelésen alapuló elképzelésünk pontatlan volt. A matematika hibátlan, a valóságról alkotott képünk - amelyre alkalmaztuk a matematikát, hogy leírjuk a szabályait - pontatlan.
Az alapvető kérdés azonban még mindig fennáll. A matematika műveletei miért érvényesek korlátlanul, bárhol, bármikor a fizikai valóságban?
Ahogy az korábban megfogalmazásra került: a matematika azért létezik, azért van struktúrája, azért érvényesek a matematikai műveletek univerzálisan a matematikában, mert:
"A matematika alapját diszkrét, egymástól egyértelműen elválasztott, azonos tulajdonságú elemek alkotják. Bármilyen közel is van két nem azonos szám egymáshoz, azok különböznek egymástól, és ha két szám egyforma, akkor azok minden tulajdonságukban megegyeznek. A műveletek erre az alapra építkezve kapcsolnak össze mennyiségeket, hoznak létre új tulajdonságokat és csoportokat. A műveletek az alapot alkotó mennyiségekre egyformán vonatkoznak. Azonos műveletek azonos eljárásokat jelentenek valamennyi, az alapot alkotó mennyiségre. A matematikai struktúrákat a matematikai műveletek hozzák létre. A struktúrákat a műveletekkel egymáshoz kapcsolt mennyiségek azonos tulajdonságú csoportjai, a létrejövő struktúrák tulajdonságai, ezek egymással kapcsolatban álló viszonyai alkotják."
A matematika azért tudomány, azért működhet, a matematikai műveletek azért érvényesek a matematikán belül univerzálisan, mert a matematika alapját diszkrét, egymástól egyértelműen elválasztott, azonos tulajdonságú elemek alkotják. A fizikai kölcsönhatások megfeleltethetők a matematikai műveleteknek. Tehát abban a valóságban, amelyet diszkrét, egymástól egyértelműen elválasztott, azonos tulajdonságú elemek alkotnak, abban a valóságban, amely ezen alapra épül fel érvényesülhetnek a matematika műveletei. A valóságnak ilyennek kell lennie.
A matematika érvényességének következménye - konklúzió
Mivel a matematika műveletei helytől függetlenül mindenhol működnek a fizikai valóságban, a fizikai valóságunk minden helyszínére igaznak kell lennie ennek az állításnak, hogy a fizikai valóságukat egymástól egyértelműen elválasztott, azonos tulajdonságú elemek alkotják. Az üres térre is. Ahhoz, hogy a matematika általánosan érvényes legyen a fizikai valóságra, az üres tér alapjának is a diszkrét, egymástól egyértelműen elválasztott, azonos tulajdonságú elemeknek kell lennie.
A matematika a nullához végtelenül közeli és egymástól végtelenül kis távolságra lévő mennyiségekkel is tud dolgozni. Ezért is univerzális a matematika. A természet valószínűleg nem ilyen. A valóság nem kedveli a végtelent. A valóságunknak valószínűleg van legkisebb egysége és valószínűleg léteznie kell a legkisebb távolságnak is az egységek között. Ezen korlátok felett a matematika műveletei érvényesülnek az így felépült fizikai valóságban.
A logikát követve, a világunknak - ahol a matematika érvényes - ilyennek kell lennie. De vajon ilyen-e a világunk? A tapasztalat, a megfigyelés támogatja-e ezt a logikai következtetést? A legkisebbel foglalkozó tudomány, a kvantummechanika nem mond ellent ennek. A kvantummechanika már felismerte a legkisebb mennyiséget, ami a Planck állandóhoz köthető és a kvantummechanikában az üres tér sem üres, hanem egy mindenütt jelenlévő kvantumhabként viselkedik.
A legkisebb valóságról alkotott képünk nem mond ellent a matematika és a fizika kapcsolatáról alkotott elméleti következtetésnek. A relativitáselmélet, a nagy mennyiségekkel foglalkozó tudomány azonban kizárta az éter jelenlétét. Az igazság inkább az, hogy a relativitáselmélet nem kizárja az éter létezését, hanem nem látja az éter jelenlétét és nincs szüksége az éter létezésére.
A matematika általános érvényessége azonban sugallja, hogy egy alapstruktúra létezhet a természetben. Az éter, mint alap struktúra létezhet a fizikai valóságban is, csak nem úgy, ahogy azt a relativitás elmélete eredetileg feltételezi.
A GondolHAT következtetése szerint a matematikának ahhoz, hogy általánosan érvényes legyen a maga képére kell alakítania a valóságot és ehhez megteremtenie illetve feltételeznie az üres tér helyett az étert, mint fizikai létezőt. Akkor most melyik tudomány is írja le a valóságot? Mégis a matematika?
A matematika nem természettudomány. Kezdtem kékkel a Penrose könyvének
A matematika a mennyiségekből a műveletek által létrehozott csoportokból és tulajdonságokból struktúrákat hoz létre és ezen struktúrák tulajdonságait vizsgálja.
Ez a meghatározás a geometriára is érvényes, hiszen a geometriát is kezelhetjük mennyiségeken és műveleteken keresztül.
Mi a fizika (és gyakorlatilag valamennyi természettudomány)?
A fizika a valóság, a létező világ, a természet leírása. A fizikán keresztül ismerjük meg a valóság alkotó elemeit, tulajdonságait, egymással való kapcsolatát, kölcsönhatásait. A fizika leírja a való világot, tényeket állapít meg a létező dolgokról, megfigyeli a tulajdonságait. Keresi, meghatározza és leírja a való világ építő elemeit, hogyan hatnak egymásra, hogyan kapcsolódnak egymáshoz, hogyan építenek a kölcsönhatások által struktúrákat.
A fizika alapvetően a valósággal foglalkozik, de a fizikát kiterjeszthetjük a nem tapasztalt valóságra is. Például a fizika foglalkozhat a multiverzummal is, de ebben az esetben is a cél a valóság megismerése. A multiverzumot is azért találjuk ki, mert úgy gondoljuk, hogy az a valóság része.
A fizika foglalkozhat alternatív valósággal is, de ebben az esetben is a fizika a megvalósulható valóságot keresi, a fizika feltételezi, hogy ezek az alternatív valóságok létezhetnek.
Fontos tulajdonsága a valóságnak, hogy a kölcsönhatások által létrejött struktúráknak új, a felépítő elemek által nem hordozott tulajdonságai jöhetnek létre.
A fizika konkrét tudomány, mindig valamilyen létező minőségre, dologra vonatkozik. A fizika nem elvonatkoztatható attól a valóságtól, amit tárgyal.
A matematika univerzális, a fizika specifikus tudomány
Mivel a matematika nem kötődik a dolgok minőségéhez, nem is függ tőle. A matematika bármilyen anyagi minőségen alkalmazható. Természetesen nem minden matematikai művelet értelmezhető és ezért nem minden matematikai művelet használható különböző anyagi minőségekre, de ez nem a matematika korlátja, hanem az anyagi világunk jellemzője.
A fizika alapja és korlátja a megfigyelés, a létező világ. A fizika fejleszthető teoretikusan, akár csupán a matematika eszközeivel is - ilyenkor szoktunk rácsodálkozni a matematika szerepére a természetben -, mégis a legszebb teória, a leglogikusabb következtetés is bizonyulhat hibásnak a fizikában - ahogy az meg is történik sokszor - ha nem felel meg a valóságnak.
A matematika nem minden értelmezhető művelete értelmezhető művelete a valóságnak is. A valóság ezen tulajdonsága biztosítja egyben azt is, hogy a valóság ellentmondás mentes rendszert alkosson. Ha egy elméleti következtetés a fizikában ellentmondásra vezet, akkor az az elméleti út bizonyosan nem lehet érvényes a valóságban.
A matematikai megismerés eszköze az elméleti következtetés, de az ellentmondás mentesség nem zárható ki.
A fizika lényegét tekintve ugyanazt a feladatot végzi, mint a matematika. Mindkettő elemek összességével foglalkozik. A matematika az elemeken matematikai műveleteket végez, a fizika létező kölcsönhatásokat vizsgál. Mindkettő a műveletekkel-kölcsönhatásokkal létrejött új struktúrák tulajdonságaival foglalkozik.
A fizika annyiban több a matematikánál, hogy a minőséggel is foglalkozik, és ugyanezért kevesebb is nála. A fizika annyiban korlátozottabb a matematikánál, hogy a valóság az összes lehetséges lehetőségeknek egy részhalmaza.
Érdekes és fontos jellemzője mindkét tudománynak, hogy mindkettő lezárhatatlan. Mindkét tudományra jellemző, hogy a műveletek-kölcsönhatások során új rendszerek keletkeznek, új tulajdonságokkal. A fizikának az elméleti korlátját a megvalósult valóság végessége határozza meg, a matematikának nincs ilyen korlátja.
Mi a matematika és a fizika kapcsolata?
A matematika a fizikai megismerés eszköze. Mivel a matematika a mennyiségekkel, a valóság minőségétől független jellemzőjével foglalkozik, a matematikai műveletek érvényesek a fizikában.
Fordítva a kijelentés nem érvényes. A fizika nem eszköze a matematika megismerésének. A valós világ korlátozza a matematika érvényességet. Egy valós anyagi rendszerre nem minden matematikai művelet értelmes vagy értelmezhető. A fizika, a valóság korlátozza, hogy melyek azok a matematikai műveletek, amelyek érvényesek az adott anyagi rendszerre.
Alapvető tulajdonsága a fizikának, hogy azok a matematikai műveletek, amelyek az adott fizikai rendszerre érvényesek, univerzálisan érvényesek. Helytől, időtől, és egyéb körülményektől függetlenül működnek. Ezek a fizikai valóságunk szimmetriái. Ezen szimmetriák azért létezhetnek, mert az adott fizikai kölcsönhatások matematikai leírásában szimmetria létezik, érvényes.
A fizika és a matematika kapcsolata egyirányú. A fizika mindig követi a matematika (aktuálisan érvényes) szabályait, de a fizika, a valóság nem meghatározó korlátja a matematikának. A matematika korlátja a tiszta logika (ha egy bizonyítás lépései igazak, akkor a bizonyítás következménye, eredménye is igaz), kiinduló szabályai a nyilvánvaló, vagy absztrakt igazságok (például, ha két mennyiség különböző, akkor azok nem egyformák, vagy ha két egyenes nem találkozik, akkor nincs közös pontjuk).
A valóság megismerésében egy következtetés lépéseinek igazsága a tiszta logikán kívül (mellett, helyett) a megfigyelés pontatlan eszközeire is támaszkodik, az absztrakt igazságok pedig sokszor értelmezhetetlenek a valóságban (két alma különböző is lehet meg azonos is, és a valóságban nem létezik végtelen hosszúságú, de végtelenül vékony struktúra).
A valós világ, a fizika kölcsönhatásokra épül, a kölcsönhatások a valós világ műveletei. A kölcsönhatások szabályozzák a valós világ működését. A fizikai kölcsönhatásoknak specifikus szabályai vannak. Mivel a kölcsönhatások mennyiségeket is jelentenek, a fizikai kölcsönhatások a matematika eszközeivel leírhatok, azonban mivel a kölcsönhatások specifikusak, speciális jellemzőkkel bírnak, csak bizonyos meghatározott matematikai eszközök használhatók, érvényesek. Ezeknek a specialitásoknak a felismerése adja a fizika, mint tudomány célját, a matematika pedig eszközöket biztosít ennek a megismerésnek.
Miért működik a matematika a valóság megismerésében?
Mivel a valóság mennyiségekre épül, a matematika természetszerűleg alkalmazható a világ megismerésében. A valóságban megvalósuló, létező kölcsönhatásoknak a fizikai mennyiségekre vonatkozó specifikuma szabályozza, határozza meg, hogy mely matematikai műveletek alkalmazhatók az adott anyagi rendszerre. Például, a quantum mechanikában szükséges az irracionális számok használata. Miért? Azért, mert a quantum mechanika kölcsönhatásainak rendszere, struktúrája, szimmetriai megfeleltethető az irracionális számok műveleteinek, a matematikai eszközrendszer struktúrájának. A fizika más területein is hasonló megfeleltetések érvényesek.
A fizika fejlődése a megfigyelésen alapszik. Azonban, ha már képesek vagyunk egy közelítő képet alkotni az adott fizikai rendszerről és a kölcsönhatásairól, a fizika fejlődhet teoretikusan is, a logika eszközei segítségével, de minden új következtetés csak akkor tekinthető érvényesnek, ha a valóság, a megfigyelés támogatja, megfelel a következtetésnek.
A matematika mitől a nyelve a fizikának?
Ha a matematika ennyire idealizált és ennyire valóságtól független, hogyan lehet mégis ennyire alapvető, érvényes és meghatározó a fizikában?
Minden, ami eddig megállapításra került a matematikával és a fizikával kapcsolatban, igazolja a matematikának a szoros kapcsolatát a fizikával. Azonban minden eddigi megállapítás, bár lényegi dolog, nem mutat rá az alapvető kapcsolatra. Az alapvető kérdés továbbra is fennáll. Az egy meg egy miért kettő a fizikában is? Az egy meg egy miért mindig kettő mindenhol az univerzumban? A matematika mitől nyelve a fizikának? A valóság miért követi a matematika szabályait? Miért használhatók a fizikai mennyiségekre a matematika műveletei és szabályai?
Látszólag van kivétel ez alól a szabály alól. Látszólag lehet találni kivételt a természeti törvényekben, ahol nem érvényes a logikára épülő matematika. Például a sebességek össze adásában. Tudjuk, a speciális relativitáselmélet megmutatta, a valóság pedig igazolta, hogy az, ami az alapvető logika szabályai szerint érvényesnek kellene lennie, a sebességek egyszerű összeadása nem valós művelete a valóságnak. Mintha a valóság nem engedelmeskedne a matematikának. Mintha lenne kivétel a matematika univerzalitása alól. Valójában ebben az esetben sem a matematika érvényessége sérül. A matematika szabályai, műveletei a sebességek összeadására is érvényes, csakhogy a valóság, a valóságunk olyan, hogy a sebességeket nem az összeadás matematikai műveletével lehet összegezni. A sebességek összegzésére egy összetettebb matematikai összefüggés érvényes, amely - hogy a mi valóságunkra specifikus legyen - tartalmaz még egy természeti állandót is. A speciális relativitás elméletének sebességek összeadására vonatkozó matematikai művelete, tehát a matematika érvényes, legalábbis addig, amíg fel nem ismerünk egy még pontosabb összefüggést. A sebességek össze adásában nem a matematika volt pontatlan, hanem a valóság nem a matematika egyszerű összeadás műveletet használja, hanem egy annál bonyolultabb matematikai formulát. A matematikai formula, az abban használt általános matematikai műveletek érvényesek.
A fizika kapcsolata a matematikával nagyon szorosnak kell lennie, hiszen a matematika, az érvényes formája korlátlanul érvényes az adott fizikában. Előfordulhat, hogy időnként át kell írni a fizika matematikai képleteit, de soha nem azért, mert a matematika elvei bizonyulnak hibásnak, hanem azért, mert kiderül, hogy a valóságról alkotott, a tapasztaláson, megfigyelésen alapuló elképzelésünk pontatlan volt. A matematika hibátlan, a valóságról alkotott képünk - amelyre alkalmaztuk a matematikát, hogy leírjuk a szabályait - pontatlan.
Az alapvető kérdés azonban még mindig fennáll. A matematika műveletei miért érvényesek korlátlanul, bárhol, bármikor a fizikai valóságban?
Ahogy az korábban megfogalmazásra került: a matematika azért létezik, azért van struktúrája, azért érvényesek a matematikai műveletek univerzálisan a matematikában, mert:
"A matematika alapját diszkrét, egymástól egyértelműen elválasztott, azonos tulajdonságú elemek alkotják. Bármilyen közel is van két nem azonos szám egymáshoz, azok különböznek egymástól, és ha két szám egyforma, akkor azok minden tulajdonságukban megegyeznek. A műveletek erre az alapra építkezve kapcsolnak össze mennyiségeket, hoznak létre új tulajdonságokat és csoportokat. A műveletek az alapot alkotó mennyiségekre egyformán vonatkoznak. Azonos műveletek azonos eljárásokat jelentenek valamennyi, az alapot alkotó mennyiségre. A matematikai struktúrákat a matematikai műveletek hozzák létre. A struktúrákat a műveletekkel egymáshoz kapcsolt mennyiségek azonos tulajdonságú csoportjai, a létrejövő struktúrák tulajdonságai, ezek egymással kapcsolatban álló viszonyai alkotják."
A matematika azért tudomány, azért működhet, a matematikai műveletek azért érvényesek a matematikán belül univerzálisan, mert a matematika alapját diszkrét, egymástól egyértelműen elválasztott, azonos tulajdonságú elemek alkotják. A fizikai kölcsönhatások megfeleltethetők a matematikai műveleteknek. Tehát abban a valóságban, amelyet diszkrét, egymástól egyértelműen elválasztott, azonos tulajdonságú elemek alkotnak, abban a valóságban, amely ezen alapra épül fel érvényesülhetnek a matematika műveletei. A valóságnak ilyennek kell lennie.
A matematika érvényességének következménye - konklúzió
Mivel a matematika műveletei helytől függetlenül mindenhol működnek a fizikai valóságban, a fizikai valóságunk minden helyszínére igaznak kell lennie ennek az állításnak, hogy a fizikai valóságukat egymástól egyértelműen elválasztott, azonos tulajdonságú elemek alkotják. Az üres térre is. Ahhoz, hogy a matematika általánosan érvényes legyen a fizikai valóságra, az üres tér alapjának is a diszkrét, egymástól egyértelműen elválasztott, azonos tulajdonságú elemeknek kell lennie.
A matematika a nullához végtelenül közeli és egymástól végtelenül kis távolságra lévő mennyiségekkel is tud dolgozni. Ezért is univerzális a matematika. A természet valószínűleg nem ilyen. A valóság nem kedveli a végtelent. A valóságunknak valószínűleg van legkisebb egysége és valószínűleg léteznie kell a legkisebb távolságnak is az egységek között. Ezen korlátok felett a matematika műveletei érvényesülnek az így felépült fizikai valóságban.
A logikát követve, a világunknak - ahol a matematika érvényes - ilyennek kell lennie. De vajon ilyen-e a világunk? A tapasztalat, a megfigyelés támogatja-e ezt a logikai következtetést? A legkisebbel foglalkozó tudomány, a kvantummechanika nem mond ellent ennek. A kvantummechanika már felismerte a legkisebb mennyiséget, ami a Planck állandóhoz köthető és a kvantummechanikában az üres tér sem üres, hanem egy mindenütt jelenlévő kvantumhabként viselkedik.
A legkisebb valóságról alkotott képünk nem mond ellent a matematika és a fizika kapcsolatáról alkotott elméleti következtetésnek. A relativitáselmélet, a nagy mennyiségekkel foglalkozó tudomány azonban kizárta az éter jelenlétét. Az igazság inkább az, hogy a relativitáselmélet nem kizárja az éter létezését, hanem nem látja az éter jelenlétét és nincs szüksége az éter létezésére.
A matematika általános érvényessége azonban sugallja, hogy egy alapstruktúra létezhet a természetben. Az éter, mint alap struktúra létezhet a fizikai valóságban is, csak nem úgy, ahogy azt a relativitás elmélete eredetileg feltételezi.
A GondolHAT következtetése szerint a matematikának ahhoz, hogy általánosan érvényes legyen a maga képére kell alakítania a valóságot és ehhez megteremtenie illetve feltételeznie az üres tér helyett az étert, mint fizikai létezőt. Akkor most melyik tudomány is írja le a valóságot? Mégis a matematika?
A matematika nem természettudomány. Kezdtem kékkel a Penrose könyvének
Matematikai meglátás
Platonizmus vagy intuicionizmus?
Gödel-típusú tételek Turing eredményéből
Így ha Hilbertnek sikerült volna megtalálnia matematikai rendszerét – axiómák és eljárási szabályok egy rendszerét, amely elég erős, hogy formális bizonyítással eldönthessük a rendszeren belül megfogalmazott, tetszőleges matematikai propozíció igazságát vagy hamisságát – akkor volna általános, algoritmikus módszerünk az ilyen propozíciók igazságának eldöntésére. Miért? Mert ha az előbb vázolt eljárással egy bizonyítás utolsó sorában végül is ráakadunk a keresett propozícióra, akkor bebizonyítottuk ezt a propozíciót. Ha, ellenkezőleg, propozíciónk tagadását találjuk meg mint utolsó sort, akkor megcáfoltuk azt. Ha Hilbert rendszere teljes volna, akkor e két lehetőség egyike mindig bekövetkezne (és ha konzisztens, akkor soha nem következnének be egyszerre). Mechanikus eljárásunk így valamelyik lépésben mindig megszakadna, és univerzális algoritmusunk volna a rendszer minden propozíciója igazságának vagy az ellenkezőjének meghatározására. Ez ellentmondana Turing eredményének, hogy matematikai propozíciók eldöntésére nincs általános algoritmus, amint azt a 2. fejezetben bemutattuk. Következésképpen bebizonyítottuk Gödel tételét, hogy semmilyen, Hilbert által áhított rendszer nem lehet teljes a megtárgyalt értelemben.
El tudjuk-e érni, hogy a Turing-gépek minden szükséges művelete végrehajtható legyen csak aritmetikát használva? Másképpen megfogalmazva: ki lehet-e fejezni a természetes számok minden kiszámítható függvényét (azaz rekurzív vagy algoritmikus függvényeket – a Turing-gép munkájának eredményeit) a közönséges aritmetikával? Majdnem igaz, hogy igen, de nem egészen. Egy extra műveletet hozzá kell csatolnunk az aritmetika és logika megszokott szabályaihoz (amelyek között a ∃ és ∀ már ott van). Ez a művelet egyszerűen kiválasztja
„az x legkisebb természetes számot, amelyre K(x) igaz”, ahol K( ) tetszőlegesen adott, aritmetikailag kiszámítható propozíciós függvény – amelyre feltételeztük, hogy van ilyen szám, azaz hogy ∃ x[K(x)] igaz. (Ha nem volna, akkor műveletünk „örökké futna”,53 próbálná megtalálni a kívánt, de nem létező x-et.) Mindenesetre az említett bizonyítás Turing eredménye alapján megállapítja, hogy Hilbert programja a matematika egész ágainak egy formális rendszeren belül végzett számításokká való redukálására valóban tarthatatlan. ha adott egy tetszőleges algoritmus, amely eldönti, hogy egy Turing-gép megáll-e vagy sem, akkor tudunk csinálni olyan Turing-gépet, amelyről mi látjuk, hogy nem áll meg, de az algoritmus nem. (Emlékezzünk vissza, ragaszkodtunk ahhoz, hogy az algoritmusnak helyesen kell tájékoztatnia bennünket, amikor egy Turing-gép meg fog állni, bár olykor elmulaszthatja megmondani, hogy a Turing-gép nem fog megállni – mert maga is a végtelenségig fut.) Így ugyanúgy, mint az előbb a Gödel-tételnél, most is van egy propozíciónk, amelyről meglátásunk elárulja, hogy igaz kell legyen (hogy a Turing-gép nem áll meg), de az adott algoritmus nem képes ezt megmondani nekünk.
Így ha Hilbertnek sikerült volna megtalálnia matematikai rendszerét – axiómák és eljárási szabályok egy rendszerét, amely elég erős, hogy formális bizonyítással eldönthessük a rendszeren belül megfogalmazott, tetszőleges matematikai propozíció igazságát vagy hamisságát – akkor volna általános, algoritmikus módszerünk az ilyen propozíciók igazságának eldöntésére. Miért? Mert ha az előbb vázolt eljárással egy bizonyítás utolsó sorában végül is ráakadunk a keresett propozícióra, akkor bebizonyítottuk ezt a propozíciót. Ha, ellenkezőleg, propozíciónk tagadását találjuk meg mint utolsó sort, akkor megcáfoltuk azt. Ha Hilbert rendszere teljes volna, akkor e két lehetőség egyike mindig bekövetkezne (és ha konzisztens, akkor soha nem következnének be egyszerre). Mechanikus eljárásunk így valamelyik lépésben mindig megszakadna, és univerzális algoritmusunk volna a rendszer minden propozíciója igazságának vagy az ellenkezőjének meghatározására. Ez ellentmondana Turing eredményének, hogy matematikai propozíciók eldöntésére nincs általános algoritmus, amint azt a 2. fejezetben bemutattuk. Következésképpen bebizonyítottuk Gödel tételét, hogy semmilyen, Hilbert által áhított rendszer nem lehet teljes a megtárgyalt értelemben.
El tudjuk-e érni, hogy a Turing-gépek minden szükséges művelete végrehajtható legyen csak aritmetikát használva? Másképpen megfogalmazva: ki lehet-e fejezni a természetes számok minden kiszámítható függvényét (azaz rekurzív vagy algoritmikus függvényeket – a Turing-gép munkájának eredményeit) a közönséges aritmetikával? Majdnem igaz, hogy igen, de nem egészen. Egy extra műveletet hozzá kell csatolnunk az aritmetika és logika megszokott szabályaihoz (amelyek között a ∃ és ∀ már ott van). Ez a művelet egyszerűen kiválasztja
Rekurzívan felsorolható halmazok
Turing és Gödel eredményeinek alapvető kellékeit leírhatjuk grafikus módon a halmazelmélet nyelvén. Ezáltal megszabadulhatunk a formális rendszerektől, a különleges szimbólumoktól, a lényeges pontok mégis megérthetőek. Csak a 0, 1, 2, 3, 4, … természetes számok (véges vagy végtelen) halmazait tekintjük, ezek gyűjteményeit fogjuk vizsgálni, mint például {4, 5, 8}, {0, 57, 100003), {6}, {0}, {1, 2, 3, 4, … , 9999}, {1, 2, 3, 4, …}, {0, 2, 4, 6, 8, …}, vagy éppen a teljes = {0, 1, 2, 3, 4, …} halmaz, vagy a = { } üres halmaz. Csak kiszámíthatósági kérdésekkel fogunk foglalkozni, nevezetesen: „A természetes számok mely típusú halmazait lehet és melyeket nem lehet algoritmus segítségével előállítani?” Van-e már most olyan halmaz, amely rekurzívan felsorolható, de nem rekurzív? Tartsunk egy pillanatnyi szünetet, hogy megjegyezzük, mit vonna ez maga után. Mivel az ilyen halmaz elemeit elő lehet állítani algoritmussal, módunkban áll eldönteni, hogy egy gyaníthatóan a halmazhoz tartozó elem – és amely, tételezzük fel egy pillanatra, ténylegesen a halmaz eleme – valóban a halmazban van-e. Mindössze annyit kell tennünk, hogy algoritmusunkat végigfuttatjuk a halmaz elemein, amíg végül megtaláljuk a vizsgálandó elemet. Tegyük fel azonban, hogy gyanúsított elemünk ténylegesen nincs a halmazban. Algoritmusunk ebben az esetben semmi jóval nem kecsegtet, mert fut a végtelenségig, soha nem jut döntésre. Ehhez a kiegészítő halmazt előállító algoritmusra volna szükségünk. Ha az megtalálja gyanúsítottunkat, akkor biztosan tudjuk, hogy az elem nincs a halmazban. Mindkét algoritmussal könnyű dolgunk lenne. Egyszerűen váltogatnánk a két algoritmust, és valamelyik elkapná a gyanúsítottat. Ez a kellemes helyzet azonban csak a rekurzív halmazoknál valósul meg. Halmazunk most a feltevés szerint csupán rekurzívan felsorolható, de nem rekurzív: a kiegészítő halmaz előállítására nem létezik algoritmus! Így az a furcsa helyzet áll elő, hogy egy halmazban lévő elemről algoritmikusan eldönthetjük, hogy az valóban a halmazban van-e, de algoritmussal nem tudjuk biztosan eldönteni e kérdést olyan elemekre, amelyek nincsenek a halmazban! Van-e már most olyan halmaz, amely rekurzívan felsorolható, de nem rekurzív? Tartsunk egy pillanatnyi szünetet, hogy megjegyezzük, mit vonna ez maga után. Mivel az ilyen halmaz elemeit elő lehet állítani algoritmussal, módunkban áll eldönteni, hogy egy gyaníthatóan a halmazhoz tartozó elem – és amely, tételezzük fel egy pillanatra, ténylegesen a halmaz eleme – valóban a halmazban van-e. Mindössze annyit kell tennünk, hogy algoritmusunkat végigfuttatjuk a halmaz elemein, amíg végül megtaláljuk a vizsgálandó elemet. Tegyük fel azonban, hogy gyanúsított elemünk ténylegesen nincs a halmazban. Algoritmusunk ebben az esetben semmi jóval nem kecsegtet, mert fut a végtelenségig, soha nem jut döntésre. Ehhez a kiegészítő halmazt előállító algoritmusra volna szükségünk. Ha az megtalálja gyanúsítottunkat, akkor biztosan tudjuk, hogy az elem nincs a halmazban. Mindkét algoritmussal könnyű dolgunk lenne. Egyszerűen váltogatnánk a két algoritmust, és valamelyik elkapná a gyanúsítottat. Ez a kellemes helyzet azonban csak a rekurzív halmazoknál valósul meg. Halmazunk most a feltevés szerint csupán rekurzívan felsorolható, de nem rekurzív: a kiegészítő halmaz előállítására nem létezik algoritmus! Így az a furcsa helyzet áll elő, hogy egy halmazban lévő elemről algoritmikusan eldönthetjük, hogy az valóban a halmazban van-e, de algoritmussal nem tudjuk biztosan eldönteni e kérdést olyan elemekre, amelyek nincsenek a halmazban! „Tn(n) megáll” alakú hamis propozíciók, mint előbb megjegyeztük, nem állíthatók elő algoritmussal. Ezért a hamis propozíciók összességükben nem állíthatók elő algoritmussal, mert tetszőleges ilyen algoritmus egyebek között felsorolná az összes fenti „Tn(n) megáll” hamis propozíciót. Hasonlóképpen az összes igaz propozíció sem állítható elő algoritmussal (mert egy ilyen algoritmus triviálisan módosítható volna, hogy az összes hamis propozíciót állítsa elő: egyszerűen venni kellene minden előállított propozíció tagadását). Mivel így az igaz propozíciók nem rekurzívan felsorolhatók (és a hamisak sem), ezért lényegesen összetettebb és mélyebb elrendezést képeznek, mint a rendszeren belül bizonyítható propozíciók. Ez megint Gödel tételének egy megvilágítása: a matematikai igazság fogalma formális bizonyítással csak részben hozzáférhető.
A 4.1. ábrán egy rekurzív halmazt próbáltam vázlatosan ábrázolni mint egy szép egyszerű határvonalakkal rendelkező tartományt; elképzelhetjük, hogy közvetlenül meg lehet mondani, egy adott pont a halmazhoz tartozik-e vagy sem. A képen minden pont egy természetes számot ábrázol. A kiegészítő halmazt szintén egyszerűnek látszó tartomány ábrázolja. A 4.2. ábrán egy rekurzívan felsorolható, de nem rekurzív halmazt próbáltam ábrázolni, mint egy bonyolult határvonalú halmazt. A határ egyik oldalán lévő halmaz – a rekurzívan felsorolható oldal – az elképzelés szerint egyszerűbbnek látszik, mint a másik halmaz. Az ábrák nagyon vázlatosak, és semmilyen értelemben nem szántam „geometriailag pontosnak” azokat. Így nincs jelentősége annak sem, hogy e képeket sima kétdimenziós síkon ábrázoltam! A 4.3. ábrán azt mutattam be vázlatosan, hogyan fekszenek a P, T és A tartományok az halmazon belül.
Rekurzív-e a Mandelbrot-halmaz?
A nem rekurzív halmazoknak meg kell legyen az a tulajdonságuk, hogy nagyon lényeges módon bonyolultak. Bonyolultságuknak bizonyos értelemben le kell győznie minden rendszerezési kísérletet, különben maga a rendszerezés vezetne megfelelő algoritmikus eljáráshoz. Nem rekurzív halmaznál nincs általános algoritmikus út annak eldöntésére, hogy egy elem (vagy „pont”) a halmazhoz tartozik-e vagy sem. A 3. fejezet elején láttunk egy rendkívül bonyolultan kinéző halmazt, a Mandelbrot-halmazt. Bár a meghatározását adó szabályok meglepően egyszerűek, maga a halmaz nagyon bonyolult szerkezetek végtelen változatosságát mutatja. Lehet, hogy a nem rekurzív halmazok egyike mutatkozott meg halandó szemeink előtt? Ám az Olvasónak hamar eszébe jut majd, hogy a bonyolultságnak ezt a mintapéldányát a modern nagy sebességű elektronikus számítógépek technológiájának varázslata idézte fel szemünk számára láthatóan. Nem az algoritmikus működés megtestesülései-e az elektronikus számítógépek? Valóban, ez biztosan igaz, de nem szabad elfelejtenünk, milyen módon hozza létre a számítógép ezeket a képeket. A számítógép úgy ellenőrzi, hogy az Argand-sík egy pontja – egy c komplex szám – a (feketére színezett) Mandelbrot-halmazhoz vagy a (fehéren hagyott) kiegészítő halmazhoz tartozik-e, hogy elindul a 0-tó1, majd z = 0-ra alkalmazza a z → z2 + c leképezést, így kapja c-t, akkor z = c-re alkalmazva c2 + c-t, majd z = c2 + c-re alkalmazva c4 + 2c3 + c2 + c-t és így tovább. Ha ez a 0, c, c2 + c, c4 + 2c3 + c2+ c, … sorozat korlátos marad, akkor a c-t ábrázoló pontot feketére színezzük, egyébként fehér marad. Hogyan mondja meg a gép, hogy az ilyen sorozat korlátos marad-e vagy sem? Elvileg ismernie kell a sorozat végtelen számú tagját! Ez nem kiszámítható dolog. Szerencsére vannak módok arra, hogy a sorozatnak csak véges tagját ismerve megmondjuk, ha a sorozat nem-korlátossá válik. (Ha eléri az origó középpontú, 1 + sugarú kört, akkor biztos, hogy nem korlátos.)Így bizonyos értelemben a Mandelbrot-halmaz kiegészítője (azaz a fehér tartomány) rekurzívan felsorolható. Ha a c komplex szám a fehér tartományban van, akkor ennek a ténynek kiderítésére van algoritmus. Mi a helyzet magával a Mandelbrot-halmazzal – a fekete tartománnyal? Van-e algoritmus annak biztos megállapítására, hogy egy, a fekete tartományban sejtett pont valóban a fekete tartományban van-e? Erre a kérdésre a válasz jelenleg nem ismert.56 Sok munkatársammal, szakértőkkel konzultáltam, egyikük sem tudott ilyen algoritmusról. Nem találkoztak annak bizonyításával sem, hogy ilyen algoritmus nem létezik. A fekete tartományra, legalábbis úgy látszik, nincs ismert algoritmus. Lehet, hogy a Mandelbrot-halmaz kiegészítő halmaza valóban olyan rekurzívan felsorolható halmaz, amely nem rekurzív!Mielőtt e sejtést tovább nyomoznánk, meg kell beszélnünk bizonyos problémákat, amelyeket eddig elkendőztem. Ezeknek majd jelentőségük lesz későbbi vizsgálatainkban a kiszámíthatóságról a fizikában. Az előzőekben valamennyire pontatlan voltam. A „rekurzívan felsorolható” és „rekurzív” kifejezéseket az Argand-sík pontjainak halmazaira alkalmaztam, azaz komplex számok halmazaira. Ezeket a kifejezéseket szigorúan véve csak a természetes számokra vagy más, megszámlálható halmazokra használhatjuk. A 3. fejezetben láttuk, hogy a valós számok nem megszámlálhatóak, így a komplex számok sem lehetnek azok – mert a valós számok speciális komplex számoknak tekinthetők, nevezetesen olyanoknak, amelyek képzetes része eltűnik. A valóságban pontosan „olyan sok” komplex szám van, mint amennyi valós, nevezetesen „ ”. (A komplex és valós számok között úgy lehet például egy-egy értelmű kapcsolatot létesíteni, hogy vesszük minden komplex szám valós és képzetes részének tizedes kifejtését, és ezekből felváltva véve jegyeket, összefésüljük őket: a 3,6781… + i 512,975… komplex szám például az 50132,6977851… valós számnak felel meg.)E probléma elkerülésének egyik módja az lehetne, ha csak a kiszámítható komplex számokra szorítkoznánk, mert a 3. fejezetben láttuk, hogy a kiszámítható valós számok – és ezért a kiszámítható komplex számok is – valóban megszámlálhatók. Ám van ezzel egy komoly nehézség: nincs általános algoritmus annak eldöntésére, hogy két, megfelelő algoritmusukkal adott, kiszámítható szám egyenlő-e egymással vagy sem! (Különbségüket képezhetjük algoritmikusan, de azt nem tudjuk algoritmikusan eldönteni, hogy e különbség nulla-e vagy sem. Képzeljünk el két algoritmust, amelyek rendre a 0,99999… és 1,00000… jegyeket állítják elő, de soha nem tudhatjuk, hogy a 9-esek vagy a 0-k a végtelenségig folytatódnak-e, azaz a két szám egyenlő, vagy egyszer csak más jegy is megjelenik, és a számok nem egyenlőek.) Így soha nem tudhatjuk, hogy e két szám egyenlő-e. Ennek velejárója, hogy még az olyan egyszerű halmazra, mint az Argand-sík egység-körlemeze (azon pontok halmaza, amelyek távolsága az origótól nem nagyobb egy egységnél, azaz a fekete tartomány a 4.4. ábrán) nem lenne algoritmus annak biztos eldöntésére, hogy egy komplex szám rajta van-e a körlemezen. A probléma nem a tartomány belső pontjainál (nem is a körlemezen kívül lévőknél), hanem pont a körlemez szélén, azaz magán az egységkörön fekvőknél lép fel. Az egységkört a körlemez részének tekintjük. Tegyük fel, hogy van egy algoritmusunk, amely előállítja egy komplex szám valós és képzetes részének jegyeit. Ha gyanítjuk is, hogy e komplex szám ténylegesen az egységkörön fekszik, nem tudunk erről kétséget kizáróan megbizonyosodni. Nincs algoritmus annak eldöntésére, hogy az x2 + y2 kiszámítható szám valóban egyenlő-e 1-gyel vagy sem, lévén ez a feltétele annak, hogy az x + iy kiszámítható komplex szám az egységkörön fekszik-e vagy sem. Világos, hogy nem ez az, amit akarunk. Az egység-körlemeznek bizonyára rekurzívnak kellene számítania! Nincs sok nála egyszerűbb halmaz! A probléma megkerülésének egy módja az volna, hogy a határvonalat figyelmen kívül hagyjuk. A belső vagy a külső rész pontjainál biztosan létezik algoritmus e tény kiderítésére. (Állítsuk elő egyszerűen x2 + y2 jegyeit, egyiket a másik után, és egyszer csak találunk a tizedespont után egy 9-től különböző jegyet a 0,99999…-ben vagy egy 0-tól különböző jegyet az 1,00000…-ban.) Ebben az értelemben az egység-körlemez rekurzív. Matematikailag azonban e nézőpont eléggé veszélyes, mert a bizonyításokban gyakran az a lényeges, mi történik a határokon. Lehet viszont, hogy a fizika számára megfelelő az ilyen szemlélet. Később majd újra meg kell fontolnunk ezt a kérdést.Elfogadhatunk egy másik, rokon nézőpontot, amely egyáltalán nem hivatkozik a kiszámítható komplex számokra. Ahelyett, hogy a kérdéses halmazon belül vagy kívül fekvő komplex számokat próbálnánk felsorolni, olyan algoritmust keresünk, amely adott komplex számra eldönti, hogy a halmazban vagy a halmaz kiegészítőjében fekszik-e. Az „adott” szón azt értem, hogy minden ellenőrzésre kerülő komplex számnál – esetleg valamilyen bűvös úton – megkapjuk a valós és képzetes rész egymás után következő jegyeit, annyit, amennyit csak óhajtunk. Nem követelem meg, hogy e jegyek megismerésére legyen ismert vagy ismeretlen algoritmus. A komplex számok egy halmazát „rekurzívan felsorolhatónak” tekintenénk, ha létezne a következő tulajdonságú algoritmus: amikor csak az elmondott módon megkapná a jegyek ilyen sorozatát, akkor véges számú lépés után akkor és csak akkor mondaná azt, hogy „igen”, ha a komplex szám ténylegesen a halmazban fekszik. Kiderül, hogy ez a nézőpont, akárcsak az előbb javasolt első, „nem vesz tudomást” a határokról. Így ebben az értelemben az egység-körlemez belseje és külseje is rekurzívan felsorolhatónak számítana, míg maga a határvonal nem.Számomra nem egészen világos, hogy e nézőpontok egyike vagy másika az, amire igazán szükségünk van.57 A Mandelbrot-halmazra alkalmazva a „határról nem veszünk tudomást” filozófia sokat elveszthet a halmaz bonyolultságából. E halmaz részben „foltokból” – belső résszel rendelkező tartományokból –, részben „indákból” áll. A legszélsőségesebb bonyodalmak az indáknál látszanak, amelyek a legvadabbul tekereghetnek. Az indák azonban nem fekszenek a halmaz belsejében, így „nem vennénk tudomást róluk”, ha elfogadnánk e két filozófia egyikét. Még így, csak a foltokat tekintve sem világos, hogy a Mandelbrot-halmaz rekurzív-e. A kérdés, úgy látszik, egy a halmazra vonatkozó, nem bizonyított sejtésen nyugszik: olyan-e ez a halmaz, mint amilyet „lokálisan összefüggő”-nek neveznek? Nem szándékozom most magyarázni e kijelentés értelmét vagy fontosságát. Csupán azt kívánom jelezni, hogy ezek nehéz problémák, és a Mandelbrot-halmazzal kapcsolatban olyan kérdéseket vetnek fel, amelyek még megoldatlanok, és amelyek közül egyesek a jelenlegi matematikai kutatások élvonalába tartoznak. Vannak más elfogadható nézőpontok is annak a problémának megkerülésére, hogy a komplex számok nem megszámlálhatóak. Ahelyett, hogy az összes kiszámítható komplex számot tekintenénk, szorítkozhatunk e számok egy megfelelő részhalmazára, amelynek az a tulajdonsága, hogy kiszámítható módon eldönthető, egyenlő-e két eleme vagy sem. Egy egyszerű ilyen részhalmaz a „racionális” komplex számok halmaza, amelyek valós és képzetes része egyaránt racionális. Nem hiszem azonban, hogy sokat mondana a Mandelbrot-halmaz indáiról, lévén e nézőpont nagyon korlátozó. Valamivel kielégítőbb lenne az algebrai számok használata – azoké a komplex számoké, amelyek egész együtthatós algebrai egyenletek megoldásai. Például a 129z7 – 33z5 + 725z4 + 16z3 – 2z – 3 = 0 egyenlet minden megoldása algebrai szám. Az algebrai számok megszámlálhatók és kiszámíthatók, és kiszámítható dolog annak eldöntése, hogy két ilyen szám egyenlő-e. (Kiderül, hogy közülük sok van az egységkörön és a Mandelbrot-halmaz indáin.) A kérdés, ha tetszik, úgy fogalmazható, hogy e számok szerint rekurzív-e a Mandelbrot-halmaz vagy sem.Lehet, hogy az algebrai számok alkalmasak lennének e két most tárgyalt halmaz esetében, de nem oldják meg általánosságban az összes nehézséget. Tekintsük ugyanis az y ≥ ex összefüggéssel meghatározott halmazt (a 4.5. ábra fekete tartományát), ahol x + iy(= z) az Argand-sík pontja. A halmaznak és kiegészítőjének belseje rekurzívan felsorolható bármelyik előbb kifejtett nézőpont szerint, azonban a határ, az y = ex (F. Lindemann 1882-ben bebizonyított nevezetes tétele szerint) csak egyetlen algebrai pontot tartalmaz, nevezetesen a z = i pontot. Ebben az esetben a határ algoritmikus természetének felkutatásában az algebrai számok nem segítenek! Nem lenne nehéz megtalálni a kiszámítható számok egy másik alosztályát, amely kielégítő lenne e speciális esetben, de az emberben megmarad az az erős érzés, hogy a helyes nézőpontot még nem találtuk meg.
Vannak más elfogadható nézőpontok is annak a problémának megkerülésére, hogy a komplex számok nem megszámlálhatóak. Ahelyett, hogy az összes kiszámítható komplex számot tekintenénk, szorítkozhatunk e számok egy megfelelő részhalmazára, amelynek az a tulajdonsága, hogy kiszámítható módon eldönthető, egyenlő-e két eleme vagy sem. Egy egyszerű ilyen részhalmaz a „racionális” komplex számok halmaza, amelyek valós és képzetes része egyaránt racionális. Nem hiszem azonban, hogy sokat mondana a Mandelbrot-halmaz indáiról, lévén e nézőpont nagyon korlátozó. Valamivel kielégítőbb lenne az algebrai számok használata – azoké a komplex számoké, amelyek egész együtthatós algebrai egyenletek megoldásai. Például a 129z7 – 33z5 + 725z4 + 16z3 – 2z – 3 = 0 egyenlet minden megoldása algebrai szám. Az algebrai számok megszámlálhatók és kiszámíthatók, és kiszámítható dolog annak eldöntése, hogy két ilyen szám egyenlő-e. (Kiderül, hogy közülük sok van az egységkörön és a Mandelbrot-halmaz indáin.) A kérdés, ha tetszik, úgy fogalmazható, hogy e számok szerint rekurzív-e a Mandelbrot-halmaz vagy sem.Lehet, hogy az algebrai számok alkalmasak lennének e két most tárgyalt halmaz esetében, de nem oldják meg általánosságban az összes nehézséget. Tekintsük ugyanis az y ≥ ex összefüggéssel meghatározott halmazt (a 4.5. ábra fekete tartományát), ahol x + iy(= z) az Argand-sík pontja. A halmaznak és kiegészítőjének belseje rekurzívan felsorolható bármelyik előbb kifejtett nézőpont szerint, azonban a határ, az y = ex (F. Lindemann 1882-ben bebizonyított nevezetes tétele szerint) csak egyetlen algebrai pontot tartalmaz, nevezetesen a z = i pontot. Ebben az esetben a határ algoritmikus természetének felkutatásában az algebrai számok nem segítenek! Nem lenne nehéz megtalálni a kiszámítható számok egy másik alosztályát, amely kielégítő lenne e speciális esetben, de az emberben megmarad az az erős érzés, hogy a helyes nézőpontot még nem találtuk meg.
 Vannak más elfogadható nézőpontok is annak a problémának megkerülésére, hogy a komplex számok nem megszámlálhatóak. Ahelyett, hogy az összes kiszámítható komplex számot tekintenénk, szorítkozhatunk e számok egy megfelelő részhalmazára, amelynek az a tulajdonsága, hogy kiszámítható módon eldönthető, egyenlő-e két eleme vagy sem. Egy egyszerű ilyen részhalmaz a „racionális” komplex számok halmaza, amelyek valós és képzetes része egyaránt racionális. Nem hiszem azonban, hogy sokat mondana a Mandelbrot-halmaz indáiról, lévén e nézőpont nagyon korlátozó. Valamivel kielégítőbb lenne az algebrai számok használata – azoké a komplex számoké, amelyek egész együtthatós algebrai egyenletek megoldásai. Például a
Vannak más elfogadható nézőpontok is annak a problémának megkerülésére, hogy a komplex számok nem megszámlálhatóak. Ahelyett, hogy az összes kiszámítható komplex számot tekintenénk, szorítkozhatunk e számok egy megfelelő részhalmazára, amelynek az a tulajdonsága, hogy kiszámítható módon eldönthető, egyenlő-e két eleme vagy sem. Egy egyszerű ilyen részhalmaz a „racionális” komplex számok halmaza, amelyek valós és képzetes része egyaránt racionális. Nem hiszem azonban, hogy sokat mondana a Mandelbrot-halmaz indáiról, lévén e nézőpont nagyon korlátozó. Valamivel kielégítőbb lenne az algebrai számok használata – azoké a komplex számoké, amelyek egész együtthatós algebrai egyenletek megoldásai. Például aA nemrekurzív matematika néhány példája
A matematika nagyon sok területén merülnek fel nem rekurzív problémák. Így vizsgálhatjuk az olyan problémák osztályát, amelyekre a válasz vagy „igen”, vagy „nem”, de e két lehetőség közötti választásra nem létezik általános algoritmus. A problémák egyes ilyen osztályai különösen egyszerűnek látszanak. .........a diofantoszi aritmetika, alkotórészeinek elemi természete ellenére, a nemalgoritmikus matematika része!58
Valamivel kevésbé elemi példa a sokaságok topologikus ekvivalenciája. Ezt csak röviden említem, mert elképzelhető, hogy van szerepe a 8. fejezetben vizsgált kérdésekben. Hogy megértsük, mi egy „sokaság”, tekintsünk először egy füzér hurkot, amely egydimenziós sokaság, azután egy zárt felületet, egy kétdimenziós sokaságot. Majd próbáljunk elképzelni egyfajta „felületet”, amelynek három vagy magasabb számú dimenziója lehet. Két sokaság „topologikus ekvivalenciája” azt jelenti, hogy az egyik folytonos módon – vágás vagy ragasztás nélkül – a másikba deformálható. Így egy gömbfelület és egy kocka felszíne topologikusan ekvivalensek, viszont mindkettő topologikusan inekvivalens egy gyűrű vagy egy teáscsésze felületével – az utóbbi kettő egymással topologikusan ekvivalens. Kétdimenziós sokaságoknál van algoritmus annak eldöntésére, hogy közülük kettő topologikusan ekvivalens-e – ez valójában az egyes felületek „fogantyúi” számának megszámlálása. Három dimenzióban a kérdésre válasz az írás időpontjában nem ismeretes, de négy vagy több dimenzióban az ekvivalencia eldöntésére nincs algoritmus. A négydimenziós esetnek feltehetően van jelentősége a fizikában, mert Einstein általános relativitáselmélete szerint a tér és az idő együtt négyes sokaságot képez (lásd 5. fejezet). Geroch és Hartle (1987) azt vetette fel, hogy e nem algoritmikus tulajdonságnak jelentősége lehet a „kvantumgravitációban” (vö. még 8. fejezet). Utolsó nem rekurzív matematikai példaként nézzük az euklideszi sík sokszögekkel való lefedésének kérdését. Adott véges számú különböző alakzat, és azt kérdezzük, le lehet-e fedni kizárólag ezekkel a síkot tökéletesen, rések és átfedések nélkül. Az alakzatok ilyen elrendezését a sík egy parkettázásának nevezik. Jól tudjuk, hogy csak négyzetekkel vagy csak egyenlő oldalú háromszögekkel vagy csak szabályos hatszögekkel (10. fejezet, 10.2. ábra) az ilyen parkettázás lehetséges, de csak szabályos ötszögekkel nem. A sík sokféle más alakzattal parkettázható, mint például a 4.6. ábrákon bemutatott kétféle szabálytalan ötszög bármelyikével. Két alakzattal a parkettázás szebben kidolgozott lehet. A 4.7. ábrán két egyszerű példa látható. Mindezeknek a példáknak megvan az a tulajdonsága, hogy periodikusak; két független irányban pontosan ismétlődnek. Matematikai nyelven azt mondjuk, hogy van egy periódus-paralelogramma – egy paralelogramma, amelyet valahogy megjelölve és a két irányban oldalaival párhuzamosan újra és újra lerakva megkapjuk az adott parkettamintát. Egy példa a 4.8. ábrán látható, a bal oldal periodikus parkettázást mutat egy kürt alakú parkettával, a jobb oldal a kapcsolatot mutatja a periódus-paralelogrammával való periodikus parkettázással.
Talán figyelemre méltó, hogy a matematika egy ilyen nyilvánvalóan „triviális” területe – nevezetesen a sík lefedése egyforma alakzatokkal –, amely majdnem a „gyermekjátékhoz” hasonlít, valójában a nem rekurzív matematika része. E területen sok a nehéz és megoldatlan probléma. Nem tudjuk például azt, van-e egyetlen parkettából álló aperiodikus halmaz.Wang, Berger és Robinson a parkettázási problémában négyszög alapú parkettákat használt. Magam tetszőleges alakú sokszögeket megengedtem; az egyes parketták alakjának kiderítésére szükség volna valamilyen megfelelően kiszámítható módszerre. Egy lehetőség az volna, ha a csúcsokat az Argand-sík pontjaiként adnánk meg, ekkor tökéletesen jól leírhatnánk azokat algebrai számokkal.
Talán figyelemre méltó, hogy a matematika egy ilyen nyilvánvalóan „triviális” területe – nevezetesen a sík lefedése egyforma alakzatokkal –, amely majdnem a „gyermekjátékhoz” hasonlít, valójában a nem rekurzív matematika része. E területen sok a nehéz és megoldatlan probléma. Nem tudjuk például azt, van-e egyetlen parkettából álló aperiodikus halmaz.Wang, Berger és Robinson a parkettázási problémában négyszög alapú parkettákat használt. Magam tetszőleges alakú sokszögeket megengedtem; az egyes parketták alakjának kiderítésére szükség volna valamilyen megfelelően kiszámítható módszerre. Egy lehetőség az volna, ha a csúcsokat az Argand-sík pontjaiként adnánk meg, ekkor tökéletesen jól leírhatnánk azokat algebrai számokkal.
A Mandelbrot-halmaz és a nemrekurzív matematika
Térjünk most vissza a Madelbrot-halmazzal foglalkozó korábbi fejtegetésünkhöz. Az illusztráció kedvéért fel fogom tételezni, hogy valamilyen megfelelő értelemben a halmaz nem rekurzív. Ekkor, mivel kiegészítője rekurzívan felsorolható, ezért a halmaz maga nem lehet olyan. Úgy vélem, hogy a Mandelbrot-halmaz egy pár dologra megtanít bennünket a nem rekurzív halmazok és a nem rekurzív matematika természetét illetően.Térjünk vissza a 3.2. ábrához, amellyel a 3. fejezet elején találkoztunk. Vegyük észre, hogy a halmaz legnagyobb része az a nagy szív alakú tartomány, amelyet a 4.13. ábrán A-val jelöltem. Az alakzat neve kardioid, belsejét úgy lehet matematikailag definiálni, mint az Argand-sík azon c pontjainak halmaza, amelyekre c = z – z2, ahol z olyan komplex szám, amelynek távolsága a kezdőponttól kisebb, mint 1/2. Ez a halmaz a korábban javasolt értelemben biztosan rekurzívan felsorolható: létezik algoritmus, amely a tartomány egy belső pontjára alkalmazva kimutatja, hogy a pont valóban a tartomány belsejében van. A tényleges algoritmus a fenti képletből könnyen megkapható.Tekintsük most a fő kardioidtól közvetlenül balra lévő, korongszerű tartományt (a 4.13. ábrán a B tartományt). Belseje a c = z – 1
pontok halmaza, ahol z távolsága a kezdőponttól kisebb, mint 1/4. E tartomány valóban egy korong belseje – egy egzakt kör belsejében lévő pontok halmaza. Ez a fenti értelemben ismét rekurzívan felsorolható. Mi a helyzet a kardioid többi „szemölcsével”? Nézzük meg közülük a két legnagyobbat. Ezek azok a nagyjából kör alakú foltok, amelyek a 3.2. ábrán közelítőleg a kardioid tetején és alján helyezkednek el, és amelyeket a 4.13. ábrán C1-gyel és C2-vel jelöltem. Ezek pontjai a c3 + 2c2 + (1 – z)c + (1 – z)2 = 0 egyenlettel adhatók meg, ahol z most a kezdőponttól 1/8-nál kisebb távolságra lévő pontokon fut végig. Valójában az egyenlet nem csak ezt a két foltot adja meg, hanem a 3.2. ábrán balra látható „bébi”-kardioidszerű alakzatot is – a 3.1. ábra fő tartományát – amelyet a 4.13. ábrán C3-mal jelöltem. E tartományok (együtt vagy külön-külön) újra rekurzívan felsorolható halmazokat képeznek (a korábban javasolt értelemben) egyszerűen azért, mert a fenti képlet létezik.
Korábbi sugalmazásom ellenére, mely szerint a Mandelbrot-halmaz esetleg nem rekurzív, a legnagyobb területeket már tisztába tudtuk tenni teljesen ........a legáltalánosabb problémákat, amelyekbe sokszor beleütközünk, gyakran tudjuk egyszerű algoritmikus eljárásokkal kezelni – amelyek esetleg már évszázadok óta ismertek. Egyesek azonban kiszöknek a hálóból, és kezelésükhöz kifinomultabb eljárásokra van szükség. Az ilyenek természetesen különösen felkeltik a matematikusok érdeklődését, és még hatékonyabb módszerek kidolgozására ösztönzik őket. Ehhez pedig mélyebb és mélyebb bepillantásokra van szükség a matematika e részének természetébe. Talán így értjük meg a fizikai világot is
Bonyolultságelmélet
Az algoritmusok természetéről, létezéséről és korlátairól most és az előző fejezetekben kifejtett érveim nagyon sok tekintetben „elvi” jellegűek voltak. Egyáltalán nem vizsgáltam annak kérdését, hogy a felmerülő algoritmusoknak várhatóan lesz-e gyakorlati értékük. Még azoknál a problémáknál is, amelyeknél világos, hogy léteznek algoritmusok, és az is, hogy hogyan kell ezeket felépíteni, sok ötletességre és kemény munkára lehet szükség, hogy használhatóvá tegyék ezeket az algoritmusokat. Érdekesebbek azok a problémák, amelyeknél polinomiális idő alatt le lehet írni a választ, sőt még ellenőrizni is lehet helyességét. A problémák (algoritmikusan megoldható részének) fontos osztályát jellemzi ez a tulajdonság. Ezeket NP problémáknak (osztályoknak) nevezik. Pontosabban szólva, ha egy NP-ben lévő problémaosztály egy problémájának van megoldása, akkor az algoritmus megadja ezt a megoldást, és polinomiális idő alatt ellenőrizhető kell legyen, hogy a javasolt megoldás valóban megoldás. Azokban az esetekben, amikor a problémának nincs megoldása, az algoritmus ezt megmondja, de ellenőrizni nem kell – polinomiális időben vagy máshogy –, hogy valóban nincs megoldás.64NP problémák sok összefüggésben felbukkannak mind magán a matematikán belül, mind a gyakorlati világban. Mondok egy egyszerű matematikai példát: azt a problémát, hogyan találjunk egy gráfban olyat, amit „Hamilton-kör”-nek neveznek (meglehetősen ijesztő név egy rendkívül egyszerű dologra). „Gráfon” pontok vagy „csúcsok” véges együttesét értjük, amelyben bizonyos számú pár össze van kötve vonalakkal – ezek a gráf „élei”. (Most nem érdekelnek a geometriai vagy a „távolság”-tulajdonságok, csak az, melyik csúcs melyik csúccsal van összekötve. Így nem számít, hogy a csúcsok egy síkban vannak-e – feltéve, hogy nem törődünk az élek kereszteződéseivel – vagy háromdimenziós térben.) A Hamilton-kör egy zárt út (vagy hurok), amely csak a gráf éleiből áll, és minden csúcson pontosan egyszer megy keresztül. A 4.14. ábrán példaként egy gráf látható, benne egy Hamilton-körrel. A Hamilton-kör probléma annak eldöntése, hogy tetszőlegesen adott gráfban létezik-e Hamilton-kör vagy sem, és amikor létezik, akkor egy ilyen explicit megadása.E probléma valójában nemcsak NP, hanem ún. NP-teljes. Ez azt jelenti, hogy tetszőleges más NP probléma átalakítható ebbe polinomiális idő alatt – így ha valaki elegendően okos lenne, és találna egy algoritmust, amely polinomiális idő alatt megoldja a Hamilton-kör problémát, azaz megmutatná, hogy a probléma valóban P-ben van, akkor ebből következne, hogy minden NP probléma P-ben van! Ebből nagyon fontos dolgok következnének. Egy P-ben lévő problémát általánosan „kezelhetőnek” (azaz „elfogadható idő alatt megoldhatónak”) tekintenek, gyors modern számítógépen, ésszerűen nagy n mellett, míg egy NP-ben lévőt, amely nincs P-ben, „kezelhetetlennek” (azaz bár elvileg megoldhatónak, „gyakorlatilag megoldhatatlannak”) ésszerűen nagy n mellett – függetlenül a számítógépek műveleti sebességében bekövetkezhető, bármilyen jellegű növekedéstől. (Az az idő, amennyit egy nem P-ben lévő NP probléma megoldása ténylegesen igénybe venne, nagy n-re gyorsan felülmúlná a világegyetem életkorát, ami gyakorlati problémánál nem sok reménnyel kecsegtet!) Bármilyen okos algoritmus, amely polinomiális idő alatt megoldja a Hamilton-kör problémát, átalakítható volna olyan algoritmusba, amely polinomiális idő alatt megold tetszőleges más NP problémát!Egy másik, NP-teljes probléma65 „az utazó kereskedő problémája”, amely meglehetősen hasonlít a Hamilton-kör problémához, csak ebben az élekhez számok vannak rendelve, és azt a Hamilton-kört keresi, amelyre a számok összege (a kereskedő által beutazott „távolság”) minimális. Az utazó kereskedő problémájának polinomiális idő alatti megoldása ismét minden más NP probléma polinomiális idő alatti megoldásához vezetne. (Ha ilyen megoldást találnának, az címoldalra kerülő újsághír lenne! Ott vannak ugyanis a titkos kódrendszerek, amelyeket az elmúlt néhány év során vezettek be, és amelyek a nagy egész számok szorzattá bontásának problémájára támaszkodnak, lévén ez egy másik NP probléma. Ha ez megoldható volna polinomiális idő alatt, akkor az ilyen kódokat a nagy teljesítményű, modern számítógépek valószínűleg könnyen megfejtenék, de ha nem, akkor a kódok biztonságban vannak. (Lásd Gardner 1989.)A szakértők között általános az a vélemény, hogy tetszőleges Turing-gépszerű eszközzel lehetetlen polinomiális idő alatt megoldani egy NP-teljes problémát, és következésképp P és NP nem azonos. Nagyon valószínű, hogy e sejtés igaz, de még senkinek sem sikerült bebizonyítania. Ez marad a bonyolultságelmélet legfontosabb megoldatlan problémája.
Bonyolultság és kiszámíthatóság a fizikai dolgokban
A bonyolultságelmélet fontos a könyvünkben található fejtegetések szempontjából, mert egy másik kérdést kínál, valamennyire eltérőt attól, hogy a dolgok algoritmikusak-e vagy sem: nevezetesen azt, hogy vajon azok a dolgok, amelyekről tudjuk, hogy algoritmikusak, hasznos módon algoritmikusak-e. A későbbi fejezetekben kevesebbet kell majd foglalkoznom a bonyolultságelmélet kérdéseivel, többet a kiszámíthatósággal. Hajlok ugyanis azt hinni (bár kétségtelen, hogy teljesen megalapozatlanul), hogy eltérően a kiszámíthatóság alapvető kérdésétől, a bonyolultságelmélet nem játszik központi szerepet a szellemi jelenségekben. Mi több, úgy érzem, hogy az algoritmusok gyakorlatiasságának kérdéseit a bonyolultságelmélet mai állásában alig érinti.Persze tévedhetek is a bonyolultság szerepének megítélésében. Amint azt később majd kifejtem (9. fejezet), a bonyolultságelmélet a valódi fizikai objektumokra jelentősen eltérő lehet attól, amit éppen most tárgyaltunk. Hogy e lehetséges különbség láthatóvá váljék, ahhoz ki kellene használni a kvantummechanikának – az atomok és molekulák viselkedése és sok más, esetleg sokkal nagyobb skálán is fontos jelenség e titokzatos, mégis hatékony és pontos elméletének – mágikus tulajdonságait. Ezzel az elmélettel a 6. fejezetben fogunk megismerkedni. A David Deutsch (1985) által felvetett legújabb elképzelések szerint elvileg lehetséges „kvantumszámítógépet” készíteni, amely polinomiális idő alatt megoldhat nem P-ben lévő problémákat. Jelenleg egyáltalán nem világos, hogyan kell olyan valódi fizikai eszközt készíteni, amely (megbízhatóan) úgy viselkedik, mint egy kvantumszámítógép – és ráadásul az eddig számításba vett problémaosztály határozottan mesterséges –, ám az elméleti lehetőség, hogy egy kvantumfizikai eszköz képes lehet tökéletesíteni egy Turing-gépet, úgy látszik, az asztalunkon van.Lehetséges-e, hogy az emberi agy, amelyet e tárgyalásban „fizikai eszköznek” tekintek, noha meghökkentően finom tervezésűnek és bonyolultnak tartom, kihasználja a kvantumelmélet varázslatait? Értjük-e a módját, hogyan lehet a kvantumos jelenségeket előnyösen felhasználni problémák megoldásában vagy ítéletek kialakításában? Elképzelhető-e, hogy még a mai kvantumelméletnél is „mélyebbre” kell mennünk, hogy e lehetséges előnyöket kiaknázzuk? Reális-e az a lehetőség, hogy valóságos fizikai eszközök tökéletesíthetik a Turing-gépek bonyolultságelméletét? És mit mond a kiszámíthatóság elmélete ezekre az eszközökre?
Ez a fenti bekezdés az ahonnan még sokkal érdekesebbé vált számomra az utazás.
Lehetséges-e, hogy az emberi agy, amelyet e tárgyalásban „fizikai eszköznek” tekintek, noha meghökkentően finom tervezésűnek és bonyolultnak tartom, kihasználja a kvantumelmélet varázslatait?
-kérdi Penrose.
Hogy e kérdésekkel foglalkozhassunk, el kell hagynunk a tiszta matematikát, és a következő fejezetekben azt kell megvizsgálnunk, hogyan viselkedik a fizika világ!
és azt igéri átvisz egy másik világba, a nem elvontba...
A bonyolultságelmélet fontos a könyvünkben található fejtegetések szempontjából, mert egy másik kérdést kínál, valamennyire eltérőt attól, hogy a dolgok algoritmikusak-e vagy sem: nevezetesen azt, hogy vajon azok a dolgok, amelyekről tudjuk, hogy algoritmikusak, hasznos módon algoritmikusak-e. A későbbi fejezetekben kevesebbet kell majd foglalkoznom a bonyolultságelmélet kérdéseivel, többet a kiszámíthatósággal. Hajlok ugyanis azt hinni (bár kétségtelen, hogy teljesen megalapozatlanul), hogy eltérően a kiszámíthatóság alapvető kérdésétől, a bonyolultságelmélet nem játszik központi szerepet a szellemi jelenségekben. Mi több, úgy érzem, hogy az algoritmusok gyakorlatiasságának kérdéseit a bonyolultságelmélet mai állásában alig érinti.Persze tévedhetek is a bonyolultság szerepének megítélésében. Amint azt később majd kifejtem (9. fejezet), a bonyolultságelmélet a valódi fizikai objektumokra jelentősen eltérő lehet attól, amit éppen most tárgyaltunk. Hogy e lehetséges különbség láthatóvá váljék, ahhoz ki kellene használni a kvantummechanikának – az atomok és molekulák viselkedése és sok más, esetleg sokkal nagyobb skálán is fontos jelenség e titokzatos, mégis hatékony és pontos elméletének – mágikus tulajdonságait. Ezzel az elmélettel a 6. fejezetben fogunk megismerkedni. A David Deutsch (1985) által felvetett legújabb elképzelések szerint elvileg lehetséges „kvantumszámítógépet” készíteni, amely polinomiális idő alatt megoldhat nem P-ben lévő problémákat. Jelenleg egyáltalán nem világos, hogyan kell olyan valódi fizikai eszközt készíteni, amely (megbízhatóan) úgy viselkedik, mint egy kvantumszámítógép – és ráadásul az eddig számításba vett problémaosztály határozottan mesterséges –, ám az elméleti lehetőség, hogy egy kvantumfizikai eszköz képes lehet tökéletesíteni egy Turing-gépet, úgy látszik, az asztalunkon van.Lehetséges-e, hogy az emberi agy, amelyet e tárgyalásban „fizikai eszköznek” tekintek, noha meghökkentően finom tervezésűnek és bonyolultnak tartom, kihasználja a kvantumelmélet varázslatait? Értjük-e a módját, hogyan lehet a kvantumos jelenségeket előnyösen felhasználni problémák megoldásában vagy ítéletek kialakításában? Elképzelhető-e, hogy még a mai kvantumelméletnél is „mélyebbre” kell mennünk, hogy e lehetséges előnyöket kiaknázzuk? Reális-e az a lehetőség, hogy valóságos fizikai eszközök tökéletesíthetik a Turing-gépek bonyolultságelméletét? És mit mond a kiszámíthatóság elmélete ezekre az eszközökre?
Ez a fenti bekezdés az ahonnan még sokkal érdekesebbé vált számomra az utazás.
Lehetséges-e, hogy az emberi agy, amelyet e tárgyalásban „fizikai eszköznek” tekintek, noha meghökkentően finom tervezésűnek és bonyolultnak tartom, kihasználja a kvantumelmélet varázslatait?
-kérdi Penrose.
Hogy e kérdésekkel foglalkozhassunk, el kell hagynunk a tiszta matematikát, és a következő fejezetekben azt kell megvizsgálnunk, hogyan viselkedik a fizika világ!
és azt igéri átvisz egy másik világba, a nem elvontba...
5. A klasszikus világ
A fizikai elmélet helyzete
Mit kell tudnunk a Természet működéséről, hogy megállapíthassuk, hogyan lehet része a tudatosság? Számít-e igazán, milyen törvények kormányozzák a testeket és agyakat összetevő elemeket? Ha tudatos érzékelésünk csupán algoritmusok lejátszása, ahogy azt sok MI-párti elhitetné velünk, akkor nincs komoly jelentősége annak, hogy ténylegesen mik is ezek a törvények. Minden eszköz, amely képes végrehajtani egy algoritmust, éppen olyan jó volna, mint bármelyik másik. Másrészt tudatosságérzésünk esetleg több, mint a puszta algoritmusok összessége. Talán valóban fontosak felépítésünk részletei, mint ahogy fontosak azok a pontos fizikai törvények, amelyek az anyagot kormányozzák, amelyből vagyunk. Talán meg kell értenünk, mi az a mély minőség, amely az anyag igazi természete mögött rejtőzik, és meghatározza a módot, amely szerint minden anyagnak viselkednie kell. A fizika még nincs ezen a ponton. Még sok a megfejtésre váró titok, még sok mély meglátásra van szükség. A legtöbb fizikus és fiziológus mégis úgy ítélné meg a helyzetet, hogy már eleget tudunk azokról a fizikai törvényekről, amelyek lényegesek az olyan normál méretű objektumok működésében, mint az emberi agy. Noha kétségtelen, hogy az agy mint fizikai rendszer kivételesen bonyolult, és részletes szerkezetéről, lényegi működéséről még rengeteget nem tudunk, mégis kevesen állítanák, hogy a viselkedése alapját képező fizikai elvekről bármi lényegeset ne értenénk.Később majd megemlítek egy, a szokásostól eltérő esetet annak bizonyítására, hogy ellenkezőleg, még nem értjük elég jól a fizikát ahhoz, hogy segítségével agyunk működését, akár csak elvileg is, megfelelően leírhassuk. Ehhez szükség lesz arra, hogy először némi áttekintést adjak a fizika jelenlegi állásáról. E fejezet azzal foglalkozik, amit „klasszikus fizikának” hívnak, amely magában foglalja mind Newton mechanikáját, mind Einstein relativitáselméletét. A „klasszikus” szó itt lényegében azokat az elméleteket jelenti, amelyek a kvantumelmélet megjelenése előtt uralkodtak. Utóbbi nagyjából 1925-re tehető (olyan fizikusok ihletett munkáin keresztül, mint Planck, Einstein, Bohr, Heisenberg, Schrödinger, de Broglie, Born, Jordan, Pauli és Dirac). A kvantumelmélet a határozatlanság, indeterminizmus és titokzatosság elmélete, a molekulák, atomok és szubatomi részecskék viselkedését írja le. A klasszikus elmélet viszont determinisztikus, benne a múlt mindig meghatározza a jövőt. A klasszikus fizikában még így is sok a titokzatos dolog, annak ellenére, hogy a századok során összegyűjtött tudás egészen fantasztikusan pontos képhez juttatott bennünket. Meg kell majd vizsgálnunk a kvantumelméletet is (6. fejezet), mert ellentétben azzal, ami a fiziológusok körében a többségi nézetnek látszik, úgy hiszem, hogy a kvantumos jelenségek valószínűleg fontosak az agy működésében – de ez a következő fejezetek tárgya lesz.Drámainak mondható, amit a tudomány napjainkig elért. Csak körül kell néznünk, hogy tanúsítsuk, milyen rendkívüli erőhöz jutottunk a Természet megértése által. A modern világ technológiája jelentős mértékben az empirikus tapasztalatok nagy gazdagságából származik. Ám a fizikai elmélet az, ami meghatározó módon technológiánk alapjául szolgál, és a fizikai elmélet az, ami most bennünket érdekel. A rendelkezésünkre álló elméletek pontossága igen figyelemreméltó. Ám nem csupán pontosságuk az erősségük, hanem az a körülmény is, hogy pontos és részletes matematikával rendkívül jól kezelhetőnek és ellenőrizhetőnek bizonyultak. Ezek együttesen nyújtanak számunkra egy valóban meggyőző erejű tudományt.E fizikai elmélet jó része nem különösebben új. Ha egy esemény kiemelhető az összes többi elé, akkor az Isaac Newton Principiájának 1687-es megjelentetése. Ez a nagy jelentőségű mű megmutatta, hogyan lehet néhány alapvető fizikai elv alapján megérteni és gyakran meglepő pontossággal megjósolni a fizikai objektumok viselkedésének nagy részét. (A Principia figyelemre méltó fejlődést hozott a matematikai technikában is, bár több gyakorlati módszert később dolgoztak ki Euler és mások.) Newton munkája, amint ő készségesen elismerte, sokban támaszkodott a korábbi gondolkodók eredményeire, akik közül kimagaslik Galileo Galilei, René Descartes és Johannes Kepler. Fontos, alapvető fogalmak még régebbi gondolkodóktól származtak, ilyenek például Platón, Eudoxosz, Eukleidész, Arkhimédész és Appolóniosz geometriai elképzelései. Később majd többet kell ezekről mondanom.Az eltérések Newton dinamikájának alapsémájától később jelentek meg, először James Clerk Maxwellnek a tizenkilencedik század közepén kidolgozott elektromágneses elmélete. Ez nemcsak az elektromos és mágneses mezők klasszikus viselkedésével foglalkozott, hanem a fényével is!66 A fejezet későbbi részében erre a nevezetes elméletre fordítjuk figyelmünket. Maxwell elmélete igen fontos a mai technológia szempontjából, és az is kétségtelen, hogy az elektromágneses jelenségek hozzátartoznak agyunk működéséhez. Kevésbé világos azonban az, hogy lehet-e valami jelentősége gondolkodási folyamatunkban a két nagy relativitáselméletnek, amelyek Albert Einstein nevéhez fűződnek. A speciális relativitáselmélet a Maxwell-egyenletek vizsgálatából fejlődött ki, Henri Poincaré, Hendrick Antoon Lorentz és Einstein alkották meg (később Hermann Minkowski adott elegáns geometriai leírást) abból a célból, hogy megmagyarázzák a testek rejtélyes viselkedését, amikor azok a fénysebességhez közeli sebességgel mozognak. Einstein híres egyenlete, az „E = mc2”, része az elméletnek. Azonban az elmélet hatása a technológiára mindeddig nagyon csekélynek bizonyult (kivéve, amikor a magfizikába szólt bele), és jelentősége agyunk működésében a legjobb esetben is csak periferiálisnak látszik. A speciális relativitáselmélet viszont mond valami mélyet a fizikai valóságról az idő természetével kapcsolatban. A következő fejezetekben látni fogjuk, hogy ez bizonyos rejtett problémákhoz vezet a kvantumelméletben, aminek jelentősége lehet azzal kapcsolatban, ahogy az „idő múlását” érzékeljük. Továbbmenve, először meg kell értenünk a speciális elméletet, csak utána tudjuk megfelelően értékelni Einstein általános relativitáselméletét – azt az elméletet, amely görbült téridő segítségével írja le a gravitációt. Ennek az elméletnek a technológiára eddig majdnem semmi hatása nem volt,67 és szélsőségesen különösnek látszana bármi jelentőséget tulajdonítani neki agyunk működésében! De érdekes módon éppen az általános relativitáselméletnek lesz a legnagyobb a jelentősége későbbi megfontolásainkban, kivált a 7. és 8. fejezetben, ahol térben és időben a legnagyobb távolságokig kell majd elmennünk, hogy megragadjunk valamit a változásokból, amelyekre szerintem szükség van ahhoz, hogy a kvantumelméletről megfelelően koherens képünk alakuljon ki – de erről többet majd később!Ezek a klasszikus fizika nagy területei. Mi a helyzet a kvantumfizikával? Ellentétben a relativitáselmélettel, a kvantumelmélet igazán jelentős hatást kezd kifejteni a technológiára. Ez részben azoknak a felismeréseknek a következménye, amelyeket a kvantumelmélet nyújtott bizonyos technológiailag fontos területeken, mint a kémia és a fémkohászat. Egyesek már azt mondják, hogy ezek a területek tulajdonképpen beolvadtak a fizikába, annak a sok új felismerésnek következtében, amelyeket a kvantumelmélet adott nekünk. Vannak ráadásul egészen új jelenségek, amelyekkel szintén a kvantumelmélet ajándékozott meg, a legismertebb ezek között, azt hiszem, a lézer. Nem lehetséges-e, hogy a kvantumelmélet egyes lényeges pontjai döntő szerepet játszanak abban a fizikában is, amely gondolati folyamataink alapjait képezi?Mi a helyzet a legújabb fizikai felismerésekkel? Egyes olvasók már találkozhattak az olyan izgalmasan kifejezett elképzelésekkel, mint a „kvarkok”, a „GUT” (Grand Unified Theories = nagy egyesített elméletek), az „inflatorikus világegyetem” (lásd a 153. jegyzetet), a „szuperszimmetria”, a „(szuper)húr-elmélet” stb. Hogy néznek ki ezek az új elméletek összehasonlítva azokkal, amelyekre éppen az előbb utaltam? Kell-e tudnunk ezekről is? Azt hiszem, a dolgokat a megfelelő megvilágításba helyezendő, fel kell állítanom az alapvető fizikai elméletek három széles osztályát. Ezekre a következő címkéket akasztom: - SZUPER,
- HASZNOS,
- KÍSÉRLETI.
A SZUPER kategóriába kell tartozzék mindaz, amiről az előző bekezdésekben szó volt. A SZUPER minősítéshez nem tartom fontosnak, hogy az elmélet ellenpélda nélkül alkalmazható legyen a világ jelenségeire, de megkövetelem, hogy olyan tartományban és olyan pontossággal legyen alkalmazható, amely valamilyen értelemben rendkívüli. Ahhoz képest, hogy milyen feltételekhez kötöm a SZUPER minősítést, igazán figyelemre méltó, hogy ebben az osztályban van egyáltalán elmélet! Nincs tudomásom semmilyen más tudomány semmilyen más alapelméletéről, amely jogosan bekerülhetne ebbe az osztályba. Talán a természetes kiválasztódás Darwin és Wallace által javasolt elmélete áll hozzá a legközelebb, de azért még eléggé távol.A SZUPER elméletek legrégebbije az euklideszi geometria, amelyről valamennyit tanultunk az iskolában. A régiek egyáltalán nem tekinthették fizikai elméletnek, pedig valójában az: nagyszerű és nagyon pontos elmélete a fizikai térnek – és a merev testek geometriájának. Miért tekintem inkább fizikai elméletnek, mintsem a matematika egyik ágának? Ironikusan mondhatnánk: amiért e nézetet valljuk, annak egyik legtisztább oka az, hogy ma már tudjuk, az euklideszi geometria mint az életterünkként szolgáló fizikai tér leírása nem teljesen pontos! Einstein általános relativitáselmélete azt mondja nekünk, hogy a tér(idő) gravitációs mező jelenléte esetén „görbült” (azaz nem teljesen euklideszi). Ám ez a tény nem változtatja meg az euklideszi geometria SZUPER jellegét. Méteres tartományban az euklideszi simaságtól való eltérés igazán parányi, a geometria euklideszi módon való kezelésének hibája kisebb, mint egy hidrogénatom átmérője!Jogosan mondhatjuk, hogy a statika elmélete (amely a nyugalomban lévő testekkel foglalkozik), ahogy Arkhimédész, Papposz és Stevin szép tudománnyá fejlesztették, szintén SZUPER-nek minősíthető. Ez az elmélet mára beolvadt a newtoni mechanikába. A dinamikának (a mozgó testek tudományának) a Galilei által 1600 körül bevezetett és Newton által pompás, átfogó elméletté fejlesztett, mély ideái kétségtelenül a SZUPER osztályba kell kerüljenek. A bolygók és holdak mozgására alkalmazva az elmélet megfigyelt pontossága tüneményes – jobb, mint egy a tízmillióhoz. Ugyanaz a newtoni rendszer hasonló pontossággal alkalmazható itt a Földön – és kint a csillagok és galaxisok között. Maxwell elmélete hasonlóképpen rendkívül nagy tartományban érvényes pontosan, az atomok és szubatomi részecskék piciny skálájától kifelé a galaxisok néhány milliószor milliószor milliószor milliószor milliószor milliószor nagyobb skálájáig! (A tartomány kisméretű végén a Maxwell-egyenleteket a kvantummechanika szabályaival kell megfelelően kombinálni.) Ez is bizonnyal kiérdemli a SZUPER minősítést.Einstein speciális relativitáselmélete (melynek előzményei már Poincarénál is fellelhetők, és amit Minkowski elegánsan újrafogalmazott) csodálatosan pontos leírását adja azoknak a jelenségeknek, amelyekben a tárgyak sebessége megközelítheti a fénysebességet – ahol Newton leírása végül botladozni kezd. Einstein legcsodálatosabb és legeredetibb általános relativitáselmélete általánosítja Newton dinamikai (gravitáció-) elméletét, és örökölve annak a bolygók és holdak mozgásának leírásában mutatott minden pontosságát, még meg is javítja azt. Ráadásul megmagyaráz egy sor részletes megfigyelést, amelyek a régi newtoni rendszerrel nem egyeztethetők össze. Ezek egyike (a „kettős pulzár”) azt mutatja, hogy Einstein elméletének pontossága nagyjából 1 a 1014-hez. Mindkét relativitáselméletet – a második magába olvasztja az elsőt – a SZUPER osztályba kell sorolnunk (matematikai eleganciájukért majdnem annyira, mint pontosságukért).A kvantummechanika különösképpen szép és forradalmi elméletével magyarázott jelenségek tartománya, és a pontosság, ahogy a kísérletekkel megegyezik, világosan mondja nekünk, hogy a kvantumelméletet is biztosan SZUPER-nak kell minősítenünk. Az elméletnek ellentmondó megfigyelést nem ismerünk – erejét elsősorban mégsem ez adja, hanem az a számos, mindeddig megmagyarázhatatlan jelenség, amelyet az elmélet most megmagyaráz. A kémia törvényei, az atomok stabilitása, a színképvonalak élessége (vö. 6. fejezet) és megfigyelt, nagyon különös szerkezetük, a szupravezetés (nulla elektromos ellenállás) furcsa jelensége és a lézerek viselkedése csak néhány ezek közül.A SZUPER osztályba kerüléshez magas követelményeket állítok, de ez az, amihez a fizikában hozzászoktunk. Mi a helyzet az újabb elméletekkel? Véleményem szerint csak egy olyan van, amely SZUPER-nek minősíthető, és ez nem is nagyon új: a kvantumelektrodinamika (vagy QED) nevet viselő elmélet, amelyet Jordan, Heisenberg és Pauli munkássága alapozott meg, Dirac fogalmazott meg 1926 és 1934 között, és Bethe, Feynman, Schwinger és Tomonaga tett működőképessé 1947 – 48-ban. Ez az elmélet a kvantummechanika elvei és a speciális relativitás kombinációjaként jött létre, beépítve magába a Maxwell-egyenleteket és egy, Diractól származó, az elektronok mozgását és spinjét szabályozó alapegyenletet. Az elmélet egészében véve nem rendelkezik a korábbi SZUPER elméletek kényszerítő eleganciájával vagy következetességével, de valóban tüneményes pontossága alapján ebbe az osztályba sorolható. Egyik különösen nevezetes eredménye az elektron mágneses momentumának értéke. (Az elektronok a pörgő elektromos töltések pici mágneseihez hasonlóan viselkednek. A mágneses momentum kifejezés e piciny mágnes erősségére vonatkozik.) A QED-ből erre az 1,001 159 652 46 érték jön ki (megfelelő egységekben – az utolsó két jegyben kb. 20 megengedett hibával), míg a legújabb kísérleti érték 1,001 159 652 193 (a lehetséges hiba kb. 10 az utolsó két jegyben). Az ilyen fokú pontosság, amint arra Feynman rámutatott, a New York és Los Angeles közötti távolságot egy emberi hajszál szélességénél kisebb megengedett eltéréssel határozná meg! Az elmélet ismeretére nem lesz szükségünk, de a teljesség kedvéért néhány lényeges vonását a következő fejezet végén vázlatosan megemlítem.68Vannak olyan forgalomban lévő elméletek, amelyeket a HASZNOS osztályba sorolok. Kettőre ezek közül nem lesz szükségünk, de a megemlítést megérdemlik. Az egyik a hadronoknak nevezett szubatomi részecskék (az atommagot felépítő protonok, neutronok, mezonok stb. – vagy pontosabban az erősen kölcsönható részecskék) Gell-Mann–Zweig-féle kvarkmodellje és e részecskék kölcsönhatásainak (később kidolgozott) részletes elmélete, amely kvantumszín-dinamika vagy QCD néven ismert. Az elképzelés az, hogy minden hadron kvarkoknak nevezett összetevőkből épül fel, amelyek egymással a Maxwell-elmélet egy bizonyos általánosítása (az ún. „Yang–Mills-elmélet”) szerint hatnak kölcsön. A másik egy olyan (Glashow, Salam, Ward és Weinberg által kidolgozott – és újra a Yang–Mills-elméletet használó) elmélet, amely az elektromágneses erőket a radioaktív bomlásokért felelős „gyenge” kölcsönhatásokkal házasítja össze. Ez az elmélet tartalmazza az ún. leptonok (elektronok, müonok, neutrinók, W- és Z-részecskék – a „gyengén kölcsönható” részecskék) leírását. Mindkét elméletnek vannak jó kísérleti bizonyítékai. Ám különböző okokból sokkal rendetlenebbek, mint azt szeretnénk (a QED is ilyen, de ezek még inkább), és megfigyelt pontosságuk és jósoló erejük messze nem éri el azt a mértéket, ami a SZUPER osztályba soroláshoz szükséges volna. E két elméletet együttesen (a másodikba beleértve a QED-t) gyakran emlegetik standard modellként.Végül van egy más típusú elmélet, amely, én azt hiszem, legalábbis a HASZNOS osztályba tartozik. Ez a világegyetem eredetének elmélete, amelyet ősrobbanás-elméletnek (Nagy Bummnak) neveznek.69 Ez az elmélet fontos szerepet kap majd a 7. és 8. fejezet fejtegetéseiben.Nem gondolom azt, hogy semmi más nem kerülhet a HASZNOS osztályba.70 Van sok már régebben (vagy legújabban) közkedvelt elképzelés. Mondok néhány nevet: „Kaluza–Klein-elméletek”, „szuperszimmetria” (vagy „szupergravitáció”) és a „GUT”-elméletekhez (és bizonyos belőlük származtatott elképzelésekhez, például az „inflatorikus forgatókönyvhöz”, vö. 153. jegyzet) csatlakozó, rendkívül divatos „húr” (vagy „szuperhúr”) elméletek. Véleményem szerint mindezek határozottan a KÍSÉRLETI osztályban vannak. (Lásd Barrow 1988, Close 1983, Davies és Brown 1988, Squires 1985.) A HASZNOS és KÍSÉRLETI osztályok közötti lényeges különbség a jelentős kísérleti megalapozás hiánya az utóbbiba tartozó elméleteknél.71 Nem mondom ezzel azt, hogy némelyikük esetleg nem emelkedhet fel drámaian a HASZNOS, sőt a SZUPER osztályba. Egyesek valóban ígéretes, eredeti elképzeléseket tartalmaznak, de kísérleti alátámasztás nélkül ezek csak elképzelések maradnak. A KÍSÉRLETI osztály nagyon széles. Az itt fellelhető egyes elképzelések bőven tartalmazhatják a megértés lényeges előrehaladásának csíráit, míg mások szembeötlően félresikerültek, mesterkéltek. (Szándékomban állt egy negyediket lehasítani a tiszteletre méltó KÍSÉRLETI osztályból, és mondjuk a FÉLRESIKERÜLT címkével ellátni – de azután meggondoltam magam, mert nem akartam elveszíteni barátaim felét!)Nem kell meglepődnünk azon, hogy a fő SZUPER elméletek régiek. A történelem során biztosan sokkal-sokkal több elmélet volt, amely a KÍSÉRLETI osztályba került volna, de a legtöbbjük sorsa a feledés lett. Hasonlóképpen a HASZNOS osztályban is sok kellett legyen, amelyek azóta eltűntek; de vannak olyanok is, amelyek beolvadtak másokba, amelyek később SZUPER-rá váltak. Nézzünk néhány példát. Mielőtt Kopernikusz, Kepler és Newton sokkal jobb rendszerüket megalkották, volt a bolygómozgásnak egy csodálatosan kidolgozott elmélete, amelyet a régi görögök gondoltak ki, és a ptolemaioszi rendszer néven volt ismert. E rendszer szerint a bolygók mozgása körmozgások bonyolult összegződése révén alakul ki. Egész jól lehetett vele jóslatokat gyártani, de amint nagyobb pontosságra volt szükség, úgy vált egyre bonyolultabbá. Ma a ptolemaioszi rendszer nagyon mesterkéltnek látszik. Jó példája volt ez a HASZNOS elméletnek (vagy húsz évszázaddal ezelőtt!), amely mint fizikai elmélet később teljesen eltűnt, bár tudománytörténeti szerepe vitathatatlan. A végül sikeres HASZNOS elméleteknek az előbbi helyett jó példája Kepler ragyogó elgondolása a bolygók elliptikus mozgásáról. Egy másik példa a kémiai elemek Mengyelejev-féle periódusos rendszere. Önmagukban ezek nem rendelkeztek a megkövetelt „rendkívüli” jósoló erővel, de a későbbiekben „helyes” következtetésekké váltak azokon a SZUPER elméleteken belül, amelyek belőlük nőttek ki (a newtoni dinamika és a kvantumelmélet).Az elkövetkező szakaszokban és fejezetekben nem kell majd sokat mondanom a forgalomban lévő, csupán HASZNOS vagy KÍSÉRLETI elméletekről.
Elég, ha azokról beszélünk, amelyek SZUPER-ek. Valóban szerencsés dolog, hogy vannak ilyen elméleteink, és hogy ilyen figyelemreméltó teljességgel meg tudjuk érteni a világot, amelyben élünk. Végül meg kell próbálnunk majd eldönteni, elég gazdagok-e ezek az elméletek, hogy kormányozzák agyunk és értelmünk működését. A megfelelő helyen erre a kérdésre majd visszatérek; most azonban nézzük meg a SZUPER elméleteket mai formájukban, és próbáljunk eltöprengeni, milyen jelentőségük lehet céljaink szempontjából.
- SZUPER,
- HASZNOS,
- KÍSÉRLETI.
Euklideszi geometria
Az euklideszi geometria az a tárgykör, amelyet az iskolában „geometria” néven tanulunk. Azt hiszem azonban, hogy a legtöbb ember inkább matematikának gondolja, mintsem fizikai elméletnek. Matematika is természetesen, de semmi esetre sem az egyetlen elképzelhető matematikai geometria. E speciális geometria, amelyet Eukleidész hagyott ránk, nagyon pontosan leírja a világunk fizikai terét, amelyben élünk, de ez nem logikai szükségszerűség – csak éppen a fizikai világ egy (majdnem egzakt) megfigyelt tulajdonsága.Valóban van egy másik, a Bolyai–Lobacsevszkij-féle (vagy hiperbolikus) geometria,72 amely a legtöbb tekintetben nagyon hasonló az euklideszihez, de vannak bizonyos érdekes különbségek. Emlékezzünk például arra, hogy az euklideszi geometriában minden háromszög szögeinek összege 180°. A Bolyai–Lobacsevszkij-geometriában ez az összeg mindig kevesebb, mint 180°, a különbség arányos a háromszög területével (lásd az 5.1. ábrát).
Nagyon könnyen előfordulhat, hogy a Bolyai–Lobacsevszkij-geometria kozmikus skálán érvényes világunkra (lásd 7. fejezet). Azonban a háromszög szöghiánya és területe közötti arányossági tényező ebben az esetben rendkívül kicsi kellene legyen, és az euklideszi geometria bármilyen közönséges skálán kitűnő közelítése volna ennek a geometriának. Einstein általános relativitáselmélete, mint e fejezetben később látni fogjuk, valójában azt mondja nekünk, hogy világunk geometriája a kozmológiainál sokkal kisebb skálákon eltér az euklideszitől (noha olyan „szabálytalan” módon, ami sokkal bonyolultabb a Bolyai–Lobacsevszkij-geometriánál), bár közvetlen tapasztalataink közönséges skáláján az eltérések még mindig nagyon kicsik.
Távol attól, hogy logikai szükségszerűség legyen, tapasztalatilag megfigyelt tény az, hogy az euklideszi geometria olyan pontosan – ha nem is teljesen egzaktul – illik fizikai terünk szerkezetére! Az euklideszi geometria valójában mindvégig (SZUPER) fizikai elmélet volt azon felül, hogy a tiszta matematika elegáns és logikus darabja.Bizonyos értelemben nincs nagyon messze ez a Platón által kedvelt filozófiai nézőponttól (i. e. 360 körül; úgy ötven évvel Eukleidész Elemek című, a geometriáról szóló könyve előtt). Platónnál a tiszta geometria tárgyai – egyenes vonalak, körök, háromszögek, síkok stb. – csak közelítőleg valósulnak meg az igazi fizikai dolgok világában. A tiszta geometriának ezek a matematikailag pontos tárgyai egy másik világot népesítenek be, a matematikai fogalmak platóni ideális világát. Platón világa nem tapintható tárgyakat tartalmaz, hanem matematikai dolgokat. Ez a világ számunkra nem a megszokott fizikai módon érhető el, hanem az értelem útján. Eszünk mindig akkor lép érintkezésbe Platón világával, amikor a matematikai gondolkodás és meglátás gyakorlatával felfog egy matematikai igazságot. Ezt az idealizált világot különállónak tekintették és tökéletesebbnek külső tapasztalásaink anyagi világánál, de éppen olyan valódinak. (Emlékezzünk vissza fejtegetéseinkre a matematikai fogalmak platóni valóságáról a 3. és 4. fejezetekben.) Így amíg a tiszta euklideszi geometria tárgyait gondolatban lehet tanulmányozni, és ezáltal le lehet vezetni az ideális világ sok tulajdonságát, az nem szükségszerű, hogy a külső tapasztalás tökéletlen fizikai világa pontosan tapadjon ehhez az ideális világhoz. Úgy látszik, hogy valamilyen varázslatos meglátás révén és a saját idejében minden bizonnyal nagyon szórványos bizonyítékok alapján Platón előre látta, hogy: egyrészt a matematikát önmagáért kell tanulmányozni és megérteni, és nem kell megkövetelni, hogy teljesen pontosan alkalmazható legyen a fizikai tapasztalat tárgyaira; másrészt a valóságos, külső világot végül is csak a precíz matematika alapján lehet megérteni – azaz Platón az értelem útján elérhető ideális világa alapján!Most azonban az Akadémia egy másik tagjával fogunk foglalkozni – aki valamivel kevésbé ismert, mint Arisztotelész, de szerintem sokkal finomabb tudós –, az ókor egyik nagy gondolkodójával, a matematikus és csillagász Eudoxosszal.Az euklideszi geometriának van egy mély és finom tartozéka – valójában az egyik leglényegesebb –, amit manapság aligha gondolnánk geometriának! (A matematikusok inkább „analízisnek” neveznék, mint „geometriának”.) Ez a tartozék a valós számok bevezetése. Az euklideszi geometria távolságokra és szögekre vonatkozik. Hogy e geometriát megértsük, fel kell fognunk, milyen típusú számokra van szükség a távolságok és szögek leírásához. A központi új elképzelést Eudoxosz (kb. i. e. 408–355) vetette fel a 4. században időszámításunk előtt.73 A görög geometria „krízist” élt át a pitagoreusok azon felfedezése következtében, hogy az olyan számok, mint a (amelyre azért van szükség, hogy a négyzet átlóját kifejezhessük az oldal hosszával), nem írhatók fel törtként (vö. 3. fejezet). A görögök számára fontos volt, hogy a geometriai méreteket (arányokat) ki tudják fejezni egészekkel (egészek hányadosaival), mert így a geometriai nagyságokat az aritmetika törvényei szerint tudták tanulmányozni.Penrose nem nagyon kedveli a szellem világával szemben az anyagi világ elsődlegességét hirdetőket. Lám "szegény" Arisztotelész nem eléggé finom tudós szerinte...Hozzám, aki inkább a két világ határánszeret bóklászni Arisztotelész és az általa képviselt irány közelebb áll, Platon világa viszont nagyon költői, messzelebegő fátyol, csillagköd az "éterben". Úgyhogy: pro primo, pro secondo, de a kettő együtt az egész. Van azonban egy lényeges különbség Eudoxosz, illetve Dedekind és Weierstrass javaslatai között. Az ókori görögök úgy gondoltak a valós számokra, mint adott dolgokra – geometriai méretekkel (azok arányaival) kifejezve –, azaz a „valóságos” tér tulajdonságaira. Számukra szükséges volt, hogy a geometriai méreteket az aritmetikával tudják kezelni, hogy szigorúan tudjanak beszélni róluk, és összegeikről és szorzataikról is – lényeges összetevői ezek az ókoriak oly sok csodálatos geometriai tételének. (Az 5.3. ábrán illusztrációként bemutatom a nevezetes Ptolemaiosz-tételt – bár Ptolemaiosz Eudoxosz koránál jóval később fedezte azt fel – egy körön lévő négy pont közötti távolságok kapcsolatáról, amely szépen mutatja, hogy az összegekre és szorzatokra is szükség van.) Eudoxosz feltételei rendkívül gyümölcsözőknek bizonyultak, például ezek tették lehetővé a görögök számára a területek és térfogatok szabatos számítását.
Azonban a 19. század matematikusai számára – és valójában a maiak számára is – megváltozott a geometria szerepe. Az ókori görögöknek és különösen Eudoxosznak a „valós” számok olyan dolgok voltak, amelyeket a fizikai tér geometriájából kellett „kihámozniuk”. Ma jobban szeretünk úgy gondolni a valós számokra, mint amelyek a geometriánál logikailag primitívebbek. Ez teszi lehetővé számunkra, hogy felépítsük a különböző típusú geometriák minden fajtáját, mindegyiket a szám fogalmából kiindulva. (Az alapeszme a koordinátageometria, amit a 17. században vezetett be Fermat és Descartes. A koordináták felhasználhatók más típusú geometriák definiálására.) Bármelyik ilyen „geometria” logikailag konzisztens kell legyen, de nem kell, hogy közvetlenül kapcsolódjék tapasztalataink fizikai teréhez. Az a speciális fizikai geometria, amelyet látszólag érzékelünk, a tapasztalat egy idealizációja (függ például attól, hogyan extrapolálunk a végtelenül nagy vagy kicsi méretekhez, vö. 3. fejezet), de a kísérletek ma elég pontosak ahhoz, hogy fel kelljen fognunk, „tapasztalt” geometriánk valóban különbözik az euklideszi ideálistól, és összhangban van azzal, amit Einstein általános relativitáselmélete mond. Ám a fizikai világ geometriájáról alkotott nézetünk változásai ellenére Eudoxosz 23 évszázados valósszám-fogalma lényegében változatlan maradt, és Einstein elméletének éppen olyan lényeges összetevője, mint Eukleidészének. Valójában minden eddigi komoly fizikai elméletnek lényeges alkotórésze!Eukleidész Elemekjének ötödik könyve alapjában az Eudoxosz által bevezetett és az előbb leírt „arányosságelmélet” kifejtése. Ez alapvetően fontos volt a mű egésze számára. Az először i. e. 300 körül kiadott teljes Elemeket valóban úgy kell értékelnünk, mint minden idők egyik legmélyebb hatású könyvét. Ez a mű teremtette meg majdnem minden későbbi tudományos és matematikai gondolkodás színpadát. Módszerei deduktívak voltak, világosan felállított axiómákból indultak ki, amelyekről feltételezte, hogy a tér „magától értetődő” tulajdonságai; és számos következményt vezetett le, közülük sok a meglepő és fontos és egyáltalán nem magától értetődő. Nem vitás, hogy Eukleidész műve mély hatást gyakorolt a tudományos gondolkodás elkövetkező fejlődésére.
-------------------------------------------------------------------------------------------------------------------- ----------------------------------Galilei és Newton dinamikája
 Newton meg tudta mutatni, hogy Kepler három törvénye következik az ő általános rendszeréből (inverz négyzetes vonzási erőtörvény mellett). Ezen kívül megkapott minden részletes korrekciót Kepler ellipszispályáihoz, és más jelenségeket is, mint például a napéjegyenlőség precesszióját (a Föld forgástengelye irányának lassú mozgását, amelyet a görögök az évszázadok során megfigyeltek). Hogy mindezeket elérje, Newtonnak – a differenciálszámítás mellett – sok matematikai technikát kellett kidolgoznia. Erőfeszítéseinek tüneményes sikerét nagyban köszönhette kiemelkedő matematikai ügyességének és nem kevésbé nagyszerű fizikai meglátásainak.
Newton meg tudta mutatni, hogy Kepler három törvénye következik az ő általános rendszeréből (inverz négyzetes vonzási erőtörvény mellett). Ezen kívül megkapott minden részletes korrekciót Kepler ellipszispályáihoz, és más jelenségeket is, mint például a napéjegyenlőség precesszióját (a Föld forgástengelye irányának lassú mozgását, amelyet a görögök az évszázadok során megfigyeltek). Hogy mindezeket elérje, Newtonnak – a differenciálszámítás mellett – sok matematikai technikát kellett kidolgoznia. Erőfeszítéseinek tüneményes sikerét nagyban köszönhette kiemelkedő matematikai ügyességének és nem kevésbé nagyszerű fizikai meglátásainak.Kiszámítható-e az élet a biliárdgolyó-világban?
Bármelyik determinisztikus fizikai elméletről megkérdezhetjük, hogy kiszámítható-e vagy sem. Valóban, kiszámítható-e a newtoni biliárdgolyó-világ?
A fizikai kiszámíthatóság kérdése részben attól függ, milyen kérdéseket akarunk a rendszernek feltenni. Van azonban olyan értelmezés, amelyben e világ a gyakorlatban „nem kiszámítható”. Ez abból a körülményből ered, hogy mindig korlátozott az a pontosság, amellyel a kezdeti adatokat ismerni lehet. Ténylegesen nagyon jelentős „instabilitás” van inherensen jelen az ilyen típusú problémában. Nagyon pici változás a kezdeti adatokban gyorsan roppant nagy változást idézhet elő az eredő viselkedésben. Az ilyen típusú instabilitásra gyakran használják a „káosz” vagy „kaotikus viselkedés” kifejezéseket. Fontos a kaotikus viselkedés például az időjárásban. Noha az elemeket kormányzó Newton-egyenletek jól ismertek, a hosszú távú időjárási előrejelzések közismerten megbízhatatlanok!Ez egyáltalán nem az a fajta „nemkiszámíthatóság”, amelyet bármilyen módon „ki lehet aknázni”. Csupán annyiról van szó, hogy mert a kezdeti állapot csak korlátozott pontossággal ismerhető, a jövőbeli állapot a kezdetiből nem kiszámítható megbízhatóan. Valójában egy „véletlenszerű elem” kerül be a jövőbeli viselkedésbe, de ennyi az egész. Ha az agy valóban hasznos nem kiszámítható elemeket aknáz ki a fizikai törvényekben, akkor ezeknek a fentitől egészen különbözőeknek és sokkal pozitívabbaknak kell lenniük. Ennek megfelelően erre a fajta „kaotikus” viselkedésre egyáltalán nem fogom használni a „nem kiszámítható” kifejezést, inkább a „jósolhatatlant”. A jósolhatatlanság jelenléte nagyon általános jelenség az olyan jellegű determinisztikus törvényekben, amelyek a (klasszikus) fizikában ténylegesen fellépnek, ezt hamarosan látni fogjuk. A jósolhatatlanság biztosan olyan dolog, amelyet egy gondolkodó gép készítése során minimalizálni szeretnénk, nem pedig „kiaknázni”!
Hamiltoni mechanika
A newtoni mechanika sikereit nemcsak az eredményezte, hogy nagyszerűen alkalmazható a fizikai világra, hanem a belőle kinövő matematikai elmélet gazdagsága is. Figyelemre méltó, hogy a Természet minden SZUPER elmélete a matematikai ideák rendkívül termékeny forrásának bizonyult. Mély és szép titok van abban a tényben, hogy e szuperpontos elméletek mint egyszerű matematika is rendkívül gyümölcsözőek. Ez kétségtelenül mond valami mélyet nekünk a fizikai tapasztalataink valóságos világa és a matematika platóni világa közötti kapcsolatokról. (E kérdést később fogom tárgyalni a 10. fejezetben.) A newtoni mechanika talán a legfontosabb ebben a vonatkozásban, mert születése hozta meg az analízist. Mi több, a speciális newtoni rendszer a matematikai gondolatok nevezetes gyűjteményét teremtette meg, azt, amelyet klasszikus mechanika néven ismerünk. Fejlődéséhez hozzájárult a tizennyolcadik és tizenkilencedik század sok nagy matematikusa: Euler, Lagrange, Laplace, Liouville, Poisson, Jacobi, Osztrogradszkij, Hamilton. E munka nagy részét foglalja magában az, amit „Hamilton-elméletnek”81 nevezünk. A hamiltoni rendszer egyik újszerű vonása a fizikai rendszer leírására használt „változókban” van. Mindeddig a részecskék helyzetét tekintettük elsődlegesnek, a sebesség egyszerűen a helyzetváltoztatás időbeli nagysága volt. Emlékezzünk rá, hogy egy newtoni rendszer kezdeti állapotának megadásához szükségünk volt minden részecske helyzetére és sebességére, hogy az ezután következő viselkedés meghatározott legyen. A hamiltoni megfogalmazásban a részecskéknek nem sebességeit, hanem impulzusait kell kiválasztanunk. (Korábban megjegyeztük, hogy egy részecske impulzusa a sebességének és a tömegének szorzata.) Ez önmagában kis változásnak tűnhet, a fontos azonban az, hogy úgy kezeljük minden részecske helyét és impulzusát, mint többé-kevésbé egyenrangú, független mennyiségeket.A Hamilton-formalizmus a mechanika nagyon elegáns, szimmetrikus leírását nyújtja. Hogy éppen csak lássuk, hogyan néznek ki, írjuk le itt az egyenleteket, még ha sok Olvasó nincs is hozzászokva az analízis jelöléseihez, amely szükséges a teljes megértéshez – most azonban nem lényeges a teljes megértés. Amit a differenciálszámításról igazán fel kell fogni, az annyi, hogy az egyenletek bal oldalán megjelenő „pont” az időbeli változás sebességét jelöli (az impulzusét az első egyenletben, a helyét a másodikban): Itt az i indexet a különböző p1, p2, p3, p4, … impulzus- és x1, x2, x3, x4, … helykoordináták megkülönböztetésére használjuk. n szabad részecske esetén 3n impulzuskoordinátánk és 3n helykoordinátánk lesz (a három független térbeli irány mindegyikéhez egy). A ∂ szimbólum a „parciális differenciálás” jele („az olyan differenciálásé, amikor minden más változót állandónak tartunk”), H pedig az előbb leírt Hamilton-függvény. Az x1, x2, … és pl, p2, … koordináták valójában sokkal általánosabb dolgok lehetnek, mint a részecskék közönséges Descartes-koordinátái (azaz az xi-k a közönséges távolságok három egymásra merőleges irányban mérve). Egyes xi koordináták lehetnek például szögek (amikor is a megfelelő pi-k impulzusmomentumok, és nem impulzusok), vagy valamilyen más, egészen általános mértékek. Figyelemre méltó, hogy a Hamilton-egyenletek pontosan ugyanolyan alakúak maradnak. Valójában H alkalmas megválasztásával a Hamilton-egyenletek érvényesek maradnak bármilyen klasszikus egyenletrendszerre, nem csak a Newton-egyenletekre. Fennáll ez a Maxwell(–Lorentz)-elméletre is, amelyet rövidesen megvizsgálunk. A Hamilton-egyenletek érvényesek a speciális relativitáselméletben is. Megfelelő gondossággal még az általános relativitáselmélet is beilleszthető a hamiltoni keretbe. Továbbá, ahogy azt később a Schrödinger-egyenletnél látni fogjuk (6. fejezet), ez a hamiltoni keret szolgáltatja az összehasonlító pontot a kvantummechanika egyenletei számára. Igazán figyelemreméltó, hogy bár a fizikai elméletek a múlt században és azután forradalmi változásokon mentek keresztül, a dinamikai egyenletek szerkezetében ilyen formai egység mutatkozik!
Fázistér
A Hamilton-egyenletek alakja lehetővé teszi, hogy nagyon hatásos és általános módon jelenítsük meg egy klasszikus rendszer fejlődését. Próbáljunk elképzelni egy nagy dimenziószámú „teret”, minden x1, x2, …, p1, p2, … koordinátához tartozzék egy dimenzió. (Matematikai tereknek gyakran van háromnál több dimenziójuk.) Ennek a térnek a neve fázistér (lásd 5.10. ábra), n szabad részecske esetén 6n a dimenziószáma (minden részecskéhez három hely- és három impulzuskoordináta tartozik). Az Olvasó joggal aggódhat, hogy ez már egyetlen részecskénél is kétszer annyi dimenzió, mint amennyit a megjelenítésre rendesen használni szokott! A dolog titka az, hogy nem szabad megijedni. Noha hat dimenzió valóban több, mint amennyit könnyen(!) lehet ábrázolni, valójában nem is volna sok haszna annak, ha képesek volnánk ábrázolni. Egy levegőmolekulákkal teli szoba olyan rendszer, amelynél a fázistér dimenzióinak száma 10 000 000 000 000 000 000 000 000 000
körüli lehet. Ilyen nagy tér pontos megjelenítését megpróbálni nem sok reménnyel kecsegtet! A trükk az, hogy meg se próbáljuk – még egyetlen részecske fázisterét sem. Csak gondoljunk el valami homályos háromdimenziós (sőt kétdimenziós) tartományra. Vessünk egy pillantást az 5.10. ábrára. Ez teljesen kielégítő lesz.
A fázistérbeli szétszóródásnak van egy másik nevezetes vonzata. Valójában azt mondja, hogy a klasszikus mechanika nem lehet érvényes világunkra! E következményt valamennyire eltúloztam, de talán nem olyan nagyon. A klasszikus mechanika jól számot tud adni a folyékony testek viselkedéséről – különösen a gázokéról, de a folyadékokéról is elég jól –, ahol a részecskerendszereknek csak „átlagolt” tulajdonságaival törődünk, de nehézségei vannak a szilárd testek szerkezetével kapcsolatban, ahol részletesebb rendezett szerkezetre van szükség. Probléma az, hogyan tarthatja meg alakját egy szilárd test, mikor pontszerű részecskék miriádjaiból áll össze, amelyek szervezett elrendezése a fázistérbeli szétszóródás miatt folyamatosan gyengül. Ma már tudjuk, a kvantumelméletre van szükség ahhoz, hogy a szilárd testek tényleges szerkezetét megfelelően megérthessük. A kvantumos jelenségek valahogyan meg tudják akadályozni ezt a fázistérbeli szétszóródást. A kérdés fontos, később majd vissza kell rá térnünk (lásd a 8. és 9. fejezetet).
A probléma a „számítógép-készítés” kérdésében is lényeges. A fázistérbeli szétfolyás olyan dolog, amit ellenőrzés alatt kell tartani. Nem engedhető meg, hogy egy számítóeszköz „diszkrét” állapotának megfelelő fázistértartomány (mint az előbbiekben leírt R0) túlságosan szétfolyjék. Emlékezzünk vissza, hogy még a Fredkin–Toffoli-féle „biliárdgolyó-számítógépnek” is különálló, szilárd falakra van szüksége, hogy működni tudjon. Egy sok részecskéből összetevődő tárgy „szilárdságának” a működési feltétele a kvantummechanika. Úgy látszik, hogy még egy „klasszikus” számítómasinának is kölcsönöznie kell a kvantumfizika jelenségeiből, hogy hatékonyan működjék!
A probléma a „számítógép-készítés” kérdésében is lényeges. A fázistérbeli szétfolyás olyan dolog, amit ellenőrzés alatt kell tartani. Nem engedhető meg, hogy egy számítóeszköz „diszkrét” állapotának megfelelő fázistértartomány (mint az előbbiekben leírt R0) túlságosan szétfolyjék. Emlékezzünk vissza, hogy még a Fredkin–Toffoli-féle „biliárdgolyó-számítógépnek” is különálló, szilárd falakra van szüksége, hogy működni tudjon. Egy sok részecskéből összetevődő tárgy „szilárdságának” a működési feltétele a kvantummechanika. Úgy látszik, hogy még egy „klasszikus” számítómasinának is kölcsönöznie kell a kvantumfizika jelenségeiből, hogy hatékonyan működjék!
Maxwell elektromágneses elmélete
A világ newtoni képében piciny részecskékre gondolunk, ezek egymásra a közöttük lévő távolságtól függő erővel hatnak – ha pedig nem teljesen pontszerűek, akkor alkalmanként, a tényleges fizikai érintkezéskor visszapattannak egymásról. Mint már előbb említettem, az elektromos és mágneses erők (mindkettő létezéséről az ókor óta tudnak, részletesebben William Gilbert 1600-ban és Benjamin Franklin 1752-ben kezdte tanulmányozni azokat) a gravitációs erőkhöz hasonlóan hatnak, amennyiben szintén a távolság négyzetével fordított arányban csökkennek, viszont inkább taszítóak, mint vonzóak – azaz hasonló a hasonlót taszítja –, és nem a tömeg, hanem az elektromos töltés (illetve a mágneses pólus erőssége) szabja meg az erő nagyságát. Ezen a szinten az elektromosság és a mágnesség nehézség nélkül beilleszthető a newtoni sémába. A fény viselkedése nagyjából (bár némi határozott nehézséggel) szintén leírható vagy úgy, hogy egyedi részecskékből (fotonokból, ahogy ma mondjuk) összeállónak tekintjük, vagy hullámmozgásnak valamilyen közegben, ez utóbbi esetben magát a közeget („étert”) is részecskékből állónak kell gondolnunk.
A világ newtoni képében piciny részecskékre gondolunk, ezek egymásra a közöttük lévő távolságtól függő erővel hatnak – ha pedig nem teljesen pontszerűek, akkor alkalmanként, a tényleges fizikai érintkezéskor visszapattannak egymásról. Mint már előbb említettem, az elektromos és mágneses erők (mindkettő létezéséről az ókor óta tudnak, részletesebben William Gilbert 1600-ban és Benjamin Franklin 1752-ben kezdte tanulmányozni azokat) a gravitációs erőkhöz hasonlóan hatnak, amennyiben szintén a távolság négyzetével fordított arányban csökkennek, viszont inkább taszítóak, mint vonzóak – azaz hasonló a hasonlót taszítja –, és nem a tömeg, hanem az elektromos töltés (illetve a mágneses pólus erőssége) szabja meg az erő nagyságát. Ezen a szinten az elektromosság és a mágnesség nehézség nélkül beilleszthető a newtoni sémába. A fény viselkedése nagyjából (bár némi határozott nehézséggel) szintén leírható vagy úgy, hogy egyedi részecskékből (fotonokból, ahogy ma mondjuk) összeállónak tekintjük, vagy hullámmozgásnak valamilyen közegben, ez utóbbi esetben magát a közeget („étert”) is részecskékből állónak kell gondolnunk.
Tekintsünk először egy mágneses mezőt! A legtöbb Olvasó már látta, hogyan viselkedik a vasreszelék, ha olyan papírra szórjuk, amely alatt mágnes van. A vasreszelék meglepő módon felsorakozik az ún. „mágneses erővonalak” mentén. Úgy képzeljük, hogy az erővonalak akkor is ott maradnak, amikor a vasreszelék nincs ott. Ezek képezik azt, amit mágneses mezőnek nevezünk. Ez a „mező” a tér minden pontjában egy bizonyos irányba mutat, nevezetesen az erővonalak irányába. Ténylegesen egy vektorunk van minden pontban, így a mágneses mező a vektormezőknek egy példája. (Összehasonlíthatnánk a hamiltoni vektormezővel, amelyről az előző szakaszban volt szó, de ez a vektormező most a közönséges térben van, nem a fázistérben.) Hasonlóképpen, egy elektromosan töltött testet egy másfajta mező, az elektromos mező vesz körül, és minden tömeges testet hasonlóan egy gravitációs mező. Ezek is vektormezők a térben.
Ilyen elképzelések már régen Faraday előtt ismertek voltak, és az elméletiek fegyvertárának nagyon komoly részévé váltak a newtoni mechanikában. Azonban az uralkodó nézőpont az ilyen „mezőket” nem tekintette valódi fizikai szubsztanciának. Inkább úgy gondolták, hogy ezekkel lehet „számon tartani” az erőket, amelyek hatnának, ha egy megfelelő részecskét helyeznének a különböző pontokba. Faradayt azonban alapvető kísérleti felfedezései (mozgó tekercsekkel, mágnesekkel és hasonlókkal) arra vezették, hogy az elektromos és mágneses mezőket „valóságos” fizikai anyagnak higgye, sőt mi több, úgy gondolta, hogy a változó elektromos és mágneses mezők olykor képesek egymást az egyébként üres téren „keresztültolni”, így hoznak létre egyfajta testetlen hullámot! Feltételezte, hogy a fény maga is ilyen hullámokból állhat. Ez a nézet eltért az uralkodó „newtoni bölcsességtől”, amelyben az ilyen mezőket semmilyen értelemben nem gondolták „valóságosaknak”, csak kényelmes matematikai segédeszközöknek a „valóság” „igazi” newtoni pontrészecske-távolhatás képéhez.
Ilyen elképzelések már régen Faraday előtt ismertek voltak, és az elméletiek fegyvertárának nagyon komoly részévé váltak a newtoni mechanikában. Azonban az uralkodó nézőpont az ilyen „mezőket” nem tekintette valódi fizikai szubsztanciának. Inkább úgy gondolták, hogy ezekkel lehet „számon tartani” az erőket, amelyek hatnának, ha egy megfelelő részecskét helyeznének a különböző pontokba. Faradayt azonban alapvető kísérleti felfedezései (mozgó tekercsekkel, mágnesekkel és hasonlókkal) arra vezették, hogy az elektromos és mágneses mezőket „valóságos” fizikai anyagnak higgye, sőt mi több, úgy gondolta, hogy a változó elektromos és mágneses mezők olykor képesek egymást az egyébként üres téren „keresztültolni”, így hoznak létre egyfajta testetlen hullámot! Feltételezte, hogy a fény maga is ilyen hullámokból állhat. Ez a nézet eltért az uralkodó „newtoni bölcsességtől”, amelyben az ilyen mezőket semmilyen értelemben nem gondolták „valóságosaknak”, csak kényelmes matematikai segédeszközöknek a „valóság” „igazi” newtoni pontrészecske-távolhatás képéhez.
Szembetalálva magát Faraday kísérleti felfedezéseivel, meg a neves francia fizikus, André Marie Ampère (1775–1836) és mások korábbi eredményeivel és megihletve Faraday látomása által James Clerk Maxwell (1831–1879), a nagy skót fizikus és matematikus, eltűnődött az elektromos és mágneses mezőkre vonatkozó egyenletek matematikai alakján. Figyelemre méltó meglátással változtatást javasolt az egyenletekben – látszólag talán eléggé csekélyet, de következményeit tekintve alapvetőt. E változtatást egyáltalán nem az ismert kísérleti tények sugallták (bár azokkal összhangban volt), Maxwell saját elméleti, részben fizikai, részben matematikai és részben esztétikai követelményeinek eredménye volt. A Maxwell-egyenletek egyik következménye, hogy az elektromos és mágneses mezők valóban „tolják” egymást az üres téren keresztül. Egy oszcilláló mágneses mező oszcilláló elektromos mezőt kelt (ezt Faraday kísérleti felfedezése sugallta), ez az oszcilláló elektromos mező viszont oszcilláló mágneses mezőt (ami Maxwell elméleti következtetése), ez újra elektromos mezőt és így tovább. (Az ilyen hullámok részletes képét illetően lásd a 6.26., 6.27. ábrákat.) Maxwell ki tudta számítani, milyen sebességgel terjed e hatás a térben – és azt találta, hogy ez a fény sebessége! Ezek az ún. elektromágneses hullámok mutatják továbbá az interferenciát és a fény rejtélyes polarizációs tulajdonságait, amelyeket már régóta ismertek (ezekkel a 6. fejezetben fogunk találkozni). Amellett, hogy számot adott a látható fény tulajdonságairól, amikor a hullámhossz egy meghatározott tartományba esik (4 – 7 ∙ 10–7 m), más hullámhosszú elektromágneses hullámokat is megjósolt, amelyeket huzalban folyó elektromos áram kelt. E hullámok létezését kísérletileg a híres német fizikus, Heinrich Hertz mutatta ki 1888-ban. Faraday ihletett reménysége valóban szilárd alapra lelt a csodálatos Maxwell-egyenletekben! ... 
Itt E, B és j rendre az elektromos mezőt, a mágneses mezőt és az elektromos áramot leíró vektormezők; ρ az elektromos töltéssűrűség, c pedig egy állandó, a fény sebessége.84 A „rot” és „div” jelölésekkel ne törődjünk, ezek különböző térbeli változásokra utalnak. (A térkoordináta szerinti parciális differenciálások bizonyos kombinációi. Emlékezzünk vissza a parciális differenciálás ∂ szimbólummal jelölt műveletére, amellyel a Hamilton-egyenleteknél már találkoztunk.) Az első két egyenlet bal oldalán látható ∂/∂t operátor tulajdonképpen ugyanaz, mint a Hamilton-egyenletekben használt „pont”, a különbség csupán technikai. Így ∂E/∂t „az elektromos mező változási sebességét”, ∂B/∂t „a mágneses mező változási sebességét” jelöli. Az első egyenlet85 megmondja, hogyan változik időben az elektromos mező attól függően, mit csinál pillanatnyilag a mágneses mező és az elektromos áram; a második egyenlet azt mondja meg, hogyan változik időben a mágneses mező attól függően, mit csinál pillanatnyilag az elektromos mező. A harmadik egyenlet durván szólva az inverz négyzetes törvény egy rejtett alakja, megmondja, milyen kapcsolatban kell legyen az elektromos mező a pillanatnyi töltéseloszlással; míg a negyedik egyenlet ugyanez lenne a mágneses mezőre, csakhogy „mágneses töltések” (különálló északi vagy déli pólusú részecskék) nincsenek. Ezek az egyenletek annyiban hasonlítanak a Hamilton-egyenletekre, hogy megmondják, mi kell legyen a lényeges mennyiségek (most az elektromos és mágneses mező) időbeli változási sebessége az adott időpontbeli értékeikkel kifejezve. Így a Maxwell-egyenletek éppen úgy determinisztikusak, mint ahogy a közönséges Hamilton-egyenletek. Az egyetlen különbség az – és ez lényeges különbség –, hogy a Maxwell-egyenletek nem részecske-, hanem mezőegyenletek, ami annyit jelent, hogy a rendszer állapotának leírásához végtelen számú paraméterre van szükség (a mező vektorokra a tér minden egyes pontjában), és nem véges számúra, mint a részecskeelméletben (három hely- és három impulzuskoordinátára minden részecskénél). Így a Maxwell-elméletnél a fázistér egy végtelen dimenziószámú tér! (Mint korábban említettem, a Maxwell-egyenleteket ténylegesen be lehet illeszteni az általános hamiltoni keretbe, de ezt a keretet a végtelen dimenzió miatt egy kissé ki kell tágítani.)86 A fizikai valóságról alkotott képünkben, ahogy azt a Maxwell-elmélet mutatja, az előző eseten túlmenően az az alapvetően új alkotórész, hogy most mezőket kell saját jogukon komolyan vennünk, nem lehet ezeket csupán a newtoni elmélet „valódi” részecskéihez tartozó matematikai függeléknek tekintenünk. Maxwell megmutatta, hogy amikor a mezők elektromágneses hullámként terjednek, határozott mennyiségű energiát visznek magukkal. Meg tudta adni ennek az energiának explicit kifejezését. E figyelemre méltó tényt, hogy ezekkel a „testetlen” elektromágneses hullámokkal energiát lehet helyről helyre szállítani, kísérletileg az erősítette meg, hogy Hertz észlelt ilyen hullámokat. Olvasónapló, olyan ez. Magamnak jegyzem, idézem Penrose írását hosszan. Simonyi Károly A Fizika kultúrtörténete c. könyve hasonló olvasmány. 'Olyan unalmas ez a munka, egész nap az irodában ülve, 'mint egy most- fizikapéldákat- fogunk- megoldani óra Gizusnál '- írja Orsi nekem 69 nyarán. Szegény Gizus, szegény Orsi.
Szembetalálva magát Faraday kísérleti felfedezéseivel, meg a neves francia fizikus, André Marie Ampère (1775–1836) és mások korábbi eredményeivel és megihletve Faraday látomása által James Clerk Maxwell (1831–1879), a nagy skót fizikus és matematikus, eltűnődött az elektromos és mágneses mezőkre vonatkozó egyenletek matematikai alakján. Figyelemre méltó meglátással változtatást javasolt az egyenletekben – látszólag talán eléggé csekélyet, de következményeit tekintve alapvetőt. E változtatást egyáltalán nem az ismert kísérleti tények sugallták (bár azokkal összhangban volt), Maxwell saját elméleti, részben fizikai, részben matematikai és részben esztétikai követelményeinek eredménye volt. A Maxwell-egyenletek egyik következménye, hogy az elektromos és mágneses mezők valóban „tolják” egymást az üres téren keresztül. Egy oszcilláló mágneses mező oszcilláló elektromos mezőt kelt (ezt Faraday kísérleti felfedezése sugallta), ez az oszcilláló elektromos mező viszont oszcilláló mágneses mezőt (ami Maxwell elméleti következtetése), ez újra elektromos mezőt és így tovább. (Az ilyen hullámok részletes képét illetően lásd a 6.26., 6.27. ábrákat.) Maxwell ki tudta számítani, milyen sebességgel terjed e hatás a térben – és azt találta, hogy ez a fény sebessége! Ezek az ún. elektromágneses hullámok mutatják továbbá az interferenciát és a fény rejtélyes polarizációs tulajdonságait, amelyeket már régóta ismertek (ezekkel a 6. fejezetben fogunk találkozni). Amellett, hogy számot adott a látható fény tulajdonságairól, amikor a hullámhossz egy meghatározott tartományba esik (4 – 7 ∙ 10–7 m), más hullámhosszú elektromágneses hullámokat is megjósolt, amelyeket huzalban folyó elektromos áram kelt. E hullámok létezését kísérletileg a híres német fizikus, Heinrich Hertz mutatta ki 1888-ban. Faraday ihletett reménysége valóban szilárd alapra lelt a csodálatos Maxwell-egyenletekben! ...
Kiszámíthatóság és a hullámegyenlet
Maxwell egyenleteiből képes volt közvetlenül levezetni, hogy a tér azon tartományaiban, ahol töltések és áramok nincsenek (azaz, ahol j = 0, ρ = 0 a fenti egyenletekben), ott az elektromos és a mágneses mező minden komponensének ki kell elégítenie egy hullámegyenlet néven ismert egyenletet.87 A hullámegyenlet a Maxwell-egyenletek „egyszerűsített változatának” tekinthető, mert egyetlen mennyiségre vonatkozó egyenlet, nem szerepel benne az elektromos és mágneses mezőknek mind a hat komponense. Megoldásai hullámszerű viselkedést mutatnak, s nem rendelkeznek olyanféle járulékos bonyodalmakkal, mint a Maxwell-elmélet „polarizációja” (az elektromos vektormező iránya, lásd 6. fejezet).Marian Boykan Pour-El és Ian Richards (1979, 1981, 1982) meg tudták mutatni, hogy bár a hullámegyenletek megoldásai a szokásos értelemben determinisztikusan viselkednek – azaz egy kezdeti időpontban előírt adatok meghatározzák a megoldást minden más időpontban –, léteznek bizonyos „sajátos” jellegű kiszámítható kezdeti adatok, amelyeknek megvan az a tulajdonságuk, hogy a mező elvileg meghatározott értéke egy későbbi kiszámítható időpontban ténylegesen nem kiszámítható. Így egy tetszetős fizikai mezőelmélet (jóllehet nem a mi világunkra ténylegesen igaz Maxwell-elmélet) egyenletei a Pour-El- és Richards-féle értelemben mutathatnak nem kiszámítható fejlődést!Míg azonban a Pour-El–Richards-féle eredmény bizonyára meglepő és matematikailag lényeges, fizikai értelemben valójában nem mond ellent a sejtésnek. A kiszámíthatósági sejtésnek.Pour-El és Richards ténylegesen bebizonyították, hogy a hullámegyenletben nem léphet fel nemkiszámíthatóság, ha az ilyen jellegű mezőt nem engedjük meg. Mindenesetre még ha meg is engedjük, nehezen látható, hogyan használhatná ki az ilyen nemkiszámíthatóságot bármilyen fizikai „eszköz” (mint az emberi agy?). Jelentősége csak akkor lehet, ha tetszőlegesen pontos méréseket engedünk meg, ami, mint korábban leírtam, fizikailag nem nagyon valószerű. Mindazonáltal a Pour-El–Richards-féle eredmények egy olyan fontos kutatás érdekes kezdeteit jelentik, amelyben eddig még keveset végeztek.
A Lorentz-féle mozgásegyenlet; elfutó részecskék
A Maxwell-egyenletek önmagukban nem alkotnak igazán teljes egyenletrendszert. Csodálatosan leírják az elektromos és mágneses mező terjedését, ha adott az elektromos töltések és áramok eloszlása. E töltések fizikailag töltött részecskék – ahogy ma tudjuk, főként elektronok és protonok –, az áramok pedig e részecskék mozgásából származnak. Ha tudjuk, hol vannak a részecskék és hogyan mozognak, akkor a Maxwell-egyenletek megmondják, hogyan viselkedik az elektromágneses mező. Nem mondják meg viszont, hogyan viselkednek maguk a részecskék. A kérdésre a választ részben már Maxwell idejében ismerték, de kielégítő egyenletrendszert 1895-ig nem írtak fel. Ekkor Hendrick Antoon Lorentz a speciális relativitáselmélettel rokon elképzeléseket használva levezette azt, amit ma egy töltött részecske Lorentz-féle mozgásegyenletének nevezünk (vö. Whittaker 1910, 310., 395. o.). Ezek az egyenletek megmondják, hogyan változik folytonosan egy töltött részecske sebessége az elektromos és mágneses mezőnek azon pontbeli értékétől függően, ahol a részecske éppen található.89 Ha a Maxwell-egyenletekhez hozzátesszük a Lorentz-egyenleteket, akkor megkapjuk mind a töltött részecskék, mind az elektromágneses mező időbeli fejlődésének szabályait.Nincs azonban minden rendben ezzel az egyenletrendszerrel. Kitűnő eredményeket ad akkor, ha a mezők nagyon egyenletesek egészen a részecskék átmérőinek méretéig lemenő skálákig (e méretnek az elektron „klasszikus sugarát” vesszük, ami kb. 10–15 m), és ha a részecskék mozgása nem túl heves. Van azonban itt egy elvi nehézség, amely más körülmények között fontos lehet. A Lorentz-egyenlet azt mondja nekünk, vizsgáljuk meg az elektromágneses mezőt pontosan abban a pontban, amelyben a töltött részecske van (hogy megtudjuk az „erőt” abban a pontban). Hol legyen ez a pont, ha a részecske mérete véges? Vegyük talán a részecske „középpontját”, vagy átlagoljuk a mezőt (hogy az erőt megkapjuk) a felület pontjaira? Ez különbséget eredményezhet, ha a mező a részecske skáláján nem egyenletes. Van egy másik, komolyabb probléma: milyen is valójában a mező a részecske felületén (vagy középpontjában)? Ne felejtsük el, hogy töltött részecskéről van szó. Maga is kelt elektromágneses mezőt, ezt hozzá kell adni a „háttérmezőhöz”, amelyben a részecske ül. „Felületéhez” nagyon közel a részecske saját mezője roppant erőssé válik, könnyen elnyom minden más mezőt. Továbbá a részecske mezője körös-körül többé-kevésbé közvetlenül kifelé (befelé) mutat, így a tényleges eredő mező, amelyre a részecskének válaszolnia kell, egyáltalán nem egyenletes, a részecske „felületén” különböző helyeken különböző irányokba mutat, nem is beszélve a „belsejéről” (5.15. ábra).
 Talán jobb, ha a részecskéket pontszerűeknek tekintjük. Ez azonban másféle problémákhoz vezet, mert saját elektromos mezője a részecske közvetlen szomszédságában végtelenné válik. Ha a részecskét a Lorentz-egyenletek szerint a saját helyén lévő elektromos mező irányítja, akkor egy végtelen mezőre kell válaszolnia! Hogy a Lorentz-erőtörvénynek értelme legyen, meg kell találnunk a módját annak, hogy levonjuk a részecske saját mezőjét, és így a véges háttérmező maradjon meg, amelyre a részecske egyértelműen tud válaszolni. A problémát, hogy ezt hogyan kell csinálni, 1938-ban Dirac oldotta meg (akiről később megint fogunk hallani). Dirac megoldása azonban riasztó következtetésekhez vezetett. Azt találta, hogy a részecskék és mezők viselkedését kezdeti adataik csak akkor határozzák meg, ha nem csak kezdeti helye és sebessége ismert minden részecskének, hanem a kezdeti gyorsulások is (ami a szokásos dinamikai elméleteket tekintve eléggé rendhagyó). E kezdeti gyorsulás legtöbb értéke mellett a részecske végül teljesen őrült módon viselkedik, önmagát gyorsítja olyan sebességre, amely nagyon gyorsan közelit a fény sebességéhez! Ezek Dirac „elfutó megoldásai”, amelyek nem felelnek meg semmi olyannak, ami a Természetben valóban megtörténik. A kezdeti gyorsulások helyes megválasztásával módot kell találni az elfutó megoldások kizárására. Ez mindig megtehető, de csak úgy, ha „jövőbelátást” építünk be – azaz a kezdeti gyorsulásokat olyan módon kell előírnunk, amely előre látja, mely megoldások válnak végül elfutókká, és elkerüli ezeket. Ez egyáltalán nem az a mód, ahogy egy szabványos, determinisztikus fizikai problémában a kezdeti adatokat előírjuk. A hagyományos determinizmusban ezek az adatok tetszőlegesen adhatók meg, minden megkötés nélkül a jövőbeli viselkedést illetően. Itt most nemcsak arról van szó, hogy a jövő tökéletesen meghatározott egy múltbeli időpontban előírható adatokkal, de magát az adatok előírását nagyon pontosan megszorítja az a követelmény, hogy a jövőbeli viselkedés valóban „ésszerű” legyen!Eddig jutunk el az alapvető klasszikus egyenletekkel. Az Olvasó látja, hogy a determinizmus és a kiszámíthatóság kérdése a klasszikus fizikai törvényekben zavarossá vált. Van-e valóban teleologikus elem a fizikai törvényekben, befolyásolja-e valahogy a jövő azt, hogy mi történhetett meg a múltban? A fizikusok a klasszikus elektrodinamika (a klasszikus töltött részecskék és az elektromos és mágneses mezők elmélete) ilyen velejáróit rendesen nem tekintik a valóság komoly leírásainak. Szokásos válaszuk a fenti nehézségekre az, hogy az egyedi töltött részecskék szigorúan véve tulajdonképpen a kvantumelektrodinamika birodalmába tartoznak, és nem várhatjuk, hogy szigorúan klasszikus eljárással értelmes válaszokat kapjunk. Ez kétségtelenül igaz, de amint később látni fogjuk, magának a kvantumelméletnek is vannak e téren problémái. Dirac valójában pontosan azért vizsgálta a töltött részecskék dinamikájának klasszikus problémáját, mert úgy gondolta, hogy az ötleteket adhat a (fizikailag megfelelőbb) kvantumos probléma még nagyobb, alapvető nehézségeinek megoldásához.
Talán jobb, ha a részecskéket pontszerűeknek tekintjük. Ez azonban másféle problémákhoz vezet, mert saját elektromos mezője a részecske közvetlen szomszédságában végtelenné válik. Ha a részecskét a Lorentz-egyenletek szerint a saját helyén lévő elektromos mező irányítja, akkor egy végtelen mezőre kell válaszolnia! Hogy a Lorentz-erőtörvénynek értelme legyen, meg kell találnunk a módját annak, hogy levonjuk a részecske saját mezőjét, és így a véges háttérmező maradjon meg, amelyre a részecske egyértelműen tud válaszolni. A problémát, hogy ezt hogyan kell csinálni, 1938-ban Dirac oldotta meg (akiről később megint fogunk hallani). Dirac megoldása azonban riasztó következtetésekhez vezetett. Azt találta, hogy a részecskék és mezők viselkedését kezdeti adataik csak akkor határozzák meg, ha nem csak kezdeti helye és sebessége ismert minden részecskének, hanem a kezdeti gyorsulások is (ami a szokásos dinamikai elméleteket tekintve eléggé rendhagyó). E kezdeti gyorsulás legtöbb értéke mellett a részecske végül teljesen őrült módon viselkedik, önmagát gyorsítja olyan sebességre, amely nagyon gyorsan közelit a fény sebességéhez! Ezek Dirac „elfutó megoldásai”, amelyek nem felelnek meg semmi olyannak, ami a Természetben valóban megtörténik. A kezdeti gyorsulások helyes megválasztásával módot kell találni az elfutó megoldások kizárására. Ez mindig megtehető, de csak úgy, ha „jövőbelátást” építünk be – azaz a kezdeti gyorsulásokat olyan módon kell előírnunk, amely előre látja, mely megoldások válnak végül elfutókká, és elkerüli ezeket. Ez egyáltalán nem az a mód, ahogy egy szabványos, determinisztikus fizikai problémában a kezdeti adatokat előírjuk. A hagyományos determinizmusban ezek az adatok tetszőlegesen adhatók meg, minden megkötés nélkül a jövőbeli viselkedést illetően. Itt most nemcsak arról van szó, hogy a jövő tökéletesen meghatározott egy múltbeli időpontban előírható adatokkal, de magát az adatok előírását nagyon pontosan megszorítja az a követelmény, hogy a jövőbeli viselkedés valóban „ésszerű” legyen!Eddig jutunk el az alapvető klasszikus egyenletekkel. Az Olvasó látja, hogy a determinizmus és a kiszámíthatóság kérdése a klasszikus fizikai törvényekben zavarossá vált. Van-e valóban teleologikus elem a fizikai törvényekben, befolyásolja-e valahogy a jövő azt, hogy mi történhetett meg a múltban? A fizikusok a klasszikus elektrodinamika (a klasszikus töltött részecskék és az elektromos és mágneses mezők elmélete) ilyen velejáróit rendesen nem tekintik a valóság komoly leírásainak. Szokásos válaszuk a fenti nehézségekre az, hogy az egyedi töltött részecskék szigorúan véve tulajdonképpen a kvantumelektrodinamika birodalmába tartoznak, és nem várhatjuk, hogy szigorúan klasszikus eljárással értelmes válaszokat kapjunk. Ez kétségtelenül igaz, de amint később látni fogjuk, magának a kvantumelméletnek is vannak e téren problémái. Dirac valójában pontosan azért vizsgálta a töltött részecskék dinamikájának klasszikus problémáját, mert úgy gondolta, hogy az ötleteket adhat a (fizikailag megfelelőbb) kvantumos probléma még nagyobb, alapvető nehézségeinek megoldásához.
Einstein és Poincaré speciális relativitáselmélete
Emlékezzünk vissza a Galilei-féle relativitási elvre, amely azt mondja, hogy Galilei és Newton fizikai törvényei teljesen változatlanok maradnak, ha álló vonatkoztatási rendszerből mozgóra térünk át. Ez azzal jár, hogy a szomszédságunkban lévő objektumok dinamikai viselkedésének egyszerű vizsgálatával nem tudjuk megállapítani, vajon állunk-e vagy egyenletes sebességgel mozgunk valamilyen irányban. (Emlékezzünk Galilei hajójára a tengeren.) Tegyük azonban fel, hogy e törvényekhez hozzátesszük Maxwell egyenleteit. Igaz marad-e ekkor is a Galilei-féle relativitás? Idézzük fel, hogy Maxwell elektromágneses hullámai állandó c sebességgel, a fény sebességével terjednek. A józan ész látszólag azt mondja, hogy ha nagyon gyorsan utazunk egy irányban, akkor azt kell látnunk, hogy a fény sebessége abban az irányban c alá csökken (mert úgy mozgunk, hogy abban az irányban utolérjük a fényt), az ellenkező irányban pedig megfelelően c fölé nő (mert eltávolodunk a fénytől) – tehát különbözik a Maxwell-elmélet rögzített értékétől. A józan észnek valóban igaza van: a kombinált Newton- és Maxwell-egyenletek nem elégítik ki a Galilei-féle relativitást.Az ilyen dolgokon való töprengés vezette el 1905-ben Einsteint – mint ahogy valójában előtte (1898 és 1905 között) Poincarét is – a speciális relativitáselmélethez. Poincaré és Einstein egymástól függetlenül azt találták, hogy a Maxwell-egyenletek is kielégítenek egy relativitási elvet (vö. Pais 1982); azaz az egyenletek hasonlóképpen változatlanok maradnak, ha álló vonatkoztatási rendszerről mozgóra térünk át, noha az áttérés szabályai eltérőek a Galilei–Newton-féle fizikára érvényesektől! Hogy a kettő összeférjen egymással, vagy az egyik, vagy a másik egyenletrendszert módosítani kell – vagy elhagyni a relativitási elvet.Einsteinnek nem állt szándékában elhagyni a relativitás elvét. Csodálatos fizikai ösztönével ragaszkodott ahhoz, hogy egy ilyen elvnek érvényesnek kell lennie világunk fizikai törvényeire. Jól tudta továbbá, hogy a Galilei–Newton-féle fizikát tulajdonképpen minden ismert jelenségben csak a fénysebességhez képest nagyon kicsi sebességekre ellenőrizték, ahol az eltérés nem jelentős. Csak magát a fényt ismerték mint olyat, ahol elég nagy sebességek fordulnak elő ahhoz, hogy az eltérések fontosak legyenek. Ezért a fény viselkedése világosíthatna fel bennünket arról, melyik relativitási elvet kell elfogadnunk – a fény viselkedését pedig a Maxwell-egyenletek kormányozzák. Ezért a Maxwell-elméletre érvényes relativitási elvet kell megtartani; a Galilei–Newton-féle törvényeket pedig eszerint kell módosítani!Lorentz, Poincaré és Einstein előtt, szintén felvetette és részben megválaszolta ezeket a kérdéseket. 1895-ben azt a nézetet fogadta el, hogy az anyagot összetartó erők elektromágneses természetűek (ahogy az valóban kiderült), ezért a valóságos anyagi testek viselkedése a Maxwell-egyenletekből származtatott törvényeknek kell eleget tegyen. Ennek egyik következménye az, hogy egy fénysebességhez közeli sebességgel mozgó test a mozgás irányában kismértékben összehúzódik („Fitzgerald–Lorentz-féle kontrakció”). Lorentz ezt egy rejtélyes kísérleti felfedezés magyarázatára használta. Az 1887-es Michelson–Morley-kísérlet volt ez, amely azt látszott mutatni, hogy az elektromágneses jelenségeket nem lehet egy „abszolút” nyugalmi rendszer meghatározására használni. (Michelson és Morley megmutatta, hogy a fény sebességét a Föld felszínén nem befolyásolja a Föld Nap körüli mozgása – nagyon komoly ellentétben a várakozásokkal.) Az anyag mindig úgy viselkedik-e, hogy (egyenletes) mozgását nem lehet lokálisan észlelni? Ez volt Lorentz hozzávetőleges következtetése; ő az anyag egy speciális elméletére korlátozódott, amelyben az elektromágneses erőkön kívül más erőket nem tekintettek lényegesnek. Poincaré, aki kitűnő matematikus volt, meg tudta mutatni (1905-ben), hogy van az anyag viselkedésének egy olyan egzakt, a Maxwell-egyenletek mögött húzódó relativitási elvnek eleget tevő módja, hogy az egyenletes mozgás lokálisan egyáltalán nem észlelhető. Nagyon sokat megértett az elv fizikai következményeiből is (többek között az „egyidejűség viszonylagosságát”, amire rövidesen sort kerítünk). Úgy tetszik, ő ezt csupán egy lehetőségnek tekintette, és nem osztotta Einstein meggyőződését, hogy valamilyen relativitási elvnek érvényesnek kell lennie.A Maxwell-egyenletek által kielégített relativitási elvet – amely speciális relativitás néven vált ismertté – egy kissé nehéz felfogni, és sok olyan nem intuitív vonása van, amelyeket első ránézésre nehéz a mi világunk valóságos tulajdonságainak elfogadni. A speciális relativitást nem lehet megfelelően értelmezni egy további alkotórész nélkül, amelyet 1908-ban vezetett be az igen eredeti és ötletdús orosz-német geométer, Herrmann Minkowski (1864–1909). Einstein egyik tanára volt a Zürichi Műegyetemen. Alapvető új elképzelése az volt, hogy a teret és időt, mint egyetlen dolgot, együtt kell vizsgálni: ez a négydimenziós téridő. 1908-ban a Göttingeni Egyetemen tartott híres előadásán Minkowski kijelentette: Ezentúl az önmagában vett tér és az önmagában vett idő az árnyékvilágban való eltűnésre van ítélve, és csak a kettő egyfajta egyesítése őrzi meg független realitását.Próbáljuk megérteni a speciális relativitás alapjait Minkowski nagyszerű téridőképén keresztül! A téridőfogalommal való megbarátkozás egyik nehézsége az, hogy négydimenziós, ami nehézzé teszi a megjelenítést. Ám miután túléltük találkozásunkat a fázistérrel, a csupán négy dimenzióval már semmi bajunk nem lesz! Mint előbb, most is „csalni” fogunk, és kevesebb dimenziójú teret ábrázolunk – a csalás mértéke azonban most összehasonlíthatatlanul kisebb, képünk ennek megfelelően pontosabb lesz. Két dimenzió (egy térbeli és egy időbeli) sokféle célra elegendő lenne, de remélem, az Olvasó megengedi nekem, hogy kissé merészebb legyek, és felmenjek háromig (két térbeli, egy időbeli). Ez nagyon jó képet fog nyújtani, és nem lesz nehéz elfogadni, hogy az elképzelések nem sok változtatással elvileg kiterjeszthetőek a teljes négydimenziós helyzetre. A téridődiagramról azt kell észben tartanunk, hogy minden pontja egy eseményt ábrázol – azaz egy pontot a térben egyetlen időpontban, egy pontnak ugyanis csak pillanatnyi létezése van. A teljes diagram az egész történetet, múltat, jelent, jövőt ábrázolja. Egy részecskét, mert az időben tovább él, nem pont, hanem vonal ábrázol, amelyet a részecske világvonalának nevezünk. A világvonal a részecske teljes történetét leírja: egyenes, ha a részecske egyenletesen mozog, görbült, ha gyorsul (azaz mozgása nem egyenletes).



Az 5.16. ábrán egy két tér- és egy idődimenziós téridőt rajzoltam le. Képzeljük el, hogy függőleges irányban mérve van egy szabványos t időkoordináta, vízszintesen mérve pedig két térkoordináta, x/c és z/c.90 A középen lévő kúp az O téridő kezdőpont (jövőbe mutató) fénykúpja. Hogy jelentőségét érzékeljük, képzeljünk el egy robbanást az O eseménynél. (A robbanás tehát a térbeli kezdőpontban, a t = 0 időpontban következik be.) A robbanásnál kibocsátott fény története ez a fénykúp. Kétdimenziós térben a fényvillanás története egy c fénysebességgel kifelé mozgó kör volna. A teljes háromdimenziós térben egy c sebességgel kifelé mozgó gömb – a fény gömb alakú hullámfrontja –, de itt most elhagyjuk az y térbeli irányt, így csak egy kört kapunk, hasonlót, mint a tóba dobott kő vízbeérési pontjából kiinduló kör alakú fodrok. A téridőképen is láthatjuk ezt a kört, ha gyorsan mozogva felfelé egymás után vízszintes metszeteket készítünk a kúpból. Ezek a vízszintes síkok különböző térbeli leírásokat ábrázolnak, ahogy a t időkoordináta nő. Na már most, a relativitáselmélet egyik sajátsága az, hogy egy anyagi részecske nem mozoghat gyorsabban a fénynél (erről többet később). A robbanásból jövő minden anyagi részecske le kell maradjon a fény mögött. A téridőképben ez azt jelenti, hogy a robbanásban kibocsátott összes részecske világvonalának a fénykúpon belül kell feküdnie.
A fényt gyakran kényelmes – fotonoknak nevezett – részecskék segítségével leírni. Pillanatnyilag gondolhatunk úgy egy „fotonra”, mint az elektromágneses mező nagyfrekvenciás oszcillációjának egy kis „csomagjára”. A fotonkép fizikailag megfelelőbb a kvantumos leírás összefüggéseiben, erről a következő fejezetben lesz szó, de most a „klasszikus” fotonok is segítségünkre lesznek. A fotonok szabad térben mindig egyenes vonalakon mozognak a c alapsebességgel. Ez azt jelenti, hogy a Minkowski-féle téridőképben egy foton világvonala mindig egy a függőlegessel 45°-os szöget bezáró, egyenes vonal. Az O-ban történt robbanásban keletkezett fotonok rajzolják meg az O középpontú fénykúpot.Ezek a tulajdonságok általánosan, a téridő minden pontjára érvényesek kell legyenek. A kezdőpontot nem tünteti ki semmi: az O pont nem különbözik semelyik másik ponttól. Ezért a téridő minden pontjában kell legyen egy fénykúp, amelynek ugyanaz a jelentése, mint a kezdőpontbeli fénykúpnak. Minden fényfelvillanás története – vagy ha jobban szeretjük a fény részecske leírását, akkor a fotonok világvonalai – mindig minden pontban a fénykúp mentén halad(nak), míg egy anyagi részecske története mindig minden pontban a fénykúpon belül kell legyen. Ezt mutatja az 5.17. ábra. A pontokhoz tartozó fénykúpok családja a téridő Minkowski-geometriája részének tekinthető.
Mi a Minkowski-geometria? Legfontosabb vonása a fénykúpszerkezet, de több annál. Van benne egy „távolság”-fogalom, amely figyelemre méltó hasonlóságokat mutat az euklideszi geometria távolságával. A háromdimenziós euklideszi geometriában egy pontnak a kezdőponttól mért r távolsága, a szokásos derékszögű koordinátákkal kifejezve, a következő:
r2 = x2 + y2 + z2. (Lásd 5.18a. ábra. Ez éppen a Pitagorasz-tétel – kétdimenziós alakja talán jobban megszokott.) Háromdimenziós Minkowski-geometriánkban a kifejezés formailag nagyon hasonló (5.18b. ábra), a lényeges különbség az, hogy most két mínuszjel van benne: s2 = t2 – (x/c)2 – (z/c)2. Helyesebben szólva, Minkowski-geometriánk természetesen négydimenziós, és a „távolság” kifejezése a következő: s2 = t2 – (x/c)2 – (y/c)2 – (z/c)2. Mi a fizikai jelentése az s „távolság”-mennyiségnek ebben a kifejezésben? Tegyük fel, hogy a kérdéses pont – azaz a {t, x/c, y/c, z/c} (vagy a háromdimenziós esetben a {t, x/c, z/c}) koordinátákkal adott P pont – O (jövőbe mutató) fénykúpján belül fekszik. Ekkor az OP egyenes szakasz egy anyagi részecske – mondjuk a robbanásban keletkező valamelyik részecske – történetének egy szakaszát ábrázolhatja. Az OP szakasz s Minkowski-„hosszának” közvetlen fizikai értelmezése van. Ez az az időtartam, amelyet a részecske valójában átélt az O és P események között! Azaz ha volna egy, a részecskéhez rögzített, nagyon tartós és pontos óra,91 akkor az O-ban és P-ben észlelt idők közötti különbség pontosan s volna. A várakozásokkal ellentétben maga a t koordináta mennyiség nem adja meg a pontos óra által mért időt, hacsak az nincs koordináta-rendszerünkben „nyugalomban” (azaz x/c, y/c, z/c koordinátái rögzítettek), ami azt jelenti, hogy az óra világvonala a diagramon „függőleges”. Így „t” csak a nyugalomban lévő (azaz „függőleges” világvonalú) megfigyelők számára jelent „időt”. Mozgó (az O kezdőponttól egyenletesen távolodó) megfigyelőnél az idő helyes mértékét a speciális relativitáselmélet szerint az s mennyiség adja.Ez nagyon figyelemreméltó – és teljesen eltér az idő „hétköznapi”, Galilei–Newton-féle mértékétől, ami egyszerűen a t koordinátaérték volna. Jegyezzük meg, hogy az s relativisztikus (Minkowski-féle) időmérték valamivel mindig kisebb, mint t, ha egyáltalán van mozgás (mert a fenti képlet szerint s2 kisebb, mint t2, amikor csak x/c, y/c és z/c nem mind nulla). A mozgás (azaz, ha OP nincs a t tengely mentén) „lelassítja” az órát t-hez képest, azaz koordinátarendszerünkből nézve. Ha a mozgás sebessége c-hez képest kicsi, akkor s és t majdnem azonos, ami megmagyarázza, miért nem vagyunk közvetlenül tudatában annak, hogy „a mozgó órák késnek”. A másik szélsőséges esetben, amikor a sebesség maga a fénysebesség, P a fénykúpon fekszik; és azt találjuk, hogy s = 0. A fénykúp pontosan azon pontok halmaza, amelyeknek O-tól mért „Minkowski-távolsága” (azaz „ideje”) éppen nulla. Így egy foton egyáltalán nem „tapasztalja” az idő múlását! (A még szélsőségesebb eset, amikor P a kúpon kívülre esik, nincs megengedve, mert ez képzetes s-hez vezetne – negatív szám négyzetgyöke képzetes – és sértené azt a szabályt, hogy anyagi részecskék vagy fotonok nem mozoghatnak gyorsabban, mint a fény.92)A Minkowski-féle „távolság”-fogalom egyformán jól alkalmazható a téridő „bármely” pontpárjára, amelyeknél az egyik a másik fénykúpjában fekszik – vagyis egy részecske elmehetne az egyikből a másikba. Helyezzük át O-t a téridő egy másik pontjába. A pontok közötti Minkowski-távolság ismét azt az időtartamot méri, amelyet az egyikből a másikba egyenletesen mozgó óra tapasztal. Ha megengedjük, hogy a részecske foton legyen, és így a Minkowski-távolság zérussá váljon, akkor két olyan pontot kapunk, amelyek közül az egyik rajta van a másik fénykúpján – ez a körülmény szolgál egy pont fénykúpjának definiálására.A Minkowski-geometria alapvető szerkezete a „hossz” e furcsa mértékével a világvonalakon – amit a fizikai órák által mért (vagy „tapasztalt”) időként értelmezünk – tartalmazza a speciális relativitáselmélet igazi lényegét. Megismerkedhet az Olvasó például a relativitás ún. ikerparadoxonával: egy ikerpár egyik tagja a Földön marad, a másik kirándulást tesz egy közeli csillagra, a fénysebességet megközelítő nagy sebességgel utazik oda és vissza. Visszaérkezésekor az ikrek úgy találják, hogy különbözőképpen öregedtek meg, az utazó még életerős ifjú, míg otthon maradt testvére öregember. A Minkowski-geometria segítségével ez könnyen leírható – és látható, hogy bár a jelenség rejtélyes, valójában miért nem paradoxon. Az AC világvonal az otthon maradó ikret ábrázolja, míg az utazó világvonala az AB és BC szakaszokból tevődik össze, ezek ábrázolják az utazás odafelé és visszafelé tartó részét (lásd 5.19. ábra). Az otthon maradó iker az AC Minkowski-távolsággal mért idő elmúlását tapasztalja, míg az utazó a két Minkowski-távolság, AB és BC összegével93 adott időét. Ezek az idők nem egyenlőek, azt találjuk, hogy AC > AB + BC, AC < AB + BC, ami azt állítja, hogy egy háromszög két oldalának összege mindig nagyobb, mint a harmadik. Ezt nem tekintjük paradoxonnak! Ahhoz teljesen hozzászoktunk, hogy egy út mentén két pont (most A és C) közötti távolság euklideszi mértéke a valóságosan megtett úttól függ. (Esetünkben az egyik AC, a hosszabb, megtört út ABC.) Ez a példa speciális esete annak a ténynek, hogy két pont (most A és C) között a legrövidebb távolságot az őket összekötő egyenes vonal (az AC vonal) mentén mérjük. Az egyenlőtlenség irányának megfordulása a Minkowski-esetben a „távolság” definíciójában fellépő előjelváltásból származik, ezért a Minkowski-féle AC „hosszabb”, mint az ABC egyesített út. E Minkowski-féle „háromszög-egyenlőtlenség” is egy általánosabb eredmény speciális példája: két eseményt összekötő világvonalak között a leghosszabb (a legnagyobb észlelt idő értelmében) az egyenes (azaz a gyorsulás nélküli). Ha két iker ugyanattól az A eseménytől indul és ugyanannál a C eseménynél fejezi be útját, közben az első közvetlenül, gyorsulás nélkül mozog A-tól C-ig, a másik viszont gyorsul, akkor az első mindig hosszabb idő elteltét tapasztalja, amikor újra találkoznak.ami mutatja, hogy az otthon maradó által tapasztalt idő nagyobb, mint az utazó által megélt.
Erőszakoltnak tűnhet, hogy intuitív fogalmainktól eltérően ilyen különös időmérést vezetünk be. Mára azonban már nagy mennyiségű kísérleti bizonyíték gyűlt össze ennek alátámasztására. Van például sok szubatomi részecske, amelyek bomlásainak (azaz más részecskékre való széteséseinek) ideje meghatározott. Ezek a részecskék olykor a fénysebességhez nagyon közeli sebességgel mozognak (például a kozmikus sugarakban, amelyek a világűrből érkeznek a Földre, vagy az ember készítette részecskegyorsítókban) és bomlásidejük pontosan úgy növekszik meg, ahogy azt a fenti meggondolásokból levezethetjük. Még meggyőzőbb az a tény, hogy ma már olyan pontos órák („nukleáris órák”) készíthetők, hogy ezek az időlassító hatások közvetlenül észlelhetők gyors, alacsonyan szálló repülőkön vitt órák segítségével – ezek a Minkowski-féle s „távolság”-mértéket erősítik meg és nem t-t! (Figyelembe véve a repülőgép magasságát, szigorúan számítva az általános relativitáselmélet kis, járulékos gravitációs hatásai is közbeszólnak, de ezek is egyeznek a megfigyeléssel; lásd a következő fejezetet.) Van még sok más, a speciális relativitás egész szerkezetével szoros kapcsolatban álló jelenség, amelyek folyamatosan részletes igazolást nyernek. Ezek egyikének, Einstein híres E = mc2 összefüggésének, amely hatásosan fejezi ki az energia és a tömeg egyenértékűségét, e fejezet vége felé tantaluszi kínokat okozó következményei lesznek számunkra!
Nem magyaráztam még el, hogyan illeszkedik be a relativitás elve a dolgoknak ebbe a rendjébe. Hogyan van az, hogy a különböző nagyságú, egyenletes sebességgel mozgó megfigyelők a Minkowski-geometriát illetően egyenértékűek lehetnek? Hogyan lehet az 5.16. ábra időtengelye („nyugvó megfigyelő”) teljesen egyenértékű egy másik egyenes világvonallal, mondjuk a meghosszabbított OP-vel („mozgó megfigyelő”)? Gondoljunk először az euklideszi geometriára. Bármely két egyenes vonal nyilvánvalóan teljesen egyenértékű egymással a geometria mint egész szempontjából. Elképzelhetjük, hogy az egész euklideszi teret „önmaga fölött mereven elcsúsztatjuk” addig, amíg az egyik egyenes a másik helyzetét veszi fel. Gondoljunk a kétdimenziós esetre, az euklideszi síkra. Képzeljük el, hogy egy darab papírt mozgatunk mereven egy síkfelületen úgy, hogy a papírra rajzolt tetszőleges egyenes vonal egybeesik a felület egy adott egyenes vonalával. Ez a merev mozgás megőrzi a geometria szerkezetét. Bár kevésbé nyilvánvalóan, de valami hasonló érvényes a Minkowski-geometriára, óvatosan kell viszont bánni a „merev” szóval. A csúsztatott papírdarab helyébe most egy sajátos anyagot kell gondolnunk – az egyszerűség kedvéért vegyük először a kétdimenziós esetet –, amelyben a 45°-os vonalak 45°-osak maradnak, az anyag ki tud nyúlni az egyik 45°-os irányban és megfelelően összehúzódni a másikban. Ezt mutatja az 5.20. ábra. Az 5.21. ábrán megpróbáltam érzékeltetni, mi történik a háromdimenziós esetben. A Minkowski-térnek ez a fajta „merev mozgása” – amelyet Poincaré-mozgásnak (vagy inhomogén Lorentz-mozgásnak) hívnak –, bár nem néz ki nagyon „merevnek”, de megőriz minden Minkowski-távolságot, és „megőrizni minden távolságot”, éppen ez az, amit a „merev” szó az euklideszi esetben jelent. A speciális relativitás elve azt állítja, hogy a fizika a téridő ilyen Poincaré-mozgásai során nem változik. Speciálisan az N „nyugvó” megfigyelő, akinek világvonala az 5.16. ábrán látható eredeti Minkowski-képünk időtengelye, tökéletesen egyenértékű fizikát lát az OP világvonalú M „mozgó” megfigyelő fizikájával.Minden t = állandó koordinátasík a „teret” ábrázolja egy „időpontban” az N megfigyelő számára, azaz események egy családját, amelyeket ő egyidejűnek (azaz mindegyiket „azonos időpontban” bekövetkezőnek) tekint. Nevezzük ezeket a síkokat N egyidejű tereinek. Amikor áttérünk egy másik M megfigyelőhöz, akkor egyidejű tereink eredeti családját egy új családba kell Poincaré-mozgással átvinnünk, hogy megkapjuk az M számára egyidejű tereket.94 Vegyük észre, hogy M egyidejű terei az 5.21. ábrán „felbillenteknek” látszanak. Ez a billenés rossz irányúnak tűnhet, ha az euklideszi geometria merev mozgásaiban gondolkodunk, de a Minkowski-esetben ezt kell várnunk. Amíg N azt gondolja, hogy tetszőleges t = állandó síkon minden esemény egy időben következik be, addig M másként látja a dolgokat: számára az ezekben a „felbillent” egyidejű terekben bekövetkező események látszanak egyidejűeknek! A Minkowski-geometriában önmagában nincs általános „egyidejűség” fogalom; minden egyenletesen mozgó megfigyelőnek saját elképzelése van arról, mit jelent az, hogy „egyidejű”.Tekintsük az 5.21. ábra két eseményét, R-et és Q-t. N szerint az R esemény megelőzi a Q-t, mert R korábbi egyidejű térben fekszik, mint Q; M szerint azonban más a helyzet, Q fekszik R-nél korábbi egyidejű térben. Így az egyik megfigyelő számára az R esemény megelőzi a Q-t, de a másik számára a Q előzi meg az R-et! (Ez csak azért történhet meg, mert R és Q térszerűen elválasztottak, ami azt jelenti, hogy mindkettő a másik fénykúpján kívül fekszik, anyagi részecske vagy foton nem utazhat át egyik eseménytől a másikig.) Nagy távolságra lévő eseményeknél, még egészen csekély relatív sebességek mellett is, jelentős különbségek lépnek fel az időrendezésben. Képzeljünk el két embert, amint lassan elsétálnak az utcán egymás mellett. Azok az Androméda-galaxisban (a Tejutunkhoz legközelebbi nagy galaxisban, kb. 20 000 000 000 000 000 000 km távolságban) lezajló események, amelyeket a két ember egymás melletti elhaladásukkal egyidejűnek ítél meg, több napnyi különbséget is mutathatnak (5.22. ábra). Az egyik ember szerint az űrhajó, amely azzal a szándékkal indul, hogy a Földön megsemmisítse az életet, már úton van; míg a másik szerint még a döntés sem született meg arról, hogy elindítsák-e az űrhajót vagy sem
Az 5.16. ábrán egy két tér- és egy idődimenziós téridőt rajzoltam le. Képzeljük el, hogy függőleges irányban mérve van egy szabványos t időkoordináta, vízszintesen mérve pedig két térkoordináta, x/c és z/c.90 A középen lévő kúp az O téridő kezdőpont (jövőbe mutató) fénykúpja. Hogy jelentőségét érzékeljük, képzeljünk el egy robbanást az O eseménynél. (A robbanás tehát a térbeli kezdőpontban, a t = 0 időpontban következik be.) A robbanásnál kibocsátott fény története ez a fénykúp. Kétdimenziós térben a fényvillanás története egy c fénysebességgel kifelé mozgó kör volna. A teljes háromdimenziós térben egy c sebességgel kifelé mozgó gömb – a fény gömb alakú hullámfrontja –, de itt most elhagyjuk az y térbeli irányt, így csak egy kört kapunk, hasonlót, mint a tóba dobott kő vízbeérési pontjából kiinduló kör alakú fodrok. A téridőképen is láthatjuk ezt a kört, ha gyorsan mozogva felfelé egymás után vízszintes metszeteket készítünk a kúpból. Ezek a vízszintes síkok különböző térbeli leírásokat ábrázolnak, ahogy a t időkoordináta nő. Na már most, a relativitáselmélet egyik sajátsága az, hogy egy anyagi részecske nem mozoghat gyorsabban a fénynél (erről többet később). A robbanásból jövő minden anyagi részecske le kell maradjon a fény mögött. A téridőképben ez azt jelenti, hogy a robbanásban kibocsátott összes részecske világvonalának a fénykúpon belül kell feküdnie.
Mi a Minkowski-geometria? Legfontosabb vonása a fénykúpszerkezet, de több annál. Van benne egy „távolság”-fogalom, amely figyelemre méltó hasonlóságokat mutat az euklideszi geometria távolságával. A háromdimenziós euklideszi geometriában egy pontnak a kezdőponttól mért r távolsága, a szokásos derékszögű koordinátákkal kifejezve, a következő:
Tekintsük az 5.21. ábra két eseményét, R-et és Q-t. N szerint az R esemény megelőzi a Q-t, mert R korábbi egyidejű térben fekszik, mint Q; M szerint azonban más a helyzet, Q fekszik R-nél korábbi egyidejű térben. Így az egyik megfigyelő számára az R esemény megelőzi a Q-t, de a másik számára a Q előzi meg az R-et! (Ez csak azért történhet meg, mert R és Q térszerűen elválasztottak, ami azt jelenti, hogy mindkettő a másik fénykúpján kívül fekszik, anyagi részecske vagy foton nem utazhat át egyik eseménytől a másikig.) Nagy távolságra lévő eseményeknél, még egészen csekély relatív sebességek mellett is, jelentős különbségek lépnek fel az időrendezésben. Képzeljünk el két embert, amint lassan elsétálnak az utcán egymás mellett. Azok az Androméda-galaxisban (a Tejutunkhoz legközelebbi nagy galaxisban, kb. 20 000 000 000 000 000 000 km távolságban) lezajló események, amelyeket a két ember egymás melletti elhaladásukkal egyidejűnek ítél meg, több napnyi különbséget is mutathatnak (5.22. ábra). Az egyik ember szerint az űrhajó, amely azzal a szándékkal indul, hogy a Földön megsemmisítse az életet, már úton van; míg a másik szerint még a döntés sem született meg arról, hogy elindítsák-e az űrhajót vagy sem
Einstein általános relativitás elmélete
Galilei meglátása: gravitációs mezőben minden test egyenlő gyorsan esik. (Galilei azt ismerte fel, hogy ha a levegő ellenállását nullára lehetne csökkenteni, akkor egyformán esnének.) Három évszázad telt el, míg e meglátás mély jelentőségét igazán felismerték és sarokkőként illlesztették be egy nagy elméletbe.Ez az elmélet Einstein általános relativitás elmélete-Az elmélet megalkotásához szükséges fogalom:
a görbült téridő , annak elképzelése....valóban igaz lehet-e, hogy Galilei régi meglátása tartalmazott valamit ami Newton elméletébe nincs beépítve? ...Mi szabja meg a gravitáció hatása alatt álló test gyorsulását?...Először van a testre ható erő, amelyről a gravitációs vonzás Newtom-törvénye azt mondja:...arányos a test tömegével. Másodszor: adott erő mellett a test gyorsulása fordítva arányos a test tömegével. Galilei meglátása azon a tényen alapul, hogy a Newton-féle gravitációs erőtörvényben szereplő "tömeg" ugyanaz, mint a Newton második törvé-nyében szerplő "tömeg".(Az azonosság helyett elegendő az arányosság.) Ez biztosítja, hogy a gravitáció hatására a test gyorsulása valóban független a tömegétől. Newton általános rendszerében semmi olyan nincs, ami megkövetelte volna, hogy ez a két tömegfogalom azonos legyen. Ezt Newton egyszerűen posztulálta. Az elektromos erők hasonlóak a gravitációsokhoz annyiban, hogy mindkettő inverz négyzetes erő, de előbbiek az elektromos töltéstől függnek, ami teljesen más, mint a Newton második törvényében szereplő tömeg."Galilei meglátása" az elekttromos erőkre nem alkalmazható: elektromos mezőben "elejtett" (töltött) tárgyak egyáltalán nem azonos sebességgel "esnek"!Most egyelőre egyszerűen fogadjuk el Galilei meglátását – a gravitációs mozgásra –, és keressük annak következményeit. Az űrrepülés ma az elképzelések jobb ellenőrzését kínálja, mert a világűrben valóban nincs levegő. Ott az „esés” a megfelelő gravitációs pályán való mozgást jelenti. Nem kell, hogy ez az „esés” lefelé, a Föld középpontja felé irányuljon. A mozgásnak vízszintes összetevője is lehet. Ha ez a vízszintes összetevő elég nagy, akkor lehet úgy „esni” a Föld körül, hogy a talajhoz semmivel nem jutunk közelebb! Gravitáció hatására szabad pályán mozogni, az „esés” egy finom (és nagyon drága!) módja. .... egy „űrsétát” végző űrhajós járművét úgy látja, hogy az előtte lebeg, az alatta lévő hatalmas Földgolyó gravitációs erejétől nem befolyásolva! (Lásd az 5.24. ábrát a könyvben) Így a gravitáció hatásait lokálisan ki lehet küszöbölni oly módon, hogy áttérünk a szabadesés „gyorsuló vonatkoztatási rendszerére”. ...A gravitáció a szabadeséssel ily módon kioltható, mert a gravitációs mező hatásai éppen olyanok, mint a gyorsulásé. Valóban, a felfelé gyorsuló lift belsejében a gravitációs mező növekedését érezzük, a lefelé gyorsulóban csökkenését. Ha a liftet tartó kötél elszakadna, akkor (a légellenállást és a súrlódást elhanyagolva) a létrejövő lefelé irányuló gyorsulás teljesen megszüntetné a gravitáció hatását, és a lift utasai – mint előbb az űrhajós – szabadon lebegnének, míg a lift be nem csapódna a földbe! A gyorsulás még egy vonatban vagy repülőgépen is lehet olyan, hogy a gravitáció nagyságát és irányát nem úgy érezzük, mint ahogy vizuális tapasztalatunk sugallná. Ez azért van így, mert a gyorsulás és a gravitáció hatásai hasonlóak, ezért érzékeink képtelenek azokat megkülönböztetni egymástól. Ezt a tényt – hogy a gravitáció lokális hatásai egyenértékűek egy gyorsuló vonatkoztatási rendszeréivel – Einstein az ekvivalencia elvének nevezte. ...A fenti megfontolások „lokálisak”. Ám ha elegendően pontos (és nem egészen lokális) méréseket tudunk végezni, akkor elvileg kideríthetünk egy különbséget az „igazi” gravitációs mező és az egyszerű gyorsulás között. Az 5.25. ábrán kissé eltúlozva azt mutatom be, hogyan kezdené befolyásolni a (newtoni) gravitációs mező nemegyenletessége a Föld gravitációs mezőjében szabadon eső részecskék kezdeti stacionárius, gömbszimmetrikus elrendezését. A mező két okból nem egyenletes. Először azért, mert a Föld középpontja véges távolságban van, a Föld felszínéhez közelebbi részecskék jobban gyorsulnak lefelé, mint azok, amelyek magasabban vannak (emlékezzünk Newton inverz négyzetes törvényére). Másodszor azért, mert ugyanezen okból a gyorsulás irányában is lesznek csekély különbségek a vízszintesen eltérő helyzetű részecskéknél. E nemegyenletesség következtében a gömbalak kissé torzulni kezd: egy „ellipszoidba”. A Föld középpontjának irányában (és az ellentétes irányban) megnyúlik, mert a középponthoz közelebbi részecskék valamivel nagyobb gyorsulást tapasztalnak, mint a távolabbiak; vízszintes irányban összehúzódik annak következtében, hogy a gyorsulás egy kissé befelé, a Föld középpontjának irányába mutat.
Ez a torzító hatás úgy ismert, mint a gravitáció árapályjelensége. Ha a Föld középpontját a Holddal, a részecskegömböt pedig a Föld felületével helyettesítjük, akkor pontosan előttünk áll a Hold árapályt előidéző hatása, mind a Hold irányában, mind az ellentétes irányban kidagadás jön létre. Az árapályjelenség a gravitációs mezőknek általános tulajdonsága, amelyet szabadeséssel nem lehet „kioltani”. Ez a jelenség a newtoni gravitációs mező nemegyenletességét méri. (Az árapálytorzítás nagysága a vonzócentrumtól mért távolság inverz köbe és nem inverz négyzete szerint csökken.)Newton inverz négyzetes erőtörvényét az árapályjelenség segítségével egyszerűen lehet értelmezni: annak az ellipszoidnak a térfogata, amellyé a gömb kezdetben95 torzul, egyenlő az eredeti gömb térfogatával – ha a gömb vákuumot vesz körül. Ez a térfogat-tulajdonság az inverz négyzetes törvényre jellemző; más erőtörvényre nem érvényes. Tegyük most fel, hogy a gömb nem vákuumot, hanem M össztömegű anyagot vesz körül. Az anyag gravitációs vonzásának következtében a gyorsulásnak most lesz egy további, befelé mutató összetevője. Az ellipszoid térfogata, amelybe részecskegömbünk kezdetben átmegy, összehúzódik – M-mel arányos mértékben. Egy példa a térfogatcsökkentő hatásra, ha gömbünkkel a Földet vesszük körbe állandó magasságban (5.26. ábra). Ekkor a Föld gravitációja által okozott, szokásos lefelé (azaz befelé) mutató gyorsulás okozza gömbünk térfogatának csökkenését. Ez a térfogatcsökkentő tulajdonság szabja meg Newton gravitációs erőtörvényének maradék részét, nevezetesen azt, hogy az erő arányos a vonzó test tömegével. Próbáljunk téridőképet készíteni a helyzetről! Az 5.27. ábrán (az 5.25. ábrán körrel ábrázolt) gömbfelületünk részecskéinek világvonalait tüntettem fel, a leírást abban a rendszerben végzem, amelyben a gömb középpontja nyugalomban van („szabadon esik”). Az általános relativitáselmélet a szabadesést „természetes mozgásnak” tekinti – a gravitációmentes fizika „egyenes vonalú, egyenletes mozgásának” mintájára. Ezért úgy próbálunk gondolni a szabadesésre, mint amelyet „egyenes” világvonal ír le a téridőben! Ám az 5.27. ábra tanúsága szerint zavaró az „egyenes” szó használata, és a terminológiát követve a szabadon eső részecskék világvonalait a téridő geodetikusainak fogjuk nevezni.Jó-e ez a terminológia? Mit értünk rendesen „geodetikuson”? Vizsgáljunk meg egy hasonló helyzetet egy kétdimenziós görbült felületen. A geodetikusok azok a görbék a felületen, amelyek (lokálisan) a „legrövidebb utak”. Ha gondolatban egy rugót húzunk ki a felületen (nem túl hosszút, mert akkor elcsúszhat), akkor az a felület egy geodetikusa mentén fog elhelyezkedni. Az 5.28. ábrán két példát mutatok a felületekre, az elsőt „pozitív görbületűnek” nevezik (a gömb felületéhez hasonló), a második „negatív görbületű” (nyeregszerű felület). A pozitív görbületű felületen két szomszédos geodetikus, amelyek egymással párhuzamosan indulnak, egymás felé kezdenek hajlani; a negatív görbületűn egymástól széthajlanak. Ha elképzeljük, hogy a szabadon eső részecskék világvonalai valamilyen értelemben olyanok, mint egy felület geodetikusai, akkor látjuk, hogy közeli a hasonlóság az előbb tárgyalt gravitációs árapályjelenség és egy felület görbületi hatásai között – most azonban a pozitív és negatív görbületi hatások egyaránt jelen vannak. Nézzünk az 5.25. és 5.27. ábrákra. Látjuk, hogy téridő-„geodetikusaink” az egyik irányban kezdenek szétválni egymástól (amikor a Föld irányába haladnak) – mint a negatív görbületű felületen az 5.28. ábrán –, a másik irányban egymás felé kezdenek hajlani – mint az 5.28. ábra pozitív görbületű felületén. Valóban úgy látszik, hogy téridőnknek „görbülete” van, hasonlóan kétféle felületünkhöz, de a magasabb dimenzió miatt azoknál bonyolultabb, és különböző elmozdulásoknál pozitív és negatív görbületek összekeveredve jelentkeznek. Ez mutatja, hogyan használható a „görbület” fogalma a téridőben a gravitációs mezők hatásának leírására. Az ilyen leírás használatának lehetősége végül is Galilei meglátásából (az ekvivalencia elvéből) következik, és megengedi, hogy a szabadeséssel kiküszöböljük a gravitációs „erőt”. Amit eddig mondtam, az nem követeli meg, hogy túlmenjünk Newton elméletén. Az új kép csak átfogalmazása az elméletnek.96 Új fizika keletkezik azonban, amikor ezt a képet megpróbáljuk összekombinálni azzal, amit megtanultunk a speciális relativitás Minkowski-féle leírásából – a téridő geometriájából, amelyről már tudjuk, hogy gravitáció hiányában alkalmazható. A kombináció eredménye Einstein általános relativitáselmélete. Minkowski geometriáját egzaktnak vesszük, ha nincs gravitációs mező – azaz nincs téridőgörbület. Amikor azonban gravitáció van jelen, akkor a Minkowski-geometriát csak közelítőnek tekintjük – ugyanúgy, ahogy egy sima felület csak közelítő leírását adja egy görbült felület geometriájának. Ha elképzeljük, hogy egyre erősebb mikroszkóppal vizsgálunk egy görbült felületet – ekkor a felület geometriája egyre nagyobb mértékben látszik megnyújtottnak –, akkor a felület egyre simábbnak látszik. Azt mondjuk, hogy egy görbült felület lokálisan olyan, mint egy euklideszi sík.97 Ugyanígy azt mondhatjuk, hogy gravitáció jelenlétében a téridő lokálisan Minkowski-geometriához hasonló (ami sima téridő), de nagyobb skálán megengedünk bizonyos „görbültséget” (lásd az 5.29. ábrát). A téridő minden pontja egy fénykúp csúcsa, éppen úgy, mint a Minkowski-térben, de ezek a fénykúpok nem teljesen egyformán állnak, nem olyan egyenletesen, mint a Minkowski-térben. A 7. fejezetben látni fogjuk a téridőmodellek néhány példáját, amelyekben ez a nemegyenletesség szemmel látható (vö. a 7.13., 7.14. ábrákat). Az anyagi részecskék világvonalai olyan görbék, amelyek mindig a fénykúpok belsejében haladnak, a fotonok görbéi a fénykúpok mentén. Bármelyik görbe mentén van „Minkowski-távolság”, amely a részecskék által átélt időt méri éppúgy, mint a Minkowski-térben. E távolságmérték a görbült felületekhez hasonlóan egy geometriát definiál a felületen, amely különbözhet a sík geometriájától.A téridő-geodetikusoknak most hasonló értelmezés adható, mint a kétdimenziós felületek előbb vizsgált geodetikusainak, de nem szabad elfelejtkeznünk a Minkowski- és euklideszi helyzetek különbségeiről. Így geodetikus világvonalaink a téridőben nem (lokálisan) minimális hosszúságú görbék, hanem olyanok, amelyek (lokálisan) maximálják a „távolságot” (azaz időt) a világvonal mentén. A gravitáció hatására szabad mozgást végző részecskék világvonalai e szabály szerint valóban geodetikusok. Így speciálisan e geodetikusok jól leírják a gravitációs mezőben mozgó égitesteket. Továbbmenve: az üres térben a fénysugarak (a fotonok világvonalai) szintén geodetikusok, de ezek zérus „hosszúságúak”.98 Példaként az 5.30. ábrán vázlatosan felrajzoltam a Föld és a Nap világvonalait: a Föld Nap körüli mozgása egy „dugóhúzó”-szerű geodetikus a Nap világvonala körül. Bejelöltem egy fotont is, amely egy távoli csillagból jut a Földre. Ennek világvonala kissé „íveltnek” látszik annak következtében, hogy a fényt Einstein elmélete szerint a Nap gravitációs mezője elhajlítja.
A négydimenziós téridő görbületének teljes matematikai kifejezését (amelynek egy adott pontban minden lehetséges irányban mozgó részecskékre le kell írnia az árapályjelenséget) az ún. Riemann-féle görbületi tenzor adja meg. Ez eléggé bonyolult valami, megadásához minden pontban húsz valós szám szükséges. Ezt a húsz számot a tenzor komponenseinek nevezzük. A különböző komponensek a téridő különböző irányainak különböző görbületeire vonatkoznak. A Riemann-féle görbületi tenzorra rendszerint az Rijkl jelölést használják, de az egyszerűség kedvéért azt fogom írni, hogy RIEMANN. E tenzort egy bizonyos módon két részre lehet bontani, Weyl-tenzornak nevezik az egyik részt, Ricci-tenzornak a másikat (mindkettőnek tíz komponense van). E szétbontást jelképesen így fogom írni: RIEMANN = WEYL + RICCI. (A részletes kifejezések különösebben nem segítenének bennünket.) A WEYL Weyl-tenzor szabadon eső részecskegömbünk árapálytorzítását méri (a kezdeti alakváltozást és nem a méretváltozást), a RICCI Ricci-tenzor pedig a kezdeti térfogatváltozást.99 Emlékezzünk vissza, hogy a newtoni gravitációs elmélet szerint az eső gömb által körülvett tömeg arányos e kezdeti térfogatcsökkenéssel. Ez durván szólva azt mondja nekünk, hogy az anyag tömegsűrűségét – vagy ami ezzel egyenértékű, energiasűrűségét (mert E = mc2) – a Ricci-tenzorral kell egyenlővé tenni.Alapvetően ennyit állítanak az általános relativitáselmélet mezőegyenletei – nevezetesen az Einstein-féle mezőegyenletek.100 Vannak azonban ezzel kapcsolatban bizonyos technikai dolgok, amelyeket most jobb nem firtatni. Elég lesz annyi, hogy van egy energia-impulzus tenzornak nevezett mennyiség, amely összefogja az anyag és az elektromágneses mezők energiájára, nyomására és impulzusára vonatkozó összes lényeges információt. Ezt a tenzort úgy fogom jelölni, hogy ENERGIA. Az Einstein-egyenletek nagyon formálisan a RICCI = ENERGIA alakban írhatók. (A „nyomás” jelenléte az ENERGIA tenzorban, valamint az egész egyenletrendszerre vonatkozó konzisztenciakövetelmények – ezek együttes következménye, hogy a nyomás szintén hozzájárul az előbb leírt térfogatcsökkentő hatáshoz.)Az egyenlet, úgy látszik, semmit nem mond a Weyl-tenzorról. Ez azonban fontos mennyiség. Az üres térben tapasztalt árapályjelenség teljesen a WEYL következménye. A fenti Einstein-egyenletek valójában maguk után vonják, hogy vannak differenciálegyenletek, amelyek a WEYL-t kötik össze az ENERGIÁ-val, eléggé hasonlóak, mint a korábban megismert Maxwell-egyenletek.101 Valóban gyümölcsöző nézőpont úgy tekinteni WEYL-t, mint az (E, B) párral leírt elektromágneses mezőmennyiségek egyfajta gravitációs analogonját (ténylegesen ezek is tenzort alkotnak – a Maxwell-tenzort). Így bizonyos értelemben WEYL a gravitációs mezőt méri. A WEYL „forrása” az ENERGIA tenzor, ami analóg azzal, hogy az (E, B) elektromágneses mező forrása (ρ, j), tehát a Maxwell-elmélet töltései és áramai. Ez a nézőpont segítségünkre lesz a 7. fejezetben.Ha a megfogalmazás és az alapul szolgáló ideák ilyen meglepő különbségeire gondolunk, akkor figyelemre méltó lehet, hogy nehéz megfigyelhető különbségeket találni az Einstein-elmélet és ama másik között, amelyet Newton állított fel két és fél évszázaddal korábban. Feltéve azonban, hogy a szóban forgó sebességek a fény c sebességéhez képest kicsik, és hogy a gravitációs mezők nem túl erősek (a szökési sebességek sokkal kisebbek, mint c; vö. 7. fejezet), az Einstein-elmélet a Newtonéval tulajdonképpen azonos eredményeket ad. Ám azokban az esetekben, amelyekben a két elmélet jóslatai különböznek, az Einstein-elmélet a pontosabb. Ma már van néhány ilyen, nagyon meggyőző kísérleti ellenőrzés, amelyek teljesen igazolják Einstein modernebb elméletét. Az órák gravitációs mezőben, ahogy Einstein állította, nagyon picit késnek. Ezt a jelenséget mára már sok különböző módon közvetlenül megmérték. A Nap valóban eltéríti a fényt és a rádiójeleket, és e találkozás kissé lelassítja azokat – ezek is jól ellenőrzött hatásai az általános relativitásnak. Az űrszondák és bolygók mozgásában a newtoni pályákhoz kis korrekciók járulnak, amint azt Einstein elmélete megköveteli; kísérletileg ezt is igazolták. (A Merkur bolygó mozgásában fellelhető, „perihéliumelfordulás” néven ismert anomáliát, amely a csillagászokat 1859 óta foglalkoztatja, Einstein 1915-ben megmagyarázta.) Mind közül talán a legmeggyőzőbb a két kicsi, nagy tömegű csillagból (feltehetően „neutroncsillagokból”, vö. 7. fejezet) álló, kettős pulzárnak nevezett rendszeren végzett megfigyeléssorozat, amely nagyon jól egyezik Einstein elméletével, és közvetett módon igazol egy olyan jelenséget, a gravitációs hullámok kibocsátását, amely Newton elméletéből teljesen hiányzik. (A gravitációs hullám az elektromágneses hullám gravitációs analogonja, amely a fény c sebességével terjed.) Nincs olyan megerősített megfigyelés, amely ellentmond Einstein általános relativitáselméletének. Minden kezdeti furcsasága ellenére Einstein elmélete határozottan a mi kincsünk!
Relativisztikus
kauzalitás és determinizmus
Emlékezzünk arra, hogy a
relativitáselméletben az anyagi testek nem mozoghatnak a fénynél gyorsabban –
abban az értelemben, hogy világvonalaiknak mindig a fénykúpokon belül kell
haladniuk (vö. 5.29. ábra).
(Az általános relativitáselméletben a dolgokat ilyen lokális módon kell
megfogalmaznunk. A fénykúpok nem rendeződnek el egyenletesen, így nem volna sok
értelme azt mondani, hogy egy nagyon távoli részecske
sebessége felülmúlja-e az itteni fénysebességet.) A fotonok
világvonalai a fénykúpok mentén fekszenek, de semmilyen
részecske világvonala nem haladhat a kúpokon kívül. Valójában
egy általánosabb állításnak kell igaznak lennie, nevezetesen annak, hogy
semmilyen jel nem mehet a fénykúpon kívül.
Hogy megértsük, miért
kell ennek így lennie, nézzük meg a Minkowski-térről rajzolt képeket (5.31. ábra). Tegyük
fel, hogy készítettünk egy eszközt, amely a fényénél kicsit nagyobb sebességű
jelet képes küldeni. A W megfigyelő jelet küld ezzel az
eszközzel a világvonalán lévő A eseményből egy távoli B eseményhez,
amely valamivel A fénykúpja alatt fekszik. Az 5.31a. ábrán
ezt W nézőpontjából rajzoltuk le, de az 5.31b. ábrán
az egészet újrarajzoltuk egy második, U megfigyelő
nézőpontjából, aki gyorsan távolodik W-től (mondjuk egy A és B közötti
ponttól), és akinek számára a B esemény korábbinak látszik,
mint az A! (Ez az „átrajzolás” egy Poincaré-mozgás, amint azt
korábban már leírtuk.) U egyidejű terei W nézőpontjából
„megbillenteknek” látszanak, ezért láthatja U korábbinak
a B eseményt, mint az A-t. Így a W által
kibocsátott jelet U az időben visszafelé mozgónak látná!
Ez még nem teljesen
ellentmondás. Ám nézzük most a dolgokat U nézőpontjából, szimmetrikusan (a speciális relativitás
elve szerint). Egy harmadik, V megfigyelő U-tól W-vel ellentétes irányban távolodva, ugyanolyan eszközzel
felszerelve, mint W, szintén ki tudna bocsátani egy a fénynél valamivel gyorsabb
jelet az ő (azaz V) nézőpontjából hátrafelé, U irányába. U ezt a jelet is az időben hátrafelé mozgónak látná, most
az ellentétes térbeli irányban. V leadhatna ezt a második jelet W felé hátra abban a pillanatban (B), amikor ő megkapja a W által küldött eredeti jelet. A második jel W-t egy C eseménynél éri el, amely U megítélése szerint korábbi, mint az eredeti kibocsátás A eseménye (5.32. ábra). Ám ennél még rosszabb, hogy a C esemény W saját világvonalán korábbi, mint az A, így W a C esemény bekövetkeztét valójában előbb tapasztalja, mint ahogy A-nál a jelet ő kibocsátja! Az üzenet, amelyet a V megfigyelő visszaküld W-hez, előzetes megegyezés alapján egyszerűen
megismételhetné a B-ben kapott üzenetet. Így W világvonalán korábbi időpontban kapja meg ugyanazt az
üzenetet, mint amelyet ő küld később! A két megfigyelőt elegendően nagy
távolságra szétválasztva elérhető, hogy a visszatérő jel olyan nagy
időkülönbséggel előzze meg az eredeti jelet, amilyennel csak akarjuk. W eredeti üzenete talán az, hogy eltörte a
lábát. A visszaküldött üzenetet még azelőtt megkaphatná, mielőtt a baleset bekövetkezne, és így
(feltehetően) szabad akaratából elkerülhetné azt!
Így a „fénynél
gyorsabb” jeladás és Einstein relativitási elve együtt ordító ellentmondáshoz
vezet normális „szabad akarat” érzésünkkel. A dolog ennél valójában még
komolyabb. Elképzelhetnénk, hogy talán a „W megfigyelő” csupán egy
úgy programozott mechanikus eszköz, hogy „IGEN” üzenetet küldjön, ha „NEM”-et
kap és fordítva. V is lehet mechanikus eszköz, de úgy
programozva, hogy ha „NEM”-et kap, küldje vissza a „NEM”-et, ha „IGEN”-t kap,
küldje vissza az „IGEN”-t. Ez ugyanahhoz a lényeges ellentmondáshoz vezet,
amelyet az előbb láttunk,102 most
látszólag függetlenül attól a kérdéstől, van-e vagy nincs a W megfigyelőnek
„szabad akarata”, és azt mondja nekünk, hogy egy fénynél gyorsabb jelet
kibocsátó eszköz „nem működhet” mint fizikai lehetőség. Ennek a későbbiekben
még lesznek rejtélyes következményei (6. fejezet).
Fogadjuk tehát el,
hogy semmiféle jel – nem csupán a közönséges fizikai
részecskék által hordozottak – nem kerülhet a fénykúpokon kívülre. Az előző
érvelés a speciális relativitást használja, de a speciális
elmélet szabályai lokálisan érvényesek maradnak az általános
relativitáselméletben. A speciális relativitás lokális érvényessége mondja azt,
hogy a fénykúpok magukba zárnak minden jelet, ezért ez igaz kell legyen az
általános elméletben is. Látni fogjuk, hogyan befolyásolja ez a determinizmus kérdését
ezekben az elméletekben. Emlékezzünk vissza, hogy a newtoni (vagy hamiltoni
stb.) rendszerben a „determinizmus” azt jelenti, hogy „egy speciális
időpontbeli kezdeti adatok” teljesen meghatározzák a viselkedést minden más
időpontban. Ha a newtoni elméletben téridő-leírásmódot alkalmazunk, a
„speciális időpont”, amelyben az adatokat előírjuk, a négydimenziós téridő
valamely háromdimenziós „metszete” volna (azaz az egész tér abban az egy
időpontban). A relativitáselméletben nincs globális „idő”, ami erre a célra
kiválasztható volna. A szokásos eljárás az, hogy rugalmasabb hozzáállást
fogadunk el. Bárki „ideje” megteszi. A speciális relativitáselméletben a
kezdeti adatok előírására az előbbi „metszetnek” bármelyik megfigyelő egyidejű
terét vehetjük. Az általános relativitáselméletben azonban az „egyidejű tér”
fogalom nem jól meghatározott. Helyette a térszerű felület általánosabb
fogalmát használhatjuk.103
A speciális relativitáselméletben a
determinizmus úgy fogalmazható meg, hogy a tetszőlegesen adott S egyidejű téren rögzített kezdeti adatok
meghatározzák a viselkedést az egész téridőben. (Ez a Maxwell-elméletre is
igaz, amely valójában „speciális-relativisztikus” elmélet.) Lehet azonban
erősebb állítást is tenni. Ha tudni akarjuk, mi fog történni az S jövőjében fekvő valamely P eseménynél, ahhoz a kezdeti adatokat nem
kell az egész S-ben tudnunk, csak egy korlátos (véges) tartományában. Ennek
oka az, hogy az „információ” nem terjedhet gyorsabban, mint a fény, így S-nek azok a pontjai, amelyek túl messze fekszenek
ahhoz, hogy belőlük fényjel érje el P-t, nem lehetnek hatással P-re (lásd az 5.34. ábrát).104 Ez sokkal kielégítőbb, mint a newtoni
esetben létrejövő helyzet, ahol elvileg tudnunk kellene, mi történt a teljes végtelen „metszeten”, hogy egyáltalán jóslatot
tehessünk, mi fog történni tetszőleges pontban egy pillanattal később. Nincs
megszorítás arra, milyen sebességgel terjedhet a newtoni információ, a newtoni
erők valójában pillanatszerűek.
A
„determinizmus” az általános relativitáselméletben jóval bonyolultabb dolog, mint a speciálisban, és csak
néhány megjegyzést fogok ezzel kapcsolatban tenni. Elsősorban egy S térszerű felületet (és nem egyidejű felületet) kell használnunk
a kezdeti adatok előírására. Ekkor az a helyzet, hogy az Einstein-egyenletek a
gravitációs mező lokálisan determinisztikus viselkedését adják, feltéve (mint
szokásosan), hogy az ENERGIA tenzorhoz járulékot adó anyagmezők determinisztikusan
viselkednek. Vannak azonban jelentős bonyodalmak. Maga a téridő geometriája –
fénykúp „kauzalitás”-szerkezetével együtt – most része annak, ami ténylegesen
meghatározásra kerül. E fénykúpszerkezetet időben előre nem ismerjük, így nem
tudjuk megmondani, S mely részeire van szükség, hogy meghatározzuk a
viselkedést egy jövőbeli P eseménynél. Bizonyos szélsőséges esetekben
előfordulhat, hogy az egész S sem elegendő, következésképpen a globális determinizmus
elvész! (Nehéz kérdések kerülnek itt elő, és az általános relativitáselmélet
egy fontos megoldatlan problémájához, az ún. „kozmikus cenzúrához” kapcsolódnak
– aminek köze van a fekete lyukak létrejöttéhez (Tipler és mások 1980; vö. 7. fejezet) Nagyon valószínűtlennek látszik, hogy a „szélsőséges”
gravitációs mezőknél esetleg bekövetkező, bármiféle „determinizmuskudarcnak”
közvetlen hatása volna az emberi skálájú dolgokra,...de azért ez a hiány, nem teljesség, nem teljes érvényesség nyugtalanítja Penroset.
Kiszámíthatóság a
klasszikus fizikában: hogyan is állunk?
E fejezetben végig próbáltam szemmel tartani
a kiszámíthatóság kérdését, mint ami különbözik a
determinizmusétól, és próbáltam jelezni, hogy amikor a „szabad akarat” és a
szellemi jelenségek kérdéseit tárgyaljuk, akkor a kiszámíthatósági problémák
legalább annyira fontosak, mint a determinizmus. Kiderült azonban, hogy a
determinizmus önmagában sem egészen olyan világos a klasszikus elméletben, mint
ahogy azt elhitették velünk. Láttuk, hogy a töltött részecske mozgásának
klasszikus Lorentz-egyenlete zavaró problémákat vet fel. (Emlékezzünk Dirac „elfutó
megoldásaira”.) Észrevettük azt is, hogy a determinizmussal az általános
relativitáselméletben is vannak nehézségek. Amikor az ilyen elméletekben nincs
determinizmus, akkor bizonyára nincs kiszámíthatóság sem. Mégis, egyik
felidézett esetben sem látszik úgy, hogy a determinizmus hiányának számottevő
közvetlen filozófiai jelentősége volna számunkra. Szabad akaratunk számára még
nincs „hely” ezekben a jelenségekben: az első esetben azért, mert úgy
gondoljuk, hogy pontszerű részecskére a klasszikus Lorentz-egyenlet (ahogy
Dirac megoldotta) fizikailag nem megfelelő azon a szinten, ahol ezek a
problémák fellépnek; a másodikban azért, mert azok a skálák, ahol a klasszikus
általános relativitáselmélet ilyen problémákhoz vezethet (fekete lyukak stb.),
teljesen eltérőek agyunk skáláitól.
Hogy állunk akkor most
a kiszámíthatósággal a klasszikus elméletben? Ésszerű az a
sejtés, hogy az általános relativitáselmélet helyzete nem különbözik jelentősen
a speciálisétól – túl a kauzalitásban és a determinizmusban lévő különbségeken,
amelyekről éppen az előbb beszéltem. Ahol a fizikai rendszer jövőbeli
viselkedését a kezdeti adatok meghatározzák, ott ez a jövőbeli viselkedés (hasonló
okokból, mint amelyeket a newtoni elméletnél kifejtettem) az adatok által kiszámíthatóan meghatározottnak
látszik105 (eltekintve
a nemkiszámíthatóságnak attól a „nem éppen segítőkész” típusától, amelyet
Pour-El és Richards a hullámegyenletnél találtak – és amely folytonosan változó
adatok mellett nem lép fel). Valójában nehéz látni, hogy bármelyik eddig
megvizsgált fizikai elméletben lehetnének jelentős „nem kiszámítható” elemek.
Azt biztosan várnunk kell, hogy az elméletek közül sokban bekövetkezhet az a
„kaotikus” viselkedés, amikor nagyon kis változások a kezdeti adatokban
hatalmas különbségeket okozhatnak az eredő viselkedésben. (Ez a helyzet látszik
az általános relativitásban, vö. Misner 1969, Belinskii és
mások 1970.) De amint az előbb említettem, nehéz azt látni, hogy a
nemkiszámíthatóságnak ez a fajtája – azaz a „jósolhatatlanság”
– bármilyen „hasznára” lehet egy eszköznek, amely megpróbálja „kiaknázni” a
fizikai törvényekben lévő lehetséges nem kiszámítható elemeket. Ha az „értelem”
bármiképp hasznosíthatja ezeket, akkor úgy látszik, a klasszikus fizikán kívül
kell lenniük ezeknek az elemeknek. E kérdést később újra meg kell vizsgálnunk,
miután már vetettünk egy pillantást a kvantumelméletre.
.........
1./
Szabad akaratunk számára még nincs
„hely” ezekben a jelenségekben: az első esetben azért, mert úgy gondoljuk, hogy
pontszerű részecskére a klasszikus Lorentz-egyenlet (ahogy Dirac megoldotta)
fizikailag nem megfelelő azon a szinten, ahol ezek a problémák fellépnek; a
másodikban azért, mert azok a skálák, ahol a klasszikus általános
relativitáselmélet ilyen problémákhoz vezethet (fekete lyukak stb.), teljesen
eltérőek agyunk skáláitól. - írja.
…teljesen eltérőek agyunk skáláitól…és előtte zárójelben, hogy például hol uralkodnak azok az eltérő
skálák (fekete lyukak
stb.)
Többször felvillantja azt, amit a magamfajta halandó szeretne
elkapni, hiú remény, hogy megérteni, csak elkapni, vagy legalábbis megérinteni.
Egy régen olvasott- elég jó –
fantasztikus regényben egy űrhajót magába ránt egy fekete lyuk. Öten vagy hatan
utaztak a hajón. A könyv utolsó oldalának történései már a „szingularitáson”
túlról szólnak: az események helyszíne ott a lyuk túloldalán nem a túlvilág, és
nem is az a klinikai halálból visszatértek emlékidézéseiben derengő gyöngyház-szín
szórású, sejtelmes, békés, hívogató fény (nagyon szeretem Kandinszkij: A fény,
amely nem okoz fájdalmat című festményét); nem, ez a valami ahová az került ami
valaha a hajó és utasai voltak, ez egy az elemei közötti kapcsolatot,
párbeszédet, egymás érzékelését lehetővé tevő környezet…és az űrhajósok, vagyis
azok a még szubatomi részecskékhez sem hasonlítható valamik, amik belőlük
maradtak, csodálva érzékelik a helyet, a helyzetet, ezt a gyöngyházfény –világot,
és rögtön közlik is „egymással”, amit „átélnek”, „éreznek”, „érzékelnek”, „észlelnek”
és „látnak”.
2./
De amint az előbb említettem, nehéz azt
látni, hogy a nemkiszámíthatóságnak ez a fajtája – azaz a
„jósolhatatlanság” – bármilyen „hasznára” lehet egy eszköznek, amely
megpróbálja „kiaknázni” a fizikai törvényekben lévő lehetséges nem kiszámítható
elemeket. Ha az „értelem” bármiképp hasznosíthatja ezeket, akkor úgy látszik, a
klasszikus fizikán kívül kell lenniük ezeknek az elemeknek. E kérdést később
újra meg kell vizsgálnunk, miután már vetettünk egy pillantást a
kvantumelméletre.
…
… Ha az „értelem” bármiképp hasznosíthatja ezeket,
akkor úgy látszik, a klasszikus fizikán kívül kell lenniük ezeknek az elemeknek…
…
„értelem”
…
’a valami bennünk ül és figyel’
– kapisgáltam ezt valamikor negyedikes gimnazista koromban egy írásomban.
„Én túllépek e mai kocsmán,
az értelemig és tovább!” [József Attila]
Tömeg, anyag és
valóság
Tekintsük röviden át a világnak azt a
képét, amelyet a klasszikus fizika nyújt számunkra. Először is van egy téridő,
amely elsődleges szerepet játszik mint az összes különböző fizikai tevékenység
arénája. Másodszor vannak fizikai objektumok, amelyek
átengedik magukat ennek a tevékenységnek, de pontos matematikai törvényekkel
korlátozottan.
A könyv
matematikai fejezeteiben azt fejtegeti, hogy a matematikát viszont nem
korlátozza a valóság (úgy rémlik ott, ahol Gödelről, a nemteljességről, az
ellentmondásmentességről ír. Ha jól értem a fizikai világban az a valóban
létező, az az igaz, ahol a jelenséget leíró fizika elméletben semmiféle
ellentmondás nem található
A fizikai objektumok kétfélék: részecskék és mezők. A
részecskék valódi természetéről és megkülönböztető jegyeiről kevés szó esik,
tudjuk azt, hogy mindegyiknek van saját világvonala és egyedi (nyugalmi)
tömege, esetleg elektromos töltése stb. A mezők viszont nagyon specifikusak –
az elektromágneses mező a Maxwell-egyenletek tárgya, a gravitációs mező az
Einstein-egyenleteké.
Van bizonyos
kétértelműség abban, hogyan kell a részecskéket kezelni. Azokat, amelyek tömege
olyan kicsi, hogy befolyásuk a mezőkre elhanyagolható, próbarészecskéknek nevezzük
– és ezek mozgása a tereknek adott válaszként egyértelmű. A
Lorentz-erő leírja a próbarészecske válaszát az elektromágneses mezőre, a
geodetikus törvény a választ a gravitációs mezőre (megfelelő kombinációban, ha
mindkét mező jelen van). Ehhez a részecskéket pontszerűeknek, azaz
egydimenziós világvonalúaknak kell tekintenünk. Ha azonban figyelembe kell
vennünk a részecskék hatásait a mezőkre (és így a többi részecskére) – azaz ha
a részecskék forrásai a mezőknek –, akkor térben valamennyire
kiterjedt objektumoknak kell azokat tekintenünk. Máskülönben a mezők minden
részecske közvetlen közelében végtelenné válnak. Ezek a kiterjedt források
szolgáltatják a (ρ, j) töltés–áram-eloszlást, amely a
Maxwell-egyenletekhez, és az ENERGIA tenzort, amely az
Einstein-egyenletekhez szükséges. Mindezekhez járul még, hogy a téridő –
amelyben mind e részecskék és mezők tartózkodnak – változó szerkezetű, ami
önmagában közvetlenül leírja a gravitációt. Az „aréna” csatlakozik a benne
végbemenő történéshez!
Ezt tanította nekünk a
klasszikus fizika a fizikai valóság természetéről. Világos, hogy jó sokat
tanultunk, és az is, hogy nem kell túlságosan önelégülteknek lennünk; a képet,
amelyet valamikor kialakítottunk, későbbi és mélyebb meglátások mindig felboríthatják.
A következő fejezetben látni fogjuk, hogy még a relativitáselmélet által hozott
forradalmi változások is szinte a jelentéktelenségbe szürkülnek a
kvantumelmélet által hozottak mellett.
Mi az „anyag”?
Az a valódi szubsztancia, amelyből a valóságos fizikai objektumok – a világ
„dolgai” – összetevődnek….
Milyen mennyiséggel mérjük
ezt a szubsztanciát? Elemi fizikai tankönyveinkben ott van Newton világos
válasza. Egy objektum vagy objektumrendszer tömege méri a
tartalmazott anyag mennyiségét. Ez valóban helyesnek látszik – nincs más
fizikai mennyiség, amely komolyan versenyezhet a tömeggel, mint a teljes
szubsztancia igazi mértéke. Mi több, ez megmarad: bármilyen
rendszer tömege, és így teljes anyagi tartalma, mindig ugyanaz kell maradjon.
Einstein nevezetes
képlete a speciális relativitáselméletből, az
E = mc2
mégis azt mondja nekünk, hogy a tömeg (m)
és energia (E) átváltoztathatók egymásba. Például amikor egy uránatom
elbomlik, kisebb részekre hasad szét, akkor e részek összes tömege, ha meg
tudnánk mérni, kisebb lenne, mint az uránatom eredeti tömege;
ám ha figyelembe vesszük minden egyes darab mozgásának energiáját –
a kinetikus energiát,106 –
és c2-tel osztva tömegértékké alakítjuk át (mert E = mc2), akkor azt találjuk,
hogy a teljes végösszeg változatlan. A tömeg valóban megmarad,
de mert részben energiából áll, most már kevésbé világos, hogy a valóságos
szubsztancia mértéke. Az energia végül is függ a sebességtől, amellyel a
szubsztancia mozog. Egy expresszvonat mozgási energiája jelentős, de ha úgy
adódik, hogy éppen ezen a vonaton ülünk, akkor saját nézőpontunkból a vonat
egyáltalán nem mozog. A mozgás energiáját (bár az egyes részecskék
véletlenszerű mozgásából származó hőenergiát nem) a nézőpont
alkalmas megválasztásával „nullára csökkentettük”. Egy meglepő példaként, ahol
az Einstein-féle tömeg–energia összefüggés hatása a legszélsőségesebb,
tekintsük a szubatomi részecskék egyik típusának, a π0-mezonnak a bomlását.
Ez biztosan anyagi részecske, jól meghatározott (pozitív)
tömege van. Úgy 10–16 másodperc után szétbomlik (mint előbb az uránatom, csak annál sokkal
gyorsabban) – majdnem mindig két fotonra (5.35. ábra).
A π0-mezonhoz képest nyugvó megfigyelő szerint mindkét foton az energia felét,
és valójában a π0-mezon tömegének felét viszi el. Ez a
„fotontömeg” olyan bizonytalan fajta: tiszta energia. Ha
gyorsan utaznánk az egyik foton irányában, akkor tömeg-energiáját olyan kis
értékre csökkenthetnénk, amilyenre csak akarjuk – lévén egy foton belső tömege
(vagy nyugalmi tömege, mint azt rövidesen tárgyaljuk) nulla. Mindez
hozzájárul a megmaradó tömeg konzisztens képéhez, amely azonban nem egészen az,
mint korábban volt. A tömeg egyfajta értelemben még mindig mérheti az „anyag
mennyiségét”, de a nézőpont világosan megváltozott: mivel a tömeg egyenértékű
az energiával, egy rendszer tömege, az energiához hasonlóan, függ a megfigyelő
mozgásától!
A megmaradó
mennyiség, amely átveszi a tömeg szerepét, egy energia-impulzus négyesvektornak nevezett valami. A Minkowski-tér O kezdőpontjában nyíllal (vektorral)
ábrázolható, O jövőbe mutató fénykúpjának belsejébe (vagy a foton szélsőséges esetében a kúpra) mutat; lásd 5.36. ábra. Ez a nyíl, amely ugyanabba az irányba mutat,
mint az objektum világvonala, minden információt tartalmaz energiájáról,
tömegéről és impulzusáról. Így a nyíl hegyének „t értéke” (vagy „magassága”) valamely megfigyelő
rendszerében mérve megadja az objektum tömegét (vagy c2-tel osztott energiáját) a megfigyelő szerint, míg a térbeli összetevő az impulzust (c-vel osztva).
E nyíl
„Minkowski-hossza” a nyugalmi tömeg néven ismert, fontos
mennyiség, amely a tömeget adja meg az objektumhoz képest nyugvó megfigyelő
számára. Próbálkozhatnánk azzal, hogy ezt válasszuk az
„anyagmennyiség” jó mértékének. Azonban nem additív: ha egy rendszer kétfelé
hasad, akkor az eredeti nyugalmi tömeg nem a két új nyugalmi tömeg összege.
Emlékezzünk a π0-mezon előbb vizsgált bomlására. A π0-mezon nyugalmi tömege
pozitív, míg a keletkező fotonoké nulla. Az egész nyílra (négyesvektorra)
azonban érvényes az additivitási tulajdonság, de most az 5.6. ábrán
bemutatott vektorösszegzési szabály értelmében kell „összeadnunk”.
Most ez a teljes nyíl az „anyag mennyiségére” vonatkozó
mértékünk!
Gondoljunk most
Maxwell elektromágneses mezőjére. Megfigyeltük, hogy energiát hordoz. Az E
= mc2 szerint tömegének is kell lennie. Így Maxwell mezője szintén anyag!
Ezt most biztosan el kell fogadnunk, mert a Maxwell-mezőnek szoros köze van az
erőkhöz, amelyek a részecskéket összetartják. Bármely test tömegéhez lényeges
járulékot107 kell
adjanak a belsejében lévő elektromágneses mezők.
Mi a helyzet Einstein
gravitációs mezőjével? Sok tekintetben Maxwell mezőjére emlékeztet. Hasonlóan
ahhoz, ahogy Maxwell elméletében a mozgó, töltött részecskék elektromágneses hullámokat
tudnak kibocsátani, a mozgó, tömeggel rendelkező testek (Einstein elmélete
szerint) gravitációs hullámokat bocsátanak ki – amelyek, az
elektromágneses hullámokhoz hasonlóan, a fény sebességével terjednek és
energiát hordoznak. Ezt az energiát mégsem a szokásos módon, az ENERGIA tenzorral
mérjük, amelyre korábban utaltam. (Tiszta) gravitációs hullámban ez a tenzor
mindenhol nulla! Mindazonáltal helyezkedhetünk arra a
nézőpontra, hogy valahogy a téridő görbülete (amit most
teljesen a WEYL tenzor ad meg) mutathatja a gravitációs
hullámok „szövedékét”. A gravitációs energia azonban nemlokális, ami
azt jelenti, hogy a téridő görbületének csupán korlátos tartományban való
vizsgálatával nem lehet meghatározni az energia mértékét. A gravitációs mező
energiája – és ezért tömege – sikamlós angolna, nem hagyja magát egy adott
helyen elcsípni. Mindazonáltal komolyan kell venni. Biztosan ott van,
és számításba kell venni, hogy a tömeg általánosan megmaradhasson. Van a
tömegnek egy jó (és pozitív) mértéke (Bondi 1960, Sachs 1962),
amely alkalmazható a gravitációs hullámokra, de a nemlokalitás olyan, hogy ez a
mérték olykor nemzérus lehet a téridő sík tartományaiban
– a sugárzás két hulláma között (hasonlóan, mint a hurrikán magján belüli
csend) –, ahol a téridő teljesen görbületmentes (vö. Penrose és
Rindler 1986, 427. o.), azaz WEYL és RICCI egyaránt zérus!
Ilyen esetekben, úgy látszik, arra kell következtetnünk, hogy ha ez a
tömeg-energia egyáltalán megfogható, akkor ebben a sík üres térben kell
legyen – minden anyagtól vagy mezőtől tökéletesen mentes tartományban. Ilyen
furcsa körülmények között „anyagmennyiségünk” most vagy ott van
az üres tartományok legüresebbjében, vagy egyáltalán nincs sehol!
Ez igazi paradoxonnak
látszik. Mégis határozott velejárója annak, amit legjobb klasszikus elméleteink
– és ezek valóban szuperelméletek – világunk „valóságos” anyagának
természetéről mondanak. Az anyagi valóság a klasszikus elmélet szerint, nem is
beszélve a kvantumelméletről, amelyet éppen kifejteni készülünk, sokkal
ködösebb dolog, mint azt gondoltuk. Mennyiségi meghatározása – sőt hogy vajon
ott van-e vagy sem – határozottan kényes kérdésektől függ, és nem lehet csupán
lokálisan megállapítani! Ha ez a nemlokalitás rejtélyesnek látszik, akkor
készüljünk fel még sokkal nagyobb megrázkódtatásokra.
...Szirénének...
Ez a torzító hatás úgy ismert, mint a gravitáció árapályjelensége. Ha a Föld középpontját a Holddal, a részecskegömböt pedig a Föld felületével helyettesítjük, akkor pontosan előttünk áll a Hold árapályt előidéző hatása, mind a Hold irányában, mind az ellentétes irányban kidagadás jön létre. Az árapályjelenség a gravitációs mezőknek általános tulajdonsága, amelyet szabadeséssel nem lehet „kioltani”. Ez a jelenség a newtoni gravitációs mező nemegyenletességét méri. (Az árapálytorzítás nagysága a vonzócentrumtól mért távolság inverz köbe és nem inverz négyzete szerint csökken.)
Emlékezzünk arra, hogy a
relativitáselméletben az anyagi testek nem mozoghatnak a fénynél gyorsabban –
abban az értelemben, hogy világvonalaiknak mindig a fénykúpokon belül kell
haladniuk (vö. 5.29. ábra).
(Az általános relativitáselméletben a dolgokat ilyen lokális módon kell
megfogalmaznunk. A fénykúpok nem rendeződnek el egyenletesen, így nem volna sok
értelme azt mondani, hogy egy nagyon távoli részecske
sebessége felülmúlja-e az itteni fénysebességet.) A fotonok
világvonalai a fénykúpok mentén fekszenek, de semmilyen
részecske világvonala nem haladhat a kúpokon kívül. Valójában
egy általánosabb állításnak kell igaznak lennie, nevezetesen annak, hogy
semmilyen jel nem mehet a fénykúpon kívül.
Hogy megértsük, miért
kell ennek így lennie, nézzük meg a Minkowski-térről rajzolt képeket (5.31. ábra). Tegyük
fel, hogy készítettünk egy eszközt, amely a fényénél kicsit nagyobb sebességű
jelet képes küldeni. A W megfigyelő jelet küld ezzel az
eszközzel a világvonalán lévő A eseményből egy távoli B eseményhez,
amely valamivel A fénykúpja alatt fekszik. Az 5.31a. ábrán
ezt W nézőpontjából rajzoltuk le, de az 5.31b. ábrán
az egészet újrarajzoltuk egy második, U megfigyelő
nézőpontjából, aki gyorsan távolodik W-től (mondjuk egy A és B közötti
ponttól), és akinek számára a B esemény korábbinak látszik,
mint az A! (Ez az „átrajzolás” egy Poincaré-mozgás, amint azt
korábban már leírtuk.) U egyidejű terei W nézőpontjából
„megbillenteknek” látszanak, ezért láthatja U korábbinak
a B eseményt, mint az A-t. Így a W által
kibocsátott jelet U az időben visszafelé mozgónak látná!
Ez még nem teljesen
ellentmondás. Ám nézzük most a dolgokat U nézőpontjából, szimmetrikusan (a speciális relativitás
elve szerint). Egy harmadik, V megfigyelő U-tól W-vel ellentétes irányban távolodva, ugyanolyan eszközzel
felszerelve, mint W, szintén ki tudna bocsátani egy a fénynél valamivel gyorsabb
jelet az ő (azaz V) nézőpontjából hátrafelé, U irányába. U ezt a jelet is az időben hátrafelé mozgónak látná, most
az ellentétes térbeli irányban. V leadhatna ezt a második jelet W felé hátra abban a pillanatban (B), amikor ő megkapja a W által küldött eredeti jelet. A második jel W-t egy C eseménynél éri el, amely U megítélése szerint korábbi, mint az eredeti kibocsátás A eseménye (5.32. ábra). Ám ennél még rosszabb, hogy a C esemény W saját világvonalán korábbi, mint az A, így W a C esemény bekövetkeztét valójában előbb tapasztalja, mint ahogy A-nál a jelet ő kibocsátja! Az üzenet, amelyet a V megfigyelő visszaküld W-hez, előzetes megegyezés alapján egyszerűen
megismételhetné a B-ben kapott üzenetet. Így W világvonalán korábbi időpontban kapja meg ugyanazt az
üzenetet, mint amelyet ő küld később! A két megfigyelőt elegendően nagy
távolságra szétválasztva elérhető, hogy a visszatérő jel olyan nagy
időkülönbséggel előzze meg az eredeti jelet, amilyennel csak akarjuk. W eredeti üzenete talán az, hogy eltörte a
lábát. A visszaküldött üzenetet még azelőtt megkaphatná, mielőtt a baleset bekövetkezne, és így
(feltehetően) szabad akaratából elkerülhetné azt!
Így a „fénynél
gyorsabb” jeladás és Einstein relativitási elve együtt ordító ellentmondáshoz
vezet normális „szabad akarat” érzésünkkel. A dolog ennél valójában még
komolyabb. Elképzelhetnénk, hogy talán a „W megfigyelő” csupán egy
úgy programozott mechanikus eszköz, hogy „IGEN” üzenetet küldjön, ha „NEM”-et
kap és fordítva. V is lehet mechanikus eszköz, de úgy
programozva, hogy ha „NEM”-et kap, küldje vissza a „NEM”-et, ha „IGEN”-t kap,
küldje vissza az „IGEN”-t. Ez ugyanahhoz a lényeges ellentmondáshoz vezet,
amelyet az előbb láttunk,102 most
látszólag függetlenül attól a kérdéstől, van-e vagy nincs a W megfigyelőnek
„szabad akarata”, és azt mondja nekünk, hogy egy fénynél gyorsabb jelet
kibocsátó eszköz „nem működhet” mint fizikai lehetőség. Ennek a későbbiekben
még lesznek rejtélyes következményei (6. fejezet).
Fogadjuk tehát el,
hogy semmiféle jel – nem csupán a közönséges fizikai
részecskék által hordozottak – nem kerülhet a fénykúpokon kívülre. Az előző
érvelés a speciális relativitást használja, de a speciális
elmélet szabályai lokálisan érvényesek maradnak az általános
relativitáselméletben. A speciális relativitás lokális érvényessége mondja azt,
hogy a fénykúpok magukba zárnak minden jelet, ezért ez igaz kell legyen az
általános elméletben is. Látni fogjuk, hogyan befolyásolja ez a determinizmus kérdését
ezekben az elméletekben. Emlékezzünk vissza, hogy a newtoni (vagy hamiltoni
stb.) rendszerben a „determinizmus” azt jelenti, hogy „egy speciális
időpontbeli kezdeti adatok” teljesen meghatározzák a viselkedést minden más
időpontban. Ha a newtoni elméletben téridő-leírásmódot alkalmazunk, a
„speciális időpont”, amelyben az adatokat előírjuk, a négydimenziós téridő
valamely háromdimenziós „metszete” volna (azaz az egész tér abban az egy
időpontban). A relativitáselméletben nincs globális „idő”, ami erre a célra
kiválasztható volna. A szokásos eljárás az, hogy rugalmasabb hozzáállást
fogadunk el. Bárki „ideje” megteszi. A speciális relativitáselméletben a
kezdeti adatok előírására az előbbi „metszetnek” bármelyik megfigyelő egyidejű
terét vehetjük. Az általános relativitáselméletben azonban az „egyidejű tér”
fogalom nem jól meghatározott. Helyette a térszerű felület általánosabb
fogalmát használhatjuk.103
A speciális relativitáselméletben a
determinizmus úgy fogalmazható meg, hogy a tetszőlegesen adott S egyidejű téren rögzített kezdeti adatok
meghatározzák a viselkedést az egész téridőben. (Ez a Maxwell-elméletre is
igaz, amely valójában „speciális-relativisztikus” elmélet.) Lehet azonban
erősebb állítást is tenni. Ha tudni akarjuk, mi fog történni az S jövőjében fekvő valamely P eseménynél, ahhoz a kezdeti adatokat nem
kell az egész S-ben tudnunk, csak egy korlátos (véges) tartományában. Ennek
oka az, hogy az „információ” nem terjedhet gyorsabban, mint a fény, így S-nek azok a pontjai, amelyek túl messze fekszenek
ahhoz, hogy belőlük fényjel érje el P-t, nem lehetnek hatással P-re (lásd az 5.34. ábrát).104 Ez sokkal kielégítőbb, mint a newtoni
esetben létrejövő helyzet, ahol elvileg tudnunk kellene, mi történt a teljes végtelen „metszeten”, hogy egyáltalán jóslatot
tehessünk, mi fog történni tetszőleges pontban egy pillanattal később. Nincs
megszorítás arra, milyen sebességgel terjedhet a newtoni információ, a newtoni
erők valójában pillanatszerűek.
A „determinizmus” az általános relativitáselméletben jóval bonyolultabb dolog, mint a speciálisban, és csak néhány megjegyzést fogok ezzel kapcsolatban tenni. Elsősorban egy S térszerű felületet (és nem egyidejű felületet) kell használnunk a kezdeti adatok előírására. Ekkor az a helyzet, hogy az Einstein-egyenletek a gravitációs mező lokálisan determinisztikus viselkedését adják, feltéve (mint szokásosan), hogy az ENERGIA tenzorhoz járulékot adó anyagmezők determinisztikusan viselkednek. Vannak azonban jelentős bonyodalmak. Maga a téridő geometriája – fénykúp „kauzalitás”-szerkezetével együtt – most része annak, ami ténylegesen meghatározásra kerül. E fénykúpszerkezetet időben előre nem ismerjük, így nem tudjuk megmondani, S mely részeire van szükség, hogy meghatározzuk a viselkedést egy jövőbeli P eseménynél. Bizonyos szélsőséges esetekben előfordulhat, hogy az egész S sem elegendő, következésképpen a globális determinizmus elvész! (Nehéz kérdések kerülnek itt elő, és az általános relativitáselmélet egy fontos megoldatlan problémájához, az ún. „kozmikus cenzúrához” kapcsolódnak – aminek köze van a fekete lyukak létrejöttéhez (Tipler és mások 1980; vö. 7. fejezet) Nagyon valószínűtlennek látszik, hogy a „szélsőséges” gravitációs mezőknél esetleg bekövetkező, bármiféle „determinizmuskudarcnak” közvetlen hatása volna az emberi skálájú dolgokra,...de azért ez a hiány, nem teljesség, nem teljes érvényesség nyugtalanítja Penroset.
Kiszámíthatóság a
klasszikus fizikában: hogyan is állunk?
E fejezetben végig próbáltam szemmel tartani
a kiszámíthatóság kérdését, mint ami különbözik a
determinizmusétól, és próbáltam jelezni, hogy amikor a „szabad akarat” és a
szellemi jelenségek kérdéseit tárgyaljuk, akkor a kiszámíthatósági problémák
legalább annyira fontosak, mint a determinizmus. Kiderült azonban, hogy a
determinizmus önmagában sem egészen olyan világos a klasszikus elméletben, mint
ahogy azt elhitették velünk. Láttuk, hogy a töltött részecske mozgásának
klasszikus Lorentz-egyenlete zavaró problémákat vet fel. (Emlékezzünk Dirac „elfutó
megoldásaira”.) Észrevettük azt is, hogy a determinizmussal az általános
relativitáselméletben is vannak nehézségek. Amikor az ilyen elméletekben nincs
determinizmus, akkor bizonyára nincs kiszámíthatóság sem. Mégis, egyik
felidézett esetben sem látszik úgy, hogy a determinizmus hiányának számottevő
közvetlen filozófiai jelentősége volna számunkra. Szabad akaratunk számára még
nincs „hely” ezekben a jelenségekben: az első esetben azért, mert úgy
gondoljuk, hogy pontszerű részecskére a klasszikus Lorentz-egyenlet (ahogy
Dirac megoldotta) fizikailag nem megfelelő azon a szinten, ahol ezek a
problémák fellépnek; a másodikban azért, mert azok a skálák, ahol a klasszikus
általános relativitáselmélet ilyen problémákhoz vezethet (fekete lyukak stb.),
teljesen eltérőek agyunk skáláitól.
Hogy állunk akkor most
a kiszámíthatósággal a klasszikus elméletben? Ésszerű az a
sejtés, hogy az általános relativitáselmélet helyzete nem különbözik jelentősen
a speciálisétól – túl a kauzalitásban és a determinizmusban lévő különbségeken,
amelyekről éppen az előbb beszéltem. Ahol a fizikai rendszer jövőbeli
viselkedését a kezdeti adatok meghatározzák, ott ez a jövőbeli viselkedés (hasonló
okokból, mint amelyeket a newtoni elméletnél kifejtettem) az adatok által kiszámíthatóan meghatározottnak
látszik105 (eltekintve
a nemkiszámíthatóságnak attól a „nem éppen segítőkész” típusától, amelyet
Pour-El és Richards a hullámegyenletnél találtak – és amely folytonosan változó
adatok mellett nem lép fel). Valójában nehéz látni, hogy bármelyik eddig
megvizsgált fizikai elméletben lehetnének jelentős „nem kiszámítható” elemek.
Azt biztosan várnunk kell, hogy az elméletek közül sokban bekövetkezhet az a
„kaotikus” viselkedés, amikor nagyon kis változások a kezdeti adatokban
hatalmas különbségeket okozhatnak az eredő viselkedésben. (Ez a helyzet látszik
az általános relativitásban, vö. Misner 1969, Belinskii és
mások 1970.) De amint az előbb említettem, nehéz azt látni, hogy a
nemkiszámíthatóságnak ez a fajtája – azaz a „jósolhatatlanság”
– bármilyen „hasznára” lehet egy eszköznek, amely megpróbálja „kiaknázni” a
fizikai törvényekben lévő lehetséges nem kiszámítható elemeket. Ha az „értelem”
bármiképp hasznosíthatja ezeket, akkor úgy látszik, a klasszikus fizikán kívül
kell lenniük ezeknek az elemeknek. E kérdést később újra meg kell vizsgálnunk,
miután már vetettünk egy pillantást a kvantumelméletre.
.........
1./
Szabad akaratunk számára még nincs
„hely” ezekben a jelenségekben: az első esetben azért, mert úgy gondoljuk, hogy
pontszerű részecskére a klasszikus Lorentz-egyenlet (ahogy Dirac megoldotta)
fizikailag nem megfelelő azon a szinten, ahol ezek a problémák fellépnek; a
másodikban azért, mert azok a skálák, ahol a klasszikus általános
relativitáselmélet ilyen problémákhoz vezethet (fekete lyukak stb.), teljesen
eltérőek agyunk skáláitól. - írja.
…teljesen eltérőek agyunk skáláitól…és előtte zárójelben, hogy például hol uralkodnak azok az eltérő
skálák (fekete lyukak
stb.)
Többször felvillantja azt, amit a magamfajta halandó szeretne
elkapni, hiú remény, hogy megérteni, csak elkapni, vagy legalábbis megérinteni.
Egy régen olvasott- elég jó –
fantasztikus regényben egy űrhajót magába ránt egy fekete lyuk. Öten vagy hatan
utaztak a hajón. A könyv utolsó oldalának történései már a „szingularitáson”
túlról szólnak: az események helyszíne ott a lyuk túloldalán nem a túlvilág, és
nem is az a klinikai halálból visszatértek emlékidézéseiben derengő gyöngyház-szín
szórású, sejtelmes, békés, hívogató fény (nagyon szeretem Kandinszkij: A fény,
amely nem okoz fájdalmat című festményét); nem, ez a valami ahová az került ami
valaha a hajó és utasai voltak, ez egy az elemei közötti kapcsolatot,
párbeszédet, egymás érzékelését lehetővé tevő környezet…és az űrhajósok, vagyis
azok a még szubatomi részecskékhez sem hasonlítható valamik, amik belőlük
maradtak, csodálva érzékelik a helyet, a helyzetet, ezt a gyöngyházfény –világot,
és rögtön közlik is „egymással”, amit „átélnek”, „éreznek”, „érzékelnek”, „észlelnek”
és „látnak”.
2./
De amint az előbb említettem, nehéz azt
látni, hogy a nemkiszámíthatóságnak ez a fajtája – azaz a
„jósolhatatlanság” – bármilyen „hasznára” lehet egy eszköznek, amely
megpróbálja „kiaknázni” a fizikai törvényekben lévő lehetséges nem kiszámítható
elemeket. Ha az „értelem” bármiképp hasznosíthatja ezeket, akkor úgy látszik, a
klasszikus fizikán kívül kell lenniük ezeknek az elemeknek. E kérdést később
újra meg kell vizsgálnunk, miután már vetettünk egy pillantást a
kvantumelméletre.
…
… Ha az „értelem” bármiképp hasznosíthatja ezeket,
akkor úgy látszik, a klasszikus fizikán kívül kell lenniük ezeknek az elemeknek…
…
„értelem”
…
’a valami bennünk ül és figyel’
– kapisgáltam ezt valamikor negyedikes gimnazista koromban egy írásomban.
„Én túllépek e mai kocsmán,
az értelemig és tovább!” [József Attila]
Tömeg, anyag és
valóság
Tekintsük röviden át a világnak azt a
képét, amelyet a klasszikus fizika nyújt számunkra. Először is van egy téridő,
amely elsődleges szerepet játszik mint az összes különböző fizikai tevékenység
arénája. Másodszor vannak fizikai objektumok, amelyek
átengedik magukat ennek a tevékenységnek, de pontos matematikai törvényekkel
korlátozottan.
A könyv
matematikai fejezeteiben azt fejtegeti, hogy a matematikát viszont nem
korlátozza a valóság (úgy rémlik ott, ahol Gödelről, a nemteljességről, az
ellentmondásmentességről ír. Ha jól értem a fizikai világban az a valóban
létező, az az igaz, ahol a jelenséget leíró fizika elméletben semmiféle
ellentmondás nem található
A fizikai objektumok kétfélék: részecskék és mezők. A
részecskék valódi természetéről és megkülönböztető jegyeiről kevés szó esik,
tudjuk azt, hogy mindegyiknek van saját világvonala és egyedi (nyugalmi)
tömege, esetleg elektromos töltése stb. A mezők viszont nagyon specifikusak –
az elektromágneses mező a Maxwell-egyenletek tárgya, a gravitációs mező az
Einstein-egyenleteké.
Van bizonyos
kétértelműség abban, hogyan kell a részecskéket kezelni. Azokat, amelyek tömege
olyan kicsi, hogy befolyásuk a mezőkre elhanyagolható, próbarészecskéknek nevezzük
– és ezek mozgása a tereknek adott válaszként egyértelmű. A
Lorentz-erő leírja a próbarészecske válaszát az elektromágneses mezőre, a
geodetikus törvény a választ a gravitációs mezőre (megfelelő kombinációban, ha
mindkét mező jelen van). Ehhez a részecskéket pontszerűeknek, azaz
egydimenziós világvonalúaknak kell tekintenünk. Ha azonban figyelembe kell
vennünk a részecskék hatásait a mezőkre (és így a többi részecskére) – azaz ha
a részecskék forrásai a mezőknek –, akkor térben valamennyire
kiterjedt objektumoknak kell azokat tekintenünk. Máskülönben a mezők minden
részecske közvetlen közelében végtelenné válnak. Ezek a kiterjedt források
szolgáltatják a (ρ, j) töltés–áram-eloszlást, amely a
Maxwell-egyenletekhez, és az ENERGIA tenzort, amely az
Einstein-egyenletekhez szükséges. Mindezekhez járul még, hogy a téridő –
amelyben mind e részecskék és mezők tartózkodnak – változó szerkezetű, ami
önmagában közvetlenül leírja a gravitációt. Az „aréna” csatlakozik a benne
végbemenő történéshez!
Ezt tanította nekünk a
klasszikus fizika a fizikai valóság természetéről. Világos, hogy jó sokat
tanultunk, és az is, hogy nem kell túlságosan önelégülteknek lennünk; a képet,
amelyet valamikor kialakítottunk, későbbi és mélyebb meglátások mindig felboríthatják.
A következő fejezetben látni fogjuk, hogy még a relativitáselmélet által hozott
forradalmi változások is szinte a jelentéktelenségbe szürkülnek a
kvantumelmélet által hozottak mellett.
Mi az „anyag”?
Az a valódi szubsztancia, amelyből a valóságos fizikai objektumok – a világ
„dolgai” – összetevődnek….
Milyen mennyiséggel mérjük
ezt a szubsztanciát? Elemi fizikai tankönyveinkben ott van Newton világos
válasza. Egy objektum vagy objektumrendszer tömege méri a
tartalmazott anyag mennyiségét. Ez valóban helyesnek látszik – nincs más
fizikai mennyiség, amely komolyan versenyezhet a tömeggel, mint a teljes
szubsztancia igazi mértéke. Mi több, ez megmarad: bármilyen
rendszer tömege, és így teljes anyagi tartalma, mindig ugyanaz kell maradjon.
Einstein nevezetes
képlete a speciális relativitáselméletből, az
E = mc2
mégis azt mondja nekünk, hogy a tömeg (m)
és energia (E) átváltoztathatók egymásba. Például amikor egy uránatom
elbomlik, kisebb részekre hasad szét, akkor e részek összes tömege, ha meg
tudnánk mérni, kisebb lenne, mint az uránatom eredeti tömege;
ám ha figyelembe vesszük minden egyes darab mozgásának energiáját –
a kinetikus energiát,106 –
és c2-tel osztva tömegértékké alakítjuk át (mert E = mc2), akkor azt találjuk,
hogy a teljes végösszeg változatlan. A tömeg valóban megmarad,
de mert részben energiából áll, most már kevésbé világos, hogy a valóságos
szubsztancia mértéke. Az energia végül is függ a sebességtől, amellyel a
szubsztancia mozog. Egy expresszvonat mozgási energiája jelentős, de ha úgy
adódik, hogy éppen ezen a vonaton ülünk, akkor saját nézőpontunkból a vonat
egyáltalán nem mozog. A mozgás energiáját (bár az egyes részecskék
véletlenszerű mozgásából származó hőenergiát nem) a nézőpont
alkalmas megválasztásával „nullára csökkentettük”. Egy meglepő példaként, ahol
az Einstein-féle tömeg–energia összefüggés hatása a legszélsőségesebb,
tekintsük a szubatomi részecskék egyik típusának, a π0-mezonnak a bomlását.
Ez biztosan anyagi részecske, jól meghatározott (pozitív)
tömege van. Úgy 10–16 másodperc után szétbomlik (mint előbb az uránatom, csak annál sokkal
gyorsabban) – majdnem mindig két fotonra (5.35. ábra).
A π0-mezonhoz képest nyugvó megfigyelő szerint mindkét foton az energia felét,
és valójában a π0-mezon tömegének felét viszi el. Ez a
„fotontömeg” olyan bizonytalan fajta: tiszta energia. Ha
gyorsan utaznánk az egyik foton irányában, akkor tömeg-energiáját olyan kis
értékre csökkenthetnénk, amilyenre csak akarjuk – lévén egy foton belső tömege
(vagy nyugalmi tömege, mint azt rövidesen tárgyaljuk) nulla. Mindez
hozzájárul a megmaradó tömeg konzisztens képéhez, amely azonban nem egészen az,
mint korábban volt. A tömeg egyfajta értelemben még mindig mérheti az „anyag
mennyiségét”, de a nézőpont világosan megváltozott: mivel a tömeg egyenértékű
az energiával, egy rendszer tömege, az energiához hasonlóan, függ a megfigyelő
mozgásától!
A megmaradó
mennyiség, amely átveszi a tömeg szerepét, egy energia-impulzus négyesvektornak nevezett valami. A Minkowski-tér O kezdőpontjában nyíllal (vektorral)
ábrázolható, O jövőbe mutató fénykúpjának belsejébe (vagy a foton szélsőséges esetében a kúpra) mutat; lásd 5.36. ábra. Ez a nyíl, amely ugyanabba az irányba mutat,
mint az objektum világvonala, minden információt tartalmaz energiájáról,
tömegéről és impulzusáról. Így a nyíl hegyének „t értéke” (vagy „magassága”) valamely megfigyelő
rendszerében mérve megadja az objektum tömegét (vagy c2-tel osztott energiáját) a megfigyelő szerint, míg a térbeli összetevő az impulzust (c-vel osztva).
E nyíl
„Minkowski-hossza” a nyugalmi tömeg néven ismert, fontos
mennyiség, amely a tömeget adja meg az objektumhoz képest nyugvó megfigyelő
számára. Próbálkozhatnánk azzal, hogy ezt válasszuk az
„anyagmennyiség” jó mértékének. Azonban nem additív: ha egy rendszer kétfelé
hasad, akkor az eredeti nyugalmi tömeg nem a két új nyugalmi tömeg összege.
Emlékezzünk a π0-mezon előbb vizsgált bomlására. A π0-mezon nyugalmi tömege
pozitív, míg a keletkező fotonoké nulla. Az egész nyílra (négyesvektorra)
azonban érvényes az additivitási tulajdonság, de most az 5.6. ábrán
bemutatott vektorösszegzési szabály értelmében kell „összeadnunk”.
Most ez a teljes nyíl az „anyag mennyiségére” vonatkozó
mértékünk!
Gondoljunk most
Maxwell elektromágneses mezőjére. Megfigyeltük, hogy energiát hordoz. Az E
= mc2 szerint tömegének is kell lennie. Így Maxwell mezője szintén anyag!
Ezt most biztosan el kell fogadnunk, mert a Maxwell-mezőnek szoros köze van az
erőkhöz, amelyek a részecskéket összetartják. Bármely test tömegéhez lényeges
járulékot107 kell
adjanak a belsejében lévő elektromágneses mezők.
Mi a helyzet Einstein
gravitációs mezőjével? Sok tekintetben Maxwell mezőjére emlékeztet. Hasonlóan
ahhoz, ahogy Maxwell elméletében a mozgó, töltött részecskék elektromágneses hullámokat
tudnak kibocsátani, a mozgó, tömeggel rendelkező testek (Einstein elmélete
szerint) gravitációs hullámokat bocsátanak ki – amelyek, az
elektromágneses hullámokhoz hasonlóan, a fény sebességével terjednek és
energiát hordoznak. Ezt az energiát mégsem a szokásos módon, az ENERGIA tenzorral
mérjük, amelyre korábban utaltam. (Tiszta) gravitációs hullámban ez a tenzor
mindenhol nulla! Mindazonáltal helyezkedhetünk arra a
nézőpontra, hogy valahogy a téridő görbülete (amit most
teljesen a WEYL tenzor ad meg) mutathatja a gravitációs
hullámok „szövedékét”. A gravitációs energia azonban nemlokális, ami
azt jelenti, hogy a téridő görbületének csupán korlátos tartományban való
vizsgálatával nem lehet meghatározni az energia mértékét. A gravitációs mező
energiája – és ezért tömege – sikamlós angolna, nem hagyja magát egy adott
helyen elcsípni. Mindazonáltal komolyan kell venni. Biztosan ott van,
és számításba kell venni, hogy a tömeg általánosan megmaradhasson. Van a
tömegnek egy jó (és pozitív) mértéke (Bondi 1960, Sachs 1962),
amely alkalmazható a gravitációs hullámokra, de a nemlokalitás olyan, hogy ez a
mérték olykor nemzérus lehet a téridő sík tartományaiban
– a sugárzás két hulláma között (hasonlóan, mint a hurrikán magján belüli
csend) –, ahol a téridő teljesen görbületmentes (vö. Penrose és
Rindler 1986, 427. o.), azaz WEYL és RICCI egyaránt zérus!
Ilyen esetekben, úgy látszik, arra kell következtetnünk, hogy ha ez a
tömeg-energia egyáltalán megfogható, akkor ebben a sík üres térben kell
legyen – minden anyagtól vagy mezőtől tökéletesen mentes tartományban. Ilyen
furcsa körülmények között „anyagmennyiségünk” most vagy ott van
az üres tartományok legüresebbjében, vagy egyáltalán nincs sehol!
Ez igazi paradoxonnak
látszik. Mégis határozott velejárója annak, amit legjobb klasszikus elméleteink
– és ezek valóban szuperelméletek – világunk „valóságos” anyagának
természetéről mondanak. Az anyagi valóság a klasszikus elmélet szerint, nem is
beszélve a kvantumelméletről, amelyet éppen kifejteni készülünk, sokkal
ködösebb dolog, mint azt gondoltuk. Mennyiségi meghatározása – sőt hogy vajon
ott van-e vagy sem – határozottan kényes kérdésektől függ, és nem lehet csupán
lokálisan megállapítani! Ha ez a nemlokalitás rejtélyesnek látszik, akkor
készüljünk fel még sokkal nagyobb megrázkódtatásokra.
...Szirénének...
6. Kvantumvarázslatok, kvantumtitkok
Kell-e a
filozófusoknak a kvantumelmélet?
A klasszikus fizikában a józan ésszel
összhangban „ott kint” van egy objektív világ. Ez világos és determinisztikus
módon fejlődik, pontosan megfogalmazott matematikai egyenletek kormányozzák.
Egyformán igaz ez Maxwell és Einstein elméleteire, és az eredeti newtoni
rendszerre. A fizikai valóság tőlünk függetlenül létezik; és hogy pontosan
milyen a klasszikus világ, azt nem befolyásolja az, hogy mi hogyan nézünk rá.
Mi több, testünk és agyunk szintén része ennek a világnak. A klasszikus
fizikában ezek is ugyanazon pontos és determinisztikus, klasszikus egyenletek
szerint fejlődnek. Minden cselekedetünket ezek az egyenletek szabják meg –
függetlenül attól, hogy esetleg úgy érezzük, tudatos akaratunk befolyásolhatja
viselkedésünket.
Ez a kép az alapja a
valóság, valamint a tudatos érzékelésünk és nyilvánvaló szabad akaratunk
természetével foglalkozó legkomolyabb108 filozófiai
érvrendszereknek. Egyeseknek meglehet az a kényelmetlen érzése, hogy szerepe
kell legyen a kvantumelméletnek is – a dolgok ezen alapvető,
de sok zavart okozó rendszerének, amely a világ tényleges viselkedése és a
klasszikus fizika által szolgáltatott leírás közötti finom eltérésekből nőtt ki
századunk első negyedében. A „kvantumelmélet” szó sokakban csupán egy „határozatlansági
elv” homályos fogalmát ébreszti fel, amely a részecskék, atomok vagy molekulák
szintjén leírásainkban megtiltja a pontosságot, csak valószínűségi viselkedést
engedélyez. A kvantumos leírások, mint látni fogjuk, valójában nagyon pontosak,
bár a megszokott klasszikusaktól radikálisan különböznek. Mi több, éppen egy
általános nézet ellenkezőjét fogjuk találni, azt, hogy a valószínűségek nem a
részecskék, atomok vagy molekulák parányi kvantumszintjén lépnek fel –
azok determinisztikusam fejlődnek –, hanem látszólag valami
titokzatos, nagyléptékű hatás következtében, összefüggésben a tudatosan
érzékelt klasszikus világ megjelenésével. Meg kell próbálnunk megérteni ezt, és
azt is, hogyan kényszerít bennünket a kvantumelmélet, hogy megváltoztassuk a
fizikai valóságról alkotott képünket.
Hajlamosak vagyunk azt
hinni, hogy a kvantumos és a klasszikus elméletek közötti eltérések nagyon
csekélyek, ám valójában ezek állnak sok, közönséges léptékű fizikai jelenség
hátterében. A szilárd testek puszta létezése, az anyagok szilárdsága és más
fizikai tulajdonságai, a kémia egész természete, a tárgyak színe, a fagyás és
forrás jelensége, az öröklődés megbízhatósága – és sok más megszokott
tulajdonság magyarázatát a kvantumelmélet adja meg. Talán a tudatosság is olyan
jelenség, amely nem érthető meg csak klasszikus fogalmak alapján. Talán
értelmünk is olyan minőség, amely sokkal inkább a világunkat kormányzó fizikai
törvények különös és csodálatos tulajdonságaiban gyökerezik, és nem egy klasszikus fizikai
szerkezet ún. „objektumai” által végrehajtott algoritmus egy tulajdonsága.
Talán bizonyos értelemben ez az, „amiért” nekünk, érző lényeknek kvantumos
világban kell élnünk, és nem teljesen klasszikusban, utóbbi minden gazdagsága
és igazi titokzatossága ellenére. Lehet-e olyannak megkövetelni a
kvantumos világot, hogy anyagából felépíthetők legyenek gondolkodó, érző
teremtmények, mint mi magunk? Ezt a kérdést sokkal inkább egy benépesített
világegyetemet teremteni szándékozó Istennek kell feltenni, nem magunknak! Ám
bennünket is lényegesen érint. Ha a klasszikus világnak nem lehet része a
tudatosság, akkor értelmünk valamilyen módon a klasszikus fizikától való
speciális eltérésekre kell hogy támaszkodjon. Erre a gondolatra később majd még
visszatérek.
Ha mélyre akarunk ásni
a filozófia egyes fontos kérdéseiben, akkor valóban a kvantumelmélethez – a
fizikai elméletek e legegzaktjábbhoz és legtitokzatosabbjához – kell
fordulnunk: hogyan viselkedik világunk, és mi alkotja az „értelmet”, amely
valójában „mi” vagyunk? Mégis a tudomány egy nap majd a Természet még mélyebb megértését
adhatja, mint amilyet a kvantumelmélet nyújtani tud. Személyes véleményem az,
hogy még a kvantumelmélet is csak átmeneti megoldás, bizonyos lényeges
dolgokban nem tud teljes képet adni világunkról, amelyben élünk. De ez nem ad
felmentést; ha valamelyes filozófiai bepillantást akarunk szerezni, akkor meg
kell ismernünk a világ képét a létező kvantumelmélet szerint.
Sajnos, a különböző
elméletek nagyon különböző (bár a megfigyelhetőket tekintve ekvivalens)
nézeteket vallanak e kép aktualitásáról. Sokan, akik a
kvantumelmélet egyik központi alakját, Niels Bohrt követik, azt mondják, hogy
objektív kép egyáltalán nincs is. A kvantumszinten valójában
nincs semmi „ott kinn”. A valóság csak a „mérések” eredményeivel kapcsolatban
merül fel. E nézet szerint a kvantumelmélet csupán számítási eljárást kínál, és
nem szándékozik leírni a világot, amilyen az valójában. Az elmélethez való
ilyen hozzáállás, nekem úgy tetszik, túlságosan kishitű, magam a pozitívabb
vonalat követem, amely a kvantumos leírásnak objektív fizikai valóságot tulajdonít:
a kvantumállapotot.
Van egy nagyon pontos
egyenlet, a Schrödinger-egyenlet, amely tökéletesen
determinisztikus időfejlődését adja ennek az állapotnak. Nagyon különös viszony
van azonban az időfejlesztett kvantumállapot és a fizikai világ megfigyelt
viselkedése között. Időről időre – amikor csak úgy véljük, hogy egy „mérés”
bekövetkezett – majdnem el kell dobnunk azt a kvantumállapotot, amelyet
fáradságosan fejlesztettünk, csak a különböző valószínűségek számítására
használhatjuk, amelyekkel az állapot új lehetséges állapotok
egy sorozatának egyikébe vagy másikába „átugrik”. E „kvantumugrás”
furcsaságához jön még az a probléma, hogy meg kell határoznunk, milyen az a
fizikai berendezés, amely kijelenti, hogy megtörtént egy „mérés”. A
mérőkészülék maga is feltételezhetően kvantumos összetevőkből épül fel, és így
a determinisztikus Schrödinger-egyenlet szerint fejlődik. Szükséges-e tudatos
lény jelenléte ahhoz, hogy egy „mérés” ténylegesen megtörténjék?
Azt hiszem, a kvantumfizikusoknak csak elenyésző kisebbsége felelne igennel.
Feltehetően maguk az emberi megfigyelők is parányi kvantumos alkotórészekből
állnak!
Itt jó
pár mondatban ismerteti miről lesz szó a hatodik fejezetben…többek között:
Meg fogjuk részletesen
vizsgálni a spin különös (és alapvetően kvantummechanikai)
tulajdonságát. Megtárgyaljuk a „Schrödinger macskája” paradox gondolatkísérlet
által felvetett fontos kérdéseket és az elméletiek különböző nézeteit, amelyek
részben e nagyon alapvető rejtély megoldására irányulnak.
Spin: ott volt a negyedikes kémia könyvünkben, de én „disznó” , lusta
diákként – mivel a két szaktárgyunk közül érettségire a biológiát választottam –
akkor nem érdeklődtem különösebben a spin és az atomfizika iránt…
E fejezet egyes részei
nem emészthetők annyira könnyen, mint az előző (vagy következő) fejezetek
anyaga, és olykor kissé technikaiak. Leírásomban próbáltam nem csalni, és egy
kicsit keményebben kell majd dolgoznunk, mint egyébként, hogy valamennyire
megérthessük a kvantumos világot. Tanácsolom az Olvasónak, folytassa akkor is,
ha egy érv homályos marad, próbáljon a szerkezet egészének ízére ráérezni. Ne
keseredjen el akkor sem, ha a teljes megértés nem sikerül. Ez magának a
tárgykörnek a természetéből ered!
Mint Moldova csodacsatára az Idegen bajnok-ban én is lehajolok és megkötöm rendesem a futballcipőm fűzőjét, nehogy leessen miközben megkísérlem a kissé nehéznek igérkező utolsó akciót (itt a megértést) végrehajtani.

















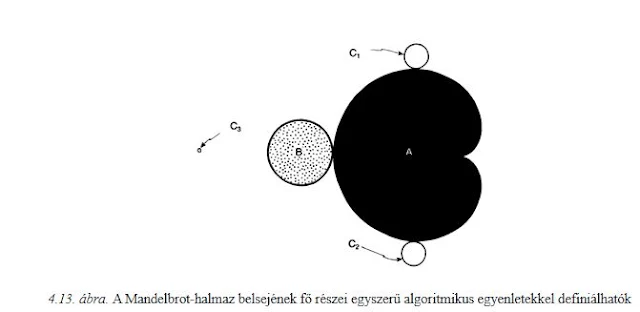





























Megjegyzések
Megjegyzés küldése