Átmenet egyikből a másikba
Ternészettudomány-tagozatos osztály voltunk. Sok felfedezés a kémiában a fizikában vagy a biológiában alig pár évvel előzte meg gimnáziumi éveinket. Az ilyenfajta felfedezések, alapvető átalakulások, vagy nevezhetjük "forradalmi" változásoknak is, a művészeti ágakban - ama négy évünknél - jóval előbb és jóval később történtek. (ez utóbbi megállapítás természetesen vitatható, kicsi és savanyú is, de saját
"kútfőmből" származó)
Sok neves matematikus és fizikus találja nehéznek, ha nem lehetetlennek, hogy olyan könyvet írjon, amelyet a nem szakmabeliek is megérthetnek.
Penrose munkái közepette időt szakított magának, és egy csodálatos könyvet írt a tájékozott laikusok számára.
A könyvből kiderül, hogy Penrose több, mint matematikai fizikus. Elsőrangú filozófus is, aki nem fél olyan problémákkal megküzdeni, amelyeket a kortárs filozófusok mint értelmetleneket hajlamosak elutasítani.
Megvan a bátorsága ahhoz is, hogy a fizikusok egy kis csoportjának növekvő ellenállása ellenére elkötelezze magát az egészséges realizmus mellett. Nemcsak arról van szó, hogy a világegyetem „ott kint” van, hanem hogy a matematikai igazságnak is megvan a saját titokzatos függetlensége és időtlensége. Mint Newton és Einstein, Penrose is mély alázattal és tisztelettel fordul mind a fizikai világ, mind a tiszta matematika platóni birodalma felé. Erdős Pál, a számelmélet kiváló művelője „Isten könyvét” szereti emlegetni, amelyben a legjobb bizonyítások mind fel vannak jegyezve. Egyes matematikusok olykor egy pillantást vethetnek egy lap töredékére. Penrose úgy véli, hogy amikor egy fizikusnak vagy matematikusnak egy hirtelen „aha” élményben van része, akkor az több, mint valamilyen „bonyolult számítás gyümölcse”. Egy pillanatra az értelem lép ekkor kapcsolatba az objektív igazsággal. Lehet-e, kérdezi Penrose, hogy Platón világa és a fizikai világ (amelyet a fizikusok már beolvasztottak a matematikába) tulajdonképpen egy és ugyanaz?
Penrose könyve sok oldalt szentel a nevezetes, felfedezőjéről, Benoit Mandelbrotról Mandelbrot-halmaznak elnevezett, fraktálszerű szerkezetnek. Noha ez statisztikus értelemben önhasonló, mert egyes részei nagyítódnak ki, végtelenül tekervényes mintája megjósolhatatlan módon változik. Penrose (velem együtt) elképzelhetetlennek tartja, hogy bárki azt gondolja, hogy ez az egzotikus rendszer nincs annyira „ott kint”, mint a Mount Everest, hogy ne olyan felfedezés tárgya legyen, mint például egy dzsungel."
...
Van-e egy szint a kvantummechanika fölött, amelybe az idő iránya és a jobb és a bal megkülönböztetése határozottan be van ágyazva? Lényegesek-e az értelem működése számára a kvantummechanika törvényei, vagy esetleg még elemibb törvények?
A két utolsó kérdésre Penrose igennel válaszol. Nevezetes elmélete a „twisztorokról” – a téridő alapjául szolgáló magasabb dimenziós, komplex térben működő, absztrakt geometriai objektumokról – túlságosan szakmai jellegű ahhoz, hogy benne lehessen ebben a könyvben. Penrose több mint két évtizede törekszik arra, hogy a kvantummechanika mezőinél és részecskéinél mélyebb tartományba ásson le. Háromféle osztályba sorolja az elméleteket, ezek a szuper, a hasznos és a kísérleti, és a twisztorelméletet szerényen a kísérleti osztályba teszi, a mostanában hevesen vitatott szuperhúrok és más nagy egyesítési rendszerek mellé."
"Penrose eredményei a matematikában és a fizikában – amelyeknek csak kis töredékét érintettem – a létezés titka és szépsége iránti, egész életen át tartó kíváncsiság szüleményei. Kisujja azt mondja neki, hogy az emberi elme több, mint parányi huzalok és kapcsolók puszta gyűjteménye. A prológus és epilógus Adamja részben szimbóluma a tudatosság hajnalának az érzelmi élet lassú fejlődésében. Számomra ő is Penrose – a gyermek a harmadik sorban, a MI élharcosai mögött –, aki ki meri mondani, hogy az EMI császárai meztelenek. Penrose sok gondolatát átszövi a humor, ezen az egyen azonban nincs mit nevetnünk.
Martin Gardner
Mandelbrot
Mandelbrot-halmaz
fraktálok
A régi számítógépe merevlemezén őrzök egy általa letöltött tanulmányt a fraktálokról.
...
Mándy Iván egyik novellájában - úgy rémlik, de most nem tudom megtalálni - szerepel egy finom, jó illatú öreg hölgy: a neve Mandelbrot néni.
1. Lehet-e egy számítógépnek esze?
A Turing-próba
Hajlok általános elvként azt hinni, hogy az utánzat, bármilyen ügyes is, elég ügyes próbával mindig felismerhető – bár ez inkább hit (vagy tudományos optimizmus) dolga, mint bizonyított tény. Így mindent egybevéve kész vagyok a Turing-próbát saját területén nagyjából érvényesnek elfogadni. Azaz, ha a számítógép valóban képes volna minden feltett kérdést úgy megválaszolni, hogy az nem különbözne attól, ahogy egy ember válaszolna rájuk – és ezáltal alaposan3 és következetesen a bolondját járatná kérdezőnkkel – akkor ellenkező bizonyítékok hiányában az volna a sejtésem, hogy a számítógép valóban gondolkodik, érez stb. A „bizonyíték”, „valóban” és „sejtés” szavak használatához tartozik, hogy amikor a gondolkodásra, érzésre, értelemre vagy különösen a tudatosságra hivatkozom, akkor nem csupán a nyelvi hagyományoknak engedelmeskedem, hanem ezekkel a fogalmakkal objektív „dolgokat” jelölök, amelyek jelenlétét vagy hiányát fizikai testekben megpróbáljuk bizonyítani! Ezt nagyon lényeges pontnak tekintem. Amikor az ilyen tulajdonságok jelenlétét próbáljuk észrevenni, akkor a számunkra elérhető összes bizonyíték alapján teszünk sejtéseket. (Ez elvileg nem különbözik mondjuk attól, ahogy egy csillagász próbálja egy távoli csillag tömegét megállapítani.)
Miféle ellenbizonyítékokat kellene esetleg figyelembe vennünk? Erről előre nehéz szabályokat lefektetni. Világossá akarom azonban tenni, hogy azt a puszta tényt, hogy a számítógép tranzisztorokból, drótokból és hasonlókból készíthető, nem pedig neuronokból, véredényekből stb., önmagában nem tekintem ellenbizonyítéknak. Az jár a fejemben, hogy valamikor a jövőben kifejlődhet a tudatosság egy sikeres elmélete – sikeres abban az értelemben, hogy összefüggő és megfelelő fizikai elmélet, amely szépen összeillik a fizika egyéb részeivel, és amelynek jóslatai pontosan egybevágnak az emberi lények elképzeléseivel arról, hogy ők maguk mikor és milyen mértékben látszanak tudatosnak –, és hogy ez az elmélet valóban tartalmazhat állításokat számítógépünk feltételezett tudatosságáról. Még egy „tudatosságdetektort” is elképzelhetünk, amelyet ezen elmélet elvei szerint építettek, és amelyik tökéletesen megbízható az emberre nézve, de amelyik egy számítógép esetén egy Turing-próba eredményeitől eltérő eredményeket ad. Ilyen körülmények között nagyon óvatosan kellene értelmezni a Turing-próbák eredményeit. Nekem úgy tetszik, az, hogy hogyan vélekedik valaki a Turing-próba alkalmasságának kérdéséről, részben attól függ, hogyan képzeli el az illető a tudomány és technika fejlődését. E megfontolások némelyikére a későbbiekben még vissza kell majd térnünk.
Korai még, de eszembe jut Asimov R.Daneel Olivaw-ja és legfőképpen Giscardja.
Az „öröm” és a „fájdalom” egy MI-megközelítése
Mindamellett hiszem, hogy a MI komoly dolog, amelyet méltányolni kell, és amelyre figyelni kell. Nem akarom ezzel azt mondani, hogy a valódi intelligencia szimulálásában már nagyon sokra, ha egyáltalán valamire, jutottak. Nem szabad azonban elfelejtenünk, hogy a tárgykör még nagyon fiatal. A számítógépek gyorsabbak lesznek, nagyobb gyors hozzáférésű tárolóik, több logikai egységük lesz, és nagyszámú műveletet fognak párhuzamosan elvégezni. Javulás várható a logikai tervezésben és a programozási technikában is. Ezek a gépek, a MI-filozófia eszközei, technikai képességeikben hatalmasat fognak javulni. Mi több, maga a filozófia belsőleg nem abszurd. Az emberi intelligencia talán valóban nagyon pontosan utánozható lesz elektronikus számítógépekkel – lényegében a maiakkal, amelyek a már megértett elvekre alapoznak, de sokkal nagyobb kapacitásuk, sebességük stb. lesz, ami az évek során majd biztosan bekövetkezik. Ezek az eszközök talán még valóban intelligensek is lesznek; talán gondolkodni, érezni fognak, eszük lesz. Vagy talán nem, és új elvekre lesz szükség, amelyek ma még teljesen hiányoznak. Ez olyan nagy kérdés, hogy nem lehet könnyedén elutasítani. Megpróbálok bemutatni olyan bizonyítékokat, amiket a legjobbaknak látok. Végül pedig előadom saját javaslataimat..
Az EMI és Searle kínai szobája
Searle fenntartja, hogy ha az emberi agy (amelynek lehet esze) és az elektronikus számítógép (amelynek szerinte nem lehet esze) egyaránt képes lenne végrehajtani ugyanazt az algoritmust, akkor működésük között csupán anyagi felépítésükben lenne különbség. Azt állítja, de az okokat nem képes megmagyarázni, hogy a biológiai objektumoknál (agyaknál) lehet „szándékosság” és „szemantika”, amit ő a szellemi tevékenység meghatározó jellemzőinek tart, míg az elektronikusoknál nem. Számomra ez önmagában nem jelöli ki az utat az ész valamilyen hasznos, tudományos elmélete felé. Mi az olyan különleges a biológiai rendszereknél, eltekintve talán a „történelmi” módtól, ahogy fejlődtek (és attól a ténytől, hogy mi emberek történetesen ilyen rendszerek vagyunk), ami olyan objektumokká teszi azokat, hogy elérhetik a szándékosságot vagy a szemantikát? Az állítás nekem gyanúsan hasonlít egy dogmatikus kijelentésre, talán nem is kevésbé dogmatikus, mint az EMI azon állításai, amelyek szerint egy algoritmusnak puszta lejátszása elővarázsolhatja a tudatosság állapotát!
Véleményem szerint Searle-t, és nagyon sok más embert is, félrevezették a számítógépes szakemberek. Őket pedig a fizikusok. (Ez nem a fizikusok bűne. Még ők sem tudnak mindent!) Úgy látom, széles körű az a hiedelem, hogy valójában „minden digitális számítógép”. Szándékom, hogy megpróbáljak ebben a könyvben rámutatni, miért és talán hogyan nem szükségszerűen ez a helyzet.
Amennyire ki tudom bogozni, az EMI-filozófia alapját szolgáló egyik legfontosabb tényező ez az ekvivalencia a fizikai számolóeszközök között. E nézőpont szerint a hardver nem nagyon fontos (esetleg teljesen lényegtelen), a szoftver, azaz a program vagy az algoritmus az egyetlen lényeges alkotórész. Én azonban úgy látom, hogy vannak más fontos alaptényezők is, amelyek többnyire a fizika irányából jönnek. Megpróbálom vázolni, mik lehetnek ezek a tényezők.
Mi az, ami megadja egy személy egyedi azonosságát? Maguk az atomok lennének, amelyek testét alkotják? Függ-e az egyén azonossága az adott elektronoktól, protonoktól és más részecskéktől, amelyekből ezek az atomok összetevődnek? Legalább két okot lehet mondani, miért nem lehet ez így. Elsősorban, bármelyik élő személy testének anyaga állandóan cserélődik. Ez különösen áll az agy sejtjeire, annak ellenére, hogy a születés után új agysejtek többé nem keletkeznek. Minden élő sejtben (az agysejteket is beleértve) az atomok hatalmas többsége – tulajdonképpen testünk teljes anyaga – a születés után sokszor kicserélődik.
A második ok a kvantumfizikából jön – és különös irónia, hogy szigorúan véve ellentmondásban áll az elsővel! A kvantummechanika szerint (erről többet majd a 6. fejezetben fogunk látni) bármely két elektron szükségszerűen tökéletesen azonos kell legyen, és ugyanez érvényes bármely két protonra és bármely két, azonos típusú részecskére. Nem csak arról van szó, hogy nincs mód a részecskék megkülönböztetésére, az állítás ennél lényegesen erősebb. Ha egy ember agyának egy elektronját kicserélnék egy tégla egy elektronjával, akkor a rendszer állapota pontosan14 ugyanaz az állapot lenne, mint előtte, nem csupán attól megkülönböztethetetlen! Ugyanez érvényes a protonokra és bármilyen fajta részecskékre, egész atomokra, molekulákra stb. Ha egy ember teljes anyagi tartalmát kicserélnék a házának tégláiban lévő megfelelő részecskékkel, akkor szigorú értelemben az égvilágon semmi sem történne. Az embert a házától az a minta különbözteti meg, ahogyan alkotórészei elrendeződnek, nem pedig maguknak az alkotórészeknek az egyénisége.
Hardver és szoftver
Ezzel kapcsolatos egy gyakran tárgyalt ötlet, a tudományos-fantasztikus irodalom távfuvarozó gépe.15 Az elképzelés szerint ez a „szállítás” egyfajta módja, mondjuk egyik bolygóról egy másikra, de hogy valójában lehetséges-e, erről vita folyik. Ahelyett, hogy egy űrhajó a „rendes” módon fizikailag szállítaná, a leendő utazót tetőtől talpig letapogatják, és a legteljesebb részletességgel feljegyzik a testében lévő minden atom és minden elektron pontos helyzetét és teljes leírását. Mindezt az információt elektromágneses jellel (fénysebességgel) átsugározzák a rendeltetési helyre, a távoli bolygóra. Ott az információt összegyűjtik, és arra használják, hogy segítségével összeállítsák az utazó pontos másolatát, egész memóriájával, szándékaival, reményeivel és legmélyebb érzéseivel együtt. Ennyit mindenképpen elvárnak, minthogy az agy állapotának minden részletét hűen feljegyezték, átküldték és rekonstruálták. Feltételezve, hogy a mechanizmus működik, az utazó eredeti példánya „nyugodtan” megsemmisíthető. A kérdés természetesen az: valóban utazási módszer-e ez egyik helyről a másikra, vagy csupán egy másolat készítése és az eredeti meggyilkolása? Kész volna-e Ön használni az „utazásnak” ezt a módját – feltéve, hogy kimutatták róla, hogy saját keretein belül teljesen megbízható? Ha a távfuvarozás nem utazás, akkor milyen elvi különbség mutatkozik közte és aközött, ha csak szépen átsétálunk egyik szobából a másikba? Az utóbbi esetben nem arról van-e szó, hogy valakinek az atomjai az egyik pillanatban megadják az atomok következő pillanatbeli helyére vonatkozó információt? Végül is láttuk, hogy az egyes atomok azonossága megőrzésének nincs jelentősége, sőt még értelmetlen is az egyes atomok azonosságáról beszélni. Nem képez-e az atomoknak minden mozgó alakzata egyfajta információs hullámot, amely átterjed egyik helyről a másikra? Hol van a lényeges különbség a hullámok terjedése között, aminek segítségével a szokásos módon lehet leírni utazónk átballagását egyik szobából a másikba, és aközött, ami a távfuvarozó műszerben végbemegy?
Van-e bármi olyan a fizika törvényeiben, ami elvileg lehetetlenné teszi a távfuvarozást? Másrészt esetleg az a helyzet, hogy elvileg semmi nem szól egy személynek és egy személy tudatának ilyen átvitele ellen, de a „másoló” folyamat szükségszerűen megsemmisítené az eredetit? Lehet, hogy a két életképes példány megőrzése az, ami elvileg lehetetlen? Úgy vélem, hogy bármily szokatlanok is e gondolatok, talán van valami jelentőségük, ki lehet hámozni belőlük valamit a tudat és egyéniség fizikai természetére vonatkozóan. Azt hiszem, támpontot nyújtanak, jelzik a kvantummechanika fontos szerepét a tudati jelenségek megértésében. De ne siessünk előre! Vissza kell majd térnünk ezekre a dolgokra, miután megvizsgáltuk a kvantumelmélet szerkezetét a 6. fejezetben.
Egyelőre azonban fogadjuk el azt a (mindennapos) nézetet, hogy minden lényeges fizikát lehet digitális számításokkal modellezni. Ekkor a „műveleti” az egyetlen reális feltevés (az időre és a számítások terjedelmére vonatkozó kérdésektől eltekintve), azaz hogy ha valami teljesen hasonlóan cselekszik, mint egy tudatos dolog, akkor el kell fogadnunk, hogy magát annak a dolognak is „érzi”.
Az EMI-szemlélet azt tartja, hogy „csupán” hardverkérdés lévén, minden, az agy munkája során ténylegesen előhívott fizika szükségszerűen szimulálható kell legyen megfelelő átalakító szoftver bevezetésével. Ha elfogadjuk a műveleti nézőpontot, akkor a kérdés az univerzális Turing-gépek ekvivalenciáján és azon a tényen alapszik, hogy egy ilyen géppel valóban minden algoritmus végrehajtható – együtt a feltevéssel, hogy az agy tényleg valamilyen algoritmus szerint működik.
2. Algoritmusok és Turing-gépek
Az algoritmusfogalom háttere
Mi pontosan egy algoritmus vagy egy Turing-gép, vagy egy univerzális Turing-gép? Miért annyira alapvetőek e fogalmak annak modern megítélésében, hogy mi képezhet „gondolkodó eszközt”? Vannak-e abszolút korlátai annak, mit érhet el elvileg egy algoritmus? Hogy ezeket a kérdéseket megfelelő formában tudjuk felvetni, meg kell vizsgálnunk az algoritmus és a Turing-gépek fogalmát kicsit részletesebben.
Az „algoritmus” szó a kilencedik századbeli perzsa matematikus, Abu Dzsáfár Mohammed ibn Músza al-Hvárizmi nevéből származik, aki i. sz. 825 körül nagy hatású matematikai tankönyvet írt „Kitab al jabr w’al-muqabala” címmel. Az „algoritmus” ma használatos, a korábbi és pontosabb „algorizmus”-tól eltérő alakja valószínűleg az „aritmetika” szóhoz való társítás következménye. (Érdemes megjegyezni, hogy az „algebra” szó az említett könyv címében előforduló arab „al jabr” szóból származik.)"
"Algoritmusokra példákat azonban al-Hvárizmi könyvénél már sokkal korábban ismertek. Az egyik legnépszerűbb az ókori görög időkből (kb. i. e. 300-ból) származó, ma euklideszi algoritmus néven ismert eljárás, két szám legnagyobb közös osztójának meghatározására.
Eukleidész algoritmusa csak egy a számos, gyakran nagyon régóta ismert, algoritmikus eljárás közül, amelyek a matematika minden területén megtalálhatóak. Figyelemre méltó azonban, hogy algoritmusok speciális példáinak ókori történeti eredete ellenére az általános algoritmusfogalom pontos megalkotása csak ebben a században történt meg. Valójában e fogalom változatos alternatív leírásait adták meg, mindet az 1930-as években. Ezek közül a legközvetlenebb, a leginkább meggyőző és történetileg is a legfontosabb az, amelyik a Turing-gép néven ismert fogalmat használja.
...
Amit egy Turing-„gépről” tudnunk kell, hogy az egy darab „absztrakt matematika”, és nem fizikai objektum. A fogalmat az angol matematikus, kódfejtő szakértő és úttörő számítógéptudós, Alan Turing vezette be 1935–36-ban (Turing 1937), hogy segítségével megbirkózzon egy nagyon széles körű, az eldönthetőségi probléma (Entscheidungsproblem) néven ismert kérdéssel, amelyet a nagy német matematikus, David Hilbert vetett fel.
Absztrakt, elvont, nem anyagi létező. Platon világa.
...
Hilbert nem kevesebbet keresett, mint egy általános algoritmikus eljárást a matematikai problémák megoldására, vagy inkább választ arra a kérdésre, hogy ilyen eljárás elvileg létezhet-e vagy sem. "
"Hilbertnek volt olyan programja is, hogy a matematikát egyszer s mindenkorra lefektetett axiómákkal és eljárási szabályokkal megtámadhatatlan, tökéletes alapra helyezze, de mire Turing nagy munkájával előállt, addigra erre a programra már megsemmisítő csapást mért egy meglepő tétel, amelyet 1931-ben bizonyított be a briliáns osztrák logista, Kurt Gödel.
...
"Hilbertnek az a problémája, amellyel Turing foglalkozott (az eldönthetőségi probléma), túlment a matematika minden speciális, axiomatikus rendszerek formájában való megfogalmazásán. A kérdés a következő volt: van-e általános, mechanikus eljárás, amellyel elvileg megoldható lenne a matematika minden (alkalmasan meghatározott osztályba tartozó) problémája, egyik a másik után?"
...
"A kérdés megválaszolásának nehézsége részben annak eldöntése volt, mit értsünk „mechanikus eljárás” alatt. E fogalom kívül esett az akkori idők rendes matematikai elképzelésein. Hogy ezzel megmérkőzzön, Turing megpróbálta elképzelni, hogyan lehetne a „gép” fogalmát formálissá tenni, működését elemi egységekre bontani. Világosan látszik, hogy Turing saját értelmezésében az emberi agyat is a „gépek” egyikének tekintette, úgyhogy bármilyen tevékenységet hajtsanak is végre a matematikával foglalkozó emberek, amikor matematikai problémáikkal birkóznak, ezekre is a „mechanikus eljárás” címkéjét ragasztotta volna."
...
"Turing ténylegesen megmutatta, hogy vannak olyan tökéletesen jól meghatározott matematikai műveletek, amelyeket semmilyen közönséges értelemben nem lehet mechanikusnak nevezni! Van talán némi irónia abban, hogy éppen Turing munkájának ez az oldala jelenthet közvetett módon egérutat számunkra, amelyen kiléphetünk a szellemi jelenségek természetének Turing-féle koncepciójából."
Turing koncepciója
"Próbáljunk elképzelni egy gépet, amely valamilyen (végesen definiálható) számítási eljárást hajt végre. Milyen lenne ennek általános alakja? Fel kell készülnünk arra, hogy egy kicsit idealizáljunk, és ne törődjünk túl sokat a gyakorlati dolgokkal: valójában egy matematikailag idealizált „gépről” gondolkodunk. Gépünktől azt várjuk, hogy különböző lehetséges állapotai egy diszkrét sorozatot alkossanak, számuk véges (bár esetleg nagyon nagy szám) legyen. Ezeket a gép belső állapotainak nevezzük. Nem akarjuk azonban korlátozni a számítások méretét, amelyeket gépünk elvileg végre fog hajtani. "
...
"Így bár gépünknek véges számú belső állapota van, tudnia kell kezelni olyan adatbevitelt is, amely méretében nem korlátozott. "
...
"Mivel gépünknek csak véges számú különböző belső állapota van, nem lehet tőle elvárni azt, hogy az összes külső adatot vagy számításainak összes eredményét „magában hordozza”. Ehelyett az adatoknak vagy az előző számításoknak csak azokat a részeit kell vizsgálnia, amelyekkel közvetlenül foglalkozik, ezeken kell elvégeznie a szükséges műveletet."
...
"Lejegyezheti, esetleg a külső tárolóterületen a művelet lényeges eredményeit, azután pontosan meghatározott módon áttérhet feladatának következő szakaszára. A korlátlan bevitel, számítási terület és kivitel az, ami elárulja, hogy csak egy matematikai idealizációról beszélünk, és nem valami olyanról, amit a gyakorlatban valóban meg lehetne valósítani "
...
"akármilyen szemmel nézünk is rá, Turing idealizációját valóban figyelemreméltóan jól megközelítik a mai elektronikus számítógépek."
...
"az eszköz minden bevitelét környezetéből kapja. Úgy használja a környezetet, mint saját „durva papírját”. Kivitelét végül ugyanebbe a környezetbe írja ki.
Turing leírásában a „szalag” négyzeteknek egy lineáris sorozatából áll, amely mindkét irányban végtelen. A szalagon minden négyzet vagy üres, vagy egyetlen jelet tartalmaz.17 A megjelölt és jelöletlen négyzetek használata azt mutatja, hogy megengedjük „környezetünk” (azaz a szalag) lebontását, és (a folytonossal szemben) diszkrét elemekkel való leírását. Ez ésszerűnek látszik, ha azt kívánjuk, hogy eszközünk megbízható és abszolút meghatározott módon működjék. Megengedjük azonban, hogy ez a „környezet” (potenciálisan) végtelen legyen, ami az általunk használt matematikai idealizáció sajátossága, de a bevitel, a számítás és a kivitel bármelyik speciális esetben mindig véges kell maradjon. Így bár a szalagot végtelen hosszúnak vesszük, csak véges számú jel lehet rajta. Egy bizonyos ponton túl mindkét irányban teljesen üresnek kell lennie."
...
"Annak teljes magyarázata, miért csinálja meg az EUC (vagy az UN×2) azt, amit elvárunk tőle, tartalmaz bizonyos finomságokat, és sokkal bonyolultabb lenne elmondani, mint amennyire bonyolult a gép maga – nem szokatlan tulajdonsága ez a számítógépprogramoknak! (Hogy miért csinálja egy algoritmikus eljárás meg azt, amit feltételeznek róla, ennek teljes megértéséhez meglátások kellenek. Algoritmikusak-e maguk a „meglátások”? Ez olyan kérdés, amely a későbbiekben fontos lesz számunkra.)"
A numerikus adatok kettes rendszerbeli kódolása
...
"A fentiek adnak némi elképzelést arról, mire képesek a Turing-gépek nagyon elemi szinten. Ahogy az várható, ezek a gépek roppant bonyolulttá válhatnak és ténylegesen azzá is válnak, ha némileg összetett műveleteket kell végrehajtaniuk. Mi tehát végül az ilyen eszközök működési területe? Ezt a kérdést vizsgáljuk a következőkben."
A Church-Turing tétel
..."Még továbbmenve, olyan Turing-gépeket is lehet készíteni, amelyeknél nincs előre rögzítve, milyen aritmetikai műveletet kell végrehajtani, de az erre szolgáló utasítások rajta vannak a szalagon. Lehet, hogy valamelyik lépésben az éppen elvégzendő művelet függ valamelyik olyan számítás eredményétől, amelyet a gépnek egy korábbi szakaszban kellett elvégeznie. („Ha ennek a számításnak az eredménye nagyobb, mint ez és ez, akkor csináld ezt; egyébként csináld azt.”) Ha egyszer meggyőződtünk arról, hogy lehet olyan Turing-gépeket csinálni, amelyek aritmetikai vagy egyszerű logikai műveleteket végrehajtanak, akkor könnyebben el tudjuk képzelni, hogyan lehet velük bonyolultabb, algoritmikus természetű feladatokat elvégeztetni. Ha az ember játszott már ilyen dolgokkal, akkor könnyen megnyugszik abban, hogy egy effajta géppel bármilyen mechanikus műveletet el lehet végeztetni! Ésszerűnek látszik matematikailag úgy definiálni egy mechanikus műveletet, mint amit egy ilyen gép végre tud hajtani. Az „algoritmus” főnevet és a „kiszámítható”, „rekurzív” és „végrehajtható” mellékneveket a matematikusok mind az olyan mechanikus műveletek megjelölésére használják, amelyeket ilyen típusú elméleti gépekkel – a Turing-gépekkel – végre lehet hajtani. Amennyiben egy eljárás elég világos és mechanikus, akkor joggal gondolhatjuk, hogy valóban lehet találni olyan Turing-gépet, amely végrehajtja azt. "
"Másrészről esetleg még úgy érezhető, hogy az ilyen gépek tervezését talán szükségtelenül korlátoztuk. Első pillantásra ilyen korlátozásnak tűnik az, hogy az eszköz egyszerre csak egy bináris jegyet (0-t vagy 1-t) olvashat el, és hogy egyszerre csak egy lépésnyit mozdulhat el, és csak egyetlen egydimenziós szalag mentén."
"Láthatjuk, hogy amíg a Turing-gép talál üres helyet az adott szalagon, addig nincs szükség egynél több szalagra. Ehhez viszont szükség lehet arra, hogy a szalagon az adatokat áthelyezze egyik helyről a másikra. Lehet, hogy ez „rossz hatásfokú”, de nem korlátozza azt, ami elvileg elérhető.20 Hasonlóképpen, elvileg nem nyerünk semmit több Turing-gép párhuzamos működtetésével (ami az utóbbi évek divatossá vált elképzelése az emberi agy jobb modellezésének szándékától hajtva), bár bizonyos körülmények között a működési sebesség megnövekedhet. Két, egymással közvetlenül nem kommunikáló, különálló géppel nem lehet többet elérni, mint két egymással kommunikálóval, ha pedig kapcsolat van közöttük, akkor valójában egyetlen gépnek számítanak!"
"Mi a helyzet Turingnak azzal a megszorításával, hogy a szalag egydimenziós? Ha úgy gondolunk a szalagra, hogy az a „környezetet” képviseli, akkor lehet, hogy jobban szeretnénk, ha nem egydimenziós lenne, hanem egy sík felület, esetleg háromdimenziós szerkezet. Egy sík felület látszólag közelebb állhat ahhoz, ami egy „folyamattáblához” szükséges (például az euklideszi algoritmus működésének előbbi leírásában).21 Elvi nehézség azonban nincs abban, hogy egy folyamatábra működését „egydimenziós” formában (például a táblázat közönséges szóbeli leírásával) adjuk meg. A kétdimenziós síkbeli megjelenítés csak saját kényelmünket és a könnyebb érthetőséget szolgálja, és nem befolyásolja azt, hogy elvileg mit lehet elérni. Egy jel vagy objektum helyzetét a kétdimenziós síkon, sőt a háromdimenziós térben is mindig világos módon fel lehet jegyezni egydimenziós szalagra. (Egy kétdimenziós sík használata valójában tökéletesen ekvivalens két szalag használatával. A két szalag szolgáltatná a két „koordinátát”, amelyre szükség van a kétdimenziós sík egy pontjának megadásához; hasonlóképpen három szalag elő tudja állítani a háromdimenziós tér egy pontjának koordinátáit.) Ez az egydimenziós kódolás megint „rossz hatásfokú” lehet, de ez nem befolyásolja azt, hogy mit lehet elvileg elérni."
Vonal.Sík.Tér
"Ez jelentősen megerősítette azt a nézőpontot, amely a Church–Turing-tétel néven vált ismertté, hogy a Turing-gép (vagy az azzal ekvivalens) fogalom valójában definiálja azt, amit matematikailag algoritmikus (végrehajtható, rekurzív, mechanikus) eljárás alatt értünk. ...
ma:
"arra irányul a figyelem, hogy vajon a valódi fizikai rendszerek (ideértve feltehetően az emberi agyat is) – amelyek pontos fizikai törvények szerint működnek –, többet, kevesebbet vagy pontosan ugyanazokat a logikai és matematikai műveleteket képesek-e végrehajtani, mint a Turing-gépek. Én nagyon boldogan elfogadom a Church–Turing-tétel eredeti matematikai alakját. A valóságos fizikai rendszerek viselkedésével való kapcsolata viszont külön probléma, amely könyvünkben később az egyik fő kérdés lesz.
Számok, amelyek nem természetes számok
"Az előző vizsgálatban természetes számokkal végzett műveleteket néztünk, és megjegyeztük azt a figyelemre méltó tényt, hogy egy önmagában álló Turing-gép tetszőlegesen nagy természetes számokat képes kezelni annak ellenére, hogy minden gépnek meghatározott, véges számú, különböző belső állapota van."
"Gyakran kell azonban bonyolultabb számokkal dolgozni, negatív számokkal, törtekkel vagy végtelen tizedes törtekkel."
"A negatív számok és a törtek (például az olyan számok, mint a –597/26) könnyen kezelhetők Turing-gépekkel, és a számlálók és nevezők akármilyen nagyok lehetnek."
"A negatív számok és a törtek így természetes számok véges sorozataival kezelhetőek, ezért a kiszámíthatóság általános kérdését illetően semmi újat nem hoznak.
"Hasonlóképpen nem adnak semmi újat a tetszőleges hosszúságú véges tizedes törtek sem, mivel ezek csupán a törtek speciális esetei. "
"A valóságban bizonyára létezik olyan Turing-gép, amely ebben az értelemben kiadja a π teljes tizedes tört kifejtését, bár egy kissé bonyolult volna explicit módon kidolgozni azt. Hasonló megjegyzés érvényes sok más irracionális számra, mint például a
search = 1, 414213562…-re. A helyzet azonban az, hogy egyes irracionális számok (figyelemre méltóan) egyáltalán nem állíthatók elő semmiféle Turing-géppel, amint azt a következő fejezetben látni fogjuk. Azokat a számokat, amelyeket elő lehet ilyen módon állítani, kiszámíthatóaknak nevezik (Turing 1937). Amelyeket nem lehet (a hatalmas többség ilyen!), azok a nem kiszámíthatóak."
"Erre és rokon problémákra a későbbi fejezetekben vissza fogok térni. Lesz bizonyos jelentősége számunkra azzal a kérdéssel kapcsolatban, hogy vajon egy valóságos fizikai objektum (például az emberi agy) fizikai elméleteink szerint megfelelően leírható-e kiszámítható matematikai szerkezetekkel kifejezve.
A kiszámíthatóság kérdése a matematikában általánosságban fontos. Nem úgy kell gondolni rá, mint ami csak számokra mint olyanokra vonatkozik. Lehetnek olyan Turing-gépek, amelyek közvetlenül matematikai képletekkel, például algebrai vagy trigonometrikus kifejezésekkel dolgoznak, vagy amelyek a kalkulus formális manipulációit csinálják végig. "
"Nincs másra szükség, mint az összes előforduló matematikai szimbólum 0-kból és 1-ekből álló sorozatokba való pontos kódolásának valamilyen formájára, és ekkor a Turing-gép fogalma alkalmazható. Végül is ez járhatott Turing fejében, amikor nekilátott az eldönthetőségi probléma megoldásához, amely algoritmikus eljárást keres általános természetű matematikai kérdések megválaszolására."
Az univerzális Turing-gép
Nem írtam még le az univerzális Turing-gép fogalmát. Az elvet nem túl nehéz megadni, bár a részletek bonyolultak. Az alapeszme az, hogy egy tetszőleges T Turing-gép utasításainak listáját egy 0-kból és 1-kből álló füzérbe kódoljuk át, ezt szalagon lehet ábrázolni. Ezt a szalagot használjuk azután valamilyen speciális U Turing-gép bevitele kezdeti részének – U-t nevezzük majd univerzális Turing-gépnek. A bevitel maradék részére U éppen úgy hat, mint ahogy T tenné. Az univerzális Turing-gép egy univerzális utánzó. A szalag kezdeti része megadja az U univerzális gépnek a teljes információt, amire annak szüksége van, hogy pontosan utánozzon bármilyen adott T gépet!
Működésének megértéséhez először szükségünk van a Turing-gépek szisztematikus megszámozására."
....
"
A Hilbert-féle probléma megoldhatatlansága
Térjünk most rá arra, amiért Turing elképzeléseit eredetileg felvetette, hogy megadja a választ Hilbert nagyon általános eldönthetőségi problémájára: létezik-e mechanikus eljárás valamilyen széles, de jól meghatározott osztályba tartozó matematikai problémák megoldására? Turing rájött, hogy a kérdést át tudja fogalmazni annak a problémának eldöntésére, hogy megáll-e vagy sem valamikor az n-edik Turing-gép, amikor az m számra hat. Erre a problémára mint megállási problémára hivatkoztak. "
...
"A matematika számára fontos lenne, hogy képesek legyünk eldönteni, mikor állnak le a Turing-gépek. Tekintsük például a következő egyenletet:
(x + 1)w + 3 + (y + 1)w + 3 = (z + 1)w + 3.
(Ha Ön a matematikai egyenleteket nem igazán kedveli, ez még ne szegje kedvét! Ezt most csak példaként mutatom, nincs szükség arra, hogy a részleteket is értse.) Ez a speciális egyenlet a matematika egyik híres megoldatlan problémájához kapcsolódik – talán mind közül a leghíresebbhez. A probléma a következő: vannak-e olyan w, x, y, z természetes számok, amelyekre a fenti egyenlet teljesül? A „Fermat utolsó tétele” (nagy Fermat-tétel) néven ismert híres állítás, amelyet a tizenhetedik századbeli kiváló francia matematikus, Pierre de Fermat (1601–1665) Diofantosz Arithmeticájának margójára írt, azt mondja, hogy az egyenlet soha nem teljesül.25 Bár foglalkozására nézve jogász (és Descartes kortársa), Fermat korának legkitűnőbb matematikusa volt. Azt állította, hogy tételére „igazán csodálatos bizonyítása” van, de a margó túl kicsi volt, így nem fért rá; azonban mind a mai napig senki nem volt képes rekonstruálni egy ilyen bizonyítást, viszont ellenpéldát sem tudtak a nagy Fermat-tételre találni!
Világos, hogy ha adott a (w, x, y, z) számnégyes, akkor csupán számolás kérdése annak eldöntése, hogy az egyenlőség fennáll-e vagy sem. Ezért el tudunk képzelni olyan számítógép-algoritmust, amely végigfut egymás után minden számnégyesen, és csak akkor áll meg, ha az egyenlet teljesül. (Láttuk, hogy vannak módok véges számsorozatok kiszámítható kódolására egyetlen szalagon, azaz egyetlen számként, így „végigfuthatunk” minden számnégyesen, követve ezen egyetlen számok természetes sorrendjét.) Ha meg tudnánk állapítani, hogy ez az algoritmus nem áll meg, akkor bizonyításunk lenne Fermat tételére."
...
Egy csodálatos elme- azt hiszem az volt a címe.
...
"Felvetődik egy természetes kérdés: hogyan döntsük el, hogy bármelyik speciális Turing-gép (meghatározott bemeneti adatokat betáplálva) megáll-e valamikor? Sok Turing-gépre ezt nem lehet nehéz megválaszolni; de a válasz, mint előbb láttuk, olykor egy komoly matematikai probléma megoldását foglalja magában. Van-e tehát valamilyen algoritmikus eljárás az általános kérdés – a megállási probléma – teljesen automatikus megválaszolására? Turing megmutatta, hogy nincs."
..."Az a kérdés, hogy egy Turing-gép megáll-e vagy sem, a matematikának egy tökéletesen jól meghatározott darabja (és már láttuk, hogy megfordítva: változatos, jelentős matematikai kérdések fogalmazhatók meg Turing-gépek megállásának problémájaként). Így megmutatva, hogy nem létezik algoritmus annak a kérdésnek eldöntésére, hogy megállnak-e a Turing-gépek, Turing bebizonyította (és ezt tette Church is saját, meglehetősen különböző megközelítésében), hogy a matematikai kérdések eldöntésére nem létezhet általános algoritmus. Hilbert eldönthetőségi problémájának nincs megoldása! "
..."Úgy tűnhet, most azt állapítottuk meg, hogy van legalább néhány eldönthetetlen matematikai kérdés. Azonban semmi ilyet nem csináltunk. Nem azt mutattuk meg, hogy van valamilyen különösen szörnyűséges Turing-gép táblázat, amelynél, valamiféle abszolút értelemben, lehetetlen eldönteni, megáll-e a gép vagy sem, amikor valamilyen különösen szörnyű számot táplálunk belé – a helyzet valójában éppen az ellenkező, amint azt egy pillanaton belül látni fogjuk. Nem mondtunk semmit egyes problémák megoldhatatlanságáról, csak problémák egyes családjainak algoritmikus megoldhatatlanságáról. A válasz bármelyik egyedi esetben vagy „igen”, vagy „nem”, így az adott eset eldöntésére bizonyára van algoritmus, nevezetesen az, amely egyszerűen „igen”-t mond, amikor feladjuk neki a problémát, vagy amelyik egyszerűen „nem”-et mond, ami szintén előfordulhat! A nehézség természetesen az, hogy nem tudhatjuk, melyik algoritmust használjuk. Ez egyetlen állítás matematikai igazsága kiderítésének, nem pedig állítások egy családja szisztematikus eldöntésének kérdése. Fontos felismerni azt, hogy az algoritmusok magukban nem döntik el a matematikai igazságot. Egy algoritmus érvényességét mindig külső eszközökkel kell megállapítani.
Hogyan győzzünk le egy algoritmust?
A matematikai állítások igazsága eldöntésének kérdésére később, Gödel tételével kapcsolatban visszatérünk (lásd a 4. fejezetet). Most rá szeretnék mutatni arra, hogy Turing érvelése valójában sokkal építőbb és kevésbé negatív, mint amilyennek eddig látszólag bemutattam. Nem mutattunk még olyan speciális Turing-gépet, amelynél, valamilyen abszolút értelemben, eldönthetetlen, hogy megáll-e vagy sem. Ha azonban gondosan megvizsgáljuk az érvelést, akkor azt találjuk, hogy eljárásunk maga hallgatólagosan már megadja a választ a látszólag „különösen szörnyűséges” gépeket illetően. Most Turing eljárását használva fogunk egy ilyet készíteni!
Church lambda-kalkulusa


A kiszámíthatóság fogalma nagyon fontos és szép matematikai elképzelés. Figyelemre méltóan új is – ahhoz képest, ahogy az ilyen alapvető dolgok mennek a matematikában –, hiszen először az 1930-as években vetették fel. Olyan elképzelés, amely végigvonul a matematika minden területén (jóllehet a legtöbb matematikus egyelőre nem nagyon izgatja magát a kiszámíthatósági kérdésekkel). Ereje részben abból a tényből táplálkozik, hogy a matematikában egyes jól meghatározott műveletek valójában nem kiszámíthatóak (ilyen egy Turing-gép megállásának eldöntése; a 4. fejezetben látunk majd egyéb példákat is). Ha ilyen nem kiszámítható dolgok nem lennének, akkor a kiszámíthatóság fogalmának nem lenne sok matematikai érdekessége. A matematikusok szeretik a rejtvényeket. Számukra érdekes rejtvény lehet annak eldöntése, hogy valamilyen matematikai művelet kiszámítható-e vagy sem. És különösen érdekes azért, mivel ennek a rejtvénynek az általános megoldása maga nem kiszámítható!
λx.[fx],
akkor ezen azt a függvényt értjük, amely mondjuk a-ra hatva az fa eredményt adja. Azaz
(λx.[fx])a = fa.
Más szavakkal λx.[fx] egyszerűen az f függvény, azaz
λx.[fx] = f.
Érdemes egy kicsit elgondolkodni. Egyike ez azoknak a matematikai szépségeknek, amelyek első ránézésre olyan szőrszálhasogatóak és maguktól értetődőek, hogy hajlamosak vagyunk a lényeget teljesen elveszteni. Vegyünk egy példát a jól ismert iskolai matematikából! Legyen az f függvény egy trigonometriai művelet, egy szög szinusza, ekkor a „sin” absztrakt függvény definíciója a következő: λx.[sin x] = sin."
Ideák.
Talán megtalálom azokat a részeket egy - amúgy általam kedvelt - blogon, ahol eléggé egyedül maradva, kilátástalanul védtem Domokos Gábort, a Gömböc szülő atyját, nemtelen komment-támadásokkal szemben, melyeket
azzal indokoltak a támadók, hogy micsoda tudománytalan dolog az, hogy Domokos saját sejtései igazolására Platon kockáit hozza fel egy komoly tudományos folyóiratban közölt cikkében.
...
"Végül 1937-ben Church és Turing egymástól függetlenül megmutatták, hogy minden kiszámítható (vagy algoritmikus) művelet – most Turing-gépek értelmében – megadható valamilyen Church-kifejezéssel (és fordítva).
...
3. Matematika és valóság...
Tor’Bled-Nam országa



Képzeljük el, hogy nagy útra indultunk egy távoli világba. Ezt a világot Tor’Bled-Namnak fogjuk hívni. Távoli detektorunk elcsípett egy jelet, amely most jelent meg az előttünk lévő képernyőn. A kép fókuszálása után ezt látjuk (3.1. ábra):
...

"Mi lehet ez a különös, változatos és csodálatosan bonyolult világ, amely utunkba került? Bizonyára sok Olvasó ismeri már, egyesek viszont még nem találkoztak vele. Ez a világ nem más, mint egy darab absztrakt matematika – a Mandelbrot nevét viselő halmaz.31 Kétségkívül nagyon bonyolult; mégis figyelemre méltóan egyszerű szabállyal képezhető! Hogy a szabályt rendesen el tudjam mondani, először azt kell elmagyaráznom, mi is egy komplex szám. Most tehát ez következik. A komplex számokra később szükségünk lesz. Abszolút alapvetőek a kvantummechanika szerkezetében, és ezért világunk működésében is, amelyben élünk. A Matematika Nagy Csodái közül is ezek alkotják az egyiket. Hogy elmagyarázzam, mi egy komplex szám, először arra kell emlékeztetnem az Olvasót, mit értünk a „valós szám” kifejezésen. Segíteni fog az is, ha utalunk e fogalom és a „való világ” realitásának kapcsolatára!"
..."Nagyon sok olyan valós szám is van azonban, amely ebben az értelemben nem kiszámítható. Az előző fejezetben láttuk, hogy vannak nem kiszámítható sorozatok, amelyek mindazonáltal tökéletesen jól meghatározottak. Vehetnénk például azt a tizedes kifejtést, amelynek π-edik jegye aszerint 0 vagy 1, hogy az n-edik Turing-gép az n számra hatva megáll-e vagy sem. A valós számoktól általában csak azt várjuk el, hogy legyen valamilyen végtelen tizedes kifejtésük. Nem várjuk, hogy legyen algoritmus az n-edik jegy előállítására, sőt még azt sem, hogy legyen tudomásunk bármilyen szabályról, amely elvileg meghatározza, hogy mi az n-edik jegy.33 A kiszámítható számokkal szörnyű dolgozni. Nem tudjuk megőrizni minden művelet kiszámíthatóságát még akkor sem, ha csak kiszámítható számokkal dolgozunk. Például még az sem kiszámítható, hogy két tetszőleges, kiszámítható számról eldöntsük, egyenlőek-e vagy sem! Ezért inkább dolgozunk az összes valós számmal, amikor a tizedes kifejtés bármilyen lehet, nem kell, hogy mondjuk egy kiszámítható sorozat legyen...
..."Nagyon sok olyan valós szám is van azonban, amely ebben az értelemben nem kiszámítható. Az előző fejezetben láttuk, hogy vannak nem kiszámítható sorozatok, amelyek mindazonáltal tökéletesen jól meghatározottak. Vehetnénk például azt a tizedes kifejtést, amelynek π-edik jegye aszerint 0 vagy 1, hogy az n-edik Turing-gép az n számra hatva megáll-e vagy sem. A valós számoktól általában csak azt várjuk el, hogy legyen valamilyen végtelen tizedes kifejtésük. Nem várjuk, hogy legyen algoritmus az n-edik jegy előállítására, sőt még azt sem, hogy legyen tudomásunk bármilyen szabályról, amely elvileg meghatározza, hogy mi az n-edik jegy.33 A kiszámítható számokkal szörnyű dolgozni. Nem tudjuk megőrizni minden művelet kiszámíthatóságát még akkor sem, ha csak kiszámítható számokkal dolgozunk. Például még az sem kiszámítható, hogy két tetszőleges, kiszámítható számról eldöntsük, egyenlőek-e vagy sem! Ezért inkább dolgozunk az összes valós számmal, amikor a tizedes kifejtés bármilyen lehet, nem kell, hogy mondjuk egy kiszámítható sorozat legyen...
Hány valós szám van?
Tartsunk egy kis szünetet, hogy méltányolhassuk az általánosítás nagyságát, melynek során a racionális számoktól eljutottunk a valósakig.
Elsőre azt gondolhatnánk, hogy már az egészek száma is nagyobb a természetes számokénál, mert minden természetes szám egész, míg egyes egészek (a negatívak) nem természetes számok; hasonlóképpen azt is gondolhatnánk, hogy a törtek száma nagyobb, mint az egészeké. Azonban ez nem így van. A végtelen számok szép és hatékony elmélete szerint, amelyet az igen eredeti orosz-német matematikus, Georg Cantor tett közzé az 1800-as évek végén, a törtek, az egészek és a természetes számok teljes száma ugyanaz az ℵ0-lal („alef null”) jelölt végtelen szám. (Érdemes megjegyezni, hogy már 250 évvel korábban, a korai 1600-as években voltak hasonló elképzelései a nagy itáliai fizikusnak és csillagásznak, Galileo Galileinek. Néhány más eredményét az 5. fejezetben felidézzük.) Hogy az egészek száma ugyanannyi, mint a természetes számoké, azt a következő „egy-egy értelmű megfeleltetésből” láthatjuk:" ...
...
.."Vegyük észre, hogy minden egész szám (a bal oldali oszlopban) és minden természetes szám (a jobb oldaliban) egyszer és csak egyszer fordul elő a táblázatban. Ez vagy az ehhez hasonló egy-egy megfeleltetés alapozza meg a Cantor-elméletben azt, hogy a bal és jobb oldali oszlopokban lévő elemek száma ugyanannyi. Az egészek száma így valóban azonos a természetes számokéval. A szám ebben az esetben végtelen, de ez nem számít. (Az egyetlen különlegesség, amely végtelen számokkal előfordul, az, hogy az egyik lista egyes tagjait elhagyhatjuk, és még így is találunk egy-egy megfeleltetést a két lista között!) Hasonló, de valamivel bonyolultabb módon egy-egy megfeleltetést állíthatunk fel a törtek és az egészek között. (Felhasználhatjuk ehhez a természetes számpárok, a számlálók és nevezők egyetlen természetes számmal való ábrázolásának egyik módját; lásd a 2. fejezetet.) A természetes számokkal egy-egy megfeleltetésbe hozható halmazokat megszámlálhatóaknak nevezzük, így a megszámlálhatóan végtelen halmazoknak van ℵ0 elemük. Most láttuk, hogy az egészek megszámlálhatóak, és ilyenek az összes törtek is."...
"Átlós eljárásunk ad tehát egy valós számot, de ez nem kiszámítható. Ezzel a gondolatmenettel ténylegesen a nem kiszámítható számok létezését lehet megmutatni. Az érvelésnek pontosan ezt a vonalát követi Turing bizonyítása, amellyel, mint ahogy az előző fejezetben elmondtuk, olyan problémák létezését mutatta meg, amelyek nem oldhatók meg algoritmikusan. A későbbiekben az átlós metszés más alkalmazásait is látni fogjuk."...
A valós számok „valóssága”


Tegyük most félre a kiszámíthatóság fogalmát. A valós számokat azért hívják „valósaknak”, mert úgy tetszik, ilyen eredményeket adnak a távolság, szög, idő, energia, hőmérséklet vagy számos egyéb geometriai és fizikai mennyiség mérései. Ám az absztrakt módon definiált „valós számok” és a fizikai mennyiségek kapcsolata nem annyira világos, mint ahogy azt képzelnénk. A valós számok inkább egy „matematikai idealizáció” eredményei, és nem valamiféle aktuális, fizikailag objektív mennyiség mérőszámai. A valós számok rendszerének megvan például az a sajátossága, hogy két tetszőlegesen közel levő között mindig van egy harmadik. Egyáltalán nem világos, hogy a fizikai távolságok vagy idők rendelkeznek-e ezzel a tulajdonsággal. Ha két pont közötti fizikai távolságot egyre tovább osztunk fel kisebb részekre, akkor végül olyan kis skálához érhetünk, amelyen maga a távolság fogalma elvesztheti a közönséges értelemben vett jelentését. Azt sejtik, hogy a „kvantumgravitáció” skáláján, egy szubatomi részecske méreténél 1020-szor kisebb távolságon34 valóban ez a helyzet. Ám hogy minden valós számot felsoroljunk, ahhoz ennél akárhányszor kisebb skálákra is el kellene mennünk: például egy részecske méreténél 10200-szor, 102000-szer vagy 1010200-szor kisebbekre. Egyáltalán nem világos, hogy van-e fizikai értelmük az ilyen abszurdul kicsi skáláknak. Hasonló megjegyzés vonatkozhat a megfelelően kicsi időtartamokra.

A fizikában a valós számok rendszerét matematikai használhatósága, egyszerűsége és eleganciája miatt választjuk, valamint azért, mert nagyon széles tartományban összhangban van a távolság és idő fizikai fogalmával. Nincs szó arról, hogy minden tartományban egyezik ezekkel a fizikai fogalmakkal. Jól látható, hogy a távolság és idő nagyon kis skáláin nincs meg ez az összhang."...
Tartsunk egy kis szünetet, hogy méltányolhassuk az általánosítás nagyságát, melynek során a racionális számoktól eljutottunk a valósakig.
Elsőre azt gondolhatnánk, hogy már az egészek száma is nagyobb a természetes számokénál, mert minden természetes szám egész, míg egyes egészek (a negatívak) nem természetes számok; hasonlóképpen azt is gondolhatnánk, hogy a törtek száma nagyobb, mint az egészeké. Azonban ez nem így van. A végtelen számok szép és hatékony elmélete szerint, amelyet az igen eredeti orosz-német matematikus, Georg Cantor tett közzé az 1800-as évek végén, a törtek, az egészek és a természetes számok teljes száma ugyanaz az ℵ0-lal („alef null”) jelölt végtelen szám. (Érdemes megjegyezni, hogy már 250 évvel korábban, a korai 1600-as években voltak hasonló elképzelései a nagy itáliai fizikusnak és csillagásznak, Galileo Galileinek. Néhány más eredményét az 5. fejezetben felidézzük.) Hogy az egészek száma ugyanannyi, mint a természetes számoké, azt a következő „egy-egy értelmű megfeleltetésből” láthatjuk:"
"Átlós eljárásunk ad tehát egy valós számot, de ez nem kiszámítható. Ezzel a gondolatmenettel ténylegesen a nem kiszámítható számok létezését lehet megmutatni. Az érvelésnek pontosan ezt a vonalát követi Turing bizonyítása, amellyel, mint ahogy az előző fejezetben elmondtuk, olyan problémák létezését mutatta meg, amelyek nem oldhatók meg algoritmikusan. A későbbiekben az átlós metszés más alkalmazásait is látni fogjuk."
"Kiderül, hogy a Természet figyelemre méltóan kegyes hozzánk, és úgy látszik, hogy ugyanazok a valós számok, amelyekhez a mindennapi vagy annál nagyobb skálájú dolgok leírásánál hozzászoktunk, hasznosságukat az atomoknál sokkal kisebb skálákon is megtartják. Biztosan lemehetünk egy szubatomi részecske, mondjuk egy elektron vagy egy proton „klasszikus” átmérőjének századánál is kisebb tartományra, és látszólag le egészen a „kvantumgravitáció skálájáig”, az előző részecskénél húsz nagyságrenddel kisebb távolságokig! Egészen rendkívüli extrapoláció ez a tapasztalattól elindulva. A valós számokkal leírható távolság megszokott fogalma érvényesnek látszik a legtávolabbi kvazárokig és azokon is túl, átfogva legalább 1042, de talán 1060 métert vagy még szélesebb tartományt. A valós számok rendszerének alkalmasságát ritkán kérdőjelezik meg. Miért ez a nagy bizalom e számok iránt a fizika pontos leírásánál, amikor használhatóságukra vonatkozó kezdeti tapasztalataink viszonylag korlátozott tartományra terjednek? Ez a – esetleg méltatlanra pazarolt – bizalom (noha ezt ritkán ismerik fel) a valós számok rendszerének logikai eleganciáján, következetességén és matematikai erején kell nyugodjék, nem feledkezve meg a Természet titkos matematikai harmóniájába vetett hitről. "...
Komplex számok


A valós számok rendszerének, mint kiderül, nincs monopóliuma a matematikai erő és elegancia területén. Sőt elég kényelmetlen, hogy négyzetgyököt csak pozitív számból (vagy nullából) lehet vonni, negatívból nem. Matematikai szempontból – és egy pillanatra félretéve minden kérdést a fizikai világgal való közvetlen kapcsolatról – rendkívül kényelmes, ha a negatív számokból ugyanúgy négyzetgyököt tudunk vonni, mint a pozitívakból. Posztuláljunk vagy „gondoljunk ki” egyszerűen egy négyzetgyököt a –1 számnak. Ezt az „i” szimbólummal fogjuk jelölni, tehát i2 = –1.
Most, hogy a –1-nek már van négyzetgyöke, nem kerül nagy erőfeszítésbe, hogy minden valós számnak megadjuk a négyzetgyökét. Ha a pozitív valós szám, akkor az
Vegyük észre, hogy amikor e mennyiségeket képeztük, megengedtük, hogy összeadjunk valós és képzetes számokat, és hogy a képzetes számokat tetszőleges valós számmal megszorozzuk (vagy nullától különböző valós számmal elosszuk, ami ugyanaz, mint a reciprokkal való szorzás). Az eredményül kapott objektumokat nevezzük komplex számoknak. Egy komplex szám a + ib
Vegyük észre, hogy amikor e mennyiségeket képeztük, megengedtük, hogy összeadjunk valós és képzetes számokat, és hogy a képzetes számokat tetszőleges valós számmal megszorozzuk (vagy nullától különböző valós számmal elosszuk, ami ugyanaz, mint a reciprokkal való szorzás). Az eredményül kapott objektumokat nevezzük komplex számoknak. Egy komplex szám a + ib

alakú, ahol a és b valós számok, a komplex számnak rendre a valós része és a képzetes része. Két ilyen szám összeadásának és összeszorzásának szabályai az (iskolai) algebra szokásos szabályait követik, kiegészítve az i2 = –1 szabállyal:
...Figyelemre méltó dolog történik most! A számoknak ezt a rendszerét azért vezettük be, hogy a négyzetgyökvonást mindig el tudjuk végezni. A célt elértük, bár még ez sem nyilvánvaló. Am ennél jóval több is teljesül: köbgyökök, ötödik gyökök, kilencvenkilencedik gyökök, π-edik gyökök, (1 + i)-edik gyökök stb. mind büntetlenül képezhetők (amint azt a nagy tizennyolcadik századbeli matematikus, Leonhard Euler képes volt megmutatni). A komplex számok mágiájának másik példájaként vizsgáljuk meg a trigonometria egyik, valamivel bonyolultabban kinéző képletét, amelyet meg kellett tanulnunk az iskolában; két szög összegének szinusza és koszinusza,sin(A + B) = sin A cos B + cos A sin B,


cos(A + B) = cos A cos B – sin A sin B,
nem más, mint rendre a képzetes és valós része a sokkal egyszerűbb (és sokkal jobban megjegyezhető!)


eA+B = eAeB


komplex egyenletnek.35 Itt mindössze az



eiA = cos A + i sin A

„Euler-formulát” kell ismernünk (a 16. századbeli jelentős angol matematikus, Roger Cotes is felállította sok évvel Euler előtt), amelyet behelyettesítünk az előző egyenletbe. Az eredmény acos(A + B) + i sin(A + B) = (cos A + i sin A)(cos B + i sin B)
kifejezés, a szorzásokat a jobb oldalon elvégezve az idézett trigonometriai összefüggéseket kapjuk.



Mi több, minden


a0 + a1z + a2z2 + a3z3 + … + anzn = 0

algebrai egyenletnek (a0, a1, a2, … , an komplex számok, an ≠ 0) van z komplex szám megoldása. Van például egy z komplex szám, amely kielégíti a

z102 + 999z33 – πz2 = –417 + i
...Figyelemre méltó dolog történik most! A számoknak ezt a rendszerét azért vezettük be, hogy a négyzetgyökvonást mindig el tudjuk végezni. A célt elértük, bár még ez sem nyilvánvaló. Am ennél jóval több is teljesül: köbgyökök, ötödik gyökök, kilencvenkilencedik gyökök, π-edik gyökök, (1 + i)-edik gyökök stb. mind büntetlenül képezhetők (amint azt a nagy tizennyolcadik századbeli matematikus, Leonhard Euler képes volt megmutatni). A komplex számok mágiájának másik példájaként vizsgáljuk meg a trigonometria egyik, valamivel bonyolultabban kinéző képletét, amelyet meg kellett tanulnunk az iskolában; két szög összegének szinusza és koszinusza,sin(A + B) = sin A cos B + cos A sin B,
nem más, mint rendre a képzetes és valós része a sokkal egyszerűbb (és sokkal jobban megjegyezhető!)
eA+B = eAeB
komplex egyenletnek.35 Itt mindössze az
eiA = cos A + i sin A
Mi több, minden
a0 + a1z + a2z2 + a3z3 + … + anzn = 0
algebrai egyenletnek (a0, a1, a2, … , an komplex számok, an ≠ 0) van z komplex szám megoldása. Van például egy z komplex szám, amely kielégíti a
z102 + 999z33 – πz2 = –417 + i
egyenletet, bár ez egyáltalán nem nyilvánvaló! Az állítást olykor az „algebra alaptételeként” idézik."...
"1831-ben a nagy matematikus és természettudós, Carl Friedrich Gauss meglepően eredeti gondolatmenettel megadta az első általános bizonyítást. Ennek kulcsfontosságú tényezője volt a komplex számok geometriai ábrázolása, és azután egy topológiai36 érvelés.


Valójában nem Gauss használta először a komplex számok geometriai leírását. "
...Bolyai és Gauss.
" A hagyományos (bár történetileg egyáltalán nem pontos) terminológiával összhangban a komplex számok szokásos geometriai ábrázolására mint Argand-síkra fogok hivatkozni.


 Az Argand-sík közönséges euklideszi sík, szabványos x és y derékszögű koordinátákkal, x a vízszintes távolságot jelöli (pozitív jobbra, negatív balra), y a függőlegeset (pozitív felfelé, negatív lefelé). A
Az Argand-sík közönséges euklideszi sík, szabványos x és y derékszögű koordinátákkal, x a vízszintes távolságot jelöli (pozitív jobbra, negatív balra), y a függőlegeset (pozitív felfelé, negatív lefelé). A z = x + iy
z = x + iy
Valójában nem Gauss használta először a komplex számok geometriai leírását. "
...

komplex számot az a pont ábrázolja az Argand-síkon, amelynek koordinátái



(x, y)


(lásd a 3.8. ábrát). Jegyezzük meg, hogy a 0-t (mint komplex számot) a koordináták kezdőpontja ábrázolja, az 1-et egy speciális pont az x tengelyen.
komplex számot az a pont ábrázolja az Argand-síkon, amelynek koordinátái
(x, y)
(lásd a 3.8. ábrát). Jegyezzük meg, hogy a 0-t (mint komplex számot) a koordináták kezdőpontja ábrázolja, az 1-et egy speciális pont az x tengelyen.
"Az Argand-sík lehetővé teszi, hogy komplex számcsaládunkat geometriailaghasznos képbe szervezzük. Ez a dolog nem igazán új számunkra. Már hozzászoktunk ahhoz, hogy a valós számokat geometriai képbe lehet rendezni, nevezetesen egy egyenes vonalra, amely mindkét irányban végtelen. A vonal egyik kiválasztott pontjára a 0, egy másikra az 1 címkét akasztjuk. A 2 pont úgy helyezkedik el, hogy távolsága az 1-től ugyanakkora, mint az 1 és a 0 távolsága; az 1/2 a középső pont 0 és 1 között; a –1 pont úgy helyezkedik el, hogy a 0 félúton legyen közötte és 1 között; stb., stb. A valós számok ily módon megjelenített halmazát valós számegyenesnek nevezzük. A komplex számoknál valójában két valós számot használunk koordinátáknak, az a + ib komplex számnál a-t és b-t. Ezek a számpárok megadják a pontok koordinátáit egy síkon
u=1+i1,3; v=-2+i; w=-1,5-i0,4komplex számokat.
A komplex számok összeadásának és szorzásának alapvető algebrai műveletei most világos geometriai formát kapnak. Nézzük először az összeadást! Legyen u és v az Argand-síkon az előzőek szerint ábrázolt két komplex szám!
Ezzel ekvivalens módon azt mondhatjuk, hogy a 0, v és uv által alkotott háromszög hasonló (és hasonló állású) a 0, 1 és u által alkotott háromszöggel.
Vektoralgebra, műveletek vektorokkal.Gyuri, a legidősebb a kilenc unoka közül, mindannyiunk által elismert és elfogadott "primus inter pares"-ünk boldog izgalommal és lekesedéssel mutatja - egyetemi jegyzetekhez hasonlító,puritán kinézetű matematika könyveit, talán a téli szünetben. Ő másodikos én elsős. Ő matematika tagozatos osztályba jár Debrecenben. Az az ország egyik legjobb gimnáziuma volt akkor, és valószínűleg az most is. Ámultan hallgatom és nézem, hogy mikről tanulnak. Biztosan a komplex számokat is mutogatja, amelyekről mi még az egyetemen sem tanultunk, vagy ha igen, inkább csak "lábjegyzetként". Igazából Penrosenek ez a könyve hozta el számomra felfogható távolságra a komplex számokat. Itt és most, ahogy olvasom....
komplex számokat.
A komplex számok összeadásának és szorzásának alapvető algebrai műveletei most világos geometriai formát kapnak. Nézzük először az összeadást! Legyen u és v az Argand-síkon az előzőek szerint ábrázolt két komplex szám!
A Mandelbrot-halmaz felépítése
Most már megnézhetjük, mi a Mandelbrot-halmaz definíciója.
Legyen z tetszőleges komplex szám. Ezt az Argand-síkon egy pont ábrázolja. Tekintsük most a
z → z2 + c leképezést, amely z-t egy új komplex számmal helyettesíti, c egy másik, rögzített (azaz adott) komplex szám. A z2 + c számot az Argand-síkon egy új pont ábrázolja. Ha például c az 1,63 – i 4,2 szám, akkor a leképezés z → z2 + 1,63 – i 4,2, így például 3 a 32 + 1,63 – i 4,2 = 9 + 1,63 – i 4,2 = 10,63 – i 4,2 számmal, –2,7 + i 0,3 a (–2,7 + i 0,3)2 + 1,63 – i 4,2 = (–2,7)2 – (0,3)2 + 1,63 + i{2(–2,7)(0,3) – 4,2} = 8,83 – i 5,82 számmal helyettesítendő. Amikor a számok bonyolultak, akkor a számítást legjobb elektronikus számítógéppel végezni.Na már most, bármi is c, a 0 szám ebben a leképezésben az adott c számba megy át. És mi történik c-vel? Ezt a c2 + c számmal kell helyettesíteni. Folytassuk a sort, és alkalmazzuk a helyettesítést a c2 + c számra; a következőt kapjuk: (c2 + c)2 + c = c4 + 2c3 + c2 + c. Iteráljuk a leképezést még egyszer, alkalmazzuk most a fenti számra, (c4 + 2c3 + c2 + c)2 + c = c8 + 4c7 + 6c6 + 6c5 + 5c4 + 2c3 + c2 + c, azután újra erre a számra stb. A komplex számok egy 0-val induló sorozatát kapjuk: 0, c, c2 + c, c4 + 2c3 + c2 + c, … . Ha most az adott c komplex számot megfelelően választjuk, akkor az így kapott számsorozat soha nem vándorol túl messze az Argand-síkon a kezdőponttól; pontosabban megfogalmazva: c ilyen megválasztása esetén a sorozat korlátos marad, azaz minden tagja egy kezdőpont körüli rögzített körben fekszik (lásd 3.12. ábra). "A Mandelbrot-halmaz, azaz Tor’Bled-Nam világának fekete tartománya az Argand-síknak pontosan az a tartománya, amelyben lévő c pontokra a sorozat korlátos marad. A fehér tartomány azokat a c pontokat tartalmazza, amelyekre a sorozat nem korlátos. A korábban látott részletes képeket számítógépek kivitt adataiból rajzolták. A számítógép módszeresen végigfut a c komplex szám lehetséges értékein, mindegyikre kiszámítja a 0, c, c2 + c, … sorozatot, és alkalmas kritériumok alapján eldönti, hogy a sorozat korlátos marad-e vagy sem. Ha igen, akkor a számítógép intézkedik, hogy a képernyőre a c-nek megfelelő pontba fekete pötty kerüljön. Ha nem korlátos, akkor a számítógép fehér pontot rak ki. Végül is a vizsgált tartomány összes pontjáról eldönti, hogy azt fehérre vagy feketére színezze.
Most már megnézhetjük, mi a Mandelbrot-halmaz definíciója.
Legyen z tetszőleges komplex szám. Ezt az Argand-síkon egy pont ábrázolja. Tekintsük most a
A matematikai fogalmak platóni valósága?
A Mandelbrot-halmaz bonyolultsága igen figyelemreméltó, különösen annak tükrében, hogy e halmaz definíciója a matematikai definíciókhoz képest meglepően egyszerű. Az is igaz, hogy e halmaz általános szerkezete nem nagyon érzékeny a választott z → z2 + c leképezés pontos algebrai alakjára. Sok más iterált komplex leképezés (például z →z3 + iz2 + c) rendkívül hasonló szerkezeteket ad (feltéve, hogy az induláshoz megfelelő számot választunk – esetleg nem 0-t, hanem olyan számot, amelynek értékét világos matematikai szabály adja meg minden megfelelően választott leképezésre). Van ezeknek a „Mandelbrot”-szerkezeteknek egyfajta, az iterált komplex leképezésekkel összefüggő, univerzális vagy abszolút jellegük. Az ilyen szerkezetek tanulmányozása a matematikán belül önmagában érdekes, komplex dinamikai rendszerekként szoktak hivatkozni rájuk."
Mennyire „valóságosak” a matematikusok világának objektumai? Az egyik nézőpontból úgy látszik, hogy egyáltalán nem beszélhetünk valóságról velük kapcsolatban. A matematikai objektumok csupán fogalmak; agyszülemények, amelyeket a matematikusok csinálnak, gyakran ugyan a körülöttünk lévő világ külső megjelenése és látszólagos rendje által ösztönözve, de mégis csak szellemi idealizációk. Lehetnek-e mások, mint csupán az emberi értelem önkényes építményei? Ugyanakkor gyakran mély valóság látszik e matematikai fogalmak körül, amely messze túlmegy bármelyik matematikus szellemi termékein. Mintha valami az emberi gondolkodást örök külső igazságok felé vezetné, amelyeknek megvan a saját valóságuk, és amelyeket csak részlegesen ismer fel bármelyikünk.
4. Igazság, bizonyítás, meglátás
Hilbert programja a matematikában
Hogy a kérdést egyszerűsítsük, tekintsük csupán a matematikai igazságot. Hogyan alakítjuk ki ítéleteinket – talán még „bizonyos” tudásunkat is – a matematikai kérdésekben? Itt legalább sokkal világosabbak a dolgok. Nem lehet kérdéses, hogy az adott esetben mi igaz, és mi hamis – vagy mégis? Mi valójában a matematikai igazság?
A matematikai igazság kérdése nagyon messzire nyúlik vissza, a korai görög filozófusok és matematikusok idejére és még régebbre. Egyes nagyon nagy tisztába tételek és meglepő új meglátások azonban nagyjából az elmúlt száz év eredményei. Ezeket az új fejleményeket próbáljuk megérteni. A problémák egészen alapvetőek, és azt a kérdést érintik, hogy vajon gondolkodási folyamatunk valóban lehet-e teljesen algoritmikus természetű. Fontos, hogy ezekkel tisztába jöjjünk.
A 19. század vége felé a matematika nagy lépéseket tett előre, részben azért, mert a matematikai bizonyításnak egyre több és több hatásos módszere fejlődött ki. (David Hilbert és Georg Cantor, akikkel korábban már találkoztunk, és a kiváló francia matematikus, Henri Poincaré, akivel később fogunk megismerkedni, ők hárman voltak e fejlődés élharcosai.) A matematikusok biztonságot szereztek e hatékony módszerek használatában. Sok ilyen módszer használta a végtelen számú tagot tartalmazó halmaz40 fogalmát, és a bizonyítások gyakran éppen azért voltak sikeresek, mert a halmazokat valódi „dolgoknak” – teljes, létező egészeknek – tudták tekinteni, nem csupán potenciális lehetőségeknek.
Ez a magabiztosság azonban megtört, amikor 1902-ben a brit logista és filozófus, Bertrand Russell előállt ma már híres paradoxonjával (amelyet már Cantor is előre látott, lévén közvetlen leszármazottja az ő „átlós metszés” eljárásának).
Na már most, mi a Russell-paradoxon? Az egy R halmazra vonatkozik, amelynek definíciója a következő: R a halmaza minden halmaznak, amely nem eleme saját magának. R így halmazok bizonyos gyűjteménye; annak feltétele, hogy egy X halmaz a gyűjteményhez tartozzék, az, hogy ő maga ne legyen saját elemei között.Abszurd feltételezés-e az, hogy egy halmaz eleme saját magának? Nem igazán. Tekintsük például a végtelen (végtelen sok elemű) halmazok I halmazát. Biztos, hogy végtelen sok különböző végtelen halmaz van, így I maga végtelen. I tehát valóban hozzátartozik saját magához! Miért van akkor az, hogy Russell elgondolása paradoxonhoz vezet? Azt kérdezzük: Russell R halmaza eleme-e saját magának vagy sem? Ha nem, akkor R-hez kell tartozzon, mert R pontosan azokat a halmazokat tartalmazza, amelyek nem elemei saját maguknak. Ezért R végül is R-hez tartozik – ami ellentmondás. Ha viszont R eleme saját magának, akkor mivel „saját maga” valójában R, ezért olyan halmazhoz tartozik, amelynek elemeire az jellemző, hogy nem elemei saját maguknak, azaz végül is R nem eleme saját magának – ami megint ellentmondás!42Ez a gondolatmenet nem volt komolytalan. Russel csupán ugyanazt a típusú, nagyon általános, matematikai halmazelméleti okfejtést használta nagyon szélsőséges formában, mint amelyet a matematikusok kezdtek bizonyításaikban alkalmazni. A dolgok nyilvánvalóan kicsúsztak a matematikusok kezeiből, és sürgetővé vált, hogy sokkal pontosabban fogalmazzák meg, milyen típusú okfejtés megengedett, és milyen nem. Az feltétlenül szükséges, hogy a megengedett gondolatmenetben ne legyen ellentmondás, és hogy csak igaz állításokat engedjen meg levezetni előzőleg igaznak ismert állításokból.Russell munkatársával, Alfred North Whiteheaddel nekilátott, hogy kidolgozza axiómáknak és eljárási szabályoknak egy nagymértékben formális matematikai rendszerét.A szabályokat gondosan válogatták, hogy megakadályozzák a paradoxon jellegű gondolatmeneteket, amilyen a Russell-paradoxonhoz is vezetett. A Russell és Whitehead által készített különleges rendszer nagyszabású munka volt. Ám sok fáradsággal járt, és eléggé korlátozta a megengedett matematikai okfejtések típusait. David Hilbert, a nagy német matematikus, akivel először a 2. fejezetben találkoztunk, belekezdett egy sokkal jobban használható és átfogóbb rendszerbe. Minden korrekt matematikai típusú gondolatmenetet be kívánt illeszteni a matematika minden területéről. Mi több, Hilbert arra törekedett, hogy bizonyítani lehessen, hogy a rendszer ellentmondásmentes. Így a matematika egyszer s mindenkorra megtámadhatatlan alapzatra kerülne.Hilbertnek és követőinek reményei azonban semmivé váltak, amikor 1931-ben a 25 éves ragyogó osztrák matematikai logista, Kurt Gödel egy olyan meglepő tétellel állt elő, amely hatásosan rombolta le Hilbert programját. Gödel azt mutatta meg, hogy axiómáknak és eljárási szabályoknak tetszőleges ilyen pontos („formális”) matematikai rendszere, feltéve hogy elég széles, hogy tartalmazza egyszerű aritmetikai propozíciók (állítások) leírásait (mint a 2. fejezetben tárgyalt „Fermat utolsó tétele”), és feltéve hogy ellentmondásmentes, kell tartalmazzon olyan állítást, amely a rendszeren belül megengedett módokon nem bizonyítható és nem cáfolható. Az ilyen állítások igazsága tehát a jóváhagyott eljárásokkal „nem dönthető el”. Gödel ténylegesen meg tudta mutatni, hogy magának az axiómarendszer következetességének állítása, átalakítva megfelelő aritmetikai állítássá, szintén ilyen „eldönthetetlen” állítás. Fontos, hogy megértsük ezen „eldönthetetlenség” természetét. Látni fogjuk, miért hatolt le Gödel bizonyítása egészen a magjáig Hilbert programjának. Látni fogjuk azt is, hogyan tesz képessé Gödel tétele a meglátás felhasználásával arra, hogy túllépjünk bármely speciális formális matematikai rendszer korlátain. Ennek megértése döntő lesz sok elkövetkező fejtegetésünk szempontjából.
Hogy a kérdést egyszerűsítsük, tekintsük csupán a matematikai igazságot. Hogyan alakítjuk ki ítéleteinket – talán még „bizonyos” tudásunkat is – a matematikai kérdésekben? Itt legalább sokkal világosabbak a dolgok. Nem lehet kérdéses, hogy az adott esetben mi igaz, és mi hamis – vagy mégis? Mi valójában a matematikai igazság?
A matematikai igazság kérdése nagyon messzire nyúlik vissza, a korai görög filozófusok és matematikusok idejére és még régebbre. Egyes nagyon nagy tisztába tételek és meglepő új meglátások azonban nagyjából az elmúlt száz év eredményei. Ezeket az új fejleményeket próbáljuk megérteni. A problémák egészen alapvetőek, és azt a kérdést érintik, hogy vajon gondolkodási folyamatunk valóban lehet-e teljesen algoritmikus természetű. Fontos, hogy ezekkel tisztába jöjjünk.
Formális matematikai rendszerek
Gödel tétele
Megszámoztunk minden egyváltozós propozíciós függvényt, ezért a most leírtnak is kell legyen száma. Legyen ez k! Propozíciós függvényünk a listán a k-adik. Így ~ ∃ x[Πx bizonyítja Pw(w)-t] = Pk(w). Vizsgáljuk most e függvényt a speciális w = k érték mellett. Azt kapjuk, hogy ~ ∃ x[Πx bizonyítja Pk(k)-t] = Pk(k).A speciális Pk(k) propozíció egy tökéletesen jól definiált (szintaktikusan helyes) aritmetikai állítás. Van-e bizonyítása formális rendszerünkön belül? Van-e tagadásának, ~ Pk(k)-nak bizonyítása? A válasz mindkét kérdésre „nem” kell legyen. Ezt úgy láthatjuk, hogy megvizsgáljuk a Gödel-eljárás mögött húzódó jelentést. Noha Pk(k) aritmetikai propozíció, konstrukciója szerint azt állítja, ami a bal oldalon áll: „a rendszeren belül a Pk(k) propozíciónak nincs bizonyítása”. Ha axiómáinkat és eljárási szabályainkat gondosan fektettük le, és ha a számozást helyesen végeztük, akkor a rendszeren belül ennek a Pk(k)-nak nem lehet bizonyítása. Mert ha lenne, akkor Pk(k) állítás „jelentése”, nevezetesen, hogy nincs bizonyítás, hamis lenne, így Pk(k) mint aritmetikai propozíció hamis kellene legyen. Formális rendszerünk nem lehet olyan rosszul felépített, hogy megengedje hamis propozíciók bizonyítását! Ezért a helyzet az kell legyen, hogy Pk(k)-nak ténylegesen nincs bizonyítása. Azonban pontosan ez az, amit Pk(k) mondani próbál nekünk. Ezért amit Pk(k) mond, az igaz állítás kell legyen, így Pk(k), mint aritmetikai propozíció igaz kell legyen. Találtunk egy igaz propozíciót, amelynek a rendszeren belül nincs bizonyítása!Mi a helyzet tagadásával, ~Pk(k)-val? Az előbbiekből következik, hogy ennek sem lehet bizonyítása. Épp most állapítottuk meg, hogy ~Pk(k) hamis kell legyen (mert Pk(k) igaz), és hamis propozíciókat a feltevés szerint a rendszeren belül nem tudunk bebizonyítani! Így sem Pk(k), sem ~ Pk(k) nem bizonyítható formális rendszerünkben. Ez Gödel tétele.
Matematikai meglátás
Vegyük észre, hogy itt most valami nagyon figyelemreméltó dolog történt. Az emberek gyakran gondolnak a Gödel-tételre negatívumként – mint amely a formális matematikai gondolkodás szükségszerű korlátait mutatja meg. Akármilyen átfogónak is gondoljuk rendszerünket, mindig lesznek propozíciók, amelyek kiszöknek a hálóból. De kell-e izgasson bennünket ez a speciális Pk(k) propozíció? A fenti gondolatmenet során megállapítottuk, hogy Pk(k) igaz állítás! Sikerült valahogy meglátnunk, hogy Pk(k) igaz, annak ellenére, hogy a rendszeren belül formálisan nem bizonyítható. A szigorú matematikai formalistáknak valóban aggódniuk kell, mert éppen a fenti gondolatmenettel állapítottuk meg, hogy a formalista „igazság”-fogalom szükségképpen nem teljes. Akármilyen (következetes) formális rendszert használunk is az aritmetikára, lesznek olyan állítások, amelyekről láthatjuk, hogy igazak, de amelyekhez az előbb leírt formalista eljárással nem tudjuk hozzárendelni az igaz igazságértéket. A szigorú formalista talán úgy próbálhatja ezt megkerülni, hogy egyáltalán nem beszél az igazság fogalmáról, hanem csak egy rögzített formális rendszeren belüli bizonyíthatóságról. Ez azonban nagyon korlátozónak látszik. E nézőpontot elfogadva még az előző Gödel-féle érvelést sem tudnánk elmondani, mert annak lényeges részei használnak meggondolásokat arról, mi igaz, és mi nem igaz.45
A meglátás, amely által arra következtettünk, hogy a Pk(k) Gödel-propozíció valóban igaz állítás az aritmetikában, általános példája annak az eljárásnak, amelyet a logisták tükrözési elvként ismernek: „tükrözve” az axiómarendszer és az eljárási szabályok értelmét, és meggyőződve arról, hogy ezekkel valóban érvényes módon juthatunk el matematikai igazságokig, képesek lehetünk e meglátást újabb igaz matematikai állításokba kódolni, amelyek magukból az axiómákból és szabályokból nem vezethetők le. Pk(k) igazságának leszármaztatása, mint előbb körvonalaztam, ilyen elvre támaszkodott. Egy másik, az eredeti Gödel-féle érvelés számára lényeges (bár az előzőekben nem megadott) tükrözési elvre támaszkodik az, ahogy új matematikai igazságokat származtatnak abból a tényből, hogy egy axiómarendszer, amelyet matematikai igazságok előállítására már érvényesnek hiszünk, ténylegesen konzisztens. A tükrözési elvek gyakran tartalmaznak végtelen halmazokra vonatkozó gondolatmeneteket, és használatuknál mindig vigyáznunk kell arra, hogy ne kerüljünk túl közel az olyan jellegű érveléshez, amely Russell-típusú paradoxonhoz vezethet. A tükrözési elvek szolgáltatják a formalista gondolkodás antitézisét. Ha óvatosak vagyunk, akkor ezek képessé tesznek arra, hogy kiszökjünk egy formális rendszer merev falai közül és új matematikai meglátásokhoz jussunk, amelyek korábban nem látszottak elérhetőnek. Matematikai irodalmunkban sok teljesen elfogadható eredmény van, amelyek bizonyításai olyan meglátásokat követelnek, amelyek távol esnek az aritmetikára használatos szabványos formális rendszerek eredeti szabályaitól és axiómáitól. Mindez azt mutatja, hogy a szellemi eljárások, amelyek segítségével a matematikusok meghozzák ítéleteiket, nem egyszerűen valamely speciális formális rendszer eljárásaiban gyökereznek. Látjuk a Pk(k) Gödel-propozíció érvényességét, bár az axiómákból levezetni nem tudjuk. Az a fajta „látás”, amelyet egy tükrözési elv magában foglal, olyan matematikai meglátást követel, amely nem eredménye tisztán algoritmikus műveleteknek, amelyeket egy formális matematikai rendszerbe lehetne kódolni. Erre a 10. fejezetben majd visszatérünk.Az Olvasó észrevehet bizonyos hasonlóságot a Pk(k) igazságát, mégis „bizonyíthatatlanságát” megalapozó érvelés és a Russell-paradoxon gondolatmenete között. Van hasonlóság Turing bizonyításával is, amely megállapítja, hogy nem létezik olyan Turing-gép, amely megoldja a megállási problémát. E hasonlóságok nem véletlenek. A három között erős történeti szál teremt kapcsolatot. Turing Gödel munkájának tanulmányozása után találta meg bizonyítását. Gödel jól ismerte a Russell-paradoxont, és képes volt az ilyen paradox gondolatmenetet érvényes matematikai bizonyítássá alakítani. (Mindezek a gondolatmenetek Cantornak az előző fejezetben leírt „átlós metszés”-éből származnak.)
Miért fogadjuk el Gödel és Turing bizonyításait, noha a Russell-paradoxonhoz vezető gondolatmenetet el kellett vetnünk? Az előbbiek sokkal világosabbak és mint matematikai bizonyítások kifogástalanok, míg a Russell-paradoxon ködösebb, „óriási” halmazokkal operáló érvelésre támaszkodik. Ám el kell ismernünk, hogy a különbségek nem annyira tiszták, mint amennyire szeretnénk. A különbségek világossá tételének szándéka komoly hajtóereje volt a formalizmus egész elképzelésének. Gödel bizonyítása azt mutatja, hogy a szigorú formalista nézőpont nem tartható igazán; mégsem kínál egészében megbízható, alternatív nézőpontot. A kérdés szerintem nem megoldott. A matematikában jelenleg elfogadott eljárás48 az olyan típusú „óriási” halmazokat használó érvelés elkerülésére, mint amilyen a Russell-paradoxonhoz vezet, nem teljesen kielégítő.
Mi több, határozottan formalista módon igyekeznek megfogalmazni – vagy másképpen olyan formában, amely nem győz meg teljesen arról, hogy nem fordulhatnak elő ellentmondások.Akármi is a helyzet, én úgy látom, hogy a Gödel-féle bizonyításnak világos következménye az, hogy a matematikai igazság fogalma nem zárható be formális sémába, az túlmegy a puszta formalizmuson. Ez talán még a Gödel-tétel nélkül is világos. Mert hogyan döntjük el, mely axiómákat és eljárási szabályokat fogadjuk el, amikor egy formális rendszert próbálunk felállítani?
Döntésünkben mindig intuitív megértésünk kell vezessen, mi az, ami „magától értetődően igaz”, ha ismerjük a rendszer szimbólumainak „értelmét”. Hogyan döntjük el, milyen formális rendszereket ésszerű elfogadni – összhangban intuitív érzéseinkkel a „magától értetődő”-ről és „értelem”-ről – és milyeneket nem? Az önkonzisztencia követelménye erre bizonyára nem megfelelő. Sok önkonzisztens rendszer lehet ebben az értelemben nem „ésszerű”, ezeknél az axiómák és eljárási szabályok olyan állítások, amelyeket mint hamisakat vagy esetleg értelmetleneket elvetünk. „Magától értetődő” és „értelem” olyan fogalmak, amelyekre még a Gödel-tétel nélkül is szükség volna.A Gödel-tétel nélkül azonban elképzelhetnénk, hogy a „magától értetődő” és „értelem” intuitív fogalmait csupán a formális rendszer felállításánál alkalmazzuk, utána, az igazság meghatározására szolgáló tiszta matematikai érvelésben eltekintünk tőlük. Ekkor, a formalista nézettel összhangban, ezek a „homályos” intuitív fogalmak a matematikus előzetes gondolkodásának részeként jutnának szerephez, útmutatóként az alkalmas formális érvelés megtalálásához; de nem játszanának szerepet a matematikai igazság tényleges bemutatásában.
Gödel tétele azt mutatja, hogy ez a nézőpont egy matematikai alapfilozófiában nem igazán tartható. A matematikai igazság fogalma túlmegy a formalizmus egész koncepcióján. Van benne valami abszolút és „istenadta”. Ez az, amiről az előző fejezet végén tárgyalt matematikai platonizmusban szó van. Bármilyen speciális formális rendszer ideiglenes és „ember alkotta” minőséget fejez ki róla. E rendszerek valóban nagyon értékes szerepet játszanak a matematikai vizsgálatokban, de az igazsághoz csak részleges (vagy közelítő) útmutatással szolgálhatnak. Az igazi matematikai igazság túlmegy a csupán ember alkotta konstrukciókon.
Vannak olyan elképzelések is, hogy igazából az univerzum nem más, mint egy matematikai struktúra. Max Tegmark Our Mathematical Universe című könyvében foglalkozik ezzel a gondolattal.
Tény, hogy a matematika valamiért, valahogy a természet lényege. Hogy ez miért lehet így, hogy valamilyen vélt vagy valós konklúzióra juthassunk, kövessük Wigner Jenő gondolatmenetét.
A matematika a mennyiségekből a műveletek által létrehozott csoportokból és tulajdonságokból struktúrákat hoz létre és ezen struktúrák tulajdonságait vizsgálja.
Ez a meghatározás a geometriára is érvényes, hiszen a geometriát is kezelhetjük mennyiségeken és műveleteken keresztül.
Mi a fizika (és gyakorlatilag valamennyi természettudomány)?
A fizika a valóság, a létező világ, a természet leírása. A fizikán keresztül ismerjük meg a valóság alkotó elemeit, tulajdonságait, egymással való kapcsolatát, kölcsönhatásait. A fizika leírja a való világot, tényeket állapít meg a létező dolgokról, megfigyeli a tulajdonságait. Keresi, meghatározza és leírja a való világ építő elemeit, hogyan hatnak egymásra, hogyan kapcsolódnak egymáshoz, hogyan építenek a kölcsönhatások által struktúrákat.
A fizika alapvetően a valósággal foglalkozik, de a fizikát kiterjeszthetjük a nem tapasztalt valóságra is. Például a fizika foglalkozhat a multiverzummal is, de ebben az esetben is a cél a valóság megismerése. A multiverzumot is azért találjuk ki, mert úgy gondoljuk, hogy az a valóság része.
A fizika foglalkozhat alternatív valósággal is, de ebben az esetben is a fizika a megvalósulható valóságot keresi, a fizika feltételezi, hogy ezek az alternatív valóságok létezhetnek.
Fontos tulajdonsága a valóságnak, hogy a kölcsönhatások által létrejött struktúráknak új, a felépítő elemek által nem hordozott tulajdonságai jöhetnek létre.
Előzőleg megállapítja, hogy ugyanez áll a matematikai struktúrák kölcsönhatására is.A matematika absztrakt, a fizika konkrét tudományA fizika konkrét tudomány, mindig valamilyen létező minőségre, dologra vonatkozik. A fizika nem elvonatkoztatható attól a valóságtól, amit tárgyal.
A matematika univerzális, a fizika specifikus tudomány
Mivel a matematika nem kötődik a dolgok minőségéhez, nem is függ tőle. A matematika bármilyen anyagi minőségen alkalmazható. Természetesen nem minden matematikai művelet értelmezhető és ezért nem minden matematikai művelet használható különböző anyagi minőségekre, de ez nem a matematika korlátja, hanem az anyagi világunk jellemzője.
A matematika tisztán teoretikus tudomány, a fizika alapja a megfigyelés.Mivel a matematika nem foglalkozik az anyagi minőséggel, teoretikus, az anyagi világunkat nem figyelembe vevő módon kezelhető, formázható, fejleszthető. A működésének szabálya és korlátja az alapvető logika, a nyilvánvaló igazságok. Mivel a matematikát a valóság nem korlátozza, nem ellentmondásmentes tudomány (Göddel felismerés).A fizika alapja és korlátja a megfigyelés, a létező világ. A fizika fejleszthető teoretikusan, akár csupán a matematika eszközeivel is - ilyenkor szoktunk rácsodálkozni a matematika szerepére a természetben -, mégis a legszebb teória, a leglogikusabb következtetés is bizonyulhat hibásnak a fizikában - ahogy az meg is történik sokszor - ha nem felel meg a valóságnak.
A matematika nem minden értelmezhető művelete értelmezhető művelete a valóságnak is. A valóság ezen tulajdonsága biztosítja egyben azt is, hogy a valóság ellentmondás mentes rendszert alkosson. Ha egy elméleti következtetés a fizikában ellentmondásra vezet, akkor az az elméleti út bizonyosan nem lehet érvényes a valóságban.
A matematikai megismerés eszköze az elméleti következtetés, de az ellentmondás mentesség nem zárható ki.
A fizika lényegét tekintve ugyanazt a feladatot végzi, mint a matematika. Mindkettő elemek összességével foglalkozik. A matematika az elemeken matematikai műveleteket végez, a fizika létező kölcsönhatásokat vizsgál. Mindkettő a műveletekkel-kölcsönhatásokkal létrejött új struktúrák tulajdonságaival foglalkozik.
A fizika annyiban több a matematikánál, hogy a minőséggel is foglalkozik, és ugyanezért kevesebb is nála. A fizika annyiban korlátozottabb a matematikánál, hogy a valóság az összes lehetséges lehetőségeknek egy részhalmaza.
Érdekes és fontos jellemzője mindkét tudománynak, hogy mindkettő lezárhatatlan. Mindkét tudományra jellemző, hogy a műveletek-kölcsönhatások során új rendszerek keletkeznek, új tulajdonságokkal. A fizikának az elméleti korlátját a megvalósult valóság végessége határozza meg, a matematikának nincs ilyen korlátja.
Mi a matematika és a fizika kapcsolata?
A matematika a fizikai megismerés eszköze. Mivel a matematika a mennyiségekkel, a valóság minőségétől független jellemzőjével foglalkozik, a matematikai műveletek érvényesek a fizikában.
Fordítva a kijelentés nem érvényes. A fizika nem eszköze a matematika megismerésének. A valós világ korlátozza a matematika érvényességet. Egy valós anyagi rendszerre nem minden matematikai művelet értelmes vagy értelmezhető. A fizika, a valóság korlátozza, hogy melyek azok a matematikai műveletek, amelyek érvényesek az adott anyagi rendszerre.
Alapvető tulajdonsága a fizikának, hogy azok a matematikai műveletek, amelyek az adott fizikai rendszerre érvényesek, univerzálisan érvényesek. Helytől, időtől, és egyéb körülményektől függetlenül működnek. Ezek a fizikai valóságunk szimmetriái. Ezen szimmetriák azért létezhetnek, mert az adott fizikai kölcsönhatások matematikai leírásában szimmetria létezik, érvényes.
A fizika és a matematika kapcsolata egyirányú. A fizika mindig követi a matematika (aktuálisan érvényes) szabályait, de a fizika, a valóság nem meghatározó korlátja a matematikának. A matematika korlátja a tiszta logika (ha egy bizonyítás lépései igazak, akkor a bizonyítás következménye, eredménye is igaz), kiinduló szabályai a nyilvánvaló, vagy absztrakt igazságok (például, ha két mennyiség különböző, akkor azok nem egyformák, vagy ha két egyenes nem találkozik, akkor nincs közös pontjuk).
A valóság megismerésében egy következtetés lépéseinek igazsága a tiszta logikán kívül (mellett, helyett) a megfigyelés pontatlan eszközeire is támaszkodik, az absztrakt igazságok pedig sokszor értelmezhetetlenek a valóságban (két alma különböző is lehet meg azonos is, és a valóságban nem létezik végtelen hosszúságú, de végtelenül vékony struktúra).
A valós világ, a fizika kölcsönhatásokra épül, a kölcsönhatások a valós világ műveletei. A kölcsönhatások szabályozzák a valós világ működését. A fizikai kölcsönhatásoknak specifikus szabályai vannak. Mivel a kölcsönhatások mennyiségeket is jelentenek, a fizikai kölcsönhatások a matematika eszközeivel leírhatok, azonban mivel a kölcsönhatások specifikusak, speciális jellemzőkkel bírnak, csak bizonyos meghatározott matematikai eszközök használhatók, érvényesek. Ezeknek a specialitásoknak a felismerése adja a fizika, mint tudomány célját, a matematika pedig eszközöket biztosít ennek a megismerésnek.
Miért működik a matematika a valóság megismerésében?
Mivel a valóság mennyiségekre épül, a matematika természetszerűleg alkalmazható a világ megismerésében. A valóságban megvalósuló, létező kölcsönhatásoknak a fizikai mennyiségekre vonatkozó specifikuma szabályozza, határozza meg, hogy mely matematikai műveletek alkalmazhatók az adott anyagi rendszerre. Például, a quantum mechanikában szükséges az irracionális számok használata. Miért? Azért, mert a quantum mechanika kölcsönhatásainak rendszere, struktúrája, szimmetriai megfeleltethető az irracionális számok műveleteinek, a matematikai eszközrendszer struktúrájának. A fizika más területein is hasonló megfeleltetések érvényesek.
A fizika fejlődése a megfigyelésen alapszik. Azonban, ha már képesek vagyunk egy közelítő képet alkotni az adott fizikai rendszerről és a kölcsönhatásairól, a fizika fejlődhet teoretikusan is, a logika eszközei segítségével, de minden új következtetés csak akkor tekinthető érvényesnek, ha a valóság, a megfigyelés támogatja, megfelel a következtetésnek.
A matematika mitől a nyelve a fizikának?
Ha a matematika ennyire idealizált és ennyire valóságtól független, hogyan lehet mégis ennyire alapvető, érvényes és meghatározó a fizikában?
Minden, ami eddig megállapításra került a matematikával és a fizikával kapcsolatban, igazolja a matematikának a szoros kapcsolatát a fizikával. Azonban minden eddigi megállapítás, bár lényegi dolog, nem mutat rá az alapvető kapcsolatra. Az alapvető kérdés továbbra is fennáll. Az egy meg egy miért kettő a fizikában is? Az egy meg egy miért mindig kettő mindenhol az univerzumban? A matematika mitől nyelve a fizikának? A valóság miért követi a matematika szabályait? Miért használhatók a fizikai mennyiségekre a matematika műveletei és szabályai?
Látszólag van kivétel ez alól a szabály alól. Látszólag lehet találni kivételt a természeti törvényekben, ahol nem érvényes a logikára épülő matematika. Például a sebességek össze adásában. Tudjuk, a speciális relativitáselmélet megmutatta, a valóság pedig igazolta, hogy az, ami az alapvető logika szabályai szerint érvényesnek kellene lennie, a sebességek egyszerű összeadása nem valós művelete a valóságnak. Mintha a valóság nem engedelmeskedne a matematikának. Mintha lenne kivétel a matematika univerzalitása alól. Valójában ebben az esetben sem a matematika érvényessége sérül. A matematika szabályai, műveletei a sebességek összeadására is érvényes, csakhogy a valóság, a valóságunk olyan, hogy a sebességeket nem az összeadás matematikai műveletével lehet összegezni. A sebességek összegzésére egy összetettebb matematikai összefüggés érvényes, amely - hogy a mi valóságunkra specifikus legyen - tartalmaz még egy természeti állandót is. A speciális relativitás elméletének sebességek összeadására vonatkozó matematikai művelete, tehát a matematika érvényes, legalábbis addig, amíg fel nem ismerünk egy még pontosabb összefüggést. A sebességek össze adásában nem a matematika volt pontatlan, hanem a valóság nem a matematika egyszerű összeadás műveletet használja, hanem egy annál bonyolultabb matematikai formulát. A matematikai formula, az abban használt általános matematikai műveletek érvényesek.
A fizika kapcsolata a matematikával nagyon szorosnak kell lennie, hiszen a matematika, az érvényes formája korlátlanul érvényes az adott fizikában. Előfordulhat, hogy időnként át kell írni a fizika matematikai képleteit, de soha nem azért, mert a matematika elvei bizonyulnak hibásnak, hanem azért, mert kiderül, hogy a valóságról alkotott, a tapasztaláson, megfigyelésen alapuló elképzelésünk pontatlan volt. A matematika hibátlan, a valóságról alkotott képünk - amelyre alkalmaztuk a matematikát, hogy leírjuk a szabályait - pontatlan.
Az alapvető kérdés azonban még mindig fennáll. A matematika műveletei miért érvényesek korlátlanul, bárhol, bármikor a fizikai valóságban?
Ahogy az korábban megfogalmazásra került: a matematika azért létezik, azért van struktúrája, azért érvényesek a matematikai műveletek univerzálisan a matematikában, mert:
"A matematika alapját diszkrét, egymástól egyértelműen elválasztott, azonos tulajdonságú elemek alkotják. Bármilyen közel is van két nem azonos szám egymáshoz, azok különböznek egymástól, és ha két szám egyforma, akkor azok minden tulajdonságukban megegyeznek. A műveletek erre az alapra építkezve kapcsolnak össze mennyiségeket, hoznak létre új tulajdonságokat és csoportokat. A műveletek az alapot alkotó mennyiségekre egyformán vonatkoznak. Azonos műveletek azonos eljárásokat jelentenek valamennyi, az alapot alkotó mennyiségre. A matematikai struktúrákat a matematikai műveletek hozzák létre. A struktúrákat a műveletekkel egymáshoz kapcsolt mennyiségek azonos tulajdonságú csoportjai, a létrejövő struktúrák tulajdonságai, ezek egymással kapcsolatban álló viszonyai alkotják."
A matematika azért tudomány, azért működhet, a matematikai műveletek azért érvényesek a matematikán belül univerzálisan, mert a matematika alapját diszkrét, egymástól egyértelműen elválasztott, azonos tulajdonságú elemek alkotják. A fizikai kölcsönhatások megfeleltethetők a matematikai műveleteknek. Tehát abban a valóságban, amelyet diszkrét, egymástól egyértelműen elválasztott, azonos tulajdonságú elemek alkotnak, abban a valóságban, amely ezen alapra épül fel érvényesülhetnek a matematika műveletei. A valóságnak ilyennek kell lennie.
A matematika érvényességének következménye - konklúzió
Mivel a matematika műveletei helytől függetlenül mindenhol működnek a fizikai valóságban, a fizikai valóságunk minden helyszínére igaznak kell lennie ennek az állításnak, hogy a fizikai valóságukat egymástól egyértelműen elválasztott, azonos tulajdonságú elemek alkotják. Az üres térre is. Ahhoz, hogy a matematika általánosan érvényes legyen a fizikai valóságra, az üres tér alapjának is a diszkrét, egymástól egyértelműen elválasztott, azonos tulajdonságú elemeknek kell lennie.
A matematika a nullához végtelenül közeli és egymástól végtelenül kis távolságra lévő mennyiségekkel is tud dolgozni. Ezért is univerzális a matematika. A természet valószínűleg nem ilyen. A valóság nem kedveli a végtelent. A valóságunknak valószínűleg van legkisebb egysége és valószínűleg léteznie kell a legkisebb távolságnak is az egységek között. Ezen korlátok felett a matematika műveletei érvényesülnek az így felépült fizikai valóságban.
A logikát követve, a világunknak - ahol a matematika érvényes - ilyennek kell lennie. De vajon ilyen-e a világunk? A tapasztalat, a megfigyelés támogatja-e ezt a logikai következtetést? A legkisebbel foglalkozó tudomány, a kvantummechanika nem mond ellent ennek. A kvantummechanika már felismerte a legkisebb mennyiséget, ami a Planck állandóhoz köthető és a kvantummechanikában az üres tér sem üres, hanem egy mindenütt jelenlévő kvantumhabként viselkedik.
A legkisebb valóságról alkotott képünk nem mond ellent a matematika és a fizika kapcsolatáról alkotott elméleti következtetésnek. A relativitáselmélet, a nagy mennyiségekkel foglalkozó tudomány azonban kizárta az éter jelenlétét. Az igazság inkább az, hogy a relativitáselmélet nem kizárja az éter létezését, hanem nem látja az éter jelenlétét és nincs szüksége az éter létezésére.
A matematika általános érvényessége azonban sugallja, hogy egy alapstruktúra létezhet a természetben. Az éter, mint alap struktúra létezhet a fizikai valóságban is, csak nem úgy, ahogy azt a relativitás elmélete eredetileg feltételezi.
A GondolHAT következtetése szerint a matematikának ahhoz, hogy általánosan érvényes legyen a maga képére kell alakítania a valóságot és ehhez megteremtenie illetve feltételeznie az üres tér helyett az étert, mint fizikai létezőt. Akkor most melyik tudomány is írja le a valóságot? Mégis a matematika?
A matematika nem természettudomány. Kezdtem kékkel a Penrose könyvének
A matematika a mennyiségekből a műveletek által létrehozott csoportokból és tulajdonságokból struktúrákat hoz létre és ezen struktúrák tulajdonságait vizsgálja.
Ez a meghatározás a geometriára is érvényes, hiszen a geometriát is kezelhetjük mennyiségeken és műveleteken keresztül.
Mi a fizika (és gyakorlatilag valamennyi természettudomány)?
A fizika a valóság, a létező világ, a természet leírása. A fizikán keresztül ismerjük meg a valóság alkotó elemeit, tulajdonságait, egymással való kapcsolatát, kölcsönhatásait. A fizika leírja a való világot, tényeket állapít meg a létező dolgokról, megfigyeli a tulajdonságait. Keresi, meghatározza és leírja a való világ építő elemeit, hogyan hatnak egymásra, hogyan kapcsolódnak egymáshoz, hogyan építenek a kölcsönhatások által struktúrákat.
A fizika alapvetően a valósággal foglalkozik, de a fizikát kiterjeszthetjük a nem tapasztalt valóságra is. Például a fizika foglalkozhat a multiverzummal is, de ebben az esetben is a cél a valóság megismerése. A multiverzumot is azért találjuk ki, mert úgy gondoljuk, hogy az a valóság része.
A fizika foglalkozhat alternatív valósággal is, de ebben az esetben is a fizika a megvalósulható valóságot keresi, a fizika feltételezi, hogy ezek az alternatív valóságok létezhetnek.
Fontos tulajdonsága a valóságnak, hogy a kölcsönhatások által létrejött struktúráknak új, a felépítő elemek által nem hordozott tulajdonságai jöhetnek létre.
A fizika konkrét tudomány, mindig valamilyen létező minőségre, dologra vonatkozik. A fizika nem elvonatkoztatható attól a valóságtól, amit tárgyal.
A matematika univerzális, a fizika specifikus tudomány
Mivel a matematika nem kötődik a dolgok minőségéhez, nem is függ tőle. A matematika bármilyen anyagi minőségen alkalmazható. Természetesen nem minden matematikai művelet értelmezhető és ezért nem minden matematikai művelet használható különböző anyagi minőségekre, de ez nem a matematika korlátja, hanem az anyagi világunk jellemzője.
A fizika alapja és korlátja a megfigyelés, a létező világ. A fizika fejleszthető teoretikusan, akár csupán a matematika eszközeivel is - ilyenkor szoktunk rácsodálkozni a matematika szerepére a természetben -, mégis a legszebb teória, a leglogikusabb következtetés is bizonyulhat hibásnak a fizikában - ahogy az meg is történik sokszor - ha nem felel meg a valóságnak.
A matematika nem minden értelmezhető művelete értelmezhető művelete a valóságnak is. A valóság ezen tulajdonsága biztosítja egyben azt is, hogy a valóság ellentmondás mentes rendszert alkosson. Ha egy elméleti következtetés a fizikában ellentmondásra vezet, akkor az az elméleti út bizonyosan nem lehet érvényes a valóságban.
A matematikai megismerés eszköze az elméleti következtetés, de az ellentmondás mentesség nem zárható ki.
A fizika lényegét tekintve ugyanazt a feladatot végzi, mint a matematika. Mindkettő elemek összességével foglalkozik. A matematika az elemeken matematikai műveleteket végez, a fizika létező kölcsönhatásokat vizsgál. Mindkettő a műveletekkel-kölcsönhatásokkal létrejött új struktúrák tulajdonságaival foglalkozik.
A fizika annyiban több a matematikánál, hogy a minőséggel is foglalkozik, és ugyanezért kevesebb is nála. A fizika annyiban korlátozottabb a matematikánál, hogy a valóság az összes lehetséges lehetőségeknek egy részhalmaza.
Érdekes és fontos jellemzője mindkét tudománynak, hogy mindkettő lezárhatatlan. Mindkét tudományra jellemző, hogy a műveletek-kölcsönhatások során új rendszerek keletkeznek, új tulajdonságokkal. A fizikának az elméleti korlátját a megvalósult valóság végessége határozza meg, a matematikának nincs ilyen korlátja.
Mi a matematika és a fizika kapcsolata?
A matematika a fizikai megismerés eszköze. Mivel a matematika a mennyiségekkel, a valóság minőségétől független jellemzőjével foglalkozik, a matematikai műveletek érvényesek a fizikában.
Fordítva a kijelentés nem érvényes. A fizika nem eszköze a matematika megismerésének. A valós világ korlátozza a matematika érvényességet. Egy valós anyagi rendszerre nem minden matematikai művelet értelmes vagy értelmezhető. A fizika, a valóság korlátozza, hogy melyek azok a matematikai műveletek, amelyek érvényesek az adott anyagi rendszerre.
Alapvető tulajdonsága a fizikának, hogy azok a matematikai műveletek, amelyek az adott fizikai rendszerre érvényesek, univerzálisan érvényesek. Helytől, időtől, és egyéb körülményektől függetlenül működnek. Ezek a fizikai valóságunk szimmetriái. Ezen szimmetriák azért létezhetnek, mert az adott fizikai kölcsönhatások matematikai leírásában szimmetria létezik, érvényes.
A fizika és a matematika kapcsolata egyirányú. A fizika mindig követi a matematika (aktuálisan érvényes) szabályait, de a fizika, a valóság nem meghatározó korlátja a matematikának. A matematika korlátja a tiszta logika (ha egy bizonyítás lépései igazak, akkor a bizonyítás következménye, eredménye is igaz), kiinduló szabályai a nyilvánvaló, vagy absztrakt igazságok (például, ha két mennyiség különböző, akkor azok nem egyformák, vagy ha két egyenes nem találkozik, akkor nincs közös pontjuk).
A valóság megismerésében egy következtetés lépéseinek igazsága a tiszta logikán kívül (mellett, helyett) a megfigyelés pontatlan eszközeire is támaszkodik, az absztrakt igazságok pedig sokszor értelmezhetetlenek a valóságban (két alma különböző is lehet meg azonos is, és a valóságban nem létezik végtelen hosszúságú, de végtelenül vékony struktúra).
A valós világ, a fizika kölcsönhatásokra épül, a kölcsönhatások a valós világ műveletei. A kölcsönhatások szabályozzák a valós világ működését. A fizikai kölcsönhatásoknak specifikus szabályai vannak. Mivel a kölcsönhatások mennyiségeket is jelentenek, a fizikai kölcsönhatások a matematika eszközeivel leírhatok, azonban mivel a kölcsönhatások specifikusak, speciális jellemzőkkel bírnak, csak bizonyos meghatározott matematikai eszközök használhatók, érvényesek. Ezeknek a specialitásoknak a felismerése adja a fizika, mint tudomány célját, a matematika pedig eszközöket biztosít ennek a megismerésnek.
Miért működik a matematika a valóság megismerésében?
Mivel a valóság mennyiségekre épül, a matematika természetszerűleg alkalmazható a világ megismerésében. A valóságban megvalósuló, létező kölcsönhatásoknak a fizikai mennyiségekre vonatkozó specifikuma szabályozza, határozza meg, hogy mely matematikai műveletek alkalmazhatók az adott anyagi rendszerre. Például, a quantum mechanikában szükséges az irracionális számok használata. Miért? Azért, mert a quantum mechanika kölcsönhatásainak rendszere, struktúrája, szimmetriai megfeleltethető az irracionális számok műveleteinek, a matematikai eszközrendszer struktúrájának. A fizika más területein is hasonló megfeleltetések érvényesek.
A fizika fejlődése a megfigyelésen alapszik. Azonban, ha már képesek vagyunk egy közelítő képet alkotni az adott fizikai rendszerről és a kölcsönhatásairól, a fizika fejlődhet teoretikusan is, a logika eszközei segítségével, de minden új következtetés csak akkor tekinthető érvényesnek, ha a valóság, a megfigyelés támogatja, megfelel a következtetésnek.
A matematika mitől a nyelve a fizikának?
Ha a matematika ennyire idealizált és ennyire valóságtól független, hogyan lehet mégis ennyire alapvető, érvényes és meghatározó a fizikában?
Minden, ami eddig megállapításra került a matematikával és a fizikával kapcsolatban, igazolja a matematikának a szoros kapcsolatát a fizikával. Azonban minden eddigi megállapítás, bár lényegi dolog, nem mutat rá az alapvető kapcsolatra. Az alapvető kérdés továbbra is fennáll. Az egy meg egy miért kettő a fizikában is? Az egy meg egy miért mindig kettő mindenhol az univerzumban? A matematika mitől nyelve a fizikának? A valóság miért követi a matematika szabályait? Miért használhatók a fizikai mennyiségekre a matematika műveletei és szabályai?
Látszólag van kivétel ez alól a szabály alól. Látszólag lehet találni kivételt a természeti törvényekben, ahol nem érvényes a logikára épülő matematika. Például a sebességek össze adásában. Tudjuk, a speciális relativitáselmélet megmutatta, a valóság pedig igazolta, hogy az, ami az alapvető logika szabályai szerint érvényesnek kellene lennie, a sebességek egyszerű összeadása nem valós művelete a valóságnak. Mintha a valóság nem engedelmeskedne a matematikának. Mintha lenne kivétel a matematika univerzalitása alól. Valójában ebben az esetben sem a matematika érvényessége sérül. A matematika szabályai, műveletei a sebességek összeadására is érvényes, csakhogy a valóság, a valóságunk olyan, hogy a sebességeket nem az összeadás matematikai műveletével lehet összegezni. A sebességek összegzésére egy összetettebb matematikai összefüggés érvényes, amely - hogy a mi valóságunkra specifikus legyen - tartalmaz még egy természeti állandót is. A speciális relativitás elméletének sebességek összeadására vonatkozó matematikai művelete, tehát a matematika érvényes, legalábbis addig, amíg fel nem ismerünk egy még pontosabb összefüggést. A sebességek össze adásában nem a matematika volt pontatlan, hanem a valóság nem a matematika egyszerű összeadás műveletet használja, hanem egy annál bonyolultabb matematikai formulát. A matematikai formula, az abban használt általános matematikai műveletek érvényesek.
A fizika kapcsolata a matematikával nagyon szorosnak kell lennie, hiszen a matematika, az érvényes formája korlátlanul érvényes az adott fizikában. Előfordulhat, hogy időnként át kell írni a fizika matematikai képleteit, de soha nem azért, mert a matematika elvei bizonyulnak hibásnak, hanem azért, mert kiderül, hogy a valóságról alkotott, a tapasztaláson, megfigyelésen alapuló elképzelésünk pontatlan volt. A matematika hibátlan, a valóságról alkotott képünk - amelyre alkalmaztuk a matematikát, hogy leírjuk a szabályait - pontatlan.
Az alapvető kérdés azonban még mindig fennáll. A matematika műveletei miért érvényesek korlátlanul, bárhol, bármikor a fizikai valóságban?
Ahogy az korábban megfogalmazásra került: a matematika azért létezik, azért van struktúrája, azért érvényesek a matematikai műveletek univerzálisan a matematikában, mert:
"A matematika alapját diszkrét, egymástól egyértelműen elválasztott, azonos tulajdonságú elemek alkotják. Bármilyen közel is van két nem azonos szám egymáshoz, azok különböznek egymástól, és ha két szám egyforma, akkor azok minden tulajdonságukban megegyeznek. A műveletek erre az alapra építkezve kapcsolnak össze mennyiségeket, hoznak létre új tulajdonságokat és csoportokat. A műveletek az alapot alkotó mennyiségekre egyformán vonatkoznak. Azonos műveletek azonos eljárásokat jelentenek valamennyi, az alapot alkotó mennyiségre. A matematikai struktúrákat a matematikai műveletek hozzák létre. A struktúrákat a műveletekkel egymáshoz kapcsolt mennyiségek azonos tulajdonságú csoportjai, a létrejövő struktúrák tulajdonságai, ezek egymással kapcsolatban álló viszonyai alkotják."
A matematika azért tudomány, azért működhet, a matematikai műveletek azért érvényesek a matematikán belül univerzálisan, mert a matematika alapját diszkrét, egymástól egyértelműen elválasztott, azonos tulajdonságú elemek alkotják. A fizikai kölcsönhatások megfeleltethetők a matematikai műveleteknek. Tehát abban a valóságban, amelyet diszkrét, egymástól egyértelműen elválasztott, azonos tulajdonságú elemek alkotnak, abban a valóságban, amely ezen alapra épül fel érvényesülhetnek a matematika műveletei. A valóságnak ilyennek kell lennie.
A matematika érvényességének következménye - konklúzió
Mivel a matematika műveletei helytől függetlenül mindenhol működnek a fizikai valóságban, a fizikai valóságunk minden helyszínére igaznak kell lennie ennek az állításnak, hogy a fizikai valóságukat egymástól egyértelműen elválasztott, azonos tulajdonságú elemek alkotják. Az üres térre is. Ahhoz, hogy a matematika általánosan érvényes legyen a fizikai valóságra, az üres tér alapjának is a diszkrét, egymástól egyértelműen elválasztott, azonos tulajdonságú elemeknek kell lennie.
A matematika a nullához végtelenül közeli és egymástól végtelenül kis távolságra lévő mennyiségekkel is tud dolgozni. Ezért is univerzális a matematika. A természet valószínűleg nem ilyen. A valóság nem kedveli a végtelent. A valóságunknak valószínűleg van legkisebb egysége és valószínűleg léteznie kell a legkisebb távolságnak is az egységek között. Ezen korlátok felett a matematika műveletei érvényesülnek az így felépült fizikai valóságban.
A logikát követve, a világunknak - ahol a matematika érvényes - ilyennek kell lennie. De vajon ilyen-e a világunk? A tapasztalat, a megfigyelés támogatja-e ezt a logikai következtetést? A legkisebbel foglalkozó tudomány, a kvantummechanika nem mond ellent ennek. A kvantummechanika már felismerte a legkisebb mennyiséget, ami a Planck állandóhoz köthető és a kvantummechanikában az üres tér sem üres, hanem egy mindenütt jelenlévő kvantumhabként viselkedik.
A legkisebb valóságról alkotott képünk nem mond ellent a matematika és a fizika kapcsolatáról alkotott elméleti következtetésnek. A relativitáselmélet, a nagy mennyiségekkel foglalkozó tudomány azonban kizárta az éter jelenlétét. Az igazság inkább az, hogy a relativitáselmélet nem kizárja az éter létezését, hanem nem látja az éter jelenlétét és nincs szüksége az éter létezésére.
A matematika általános érvényessége azonban sugallja, hogy egy alapstruktúra létezhet a természetben. Az éter, mint alap struktúra létezhet a fizikai valóságban is, csak nem úgy, ahogy azt a relativitás elmélete eredetileg feltételezi.
A GondolHAT következtetése szerint a matematikának ahhoz, hogy általánosan érvényes legyen a maga képére kell alakítania a valóságot és ehhez megteremtenie illetve feltételeznie az üres tér helyett az étert, mint fizikai létezőt. Akkor most melyik tudomány is írja le a valóságot? Mégis a matematika?
A matematika nem természettudomány. Kezdtem kékkel a Penrose könyvének
Matematikai meglátás
Platonizmus vagy intuicionizmus?
Gödel-típusú tételek Turing eredményéből
Így ha Hilbertnek sikerült volna megtalálnia matematikai rendszerét – axiómák és eljárási szabályok egy rendszerét, amely elég erős, hogy formális bizonyítással eldönthessük a rendszeren belül megfogalmazott, tetszőleges matematikai propozíció igazságát vagy hamisságát – akkor volna általános, algoritmikus módszerünk az ilyen propozíciók igazságának eldöntésére. Miért? Mert ha az előbb vázolt eljárással egy bizonyítás utolsó sorában végül is ráakadunk a keresett propozícióra, akkor bebizonyítottuk ezt a propozíciót. Ha, ellenkezőleg, propozíciónk tagadását találjuk meg mint utolsó sort, akkor megcáfoltuk azt. Ha Hilbert rendszere teljes volna, akkor e két lehetőség egyike mindig bekövetkezne (és ha konzisztens, akkor soha nem következnének be egyszerre). Mechanikus eljárásunk így valamelyik lépésben mindig megszakadna, és univerzális algoritmusunk volna a rendszer minden propozíciója igazságának vagy az ellenkezőjének meghatározására. Ez ellentmondana Turing eredményének, hogy matematikai propozíciók eldöntésére nincs általános algoritmus, amint azt a 2. fejezetben bemutattuk. Következésképpen bebizonyítottuk Gödel tételét, hogy semmilyen, Hilbert által áhított rendszer nem lehet teljes a megtárgyalt értelemben.
El tudjuk-e érni, hogy a Turing-gépek minden szükséges művelete végrehajtható legyen csak aritmetikát használva? Másképpen megfogalmazva: ki lehet-e fejezni a természetes számok minden kiszámítható függvényét (azaz rekurzív vagy algoritmikus függvényeket – a Turing-gép munkájának eredményeit) a közönséges aritmetikával? Majdnem igaz, hogy igen, de nem egészen. Egy extra műveletet hozzá kell csatolnunk az aritmetika és logika megszokott szabályaihoz (amelyek között a ∃ és ∀ már ott van). Ez a művelet egyszerűen kiválasztja
„az x legkisebb természetes számot, amelyre K(x) igaz”, ahol K( ) tetszőlegesen adott, aritmetikailag kiszámítható propozíciós függvény – amelyre feltételeztük, hogy van ilyen szám, azaz hogy ∃ x[K(x)] igaz. (Ha nem volna, akkor műveletünk „örökké futna”,53 próbálná megtalálni a kívánt, de nem létező x-et.) Mindenesetre az említett bizonyítás Turing eredménye alapján megállapítja, hogy Hilbert programja a matematika egész ágainak egy formális rendszeren belül végzett számításokká való redukálására valóban tarthatatlan. ha adott egy tetszőleges algoritmus, amely eldönti, hogy egy Turing-gép megáll-e vagy sem, akkor tudunk csinálni olyan Turing-gépet, amelyről mi látjuk, hogy nem áll meg, de az algoritmus nem. (Emlékezzünk vissza, ragaszkodtunk ahhoz, hogy az algoritmusnak helyesen kell tájékoztatnia bennünket, amikor egy Turing-gép meg fog állni, bár olykor elmulaszthatja megmondani, hogy a Turing-gép nem fog megállni – mert maga is a végtelenségig fut.) Így ugyanúgy, mint az előbb a Gödel-tételnél, most is van egy propozíciónk, amelyről meglátásunk elárulja, hogy igaz kell legyen (hogy a Turing-gép nem áll meg), de az adott algoritmus nem képes ezt megmondani nekünk.
Így ha Hilbertnek sikerült volna megtalálnia matematikai rendszerét – axiómák és eljárási szabályok egy rendszerét, amely elég erős, hogy formális bizonyítással eldönthessük a rendszeren belül megfogalmazott, tetszőleges matematikai propozíció igazságát vagy hamisságát – akkor volna általános, algoritmikus módszerünk az ilyen propozíciók igazságának eldöntésére. Miért? Mert ha az előbb vázolt eljárással egy bizonyítás utolsó sorában végül is ráakadunk a keresett propozícióra, akkor bebizonyítottuk ezt a propozíciót. Ha, ellenkezőleg, propozíciónk tagadását találjuk meg mint utolsó sort, akkor megcáfoltuk azt. Ha Hilbert rendszere teljes volna, akkor e két lehetőség egyike mindig bekövetkezne (és ha konzisztens, akkor soha nem következnének be egyszerre). Mechanikus eljárásunk így valamelyik lépésben mindig megszakadna, és univerzális algoritmusunk volna a rendszer minden propozíciója igazságának vagy az ellenkezőjének meghatározására. Ez ellentmondana Turing eredményének, hogy matematikai propozíciók eldöntésére nincs általános algoritmus, amint azt a 2. fejezetben bemutattuk. Következésképpen bebizonyítottuk Gödel tételét, hogy semmilyen, Hilbert által áhított rendszer nem lehet teljes a megtárgyalt értelemben.
El tudjuk-e érni, hogy a Turing-gépek minden szükséges művelete végrehajtható legyen csak aritmetikát használva? Másképpen megfogalmazva: ki lehet-e fejezni a természetes számok minden kiszámítható függvényét (azaz rekurzív vagy algoritmikus függvényeket – a Turing-gép munkájának eredményeit) a közönséges aritmetikával? Majdnem igaz, hogy igen, de nem egészen. Egy extra műveletet hozzá kell csatolnunk az aritmetika és logika megszokott szabályaihoz (amelyek között a ∃ és ∀ már ott van). Ez a művelet egyszerűen kiválasztja
Rekurzívan felsorolható halmazok
Turing és Gödel eredményeinek alapvető kellékeit leírhatjuk grafikus módon a halmazelmélet nyelvén. Ezáltal megszabadulhatunk a formális rendszerektől, a különleges szimbólumoktól, a lényeges pontok mégis megérthetőek. Csak a 0, 1, 2, 3, 4, … természetes számok (véges vagy végtelen) halmazait tekintjük, ezek gyűjteményeit fogjuk vizsgálni, mint például {4, 5, 8}, {0, 57, 100003), {6}, {0}, {1, 2, 3, 4, … , 9999}, {1, 2, 3, 4, …}, {0, 2, 4, 6, 8, …}, vagy éppen a teljes = {0, 1, 2, 3, 4, …} halmaz, vagy a = { } üres halmaz. Csak kiszámíthatósági kérdésekkel fogunk foglalkozni, nevezetesen: „A természetes számok mely típusú halmazait lehet és melyeket nem lehet algoritmus segítségével előállítani?” Van-e már most olyan halmaz, amely rekurzívan felsorolható, de nem rekurzív? Tartsunk egy pillanatnyi szünetet, hogy megjegyezzük, mit vonna ez maga után. Mivel az ilyen halmaz elemeit elő lehet állítani algoritmussal, módunkban áll eldönteni, hogy egy gyaníthatóan a halmazhoz tartozó elem – és amely, tételezzük fel egy pillanatra, ténylegesen a halmaz eleme – valóban a halmazban van-e. Mindössze annyit kell tennünk, hogy algoritmusunkat végigfuttatjuk a halmaz elemein, amíg végül megtaláljuk a vizsgálandó elemet. Tegyük fel azonban, hogy gyanúsított elemünk ténylegesen nincs a halmazban. Algoritmusunk ebben az esetben semmi jóval nem kecsegtet, mert fut a végtelenségig, soha nem jut döntésre. Ehhez a kiegészítő halmazt előállító algoritmusra volna szükségünk. Ha az megtalálja gyanúsítottunkat, akkor biztosan tudjuk, hogy az elem nincs a halmazban. Mindkét algoritmussal könnyű dolgunk lenne. Egyszerűen váltogatnánk a két algoritmust, és valamelyik elkapná a gyanúsítottat. Ez a kellemes helyzet azonban csak a rekurzív halmazoknál valósul meg. Halmazunk most a feltevés szerint csupán rekurzívan felsorolható, de nem rekurzív: a kiegészítő halmaz előállítására nem létezik algoritmus! Így az a furcsa helyzet áll elő, hogy egy halmazban lévő elemről algoritmikusan eldönthetjük, hogy az valóban a halmazban van-e, de algoritmussal nem tudjuk biztosan eldönteni e kérdést olyan elemekre, amelyek nincsenek a halmazban! Van-e már most olyan halmaz, amely rekurzívan felsorolható, de nem rekurzív? Tartsunk egy pillanatnyi szünetet, hogy megjegyezzük, mit vonna ez maga után. Mivel az ilyen halmaz elemeit elő lehet állítani algoritmussal, módunkban áll eldönteni, hogy egy gyaníthatóan a halmazhoz tartozó elem – és amely, tételezzük fel egy pillanatra, ténylegesen a halmaz eleme – valóban a halmazban van-e. Mindössze annyit kell tennünk, hogy algoritmusunkat végigfuttatjuk a halmaz elemein, amíg végül megtaláljuk a vizsgálandó elemet. Tegyük fel azonban, hogy gyanúsított elemünk ténylegesen nincs a halmazban. Algoritmusunk ebben az esetben semmi jóval nem kecsegtet, mert fut a végtelenségig, soha nem jut döntésre. Ehhez a kiegészítő halmazt előállító algoritmusra volna szükségünk. Ha az megtalálja gyanúsítottunkat, akkor biztosan tudjuk, hogy az elem nincs a halmazban. Mindkét algoritmussal könnyű dolgunk lenne. Egyszerűen váltogatnánk a két algoritmust, és valamelyik elkapná a gyanúsítottat. Ez a kellemes helyzet azonban csak a rekurzív halmazoknál valósul meg. Halmazunk most a feltevés szerint csupán rekurzívan felsorolható, de nem rekurzív: a kiegészítő halmaz előállítására nem létezik algoritmus! Így az a furcsa helyzet áll elő, hogy egy halmazban lévő elemről algoritmikusan eldönthetjük, hogy az valóban a halmazban van-e, de algoritmussal nem tudjuk biztosan eldönteni e kérdést olyan elemekre, amelyek nincsenek a halmazban! „Tn(n) megáll” alakú hamis propozíciók, mint előbb megjegyeztük, nem állíthatók elő algoritmussal. Ezért a hamis propozíciók összességükben nem állíthatók elő algoritmussal, mert tetszőleges ilyen algoritmus egyebek között felsorolná az összes fenti „Tn(n) megáll” hamis propozíciót. Hasonlóképpen az összes igaz propozíció sem állítható elő algoritmussal (mert egy ilyen algoritmus triviálisan módosítható volna, hogy az összes hamis propozíciót állítsa elő: egyszerűen venni kellene minden előállított propozíció tagadását). Mivel így az igaz propozíciók nem rekurzívan felsorolhatók (és a hamisak sem), ezért lényegesen összetettebb és mélyebb elrendezést képeznek, mint a rendszeren belül bizonyítható propozíciók. Ez megint Gödel tételének egy megvilágítása: a matematikai igazság fogalma formális bizonyítással csak részben hozzáférhető.
A 4.1. ábrán egy rekurzív halmazt próbáltam vázlatosan ábrázolni mint egy szép egyszerű határvonalakkal rendelkező tartományt; elképzelhetjük, hogy közvetlenül meg lehet mondani, egy adott pont a halmazhoz tartozik-e vagy sem. A képen minden pont egy természetes számot ábrázol. A kiegészítő halmazt szintén egyszerűnek látszó tartomány ábrázolja. A 4.2. ábrán egy rekurzívan felsorolható, de nem rekurzív halmazt próbáltam ábrázolni, mint egy bonyolult határvonalú halmazt. A határ egyik oldalán lévő halmaz – a rekurzívan felsorolható oldal – az elképzelés szerint egyszerűbbnek látszik, mint a másik halmaz. Az ábrák nagyon vázlatosak, és semmilyen értelemben nem szántam „geometriailag pontosnak” azokat. Így nincs jelentősége annak sem, hogy e képeket sima kétdimenziós síkon ábrázoltam! A 4.3. ábrán azt mutattam be vázlatosan, hogyan fekszenek a P, T és A tartományok az halmazon belül.
Rekurzív-e a Mandelbrot-halmaz?
A nem rekurzív halmazoknak meg kell legyen az a tulajdonságuk, hogy nagyon lényeges módon bonyolultak. Bonyolultságuknak bizonyos értelemben le kell győznie minden rendszerezési kísérletet, különben maga a rendszerezés vezetne megfelelő algoritmikus eljáráshoz. Nem rekurzív halmaznál nincs általános algoritmikus út annak eldöntésére, hogy egy elem (vagy „pont”) a halmazhoz tartozik-e vagy sem. A 3. fejezet elején láttunk egy rendkívül bonyolultan kinéző halmazt, a Mandelbrot-halmazt. Bár a meghatározását adó szabályok meglepően egyszerűek, maga a halmaz nagyon bonyolult szerkezetek végtelen változatosságát mutatja. Lehet, hogy a nem rekurzív halmazok egyike mutatkozott meg halandó szemeink előtt? Ám az Olvasónak hamar eszébe jut majd, hogy a bonyolultságnak ezt a mintapéldányát a modern nagy sebességű elektronikus számítógépek technológiájának varázslata idézte fel szemünk számára láthatóan. Nem az algoritmikus működés megtestesülései-e az elektronikus számítógépek? Valóban, ez biztosan igaz, de nem szabad elfelejtenünk, milyen módon hozza létre a számítógép ezeket a képeket. A számítógép úgy ellenőrzi, hogy az Argand-sík egy pontja – egy c komplex szám – a (feketére színezett) Mandelbrot-halmazhoz vagy a (fehéren hagyott) kiegészítő halmazhoz tartozik-e, hogy elindul a 0-tó1, majd z = 0-ra alkalmazza a z → z2 + c leképezést, így kapja c-t, akkor z = c-re alkalmazva c2 + c-t, majd z = c2 + c-re alkalmazva c4 + 2c3 + c2 + c-t és így tovább. Ha ez a 0, c, c2 + c, c4 + 2c3 + c2+ c, … sorozat korlátos marad, akkor a c-t ábrázoló pontot feketére színezzük, egyébként fehér marad. Hogyan mondja meg a gép, hogy az ilyen sorozat korlátos marad-e vagy sem? Elvileg ismernie kell a sorozat végtelen számú tagját! Ez nem kiszámítható dolog. Szerencsére vannak módok arra, hogy a sorozatnak csak véges tagját ismerve megmondjuk, ha a sorozat nem-korlátossá válik. (Ha eléri az origó középpontú, 1 + sugarú kört, akkor biztos, hogy nem korlátos.)Így bizonyos értelemben a Mandelbrot-halmaz kiegészítője (azaz a fehér tartomány) rekurzívan felsorolható. Ha a c komplex szám a fehér tartományban van, akkor ennek a ténynek kiderítésére van algoritmus. Mi a helyzet magával a Mandelbrot-halmazzal – a fekete tartománnyal? Van-e algoritmus annak biztos megállapítására, hogy egy, a fekete tartományban sejtett pont valóban a fekete tartományban van-e? Erre a kérdésre a válasz jelenleg nem ismert.56 Sok munkatársammal, szakértőkkel konzultáltam, egyikük sem tudott ilyen algoritmusról. Nem találkoztak annak bizonyításával sem, hogy ilyen algoritmus nem létezik. A fekete tartományra, legalábbis úgy látszik, nincs ismert algoritmus. Lehet, hogy a Mandelbrot-halmaz kiegészítő halmaza valóban olyan rekurzívan felsorolható halmaz, amely nem rekurzív!Mielőtt e sejtést tovább nyomoznánk, meg kell beszélnünk bizonyos problémákat, amelyeket eddig elkendőztem. Ezeknek majd jelentőségük lesz későbbi vizsgálatainkban a kiszámíthatóságról a fizikában. Az előzőekben valamennyire pontatlan voltam. A „rekurzívan felsorolható” és „rekurzív” kifejezéseket az Argand-sík pontjainak halmazaira alkalmaztam, azaz komplex számok halmazaira. Ezeket a kifejezéseket szigorúan véve csak a természetes számokra vagy más, megszámlálható halmazokra használhatjuk. A 3. fejezetben láttuk, hogy a valós számok nem megszámlálhatóak, így a komplex számok sem lehetnek azok – mert a valós számok speciális komplex számoknak tekinthetők, nevezetesen olyanoknak, amelyek képzetes része eltűnik. A valóságban pontosan „olyan sok” komplex szám van, mint amennyi valós, nevezetesen „ ”. (A komplex és valós számok között úgy lehet például egy-egy értelmű kapcsolatot létesíteni, hogy vesszük minden komplex szám valós és képzetes részének tizedes kifejtését, és ezekből felváltva véve jegyeket, összefésüljük őket: a 3,6781… + i 512,975… komplex szám például az 50132,6977851… valós számnak felel meg.)E probléma elkerülésének egyik módja az lehetne, ha csak a kiszámítható komplex számokra szorítkoznánk, mert a 3. fejezetben láttuk, hogy a kiszámítható valós számok – és ezért a kiszámítható komplex számok is – valóban megszámlálhatók. Ám van ezzel egy komoly nehézség: nincs általános algoritmus annak eldöntésére, hogy két, megfelelő algoritmusukkal adott, kiszámítható szám egyenlő-e egymással vagy sem! (Különbségüket képezhetjük algoritmikusan, de azt nem tudjuk algoritmikusan eldönteni, hogy e különbség nulla-e vagy sem. Képzeljünk el két algoritmust, amelyek rendre a 0,99999… és 1,00000… jegyeket állítják elő, de soha nem tudhatjuk, hogy a 9-esek vagy a 0-k a végtelenségig folytatódnak-e, azaz a két szám egyenlő, vagy egyszer csak más jegy is megjelenik, és a számok nem egyenlőek.) Így soha nem tudhatjuk, hogy e két szám egyenlő-e. Ennek velejárója, hogy még az olyan egyszerű halmazra, mint az Argand-sík egység-körlemeze (azon pontok halmaza, amelyek távolsága az origótól nem nagyobb egy egységnél, azaz a fekete tartomány a 4.4. ábrán) nem lenne algoritmus annak biztos eldöntésére, hogy egy komplex szám rajta van-e a körlemezen. A probléma nem a tartomány belső pontjainál (nem is a körlemezen kívül lévőknél), hanem pont a körlemez szélén, azaz magán az egységkörön fekvőknél lép fel. Az egységkört a körlemez részének tekintjük. Tegyük fel, hogy van egy algoritmusunk, amely előállítja egy komplex szám valós és képzetes részének jegyeit. Ha gyanítjuk is, hogy e komplex szám ténylegesen az egységkörön fekszik, nem tudunk erről kétséget kizáróan megbizonyosodni. Nincs algoritmus annak eldöntésére, hogy az x2 + y2 kiszámítható szám valóban egyenlő-e 1-gyel vagy sem, lévén ez a feltétele annak, hogy az x + iy kiszámítható komplex szám az egységkörön fekszik-e vagy sem. Világos, hogy nem ez az, amit akarunk. Az egység-körlemeznek bizonyára rekurzívnak kellene számítania! Nincs sok nála egyszerűbb halmaz! A probléma megkerülésének egy módja az volna, hogy a határvonalat figyelmen kívül hagyjuk. A belső vagy a külső rész pontjainál biztosan létezik algoritmus e tény kiderítésére. (Állítsuk elő egyszerűen x2 + y2 jegyeit, egyiket a másik után, és egyszer csak találunk a tizedespont után egy 9-től különböző jegyet a 0,99999…-ben vagy egy 0-tól különböző jegyet az 1,00000…-ban.) Ebben az értelemben az egység-körlemez rekurzív. Matematikailag azonban e nézőpont eléggé veszélyes, mert a bizonyításokban gyakran az a lényeges, mi történik a határokon. Lehet viszont, hogy a fizika számára megfelelő az ilyen szemlélet. Később majd újra meg kell fontolnunk ezt a kérdést.Elfogadhatunk egy másik, rokon nézőpontot, amely egyáltalán nem hivatkozik a kiszámítható komplex számokra. Ahelyett, hogy a kérdéses halmazon belül vagy kívül fekvő komplex számokat próbálnánk felsorolni, olyan algoritmust keresünk, amely adott komplex számra eldönti, hogy a halmazban vagy a halmaz kiegészítőjében fekszik-e. Az „adott” szón azt értem, hogy minden ellenőrzésre kerülő komplex számnál – esetleg valamilyen bűvös úton – megkapjuk a valós és képzetes rész egymás után következő jegyeit, annyit, amennyit csak óhajtunk. Nem követelem meg, hogy e jegyek megismerésére legyen ismert vagy ismeretlen algoritmus. A komplex számok egy halmazát „rekurzívan felsorolhatónak” tekintenénk, ha létezne a következő tulajdonságú algoritmus: amikor csak az elmondott módon megkapná a jegyek ilyen sorozatát, akkor véges számú lépés után akkor és csak akkor mondaná azt, hogy „igen”, ha a komplex szám ténylegesen a halmazban fekszik. Kiderül, hogy ez a nézőpont, akárcsak az előbb javasolt első, „nem vesz tudomást” a határokról. Így ebben az értelemben az egység-körlemez belseje és külseje is rekurzívan felsorolhatónak számítana, míg maga a határvonal nem.Számomra nem egészen világos, hogy e nézőpontok egyike vagy másika az, amire igazán szükségünk van.57 A Mandelbrot-halmazra alkalmazva a „határról nem veszünk tudomást” filozófia sokat elveszthet a halmaz bonyolultságából. E halmaz részben „foltokból” – belső résszel rendelkező tartományokból –, részben „indákból” áll. A legszélsőségesebb bonyodalmak az indáknál látszanak, amelyek a legvadabbul tekereghetnek. Az indák azonban nem fekszenek a halmaz belsejében, így „nem vennénk tudomást róluk”, ha elfogadnánk e két filozófia egyikét. Még így, csak a foltokat tekintve sem világos, hogy a Mandelbrot-halmaz rekurzív-e. A kérdés, úgy látszik, egy a halmazra vonatkozó, nem bizonyított sejtésen nyugszik: olyan-e ez a halmaz, mint amilyet „lokálisan összefüggő”-nek neveznek? Nem szándékozom most magyarázni e kijelentés értelmét vagy fontosságát. Csupán azt kívánom jelezni, hogy ezek nehéz problémák, és a Mandelbrot-halmazzal kapcsolatban olyan kérdéseket vetnek fel, amelyek még megoldatlanok, és amelyek közül egyesek a jelenlegi matematikai kutatások élvonalába tartoznak. Vannak más elfogadható nézőpontok is annak a problémának megkerülésére, hogy a komplex számok nem megszámlálhatóak. Ahelyett, hogy az összes kiszámítható komplex számot tekintenénk, szorítkozhatunk e számok egy megfelelő részhalmazára, amelynek az a tulajdonsága, hogy kiszámítható módon eldönthető, egyenlő-e két eleme vagy sem. Egy egyszerű ilyen részhalmaz a „racionális” komplex számok halmaza, amelyek valós és képzetes része egyaránt racionális. Nem hiszem azonban, hogy sokat mondana a Mandelbrot-halmaz indáiról, lévén e nézőpont nagyon korlátozó. Valamivel kielégítőbb lenne az algebrai számok használata – azoké a komplex számoké, amelyek egész együtthatós algebrai egyenletek megoldásai. Például a 129z7 – 33z5 + 725z4 + 16z3 – 2z – 3 = 0 egyenlet minden megoldása algebrai szám. Az algebrai számok megszámlálhatók és kiszámíthatók, és kiszámítható dolog annak eldöntése, hogy két ilyen szám egyenlő-e. (Kiderül, hogy közülük sok van az egységkörön és a Mandelbrot-halmaz indáin.) A kérdés, ha tetszik, úgy fogalmazható, hogy e számok szerint rekurzív-e a Mandelbrot-halmaz vagy sem.Lehet, hogy az algebrai számok alkalmasak lennének e két most tárgyalt halmaz esetében, de nem oldják meg általánosságban az összes nehézséget. Tekintsük ugyanis az y ≥ ex összefüggéssel meghatározott halmazt (a 4.5. ábra fekete tartományát), ahol x + iy(= z) az Argand-sík pontja. A halmaznak és kiegészítőjének belseje rekurzívan felsorolható bármelyik előbb kifejtett nézőpont szerint, azonban a határ, az y = ex (F. Lindemann 1882-ben bebizonyított nevezetes tétele szerint) csak egyetlen algebrai pontot tartalmaz, nevezetesen a z = i pontot. Ebben az esetben a határ algoritmikus természetének felkutatásában az algebrai számok nem segítenek! Nem lenne nehéz megtalálni a kiszámítható számok egy másik alosztályát, amely kielégítő lenne e speciális esetben, de az emberben megmarad az az erős érzés, hogy a helyes nézőpontot még nem találtuk meg.
Vannak más elfogadható nézőpontok is annak a problémának megkerülésére, hogy a komplex számok nem megszámlálhatóak. Ahelyett, hogy az összes kiszámítható komplex számot tekintenénk, szorítkozhatunk e számok egy megfelelő részhalmazára, amelynek az a tulajdonsága, hogy kiszámítható módon eldönthető, egyenlő-e két eleme vagy sem. Egy egyszerű ilyen részhalmaz a „racionális” komplex számok halmaza, amelyek valós és képzetes része egyaránt racionális. Nem hiszem azonban, hogy sokat mondana a Mandelbrot-halmaz indáiról, lévén e nézőpont nagyon korlátozó. Valamivel kielégítőbb lenne az algebrai számok használata – azoké a komplex számoké, amelyek egész együtthatós algebrai egyenletek megoldásai. Például a 129z7 – 33z5 + 725z4 + 16z3 – 2z – 3 = 0 egyenlet minden megoldása algebrai szám. Az algebrai számok megszámlálhatók és kiszámíthatók, és kiszámítható dolog annak eldöntése, hogy két ilyen szám egyenlő-e. (Kiderül, hogy közülük sok van az egységkörön és a Mandelbrot-halmaz indáin.) A kérdés, ha tetszik, úgy fogalmazható, hogy e számok szerint rekurzív-e a Mandelbrot-halmaz vagy sem.Lehet, hogy az algebrai számok alkalmasak lennének e két most tárgyalt halmaz esetében, de nem oldják meg általánosságban az összes nehézséget. Tekintsük ugyanis az y ≥ ex összefüggéssel meghatározott halmazt (a 4.5. ábra fekete tartományát), ahol x + iy(= z) az Argand-sík pontja. A halmaznak és kiegészítőjének belseje rekurzívan felsorolható bármelyik előbb kifejtett nézőpont szerint, azonban a határ, az y = ex (F. Lindemann 1882-ben bebizonyított nevezetes tétele szerint) csak egyetlen algebrai pontot tartalmaz, nevezetesen a z = i pontot. Ebben az esetben a határ algoritmikus természetének felkutatásában az algebrai számok nem segítenek! Nem lenne nehéz megtalálni a kiszámítható számok egy másik alosztályát, amely kielégítő lenne e speciális esetben, de az emberben megmarad az az erős érzés, hogy a helyes nézőpontot még nem találtuk meg.
 Vannak más elfogadható nézőpontok is annak a problémának megkerülésére, hogy a komplex számok nem megszámlálhatóak. Ahelyett, hogy az összes kiszámítható komplex számot tekintenénk, szorítkozhatunk e számok egy megfelelő részhalmazára, amelynek az a tulajdonsága, hogy kiszámítható módon eldönthető, egyenlő-e két eleme vagy sem. Egy egyszerű ilyen részhalmaz a „racionális” komplex számok halmaza, amelyek valós és képzetes része egyaránt racionális. Nem hiszem azonban, hogy sokat mondana a Mandelbrot-halmaz indáiról, lévén e nézőpont nagyon korlátozó. Valamivel kielégítőbb lenne az algebrai számok használata – azoké a komplex számoké, amelyek egész együtthatós algebrai egyenletek megoldásai. Például a
Vannak más elfogadható nézőpontok is annak a problémának megkerülésére, hogy a komplex számok nem megszámlálhatóak. Ahelyett, hogy az összes kiszámítható komplex számot tekintenénk, szorítkozhatunk e számok egy megfelelő részhalmazára, amelynek az a tulajdonsága, hogy kiszámítható módon eldönthető, egyenlő-e két eleme vagy sem. Egy egyszerű ilyen részhalmaz a „racionális” komplex számok halmaza, amelyek valós és képzetes része egyaránt racionális. Nem hiszem azonban, hogy sokat mondana a Mandelbrot-halmaz indáiról, lévén e nézőpont nagyon korlátozó. Valamivel kielégítőbb lenne az algebrai számok használata – azoké a komplex számoké, amelyek egész együtthatós algebrai egyenletek megoldásai. Például aA nemrekurzív matematika néhány példája
A matematika nagyon sok területén merülnek fel nem rekurzív problémák. Így vizsgálhatjuk az olyan problémák osztályát, amelyekre a válasz vagy „igen”, vagy „nem”, de e két lehetőség közötti választásra nem létezik általános algoritmus. A problémák egyes ilyen osztályai különösen egyszerűnek látszanak. .........a diofantoszi aritmetika, alkotórészeinek elemi természete ellenére, a nemalgoritmikus matematika része!58
Valamivel kevésbé elemi példa a sokaságok topologikus ekvivalenciája. Ezt csak röviden említem, mert elképzelhető, hogy van szerepe a 8. fejezetben vizsgált kérdésekben. Hogy megértsük, mi egy „sokaság”, tekintsünk először egy füzér hurkot, amely egydimenziós sokaság, azután egy zárt felületet, egy kétdimenziós sokaságot. Majd próbáljunk elképzelni egyfajta „felületet”, amelynek három vagy magasabb számú dimenziója lehet. Két sokaság „topologikus ekvivalenciája” azt jelenti, hogy az egyik folytonos módon – vágás vagy ragasztás nélkül – a másikba deformálható. Így egy gömbfelület és egy kocka felszíne topologikusan ekvivalensek, viszont mindkettő topologikusan inekvivalens egy gyűrű vagy egy teáscsésze felületével – az utóbbi kettő egymással topologikusan ekvivalens. Kétdimenziós sokaságoknál van algoritmus annak eldöntésére, hogy közülük kettő topologikusan ekvivalens-e – ez valójában az egyes felületek „fogantyúi” számának megszámlálása. Három dimenzióban a kérdésre válasz az írás időpontjában nem ismeretes, de négy vagy több dimenzióban az ekvivalencia eldöntésére nincs algoritmus. A négydimenziós esetnek feltehetően van jelentősége a fizikában, mert Einstein általános relativitáselmélete szerint a tér és az idő együtt négyes sokaságot képez (lásd 5. fejezet). Geroch és Hartle (1987) azt vetette fel, hogy e nem algoritmikus tulajdonságnak jelentősége lehet a „kvantumgravitációban” (vö. még 8. fejezet). Utolsó nem rekurzív matematikai példaként nézzük az euklideszi sík sokszögekkel való lefedésének kérdését. Adott véges számú különböző alakzat, és azt kérdezzük, le lehet-e fedni kizárólag ezekkel a síkot tökéletesen, rések és átfedések nélkül. Az alakzatok ilyen elrendezését a sík egy parkettázásának nevezik. Jól tudjuk, hogy csak négyzetekkel vagy csak egyenlő oldalú háromszögekkel vagy csak szabályos hatszögekkel (10. fejezet, 10.2. ábra) az ilyen parkettázás lehetséges, de csak szabályos ötszögekkel nem. A sík sokféle más alakzattal parkettázható, mint például a 4.6. ábrákon bemutatott kétféle szabálytalan ötszög bármelyikével. Két alakzattal a parkettázás szebben kidolgozott lehet. A 4.7. ábrán két egyszerű példa látható. Mindezeknek a példáknak megvan az a tulajdonsága, hogy periodikusak; két független irányban pontosan ismétlődnek. Matematikai nyelven azt mondjuk, hogy van egy periódus-paralelogramma – egy paralelogramma, amelyet valahogy megjelölve és a két irányban oldalaival párhuzamosan újra és újra lerakva megkapjuk az adott parkettamintát. Egy példa a 4.8. ábrán látható, a bal oldal periodikus parkettázást mutat egy kürt alakú parkettával, a jobb oldal a kapcsolatot mutatja a periódus-paralelogrammával való periodikus parkettázással.
Talán figyelemre méltó, hogy a matematika egy ilyen nyilvánvalóan „triviális” területe – nevezetesen a sík lefedése egyforma alakzatokkal –, amely majdnem a „gyermekjátékhoz” hasonlít, valójában a nem rekurzív matematika része. E területen sok a nehéz és megoldatlan probléma. Nem tudjuk például azt, van-e egyetlen parkettából álló aperiodikus halmaz.Wang, Berger és Robinson a parkettázási problémában négyszög alapú parkettákat használt. Magam tetszőleges alakú sokszögeket megengedtem; az egyes parketták alakjának kiderítésére szükség volna valamilyen megfelelően kiszámítható módszerre. Egy lehetőség az volna, ha a csúcsokat az Argand-sík pontjaiként adnánk meg, ekkor tökéletesen jól leírhatnánk azokat algebrai számokkal.
Talán figyelemre méltó, hogy a matematika egy ilyen nyilvánvalóan „triviális” területe – nevezetesen a sík lefedése egyforma alakzatokkal –, amely majdnem a „gyermekjátékhoz” hasonlít, valójában a nem rekurzív matematika része. E területen sok a nehéz és megoldatlan probléma. Nem tudjuk például azt, van-e egyetlen parkettából álló aperiodikus halmaz.Wang, Berger és Robinson a parkettázási problémában négyszög alapú parkettákat használt. Magam tetszőleges alakú sokszögeket megengedtem; az egyes parketták alakjának kiderítésére szükség volna valamilyen megfelelően kiszámítható módszerre. Egy lehetőség az volna, ha a csúcsokat az Argand-sík pontjaiként adnánk meg, ekkor tökéletesen jól leírhatnánk azokat algebrai számokkal.
A Mandelbrot-halmaz és a nemrekurzív matematika
Térjünk most vissza a Madelbrot-halmazzal foglalkozó korábbi fejtegetésünkhöz. Az illusztráció kedvéért fel fogom tételezni, hogy valamilyen megfelelő értelemben a halmaz nem rekurzív. Ekkor, mivel kiegészítője rekurzívan felsorolható, ezért a halmaz maga nem lehet olyan. Úgy vélem, hogy a Mandelbrot-halmaz egy pár dologra megtanít bennünket a nem rekurzív halmazok és a nem rekurzív matematika természetét illetően.Térjünk vissza a 3.2. ábrához, amellyel a 3. fejezet elején találkoztunk. Vegyük észre, hogy a halmaz legnagyobb része az a nagy szív alakú tartomány, amelyet a 4.13. ábrán A-val jelöltem. Az alakzat neve kardioid, belsejét úgy lehet matematikailag definiálni, mint az Argand-sík azon c pontjainak halmaza, amelyekre c = z – z2, ahol z olyan komplex szám, amelynek távolsága a kezdőponttól kisebb, mint 1/2. Ez a halmaz a korábban javasolt értelemben biztosan rekurzívan felsorolható: létezik algoritmus, amely a tartomány egy belső pontjára alkalmazva kimutatja, hogy a pont valóban a tartomány belsejében van. A tényleges algoritmus a fenti képletből könnyen megkapható.Tekintsük most a fő kardioidtól közvetlenül balra lévő, korongszerű tartományt (a 4.13. ábrán a B tartományt). Belseje a c = z – 1
pontok halmaza, ahol z távolsága a kezdőponttól kisebb, mint 1/4. E tartomány valóban egy korong belseje – egy egzakt kör belsejében lévő pontok halmaza. Ez a fenti értelemben ismét rekurzívan felsorolható. Mi a helyzet a kardioid többi „szemölcsével”? Nézzük meg közülük a két legnagyobbat. Ezek azok a nagyjából kör alakú foltok, amelyek a 3.2. ábrán közelítőleg a kardioid tetején és alján helyezkednek el, és amelyeket a 4.13. ábrán C1-gyel és C2-vel jelöltem. Ezek pontjai a c3 + 2c2 + (1 – z)c + (1 – z)2 = 0 egyenlettel adhatók meg, ahol z most a kezdőponttól 1/8-nál kisebb távolságra lévő pontokon fut végig. Valójában az egyenlet nem csak ezt a két foltot adja meg, hanem a 3.2. ábrán balra látható „bébi”-kardioidszerű alakzatot is – a 3.1. ábra fő tartományát – amelyet a 4.13. ábrán C3-mal jelöltem. E tartományok (együtt vagy külön-külön) újra rekurzívan felsorolható halmazokat képeznek (a korábban javasolt értelemben) egyszerűen azért, mert a fenti képlet létezik.
Korábbi sugalmazásom ellenére, mely szerint a Mandelbrot-halmaz esetleg nem rekurzív, a legnagyobb területeket már tisztába tudtuk tenni teljesen ........a legáltalánosabb problémákat, amelyekbe sokszor beleütközünk, gyakran tudjuk egyszerű algoritmikus eljárásokkal kezelni – amelyek esetleg már évszázadok óta ismertek. Egyesek azonban kiszöknek a hálóból, és kezelésükhöz kifinomultabb eljárásokra van szükség. Az ilyenek természetesen különösen felkeltik a matematikusok érdeklődését, és még hatékonyabb módszerek kidolgozására ösztönzik őket. Ehhez pedig mélyebb és mélyebb bepillantásokra van szükség a matematika e részének természetébe. Talán így értjük meg a fizikai világot is
Bonyolultságelmélet
Az algoritmusok természetéről, létezéséről és korlátairól most és az előző fejezetekben kifejtett érveim nagyon sok tekintetben „elvi” jellegűek voltak. Egyáltalán nem vizsgáltam annak kérdését, hogy a felmerülő algoritmusoknak várhatóan lesz-e gyakorlati értékük. Még azoknál a problémáknál is, amelyeknél világos, hogy léteznek algoritmusok, és az is, hogy hogyan kell ezeket felépíteni, sok ötletességre és kemény munkára lehet szükség, hogy használhatóvá tegyék ezeket az algoritmusokat. Érdekesebbek azok a problémák, amelyeknél polinomiális idő alatt le lehet írni a választ, sőt még ellenőrizni is lehet helyességét. A problémák (algoritmikusan megoldható részének) fontos osztályát jellemzi ez a tulajdonság. Ezeket NP problémáknak (osztályoknak) nevezik. Pontosabban szólva, ha egy NP-ben lévő problémaosztály egy problémájának van megoldása, akkor az algoritmus megadja ezt a megoldást, és polinomiális idő alatt ellenőrizhető kell legyen, hogy a javasolt megoldás valóban megoldás. Azokban az esetekben, amikor a problémának nincs megoldása, az algoritmus ezt megmondja, de ellenőrizni nem kell – polinomiális időben vagy máshogy –, hogy valóban nincs megoldás.64NP problémák sok összefüggésben felbukkannak mind magán a matematikán belül, mind a gyakorlati világban. Mondok egy egyszerű matematikai példát: azt a problémát, hogyan találjunk egy gráfban olyat, amit „Hamilton-kör”-nek neveznek (meglehetősen ijesztő név egy rendkívül egyszerű dologra). „Gráfon” pontok vagy „csúcsok” véges együttesét értjük, amelyben bizonyos számú pár össze van kötve vonalakkal – ezek a gráf „élei”. (Most nem érdekelnek a geometriai vagy a „távolság”-tulajdonságok, csak az, melyik csúcs melyik csúccsal van összekötve. Így nem számít, hogy a csúcsok egy síkban vannak-e – feltéve, hogy nem törődünk az élek kereszteződéseivel – vagy háromdimenziós térben.) A Hamilton-kör egy zárt út (vagy hurok), amely csak a gráf éleiből áll, és minden csúcson pontosan egyszer megy keresztül. A 4.14. ábrán példaként egy gráf látható, benne egy Hamilton-körrel. A Hamilton-kör probléma annak eldöntése, hogy tetszőlegesen adott gráfban létezik-e Hamilton-kör vagy sem, és amikor létezik, akkor egy ilyen explicit megadása.E probléma valójában nemcsak NP, hanem ún. NP-teljes. Ez azt jelenti, hogy tetszőleges más NP probléma átalakítható ebbe polinomiális idő alatt – így ha valaki elegendően okos lenne, és találna egy algoritmust, amely polinomiális idő alatt megoldja a Hamilton-kör problémát, azaz megmutatná, hogy a probléma valóban P-ben van, akkor ebből következne, hogy minden NP probléma P-ben van! Ebből nagyon fontos dolgok következnének. Egy P-ben lévő problémát általánosan „kezelhetőnek” (azaz „elfogadható idő alatt megoldhatónak”) tekintenek, gyors modern számítógépen, ésszerűen nagy n mellett, míg egy NP-ben lévőt, amely nincs P-ben, „kezelhetetlennek” (azaz bár elvileg megoldhatónak, „gyakorlatilag megoldhatatlannak”) ésszerűen nagy n mellett – függetlenül a számítógépek műveleti sebességében bekövetkezhető, bármilyen jellegű növekedéstől. (Az az idő, amennyit egy nem P-ben lévő NP probléma megoldása ténylegesen igénybe venne, nagy n-re gyorsan felülmúlná a világegyetem életkorát, ami gyakorlati problémánál nem sok reménnyel kecsegtet!) Bármilyen okos algoritmus, amely polinomiális idő alatt megoldja a Hamilton-kör problémát, átalakítható volna olyan algoritmusba, amely polinomiális idő alatt megold tetszőleges más NP problémát!Egy másik, NP-teljes probléma65 „az utazó kereskedő problémája”, amely meglehetősen hasonlít a Hamilton-kör problémához, csak ebben az élekhez számok vannak rendelve, és azt a Hamilton-kört keresi, amelyre a számok összege (a kereskedő által beutazott „távolság”) minimális. Az utazó kereskedő problémájának polinomiális idő alatti megoldása ismét minden más NP probléma polinomiális idő alatti megoldásához vezetne. (Ha ilyen megoldást találnának, az címoldalra kerülő újsághír lenne! Ott vannak ugyanis a titkos kódrendszerek, amelyeket az elmúlt néhány év során vezettek be, és amelyek a nagy egész számok szorzattá bontásának problémájára támaszkodnak, lévén ez egy másik NP probléma. Ha ez megoldható volna polinomiális idő alatt, akkor az ilyen kódokat a nagy teljesítményű, modern számítógépek valószínűleg könnyen megfejtenék, de ha nem, akkor a kódok biztonságban vannak. (Lásd Gardner 1989.)A szakértők között általános az a vélemény, hogy tetszőleges Turing-gépszerű eszközzel lehetetlen polinomiális idő alatt megoldani egy NP-teljes problémát, és következésképp P és NP nem azonos. Nagyon valószínű, hogy e sejtés igaz, de még senkinek sem sikerült bebizonyítania. Ez marad a bonyolultságelmélet legfontosabb megoldatlan problémája.
Bonyolultság és kiszámíthatóság a fizikai dolgokban
A bonyolultságelmélet fontos a könyvünkben található fejtegetések szempontjából, mert egy másik kérdést kínál, valamennyire eltérőt attól, hogy a dolgok algoritmikusak-e vagy sem: nevezetesen azt, hogy vajon azok a dolgok, amelyekről tudjuk, hogy algoritmikusak, hasznos módon algoritmikusak-e. A későbbi fejezetekben kevesebbet kell majd foglalkoznom a bonyolultságelmélet kérdéseivel, többet a kiszámíthatósággal. Hajlok ugyanis azt hinni (bár kétségtelen, hogy teljesen megalapozatlanul), hogy eltérően a kiszámíthatóság alapvető kérdésétől, a bonyolultságelmélet nem játszik központi szerepet a szellemi jelenségekben. Mi több, úgy érzem, hogy az algoritmusok gyakorlatiasságának kérdéseit a bonyolultságelmélet mai állásában alig érinti.Persze tévedhetek is a bonyolultság szerepének megítélésében. Amint azt később majd kifejtem (9. fejezet), a bonyolultságelmélet a valódi fizikai objektumokra jelentősen eltérő lehet attól, amit éppen most tárgyaltunk. Hogy e lehetséges különbség láthatóvá váljék, ahhoz ki kellene használni a kvantummechanikának – az atomok és molekulák viselkedése és sok más, esetleg sokkal nagyobb skálán is fontos jelenség e titokzatos, mégis hatékony és pontos elméletének – mágikus tulajdonságait. Ezzel az elmélettel a 6. fejezetben fogunk megismerkedni. A David Deutsch (1985) által felvetett legújabb elképzelések szerint elvileg lehetséges „kvantumszámítógépet” készíteni, amely polinomiális idő alatt megoldhat nem P-ben lévő problémákat. Jelenleg egyáltalán nem világos, hogyan kell olyan valódi fizikai eszközt készíteni, amely (megbízhatóan) úgy viselkedik, mint egy kvantumszámítógép – és ráadásul az eddig számításba vett problémaosztály határozottan mesterséges –, ám az elméleti lehetőség, hogy egy kvantumfizikai eszköz képes lehet tökéletesíteni egy Turing-gépet, úgy látszik, az asztalunkon van.Lehetséges-e, hogy az emberi agy, amelyet e tárgyalásban „fizikai eszköznek” tekintek, noha meghökkentően finom tervezésűnek és bonyolultnak tartom, kihasználja a kvantumelmélet varázslatait? Értjük-e a módját, hogyan lehet a kvantumos jelenségeket előnyösen felhasználni problémák megoldásában vagy ítéletek kialakításában? Elképzelhető-e, hogy még a mai kvantumelméletnél is „mélyebbre” kell mennünk, hogy e lehetséges előnyöket kiaknázzuk? Reális-e az a lehetőség, hogy valóságos fizikai eszközök tökéletesíthetik a Turing-gépek bonyolultságelméletét? És mit mond a kiszámíthatóság elmélete ezekre az eszközökre?
Ez a fenti bekezdés az ahonnan még sokkal érdekesebbé vált számomra az utazás.
Lehetséges-e, hogy az emberi agy, amelyet e tárgyalásban „fizikai eszköznek” tekintek, noha meghökkentően finom tervezésűnek és bonyolultnak tartom, kihasználja a kvantumelmélet varázslatait?
-kérdi Penrose.
Hogy e kérdésekkel foglalkozhassunk, el kell hagynunk a tiszta matematikát, és a következő fejezetekben azt kell megvizsgálnunk, hogyan viselkedik a fizika világ!
és azt igéri átvisz egy másik világba, a nem elvontba...
A bonyolultságelmélet fontos a könyvünkben található fejtegetések szempontjából, mert egy másik kérdést kínál, valamennyire eltérőt attól, hogy a dolgok algoritmikusak-e vagy sem: nevezetesen azt, hogy vajon azok a dolgok, amelyekről tudjuk, hogy algoritmikusak, hasznos módon algoritmikusak-e. A későbbi fejezetekben kevesebbet kell majd foglalkoznom a bonyolultságelmélet kérdéseivel, többet a kiszámíthatósággal. Hajlok ugyanis azt hinni (bár kétségtelen, hogy teljesen megalapozatlanul), hogy eltérően a kiszámíthatóság alapvető kérdésétől, a bonyolultságelmélet nem játszik központi szerepet a szellemi jelenségekben. Mi több, úgy érzem, hogy az algoritmusok gyakorlatiasságának kérdéseit a bonyolultságelmélet mai állásában alig érinti.Persze tévedhetek is a bonyolultság szerepének megítélésében. Amint azt később majd kifejtem (9. fejezet), a bonyolultságelmélet a valódi fizikai objektumokra jelentősen eltérő lehet attól, amit éppen most tárgyaltunk. Hogy e lehetséges különbség láthatóvá váljék, ahhoz ki kellene használni a kvantummechanikának – az atomok és molekulák viselkedése és sok más, esetleg sokkal nagyobb skálán is fontos jelenség e titokzatos, mégis hatékony és pontos elméletének – mágikus tulajdonságait. Ezzel az elmélettel a 6. fejezetben fogunk megismerkedni. A David Deutsch (1985) által felvetett legújabb elképzelések szerint elvileg lehetséges „kvantumszámítógépet” készíteni, amely polinomiális idő alatt megoldhat nem P-ben lévő problémákat. Jelenleg egyáltalán nem világos, hogyan kell olyan valódi fizikai eszközt készíteni, amely (megbízhatóan) úgy viselkedik, mint egy kvantumszámítógép – és ráadásul az eddig számításba vett problémaosztály határozottan mesterséges –, ám az elméleti lehetőség, hogy egy kvantumfizikai eszköz képes lehet tökéletesíteni egy Turing-gépet, úgy látszik, az asztalunkon van.Lehetséges-e, hogy az emberi agy, amelyet e tárgyalásban „fizikai eszköznek” tekintek, noha meghökkentően finom tervezésűnek és bonyolultnak tartom, kihasználja a kvantumelmélet varázslatait? Értjük-e a módját, hogyan lehet a kvantumos jelenségeket előnyösen felhasználni problémák megoldásában vagy ítéletek kialakításában? Elképzelhető-e, hogy még a mai kvantumelméletnél is „mélyebbre” kell mennünk, hogy e lehetséges előnyöket kiaknázzuk? Reális-e az a lehetőség, hogy valóságos fizikai eszközök tökéletesíthetik a Turing-gépek bonyolultságelméletét? És mit mond a kiszámíthatóság elmélete ezekre az eszközökre?
Ez a fenti bekezdés az ahonnan még sokkal érdekesebbé vált számomra az utazás.
Lehetséges-e, hogy az emberi agy, amelyet e tárgyalásban „fizikai eszköznek” tekintek, noha meghökkentően finom tervezésűnek és bonyolultnak tartom, kihasználja a kvantumelmélet varázslatait?
-kérdi Penrose.
Hogy e kérdésekkel foglalkozhassunk, el kell hagynunk a tiszta matematikát, és a következő fejezetekben azt kell megvizsgálnunk, hogyan viselkedik a fizika világ!
és azt igéri átvisz egy másik világba, a nem elvontba...
5. A klasszikus világ
A fizikai elmélet helyzete
Mit kell tudnunk a Természet működéséről, hogy megállapíthassuk, hogyan lehet része a tudatosság? Számít-e igazán, milyen törvények kormányozzák a testeket és agyakat összetevő elemeket? Ha tudatos érzékelésünk csupán algoritmusok lejátszása, ahogy azt sok MI-párti elhitetné velünk, akkor nincs komoly jelentősége annak, hogy ténylegesen mik is ezek a törvények. Minden eszköz, amely képes végrehajtani egy algoritmust, éppen olyan jó volna, mint bármelyik másik. Másrészt tudatosságérzésünk esetleg több, mint a puszta algoritmusok összessége. Talán valóban fontosak felépítésünk részletei, mint ahogy fontosak azok a pontos fizikai törvények, amelyek az anyagot kormányozzák, amelyből vagyunk. Talán meg kell értenünk, mi az a mély minőség, amely az anyag igazi természete mögött rejtőzik, és meghatározza a módot, amely szerint minden anyagnak viselkednie kell. A fizika még nincs ezen a ponton. Még sok a megfejtésre váró titok, még sok mély meglátásra van szükség. A legtöbb fizikus és fiziológus mégis úgy ítélné meg a helyzetet, hogy már eleget tudunk azokról a fizikai törvényekről, amelyek lényegesek az olyan normál méretű objektumok működésében, mint az emberi agy. Noha kétségtelen, hogy az agy mint fizikai rendszer kivételesen bonyolult, és részletes szerkezetéről, lényegi működéséről még rengeteget nem tudunk, mégis kevesen állítanák, hogy a viselkedése alapját képező fizikai elvekről bármi lényegeset ne értenénk.Később majd megemlítek egy, a szokásostól eltérő esetet annak bizonyítására, hogy ellenkezőleg, még nem értjük elég jól a fizikát ahhoz, hogy segítségével agyunk működését, akár csak elvileg is, megfelelően leírhassuk. Ehhez szükség lesz arra, hogy először némi áttekintést adjak a fizika jelenlegi állásáról. E fejezet azzal foglalkozik, amit „klasszikus fizikának” hívnak, amely magában foglalja mind Newton mechanikáját, mind Einstein relativitáselméletét. A „klasszikus” szó itt lényegében azokat az elméleteket jelenti, amelyek a kvantumelmélet megjelenése előtt uralkodtak. Utóbbi nagyjából 1925-re tehető (olyan fizikusok ihletett munkáin keresztül, mint Planck, Einstein, Bohr, Heisenberg, Schrödinger, de Broglie, Born, Jordan, Pauli és Dirac). A kvantumelmélet a határozatlanság, indeterminizmus és titokzatosság elmélete, a molekulák, atomok és szubatomi részecskék viselkedését írja le. A klasszikus elmélet viszont determinisztikus, benne a múlt mindig meghatározza a jövőt. A klasszikus fizikában még így is sok a titokzatos dolog, annak ellenére, hogy a századok során összegyűjtött tudás egészen fantasztikusan pontos képhez juttatott bennünket. Meg kell majd vizsgálnunk a kvantumelméletet is (6. fejezet), mert ellentétben azzal, ami a fiziológusok körében a többségi nézetnek látszik, úgy hiszem, hogy a kvantumos jelenségek valószínűleg fontosak az agy működésében – de ez a következő fejezetek tárgya lesz.Drámainak mondható, amit a tudomány napjainkig elért. Csak körül kell néznünk, hogy tanúsítsuk, milyen rendkívüli erőhöz jutottunk a Természet megértése által. A modern világ technológiája jelentős mértékben az empirikus tapasztalatok nagy gazdagságából származik. Ám a fizikai elmélet az, ami meghatározó módon technológiánk alapjául szolgál, és a fizikai elmélet az, ami most bennünket érdekel. A rendelkezésünkre álló elméletek pontossága igen figyelemreméltó. Ám nem csupán pontosságuk az erősségük, hanem az a körülmény is, hogy pontos és részletes matematikával rendkívül jól kezelhetőnek és ellenőrizhetőnek bizonyultak. Ezek együttesen nyújtanak számunkra egy valóban meggyőző erejű tudományt.E fizikai elmélet jó része nem különösebben új. Ha egy esemény kiemelhető az összes többi elé, akkor az Isaac Newton Principiájának 1687-es megjelentetése. Ez a nagy jelentőségű mű megmutatta, hogyan lehet néhány alapvető fizikai elv alapján megérteni és gyakran meglepő pontossággal megjósolni a fizikai objektumok viselkedésének nagy részét. (A Principia figyelemre méltó fejlődést hozott a matematikai technikában is, bár több gyakorlati módszert később dolgoztak ki Euler és mások.) Newton munkája, amint ő készségesen elismerte, sokban támaszkodott a korábbi gondolkodók eredményeire, akik közül kimagaslik Galileo Galilei, René Descartes és Johannes Kepler. Fontos, alapvető fogalmak még régebbi gondolkodóktól származtak, ilyenek például Platón, Eudoxosz, Eukleidész, Arkhimédész és Appolóniosz geometriai elképzelései. Később majd többet kell ezekről mondanom.Az eltérések Newton dinamikájának alapsémájától később jelentek meg, először James Clerk Maxwellnek a tizenkilencedik század közepén kidolgozott elektromágneses elmélete. Ez nemcsak az elektromos és mágneses mezők klasszikus viselkedésével foglalkozott, hanem a fényével is!66 A fejezet későbbi részében erre a nevezetes elméletre fordítjuk figyelmünket. Maxwell elmélete igen fontos a mai technológia szempontjából, és az is kétségtelen, hogy az elektromágneses jelenségek hozzátartoznak agyunk működéséhez. Kevésbé világos azonban az, hogy lehet-e valami jelentősége gondolkodási folyamatunkban a két nagy relativitáselméletnek, amelyek Albert Einstein nevéhez fűződnek. A speciális relativitáselmélet a Maxwell-egyenletek vizsgálatából fejlődött ki, Henri Poincaré, Hendrick Antoon Lorentz és Einstein alkották meg (később Hermann Minkowski adott elegáns geometriai leírást) abból a célból, hogy megmagyarázzák a testek rejtélyes viselkedését, amikor azok a fénysebességhez közeli sebességgel mozognak. Einstein híres egyenlete, az „E = mc2”, része az elméletnek. Azonban az elmélet hatása a technológiára mindeddig nagyon csekélynek bizonyult (kivéve, amikor a magfizikába szólt bele), és jelentősége agyunk működésében a legjobb esetben is csak periferiálisnak látszik. A speciális relativitáselmélet viszont mond valami mélyet a fizikai valóságról az idő természetével kapcsolatban. A következő fejezetekben látni fogjuk, hogy ez bizonyos rejtett problémákhoz vezet a kvantumelméletben, aminek jelentősége lehet azzal kapcsolatban, ahogy az „idő múlását” érzékeljük. Továbbmenve, először meg kell értenünk a speciális elméletet, csak utána tudjuk megfelelően értékelni Einstein általános relativitáselméletét – azt az elméletet, amely görbült téridő segítségével írja le a gravitációt. Ennek az elméletnek a technológiára eddig majdnem semmi hatása nem volt,67 és szélsőségesen különösnek látszana bármi jelentőséget tulajdonítani neki agyunk működésében! De érdekes módon éppen az általános relativitáselméletnek lesz a legnagyobb a jelentősége későbbi megfontolásainkban, kivált a 7. és 8. fejezetben, ahol térben és időben a legnagyobb távolságokig kell majd elmennünk, hogy megragadjunk valamit a változásokból, amelyekre szerintem szükség van ahhoz, hogy a kvantumelméletről megfelelően koherens képünk alakuljon ki – de erről többet majd később!Ezek a klasszikus fizika nagy területei. Mi a helyzet a kvantumfizikával? Ellentétben a relativitáselmélettel, a kvantumelmélet igazán jelentős hatást kezd kifejteni a technológiára. Ez részben azoknak a felismeréseknek a következménye, amelyeket a kvantumelmélet nyújtott bizonyos technológiailag fontos területeken, mint a kémia és a fémkohászat. Egyesek már azt mondják, hogy ezek a területek tulajdonképpen beolvadtak a fizikába, annak a sok új felismerésnek következtében, amelyeket a kvantumelmélet adott nekünk. Vannak ráadásul egészen új jelenségek, amelyekkel szintén a kvantumelmélet ajándékozott meg, a legismertebb ezek között, azt hiszem, a lézer. Nem lehetséges-e, hogy a kvantumelmélet egyes lényeges pontjai döntő szerepet játszanak abban a fizikában is, amely gondolati folyamataink alapjait képezi?Mi a helyzet a legújabb fizikai felismerésekkel? Egyes olvasók már találkozhattak az olyan izgalmasan kifejezett elképzelésekkel, mint a „kvarkok”, a „GUT” (Grand Unified Theories = nagy egyesített elméletek), az „inflatorikus világegyetem” (lásd a 153. jegyzetet), a „szuperszimmetria”, a „(szuper)húr-elmélet” stb. Hogy néznek ki ezek az új elméletek összehasonlítva azokkal, amelyekre éppen az előbb utaltam? Kell-e tudnunk ezekről is? Azt hiszem, a dolgokat a megfelelő megvilágításba helyezendő, fel kell állítanom az alapvető fizikai elméletek három széles osztályát. Ezekre a következő címkéket akasztom: - SZUPER,
- HASZNOS,
- KÍSÉRLETI.
A SZUPER kategóriába kell tartozzék mindaz, amiről az előző bekezdésekben szó volt. A SZUPER minősítéshez nem tartom fontosnak, hogy az elmélet ellenpélda nélkül alkalmazható legyen a világ jelenségeire, de megkövetelem, hogy olyan tartományban és olyan pontossággal legyen alkalmazható, amely valamilyen értelemben rendkívüli. Ahhoz képest, hogy milyen feltételekhez kötöm a SZUPER minősítést, igazán figyelemre méltó, hogy ebben az osztályban van egyáltalán elmélet! Nincs tudomásom semmilyen más tudomány semmilyen más alapelméletéről, amely jogosan bekerülhetne ebbe az osztályba. Talán a természetes kiválasztódás Darwin és Wallace által javasolt elmélete áll hozzá a legközelebb, de azért még eléggé távol.A SZUPER elméletek legrégebbije az euklideszi geometria, amelyről valamennyit tanultunk az iskolában. A régiek egyáltalán nem tekinthették fizikai elméletnek, pedig valójában az: nagyszerű és nagyon pontos elmélete a fizikai térnek – és a merev testek geometriájának. Miért tekintem inkább fizikai elméletnek, mintsem a matematika egyik ágának? Ironikusan mondhatnánk: amiért e nézetet valljuk, annak egyik legtisztább oka az, hogy ma már tudjuk, az euklideszi geometria mint az életterünkként szolgáló fizikai tér leírása nem teljesen pontos! Einstein általános relativitáselmélete azt mondja nekünk, hogy a tér(idő) gravitációs mező jelenléte esetén „görbült” (azaz nem teljesen euklideszi). Ám ez a tény nem változtatja meg az euklideszi geometria SZUPER jellegét. Méteres tartományban az euklideszi simaságtól való eltérés igazán parányi, a geometria euklideszi módon való kezelésének hibája kisebb, mint egy hidrogénatom átmérője!Jogosan mondhatjuk, hogy a statika elmélete (amely a nyugalomban lévő testekkel foglalkozik), ahogy Arkhimédész, Papposz és Stevin szép tudománnyá fejlesztették, szintén SZUPER-nek minősíthető. Ez az elmélet mára beolvadt a newtoni mechanikába. A dinamikának (a mozgó testek tudományának) a Galilei által 1600 körül bevezetett és Newton által pompás, átfogó elméletté fejlesztett, mély ideái kétségtelenül a SZUPER osztályba kell kerüljenek. A bolygók és holdak mozgására alkalmazva az elmélet megfigyelt pontossága tüneményes – jobb, mint egy a tízmillióhoz. Ugyanaz a newtoni rendszer hasonló pontossággal alkalmazható itt a Földön – és kint a csillagok és galaxisok között. Maxwell elmélete hasonlóképpen rendkívül nagy tartományban érvényes pontosan, az atomok és szubatomi részecskék piciny skálájától kifelé a galaxisok néhány milliószor milliószor milliószor milliószor milliószor milliószor nagyobb skálájáig! (A tartomány kisméretű végén a Maxwell-egyenleteket a kvantummechanika szabályaival kell megfelelően kombinálni.) Ez is bizonnyal kiérdemli a SZUPER minősítést.Einstein speciális relativitáselmélete (melynek előzményei már Poincarénál is fellelhetők, és amit Minkowski elegánsan újrafogalmazott) csodálatosan pontos leírását adja azoknak a jelenségeknek, amelyekben a tárgyak sebessége megközelítheti a fénysebességet – ahol Newton leírása végül botladozni kezd. Einstein legcsodálatosabb és legeredetibb általános relativitáselmélete általánosítja Newton dinamikai (gravitáció-) elméletét, és örökölve annak a bolygók és holdak mozgásának leírásában mutatott minden pontosságát, még meg is javítja azt. Ráadásul megmagyaráz egy sor részletes megfigyelést, amelyek a régi newtoni rendszerrel nem egyeztethetők össze. Ezek egyike (a „kettős pulzár”) azt mutatja, hogy Einstein elméletének pontossága nagyjából 1 a 1014-hez. Mindkét relativitáselméletet – a második magába olvasztja az elsőt – a SZUPER osztályba kell sorolnunk (matematikai eleganciájukért majdnem annyira, mint pontosságukért).A kvantummechanika különösképpen szép és forradalmi elméletével magyarázott jelenségek tartománya, és a pontosság, ahogy a kísérletekkel megegyezik, világosan mondja nekünk, hogy a kvantumelméletet is biztosan SZUPER-nak kell minősítenünk. Az elméletnek ellentmondó megfigyelést nem ismerünk – erejét elsősorban mégsem ez adja, hanem az a számos, mindeddig megmagyarázhatatlan jelenség, amelyet az elmélet most megmagyaráz. A kémia törvényei, az atomok stabilitása, a színképvonalak élessége (vö. 6. fejezet) és megfigyelt, nagyon különös szerkezetük, a szupravezetés (nulla elektromos ellenállás) furcsa jelensége és a lézerek viselkedése csak néhány ezek közül.A SZUPER osztályba kerüléshez magas követelményeket állítok, de ez az, amihez a fizikában hozzászoktunk. Mi a helyzet az újabb elméletekkel? Véleményem szerint csak egy olyan van, amely SZUPER-nek minősíthető, és ez nem is nagyon új: a kvantumelektrodinamika (vagy QED) nevet viselő elmélet, amelyet Jordan, Heisenberg és Pauli munkássága alapozott meg, Dirac fogalmazott meg 1926 és 1934 között, és Bethe, Feynman, Schwinger és Tomonaga tett működőképessé 1947 – 48-ban. Ez az elmélet a kvantummechanika elvei és a speciális relativitás kombinációjaként jött létre, beépítve magába a Maxwell-egyenleteket és egy, Diractól származó, az elektronok mozgását és spinjét szabályozó alapegyenletet. Az elmélet egészében véve nem rendelkezik a korábbi SZUPER elméletek kényszerítő eleganciájával vagy következetességével, de valóban tüneményes pontossága alapján ebbe az osztályba sorolható. Egyik különösen nevezetes eredménye az elektron mágneses momentumának értéke. (Az elektronok a pörgő elektromos töltések pici mágneseihez hasonlóan viselkednek. A mágneses momentum kifejezés e piciny mágnes erősségére vonatkozik.) A QED-ből erre az 1,001 159 652 46 érték jön ki (megfelelő egységekben – az utolsó két jegyben kb. 20 megengedett hibával), míg a legújabb kísérleti érték 1,001 159 652 193 (a lehetséges hiba kb. 10 az utolsó két jegyben). Az ilyen fokú pontosság, amint arra Feynman rámutatott, a New York és Los Angeles közötti távolságot egy emberi hajszál szélességénél kisebb megengedett eltéréssel határozná meg! Az elmélet ismeretére nem lesz szükségünk, de a teljesség kedvéért néhány lényeges vonását a következő fejezet végén vázlatosan megemlítem.68Vannak olyan forgalomban lévő elméletek, amelyeket a HASZNOS osztályba sorolok. Kettőre ezek közül nem lesz szükségünk, de a megemlítést megérdemlik. Az egyik a hadronoknak nevezett szubatomi részecskék (az atommagot felépítő protonok, neutronok, mezonok stb. – vagy pontosabban az erősen kölcsönható részecskék) Gell-Mann–Zweig-féle kvarkmodellje és e részecskék kölcsönhatásainak (később kidolgozott) részletes elmélete, amely kvantumszín-dinamika vagy QCD néven ismert. Az elképzelés az, hogy minden hadron kvarkoknak nevezett összetevőkből épül fel, amelyek egymással a Maxwell-elmélet egy bizonyos általánosítása (az ún. „Yang–Mills-elmélet”) szerint hatnak kölcsön. A másik egy olyan (Glashow, Salam, Ward és Weinberg által kidolgozott – és újra a Yang–Mills-elméletet használó) elmélet, amely az elektromágneses erőket a radioaktív bomlásokért felelős „gyenge” kölcsönhatásokkal házasítja össze. Ez az elmélet tartalmazza az ún. leptonok (elektronok, müonok, neutrinók, W- és Z-részecskék – a „gyengén kölcsönható” részecskék) leírását. Mindkét elméletnek vannak jó kísérleti bizonyítékai. Ám különböző okokból sokkal rendetlenebbek, mint azt szeretnénk (a QED is ilyen, de ezek még inkább), és megfigyelt pontosságuk és jósoló erejük messze nem éri el azt a mértéket, ami a SZUPER osztályba soroláshoz szükséges volna. E két elméletet együttesen (a másodikba beleértve a QED-t) gyakran emlegetik standard modellként.Végül van egy más típusú elmélet, amely, én azt hiszem, legalábbis a HASZNOS osztályba tartozik. Ez a világegyetem eredetének elmélete, amelyet ősrobbanás-elméletnek (Nagy Bummnak) neveznek.69 Ez az elmélet fontos szerepet kap majd a 7. és 8. fejezet fejtegetéseiben.Nem gondolom azt, hogy semmi más nem kerülhet a HASZNOS osztályba.70 Van sok már régebben (vagy legújabban) közkedvelt elképzelés. Mondok néhány nevet: „Kaluza–Klein-elméletek”, „szuperszimmetria” (vagy „szupergravitáció”) és a „GUT”-elméletekhez (és bizonyos belőlük származtatott elképzelésekhez, például az „inflatorikus forgatókönyvhöz”, vö. 153. jegyzet) csatlakozó, rendkívül divatos „húr” (vagy „szuperhúr”) elméletek. Véleményem szerint mindezek határozottan a KÍSÉRLETI osztályban vannak. (Lásd Barrow 1988, Close 1983, Davies és Brown 1988, Squires 1985.) A HASZNOS és KÍSÉRLETI osztályok közötti lényeges különbség a jelentős kísérleti megalapozás hiánya az utóbbiba tartozó elméleteknél.71 Nem mondom ezzel azt, hogy némelyikük esetleg nem emelkedhet fel drámaian a HASZNOS, sőt a SZUPER osztályba. Egyesek valóban ígéretes, eredeti elképzeléseket tartalmaznak, de kísérleti alátámasztás nélkül ezek csak elképzelések maradnak. A KÍSÉRLETI osztály nagyon széles. Az itt fellelhető egyes elképzelések bőven tartalmazhatják a megértés lényeges előrehaladásának csíráit, míg mások szembeötlően félresikerültek, mesterkéltek. (Szándékomban állt egy negyediket lehasítani a tiszteletre méltó KÍSÉRLETI osztályból, és mondjuk a FÉLRESIKERÜLT címkével ellátni – de azután meggondoltam magam, mert nem akartam elveszíteni barátaim felét!)Nem kell meglepődnünk azon, hogy a fő SZUPER elméletek régiek. A történelem során biztosan sokkal-sokkal több elmélet volt, amely a KÍSÉRLETI osztályba került volna, de a legtöbbjük sorsa a feledés lett. Hasonlóképpen a HASZNOS osztályban is sok kellett legyen, amelyek azóta eltűntek; de vannak olyanok is, amelyek beolvadtak másokba, amelyek később SZUPER-rá váltak. Nézzünk néhány példát. Mielőtt Kopernikusz, Kepler és Newton sokkal jobb rendszerüket megalkották, volt a bolygómozgásnak egy csodálatosan kidolgozott elmélete, amelyet a régi görögök gondoltak ki, és a ptolemaioszi rendszer néven volt ismert. E rendszer szerint a bolygók mozgása körmozgások bonyolult összegződése révén alakul ki. Egész jól lehetett vele jóslatokat gyártani, de amint nagyobb pontosságra volt szükség, úgy vált egyre bonyolultabbá. Ma a ptolemaioszi rendszer nagyon mesterkéltnek látszik. Jó példája volt ez a HASZNOS elméletnek (vagy húsz évszázaddal ezelőtt!), amely mint fizikai elmélet később teljesen eltűnt, bár tudománytörténeti szerepe vitathatatlan. A végül sikeres HASZNOS elméleteknek az előbbi helyett jó példája Kepler ragyogó elgondolása a bolygók elliptikus mozgásáról. Egy másik példa a kémiai elemek Mengyelejev-féle periódusos rendszere. Önmagukban ezek nem rendelkeztek a megkövetelt „rendkívüli” jósoló erővel, de a későbbiekben „helyes” következtetésekké váltak azokon a SZUPER elméleteken belül, amelyek belőlük nőttek ki (a newtoni dinamika és a kvantumelmélet).Az elkövetkező szakaszokban és fejezetekben nem kell majd sokat mondanom a forgalomban lévő, csupán HASZNOS vagy KÍSÉRLETI elméletekről.
Elég, ha azokról beszélünk, amelyek SZUPER-ek. Valóban szerencsés dolog, hogy vannak ilyen elméleteink, és hogy ilyen figyelemreméltó teljességgel meg tudjuk érteni a világot, amelyben élünk. Végül meg kell próbálnunk majd eldönteni, elég gazdagok-e ezek az elméletek, hogy kormányozzák agyunk és értelmünk működését. A megfelelő helyen erre a kérdésre majd visszatérek; most azonban nézzük meg a SZUPER elméleteket mai formájukban, és próbáljunk eltöprengeni, milyen jelentőségük lehet céljaink szempontjából.
- SZUPER,
- HASZNOS,
- KÍSÉRLETI.
Euklideszi geometria
Az euklideszi geometria az a tárgykör, amelyet az iskolában „geometria” néven tanulunk. Azt hiszem azonban, hogy a legtöbb ember inkább matematikának gondolja, mintsem fizikai elméletnek. Matematika is természetesen, de semmi esetre sem az egyetlen elképzelhető matematikai geometria. E speciális geometria, amelyet Eukleidész hagyott ránk, nagyon pontosan leírja a világunk fizikai terét, amelyben élünk, de ez nem logikai szükségszerűség – csak éppen a fizikai világ egy (majdnem egzakt) megfigyelt tulajdonsága.Valóban van egy másik, a Bolyai–Lobacsevszkij-féle (vagy hiperbolikus) geometria,72 amely a legtöbb tekintetben nagyon hasonló az euklideszihez, de vannak bizonyos érdekes különbségek. Emlékezzünk például arra, hogy az euklideszi geometriában minden háromszög szögeinek összege 180°. A Bolyai–Lobacsevszkij-geometriában ez az összeg mindig kevesebb, mint 180°, a különbség arányos a háromszög területével (lásd az 5.1. ábrát).
Nagyon könnyen előfordulhat, hogy a Bolyai–Lobacsevszkij-geometria kozmikus skálán érvényes világunkra (lásd 7. fejezet). Azonban a háromszög szöghiánya és területe közötti arányossági tényező ebben az esetben rendkívül kicsi kellene legyen, és az euklideszi geometria bármilyen közönséges skálán kitűnő közelítése volna ennek a geometriának. Einstein általános relativitáselmélete, mint e fejezetben később látni fogjuk, valójában azt mondja nekünk, hogy világunk geometriája a kozmológiainál sokkal kisebb skálákon eltér az euklideszitől (noha olyan „szabálytalan” módon, ami sokkal bonyolultabb a Bolyai–Lobacsevszkij-geometriánál), bár közvetlen tapasztalataink közönséges skáláján az eltérések még mindig nagyon kicsik.
Távol attól, hogy logikai szükségszerűség legyen, tapasztalatilag megfigyelt tény az, hogy az euklideszi geometria olyan pontosan – ha nem is teljesen egzaktul – illik fizikai terünk szerkezetére! Az euklideszi geometria valójában mindvégig (SZUPER) fizikai elmélet volt azon felül, hogy a tiszta matematika elegáns és logikus darabja.Bizonyos értelemben nincs nagyon messze ez a Platón által kedvelt filozófiai nézőponttól (i. e. 360 körül; úgy ötven évvel Eukleidész Elemek című, a geometriáról szóló könyve előtt). Platónnál a tiszta geometria tárgyai – egyenes vonalak, körök, háromszögek, síkok stb. – csak közelítőleg valósulnak meg az igazi fizikai dolgok világában. A tiszta geometriának ezek a matematikailag pontos tárgyai egy másik világot népesítenek be, a matematikai fogalmak platóni ideális világát. Platón világa nem tapintható tárgyakat tartalmaz, hanem matematikai dolgokat. Ez a világ számunkra nem a megszokott fizikai módon érhető el, hanem az értelem útján. Eszünk mindig akkor lép érintkezésbe Platón világával, amikor a matematikai gondolkodás és meglátás gyakorlatával felfog egy matematikai igazságot. Ezt az idealizált világot különállónak tekintették és tökéletesebbnek külső tapasztalásaink anyagi világánál, de éppen olyan valódinak. (Emlékezzünk vissza fejtegetéseinkre a matematikai fogalmak platóni valóságáról a 3. és 4. fejezetekben.) Így amíg a tiszta euklideszi geometria tárgyait gondolatban lehet tanulmányozni, és ezáltal le lehet vezetni az ideális világ sok tulajdonságát, az nem szükségszerű, hogy a külső tapasztalás tökéletlen fizikai világa pontosan tapadjon ehhez az ideális világhoz. Úgy látszik, hogy valamilyen varázslatos meglátás révén és a saját idejében minden bizonnyal nagyon szórványos bizonyítékok alapján Platón előre látta, hogy: egyrészt a matematikát önmagáért kell tanulmányozni és megérteni, és nem kell megkövetelni, hogy teljesen pontosan alkalmazható legyen a fizikai tapasztalat tárgyaira; másrészt a valóságos, külső világot végül is csak a precíz matematika alapján lehet megérteni – azaz Platón az értelem útján elérhető ideális világa alapján!Most azonban az Akadémia egy másik tagjával fogunk foglalkozni – aki valamivel kevésbé ismert, mint Arisztotelész, de szerintem sokkal finomabb tudós –, az ókor egyik nagy gondolkodójával, a matematikus és csillagász Eudoxosszal.Az euklideszi geometriának van egy mély és finom tartozéka – valójában az egyik leglényegesebb –, amit manapság aligha gondolnánk geometriának! (A matematikusok inkább „analízisnek” neveznék, mint „geometriának”.) Ez a tartozék a valós számok bevezetése. Az euklideszi geometria távolságokra és szögekre vonatkozik. Hogy e geometriát megértsük, fel kell fognunk, milyen típusú számokra van szükség a távolságok és szögek leírásához. A központi új elképzelést Eudoxosz (kb. i. e. 408–355) vetette fel a 4. században időszámításunk előtt.73 A görög geometria „krízist” élt át a pitagoreusok azon felfedezése következtében, hogy az olyan számok, mint a (amelyre azért van szükség, hogy a négyzet átlóját kifejezhessük az oldal hosszával), nem írhatók fel törtként (vö. 3. fejezet). A görögök számára fontos volt, hogy a geometriai méreteket (arányokat) ki tudják fejezni egészekkel (egészek hányadosaival), mert így a geometriai nagyságokat az aritmetika törvényei szerint tudták tanulmányozni.Penrose nem nagyon kedveli a szellem világával szemben az anyagi világ elsődlegességét hirdetőket. Lám "szegény" Arisztotelész nem eléggé finom tudós szerinte...Hozzám, aki inkább a két világ határánszeret bóklászni Arisztotelész és az általa képviselt irány közelebb áll, Platon világa viszont nagyon költői, messzelebegő fátyol, csillagköd az "éterben". Úgyhogy: pro primo, pro secondo, de a kettő együtt az egész. Van azonban egy lényeges különbség Eudoxosz, illetve Dedekind és Weierstrass javaslatai között. Az ókori görögök úgy gondoltak a valós számokra, mint adott dolgokra – geometriai méretekkel (azok arányaival) kifejezve –, azaz a „valóságos” tér tulajdonságaira. Számukra szükséges volt, hogy a geometriai méreteket az aritmetikával tudják kezelni, hogy szigorúan tudjanak beszélni róluk, és összegeikről és szorzataikról is – lényeges összetevői ezek az ókoriak oly sok csodálatos geometriai tételének. (Az 5.3. ábrán illusztrációként bemutatom a nevezetes Ptolemaiosz-tételt – bár Ptolemaiosz Eudoxosz koránál jóval később fedezte azt fel – egy körön lévő négy pont közötti távolságok kapcsolatáról, amely szépen mutatja, hogy az összegekre és szorzatokra is szükség van.) Eudoxosz feltételei rendkívül gyümölcsözőknek bizonyultak, például ezek tették lehetővé a görögök számára a területek és térfogatok szabatos számítását.
Azonban a 19. század matematikusai számára – és valójában a maiak számára is – megváltozott a geometria szerepe. Az ókori görögöknek és különösen Eudoxosznak a „valós” számok olyan dolgok voltak, amelyeket a fizikai tér geometriájából kellett „kihámozniuk”. Ma jobban szeretünk úgy gondolni a valós számokra, mint amelyek a geometriánál logikailag primitívebbek. Ez teszi lehetővé számunkra, hogy felépítsük a különböző típusú geometriák minden fajtáját, mindegyiket a szám fogalmából kiindulva. (Az alapeszme a koordinátageometria, amit a 17. században vezetett be Fermat és Descartes. A koordináták felhasználhatók más típusú geometriák definiálására.) Bármelyik ilyen „geometria” logikailag konzisztens kell legyen, de nem kell, hogy közvetlenül kapcsolódjék tapasztalataink fizikai teréhez. Az a speciális fizikai geometria, amelyet látszólag érzékelünk, a tapasztalat egy idealizációja (függ például attól, hogyan extrapolálunk a végtelenül nagy vagy kicsi méretekhez, vö. 3. fejezet), de a kísérletek ma elég pontosak ahhoz, hogy fel kelljen fognunk, „tapasztalt” geometriánk valóban különbözik az euklideszi ideálistól, és összhangban van azzal, amit Einstein általános relativitáselmélete mond. Ám a fizikai világ geometriájáról alkotott nézetünk változásai ellenére Eudoxosz 23 évszázados valósszám-fogalma lényegében változatlan maradt, és Einstein elméletének éppen olyan lényeges összetevője, mint Eukleidészének. Valójában minden eddigi komoly fizikai elméletnek lényeges alkotórésze!Eukleidész Elemekjének ötödik könyve alapjában az Eudoxosz által bevezetett és az előbb leírt „arányosságelmélet” kifejtése. Ez alapvetően fontos volt a mű egésze számára. Az először i. e. 300 körül kiadott teljes Elemeket valóban úgy kell értékelnünk, mint minden idők egyik legmélyebb hatású könyvét. Ez a mű teremtette meg majdnem minden későbbi tudományos és matematikai gondolkodás színpadát. Módszerei deduktívak voltak, világosan felállított axiómákból indultak ki, amelyekről feltételezte, hogy a tér „magától értetődő” tulajdonságai; és számos következményt vezetett le, közülük sok a meglepő és fontos és egyáltalán nem magától értetődő. Nem vitás, hogy Eukleidész műve mély hatást gyakorolt a tudományos gondolkodás elkövetkező fejlődésére.
-------------------------------------------------------------------------------------------------------------------- ----------------------------------Galilei és Newton dinamikája
 Newton meg tudta mutatni, hogy Kepler három törvénye következik az ő általános rendszeréből (inverz négyzetes vonzási erőtörvény mellett). Ezen kívül megkapott minden részletes korrekciót Kepler ellipszispályáihoz, és más jelenségeket is, mint például a napéjegyenlőség precesszióját (a Föld forgástengelye irányának lassú mozgását, amelyet a görögök az évszázadok során megfigyeltek). Hogy mindezeket elérje, Newtonnak – a differenciálszámítás mellett – sok matematikai technikát kellett kidolgoznia. Erőfeszítéseinek tüneményes sikerét nagyban köszönhette kiemelkedő matematikai ügyességének és nem kevésbé nagyszerű fizikai meglátásainak.
Newton meg tudta mutatni, hogy Kepler három törvénye következik az ő általános rendszeréből (inverz négyzetes vonzási erőtörvény mellett). Ezen kívül megkapott minden részletes korrekciót Kepler ellipszispályáihoz, és más jelenségeket is, mint például a napéjegyenlőség precesszióját (a Föld forgástengelye irányának lassú mozgását, amelyet a görögök az évszázadok során megfigyeltek). Hogy mindezeket elérje, Newtonnak – a differenciálszámítás mellett – sok matematikai technikát kellett kidolgoznia. Erőfeszítéseinek tüneményes sikerét nagyban köszönhette kiemelkedő matematikai ügyességének és nem kevésbé nagyszerű fizikai meglátásainak.Kiszámítható-e az élet a biliárdgolyó-világban?
Bármelyik determinisztikus fizikai elméletről megkérdezhetjük, hogy kiszámítható-e vagy sem. Valóban, kiszámítható-e a newtoni biliárdgolyó-világ?
A fizikai kiszámíthatóság kérdése részben attól függ, milyen kérdéseket akarunk a rendszernek feltenni. Van azonban olyan értelmezés, amelyben e világ a gyakorlatban „nem kiszámítható”. Ez abból a körülményből ered, hogy mindig korlátozott az a pontosság, amellyel a kezdeti adatokat ismerni lehet. Ténylegesen nagyon jelentős „instabilitás” van inherensen jelen az ilyen típusú problémában. Nagyon pici változás a kezdeti adatokban gyorsan roppant nagy változást idézhet elő az eredő viselkedésben. Az ilyen típusú instabilitásra gyakran használják a „káosz” vagy „kaotikus viselkedés” kifejezéseket. Fontos a kaotikus viselkedés például az időjárásban. Noha az elemeket kormányzó Newton-egyenletek jól ismertek, a hosszú távú időjárási előrejelzések közismerten megbízhatatlanok!Ez egyáltalán nem az a fajta „nemkiszámíthatóság”, amelyet bármilyen módon „ki lehet aknázni”. Csupán annyiról van szó, hogy mert a kezdeti állapot csak korlátozott pontossággal ismerhető, a jövőbeli állapot a kezdetiből nem kiszámítható megbízhatóan. Valójában egy „véletlenszerű elem” kerül be a jövőbeli viselkedésbe, de ennyi az egész. Ha az agy valóban hasznos nem kiszámítható elemeket aknáz ki a fizikai törvényekben, akkor ezeknek a fentitől egészen különbözőeknek és sokkal pozitívabbaknak kell lenniük. Ennek megfelelően erre a fajta „kaotikus” viselkedésre egyáltalán nem fogom használni a „nem kiszámítható” kifejezést, inkább a „jósolhatatlant”. A jósolhatatlanság jelenléte nagyon általános jelenség az olyan jellegű determinisztikus törvényekben, amelyek a (klasszikus) fizikában ténylegesen fellépnek, ezt hamarosan látni fogjuk. A jósolhatatlanság biztosan olyan dolog, amelyet egy gondolkodó gép készítése során minimalizálni szeretnénk, nem pedig „kiaknázni”!
Hamiltoni mechanika
A newtoni mechanika sikereit nemcsak az eredményezte, hogy nagyszerűen alkalmazható a fizikai világra, hanem a belőle kinövő matematikai elmélet gazdagsága is. Figyelemre méltó, hogy a Természet minden SZUPER elmélete a matematikai ideák rendkívül termékeny forrásának bizonyult. Mély és szép titok van abban a tényben, hogy e szuperpontos elméletek mint egyszerű matematika is rendkívül gyümölcsözőek. Ez kétségtelenül mond valami mélyet nekünk a fizikai tapasztalataink valóságos világa és a matematika platóni világa közötti kapcsolatokról. (E kérdést később fogom tárgyalni a 10. fejezetben.) A newtoni mechanika talán a legfontosabb ebben a vonatkozásban, mert születése hozta meg az analízist. Mi több, a speciális newtoni rendszer a matematikai gondolatok nevezetes gyűjteményét teremtette meg, azt, amelyet klasszikus mechanika néven ismerünk. Fejlődéséhez hozzájárult a tizennyolcadik és tizenkilencedik század sok nagy matematikusa: Euler, Lagrange, Laplace, Liouville, Poisson, Jacobi, Osztrogradszkij, Hamilton. E munka nagy részét foglalja magában az, amit „Hamilton-elméletnek”81 nevezünk. A hamiltoni rendszer egyik újszerű vonása a fizikai rendszer leírására használt „változókban” van. Mindeddig a részecskék helyzetét tekintettük elsődlegesnek, a sebesség egyszerűen a helyzetváltoztatás időbeli nagysága volt. Emlékezzünk rá, hogy egy newtoni rendszer kezdeti állapotának megadásához szükségünk volt minden részecske helyzetére és sebességére, hogy az ezután következő viselkedés meghatározott legyen. A hamiltoni megfogalmazásban a részecskéknek nem sebességeit, hanem impulzusait kell kiválasztanunk. (Korábban megjegyeztük, hogy egy részecske impulzusa a sebességének és a tömegének szorzata.) Ez önmagában kis változásnak tűnhet, a fontos azonban az, hogy úgy kezeljük minden részecske helyét és impulzusát, mint többé-kevésbé egyenrangú, független mennyiségeket.A Hamilton-formalizmus a mechanika nagyon elegáns, szimmetrikus leírását nyújtja. Hogy éppen csak lássuk, hogyan néznek ki, írjuk le itt az egyenleteket, még ha sok Olvasó nincs is hozzászokva az analízis jelöléseihez, amely szükséges a teljes megértéshez – most azonban nem lényeges a teljes megértés. Amit a differenciálszámításról igazán fel kell fogni, az annyi, hogy az egyenletek bal oldalán megjelenő „pont” az időbeli változás sebességét jelöli (az impulzusét az első egyenletben, a helyét a másodikban): Itt az i indexet a különböző p1, p2, p3, p4, … impulzus- és x1, x2, x3, x4, … helykoordináták megkülönböztetésére használjuk. n szabad részecske esetén 3n impulzuskoordinátánk és 3n helykoordinátánk lesz (a három független térbeli irány mindegyikéhez egy). A ∂ szimbólum a „parciális differenciálás” jele („az olyan differenciálásé, amikor minden más változót állandónak tartunk”), H pedig az előbb leírt Hamilton-függvény. Az x1, x2, … és pl, p2, … koordináták valójában sokkal általánosabb dolgok lehetnek, mint a részecskék közönséges Descartes-koordinátái (azaz az xi-k a közönséges távolságok három egymásra merőleges irányban mérve). Egyes xi koordináták lehetnek például szögek (amikor is a megfelelő pi-k impulzusmomentumok, és nem impulzusok), vagy valamilyen más, egészen általános mértékek. Figyelemre méltó, hogy a Hamilton-egyenletek pontosan ugyanolyan alakúak maradnak. Valójában H alkalmas megválasztásával a Hamilton-egyenletek érvényesek maradnak bármilyen klasszikus egyenletrendszerre, nem csak a Newton-egyenletekre. Fennáll ez a Maxwell(–Lorentz)-elméletre is, amelyet rövidesen megvizsgálunk. A Hamilton-egyenletek érvényesek a speciális relativitáselméletben is. Megfelelő gondossággal még az általános relativitáselmélet is beilleszthető a hamiltoni keretbe. Továbbá, ahogy azt később a Schrödinger-egyenletnél látni fogjuk (6. fejezet), ez a hamiltoni keret szolgáltatja az összehasonlító pontot a kvantummechanika egyenletei számára. Igazán figyelemreméltó, hogy bár a fizikai elméletek a múlt században és azután forradalmi változásokon mentek keresztül, a dinamikai egyenletek szerkezetében ilyen formai egység mutatkozik!
Fázistér
A Hamilton-egyenletek alakja lehetővé teszi, hogy nagyon hatásos és általános módon jelenítsük meg egy klasszikus rendszer fejlődését. Próbáljunk elképzelni egy nagy dimenziószámú „teret”, minden x1, x2, …, p1, p2, … koordinátához tartozzék egy dimenzió. (Matematikai tereknek gyakran van háromnál több dimenziójuk.) Ennek a térnek a neve fázistér (lásd 5.10. ábra), n szabad részecske esetén 6n a dimenziószáma (minden részecskéhez három hely- és három impulzuskoordináta tartozik). Az Olvasó joggal aggódhat, hogy ez már egyetlen részecskénél is kétszer annyi dimenzió, mint amennyit a megjelenítésre rendesen használni szokott! A dolog titka az, hogy nem szabad megijedni. Noha hat dimenzió valóban több, mint amennyit könnyen(!) lehet ábrázolni, valójában nem is volna sok haszna annak, ha képesek volnánk ábrázolni. Egy levegőmolekulákkal teli szoba olyan rendszer, amelynél a fázistér dimenzióinak száma 10 000 000 000 000 000 000 000 000 000
körüli lehet. Ilyen nagy tér pontos megjelenítését megpróbálni nem sok reménnyel kecsegtet! A trükk az, hogy meg se próbáljuk – még egyetlen részecske fázisterét sem. Csak gondoljunk el valami homályos háromdimenziós (sőt kétdimenziós) tartományra. Vessünk egy pillantást az 5.10. ábrára. Ez teljesen kielégítő lesz.
A fázistérbeli szétszóródásnak van egy másik nevezetes vonzata. Valójában azt mondja, hogy a klasszikus mechanika nem lehet érvényes világunkra! E következményt valamennyire eltúloztam, de talán nem olyan nagyon. A klasszikus mechanika jól számot tud adni a folyékony testek viselkedéséről – különösen a gázokéról, de a folyadékokéról is elég jól –, ahol a részecskerendszereknek csak „átlagolt” tulajdonságaival törődünk, de nehézségei vannak a szilárd testek szerkezetével kapcsolatban, ahol részletesebb rendezett szerkezetre van szükség. Probléma az, hogyan tarthatja meg alakját egy szilárd test, mikor pontszerű részecskék miriádjaiból áll össze, amelyek szervezett elrendezése a fázistérbeli szétszóródás miatt folyamatosan gyengül. Ma már tudjuk, a kvantumelméletre van szükség ahhoz, hogy a szilárd testek tényleges szerkezetét megfelelően megérthessük. A kvantumos jelenségek valahogyan meg tudják akadályozni ezt a fázistérbeli szétszóródást. A kérdés fontos, később majd vissza kell rá térnünk (lásd a 8. és 9. fejezetet).
A probléma a „számítógép-készítés” kérdésében is lényeges. A fázistérbeli szétfolyás olyan dolog, amit ellenőrzés alatt kell tartani. Nem engedhető meg, hogy egy számítóeszköz „diszkrét” állapotának megfelelő fázistértartomány (mint az előbbiekben leírt R0) túlságosan szétfolyjék. Emlékezzünk vissza, hogy még a Fredkin–Toffoli-féle „biliárdgolyó-számítógépnek” is különálló, szilárd falakra van szüksége, hogy működni tudjon. Egy sok részecskéből összetevődő tárgy „szilárdságának” a működési feltétele a kvantummechanika. Úgy látszik, hogy még egy „klasszikus” számítómasinának is kölcsönöznie kell a kvantumfizika jelenségeiből, hogy hatékonyan működjék!
A probléma a „számítógép-készítés” kérdésében is lényeges. A fázistérbeli szétfolyás olyan dolog, amit ellenőrzés alatt kell tartani. Nem engedhető meg, hogy egy számítóeszköz „diszkrét” állapotának megfelelő fázistértartomány (mint az előbbiekben leírt R0) túlságosan szétfolyjék. Emlékezzünk vissza, hogy még a Fredkin–Toffoli-féle „biliárdgolyó-számítógépnek” is különálló, szilárd falakra van szüksége, hogy működni tudjon. Egy sok részecskéből összetevődő tárgy „szilárdságának” a működési feltétele a kvantummechanika. Úgy látszik, hogy még egy „klasszikus” számítómasinának is kölcsönöznie kell a kvantumfizika jelenségeiből, hogy hatékonyan működjék!
Maxwell elektromágneses elmélete
A világ newtoni képében piciny részecskékre gondolunk, ezek egymásra a közöttük lévő távolságtól függő erővel hatnak – ha pedig nem teljesen pontszerűek, akkor alkalmanként, a tényleges fizikai érintkezéskor visszapattannak egymásról. Mint már előbb említettem, az elektromos és mágneses erők (mindkettő létezéséről az ókor óta tudnak, részletesebben William Gilbert 1600-ban és Benjamin Franklin 1752-ben kezdte tanulmányozni azokat) a gravitációs erőkhöz hasonlóan hatnak, amennyiben szintén a távolság négyzetével fordított arányban csökkennek, viszont inkább taszítóak, mint vonzóak – azaz hasonló a hasonlót taszítja –, és nem a tömeg, hanem az elektromos töltés (illetve a mágneses pólus erőssége) szabja meg az erő nagyságát. Ezen a szinten az elektromosság és a mágnesség nehézség nélkül beilleszthető a newtoni sémába. A fény viselkedése nagyjából (bár némi határozott nehézséggel) szintén leírható vagy úgy, hogy egyedi részecskékből (fotonokból, ahogy ma mondjuk) összeállónak tekintjük, vagy hullámmozgásnak valamilyen közegben, ez utóbbi esetben magát a közeget („étert”) is részecskékből állónak kell gondolnunk.
A világ newtoni képében piciny részecskékre gondolunk, ezek egymásra a közöttük lévő távolságtól függő erővel hatnak – ha pedig nem teljesen pontszerűek, akkor alkalmanként, a tényleges fizikai érintkezéskor visszapattannak egymásról. Mint már előbb említettem, az elektromos és mágneses erők (mindkettő létezéséről az ókor óta tudnak, részletesebben William Gilbert 1600-ban és Benjamin Franklin 1752-ben kezdte tanulmányozni azokat) a gravitációs erőkhöz hasonlóan hatnak, amennyiben szintén a távolság négyzetével fordított arányban csökkennek, viszont inkább taszítóak, mint vonzóak – azaz hasonló a hasonlót taszítja –, és nem a tömeg, hanem az elektromos töltés (illetve a mágneses pólus erőssége) szabja meg az erő nagyságát. Ezen a szinten az elektromosság és a mágnesség nehézség nélkül beilleszthető a newtoni sémába. A fény viselkedése nagyjából (bár némi határozott nehézséggel) szintén leírható vagy úgy, hogy egyedi részecskékből (fotonokból, ahogy ma mondjuk) összeállónak tekintjük, vagy hullámmozgásnak valamilyen közegben, ez utóbbi esetben magát a közeget („étert”) is részecskékből állónak kell gondolnunk.
Tekintsünk először egy mágneses mezőt! A legtöbb Olvasó már látta, hogyan viselkedik a vasreszelék, ha olyan papírra szórjuk, amely alatt mágnes van. A vasreszelék meglepő módon felsorakozik az ún. „mágneses erővonalak” mentén. Úgy képzeljük, hogy az erővonalak akkor is ott maradnak, amikor a vasreszelék nincs ott. Ezek képezik azt, amit mágneses mezőnek nevezünk. Ez a „mező” a tér minden pontjában egy bizonyos irányba mutat, nevezetesen az erővonalak irányába. Ténylegesen egy vektorunk van minden pontban, így a mágneses mező a vektormezőknek egy példája. (Összehasonlíthatnánk a hamiltoni vektormezővel, amelyről az előző szakaszban volt szó, de ez a vektormező most a közönséges térben van, nem a fázistérben.) Hasonlóképpen, egy elektromosan töltött testet egy másfajta mező, az elektromos mező vesz körül, és minden tömeges testet hasonlóan egy gravitációs mező. Ezek is vektormezők a térben.
Ilyen elképzelések már régen Faraday előtt ismertek voltak, és az elméletiek fegyvertárának nagyon komoly részévé váltak a newtoni mechanikában. Azonban az uralkodó nézőpont az ilyen „mezőket” nem tekintette valódi fizikai szubsztanciának. Inkább úgy gondolták, hogy ezekkel lehet „számon tartani” az erőket, amelyek hatnának, ha egy megfelelő részecskét helyeznének a különböző pontokba. Faradayt azonban alapvető kísérleti felfedezései (mozgó tekercsekkel, mágnesekkel és hasonlókkal) arra vezették, hogy az elektromos és mágneses mezőket „valóságos” fizikai anyagnak higgye, sőt mi több, úgy gondolta, hogy a változó elektromos és mágneses mezők olykor képesek egymást az egyébként üres téren „keresztültolni”, így hoznak létre egyfajta testetlen hullámot! Feltételezte, hogy a fény maga is ilyen hullámokból állhat. Ez a nézet eltért az uralkodó „newtoni bölcsességtől”, amelyben az ilyen mezőket semmilyen értelemben nem gondolták „valóságosaknak”, csak kényelmes matematikai segédeszközöknek a „valóság” „igazi” newtoni pontrészecske-távolhatás képéhez.
Ilyen elképzelések már régen Faraday előtt ismertek voltak, és az elméletiek fegyvertárának nagyon komoly részévé váltak a newtoni mechanikában. Azonban az uralkodó nézőpont az ilyen „mezőket” nem tekintette valódi fizikai szubsztanciának. Inkább úgy gondolták, hogy ezekkel lehet „számon tartani” az erőket, amelyek hatnának, ha egy megfelelő részecskét helyeznének a különböző pontokba. Faradayt azonban alapvető kísérleti felfedezései (mozgó tekercsekkel, mágnesekkel és hasonlókkal) arra vezették, hogy az elektromos és mágneses mezőket „valóságos” fizikai anyagnak higgye, sőt mi több, úgy gondolta, hogy a változó elektromos és mágneses mezők olykor képesek egymást az egyébként üres téren „keresztültolni”, így hoznak létre egyfajta testetlen hullámot! Feltételezte, hogy a fény maga is ilyen hullámokból állhat. Ez a nézet eltért az uralkodó „newtoni bölcsességtől”, amelyben az ilyen mezőket semmilyen értelemben nem gondolták „valóságosaknak”, csak kényelmes matematikai segédeszközöknek a „valóság” „igazi” newtoni pontrészecske-távolhatás képéhez.
Szembetalálva magát Faraday kísérleti felfedezéseivel, meg a neves francia fizikus, André Marie Ampère (1775–1836) és mások korábbi eredményeivel és megihletve Faraday látomása által James Clerk Maxwell (1831–1879), a nagy skót fizikus és matematikus, eltűnődött az elektromos és mágneses mezőkre vonatkozó egyenletek matematikai alakján. Figyelemre méltó meglátással változtatást javasolt az egyenletekben – látszólag talán eléggé csekélyet, de következményeit tekintve alapvetőt. E változtatást egyáltalán nem az ismert kísérleti tények sugallták (bár azokkal összhangban volt), Maxwell saját elméleti, részben fizikai, részben matematikai és részben esztétikai követelményeinek eredménye volt. A Maxwell-egyenletek egyik következménye, hogy az elektromos és mágneses mezők valóban „tolják” egymást az üres téren keresztül. Egy oszcilláló mágneses mező oszcilláló elektromos mezőt kelt (ezt Faraday kísérleti felfedezése sugallta), ez az oszcilláló elektromos mező viszont oszcilláló mágneses mezőt (ami Maxwell elméleti következtetése), ez újra elektromos mezőt és így tovább. (Az ilyen hullámok részletes képét illetően lásd a 6.26., 6.27. ábrákat.) Maxwell ki tudta számítani, milyen sebességgel terjed e hatás a térben – és azt találta, hogy ez a fény sebessége! Ezek az ún. elektromágneses hullámok mutatják továbbá az interferenciát és a fény rejtélyes polarizációs tulajdonságait, amelyeket már régóta ismertek (ezekkel a 6. fejezetben fogunk találkozni). Amellett, hogy számot adott a látható fény tulajdonságairól, amikor a hullámhossz egy meghatározott tartományba esik (4 – 7 ∙ 10–7 m), más hullámhosszú elektromágneses hullámokat is megjósolt, amelyeket huzalban folyó elektromos áram kelt. E hullámok létezését kísérletileg a híres német fizikus, Heinrich Hertz mutatta ki 1888-ban. Faraday ihletett reménysége valóban szilárd alapra lelt a csodálatos Maxwell-egyenletekben! ... 
Itt E, B és j rendre az elektromos mezőt, a mágneses mezőt és az elektromos áramot leíró vektormezők; ρ az elektromos töltéssűrűség, c pedig egy állandó, a fény sebessége.84 A „rot” és „div” jelölésekkel ne törődjünk, ezek különböző térbeli változásokra utalnak. (A térkoordináta szerinti parciális differenciálások bizonyos kombinációi. Emlékezzünk vissza a parciális differenciálás ∂ szimbólummal jelölt műveletére, amellyel a Hamilton-egyenleteknél már találkoztunk.) Az első két egyenlet bal oldalán látható ∂/∂t operátor tulajdonképpen ugyanaz, mint a Hamilton-egyenletekben használt „pont”, a különbség csupán technikai. Így ∂E/∂t „az elektromos mező változási sebességét”, ∂B/∂t „a mágneses mező változási sebességét” jelöli. Az első egyenlet85 megmondja, hogyan változik időben az elektromos mező attól függően, mit csinál pillanatnyilag a mágneses mező és az elektromos áram; a második egyenlet azt mondja meg, hogyan változik időben a mágneses mező attól függően, mit csinál pillanatnyilag az elektromos mező. A harmadik egyenlet durván szólva az inverz négyzetes törvény egy rejtett alakja, megmondja, milyen kapcsolatban kell legyen az elektromos mező a pillanatnyi töltéseloszlással; míg a negyedik egyenlet ugyanez lenne a mágneses mezőre, csakhogy „mágneses töltések” (különálló északi vagy déli pólusú részecskék) nincsenek. Ezek az egyenletek annyiban hasonlítanak a Hamilton-egyenletekre, hogy megmondják, mi kell legyen a lényeges mennyiségek (most az elektromos és mágneses mező) időbeli változási sebessége az adott időpontbeli értékeikkel kifejezve. Így a Maxwell-egyenletek éppen úgy determinisztikusak, mint ahogy a közönséges Hamilton-egyenletek. Az egyetlen különbség az – és ez lényeges különbség –, hogy a Maxwell-egyenletek nem részecske-, hanem mezőegyenletek, ami annyit jelent, hogy a rendszer állapotának leírásához végtelen számú paraméterre van szükség (a mező vektorokra a tér minden egyes pontjában), és nem véges számúra, mint a részecskeelméletben (három hely- és három impulzuskoordinátára minden részecskénél). Így a Maxwell-elméletnél a fázistér egy végtelen dimenziószámú tér! (Mint korábban említettem, a Maxwell-egyenleteket ténylegesen be lehet illeszteni az általános hamiltoni keretbe, de ezt a keretet a végtelen dimenzió miatt egy kissé ki kell tágítani.)86 A fizikai valóságról alkotott képünkben, ahogy azt a Maxwell-elmélet mutatja, az előző eseten túlmenően az az alapvetően új alkotórész, hogy most mezőket kell saját jogukon komolyan vennünk, nem lehet ezeket csupán a newtoni elmélet „valódi” részecskéihez tartozó matematikai függeléknek tekintenünk. Maxwell megmutatta, hogy amikor a mezők elektromágneses hullámként terjednek, határozott mennyiségű energiát visznek magukkal. Meg tudta adni ennek az energiának explicit kifejezését. E figyelemre méltó tényt, hogy ezekkel a „testetlen” elektromágneses hullámokkal energiát lehet helyről helyre szállítani, kísérletileg az erősítette meg, hogy Hertz észlelt ilyen hullámokat. Olvasónapló, olyan ez. Magamnak jegyzem, idézem Penrose írását hosszan. Simonyi Károly A Fizika kultúrtörténete c. könyve hasonló olvasmány. 'Olyan unalmas ez a munka, egész nap az irodában ülve, 'mint egy most- fizikapéldákat- fogunk- megoldani óra Gizusnál '- írja Orsi nekem 69 nyarán. Szegény Gizus, szegény Orsi.
Szembetalálva magát Faraday kísérleti felfedezéseivel, meg a neves francia fizikus, André Marie Ampère (1775–1836) és mások korábbi eredményeivel és megihletve Faraday látomása által James Clerk Maxwell (1831–1879), a nagy skót fizikus és matematikus, eltűnődött az elektromos és mágneses mezőkre vonatkozó egyenletek matematikai alakján. Figyelemre méltó meglátással változtatást javasolt az egyenletekben – látszólag talán eléggé csekélyet, de következményeit tekintve alapvetőt. E változtatást egyáltalán nem az ismert kísérleti tények sugallták (bár azokkal összhangban volt), Maxwell saját elméleti, részben fizikai, részben matematikai és részben esztétikai követelményeinek eredménye volt. A Maxwell-egyenletek egyik következménye, hogy az elektromos és mágneses mezők valóban „tolják” egymást az üres téren keresztül. Egy oszcilláló mágneses mező oszcilláló elektromos mezőt kelt (ezt Faraday kísérleti felfedezése sugallta), ez az oszcilláló elektromos mező viszont oszcilláló mágneses mezőt (ami Maxwell elméleti következtetése), ez újra elektromos mezőt és így tovább. (Az ilyen hullámok részletes képét illetően lásd a 6.26., 6.27. ábrákat.) Maxwell ki tudta számítani, milyen sebességgel terjed e hatás a térben – és azt találta, hogy ez a fény sebessége! Ezek az ún. elektromágneses hullámok mutatják továbbá az interferenciát és a fény rejtélyes polarizációs tulajdonságait, amelyeket már régóta ismertek (ezekkel a 6. fejezetben fogunk találkozni). Amellett, hogy számot adott a látható fény tulajdonságairól, amikor a hullámhossz egy meghatározott tartományba esik (4 – 7 ∙ 10–7 m), más hullámhosszú elektromágneses hullámokat is megjósolt, amelyeket huzalban folyó elektromos áram kelt. E hullámok létezését kísérletileg a híres német fizikus, Heinrich Hertz mutatta ki 1888-ban. Faraday ihletett reménysége valóban szilárd alapra lelt a csodálatos Maxwell-egyenletekben! ...
Kiszámíthatóság és a hullámegyenlet
Maxwell egyenleteiből képes volt közvetlenül levezetni, hogy a tér azon tartományaiban, ahol töltések és áramok nincsenek (azaz, ahol j = 0, ρ = 0 a fenti egyenletekben), ott az elektromos és a mágneses mező minden komponensének ki kell elégítenie egy hullámegyenlet néven ismert egyenletet.87 A hullámegyenlet a Maxwell-egyenletek „egyszerűsített változatának” tekinthető, mert egyetlen mennyiségre vonatkozó egyenlet, nem szerepel benne az elektromos és mágneses mezőknek mind a hat komponense. Megoldásai hullámszerű viselkedést mutatnak, s nem rendelkeznek olyanféle járulékos bonyodalmakkal, mint a Maxwell-elmélet „polarizációja” (az elektromos vektormező iránya, lásd 6. fejezet).Marian Boykan Pour-El és Ian Richards (1979, 1981, 1982) meg tudták mutatni, hogy bár a hullámegyenletek megoldásai a szokásos értelemben determinisztikusan viselkednek – azaz egy kezdeti időpontban előírt adatok meghatározzák a megoldást minden más időpontban –, léteznek bizonyos „sajátos” jellegű kiszámítható kezdeti adatok, amelyeknek megvan az a tulajdonságuk, hogy a mező elvileg meghatározott értéke egy későbbi kiszámítható időpontban ténylegesen nem kiszámítható. Így egy tetszetős fizikai mezőelmélet (jóllehet nem a mi világunkra ténylegesen igaz Maxwell-elmélet) egyenletei a Pour-El- és Richards-féle értelemben mutathatnak nem kiszámítható fejlődést!Míg azonban a Pour-El–Richards-féle eredmény bizonyára meglepő és matematikailag lényeges, fizikai értelemben valójában nem mond ellent a sejtésnek. A kiszámíthatósági sejtésnek.Pour-El és Richards ténylegesen bebizonyították, hogy a hullámegyenletben nem léphet fel nemkiszámíthatóság, ha az ilyen jellegű mezőt nem engedjük meg. Mindenesetre még ha meg is engedjük, nehezen látható, hogyan használhatná ki az ilyen nemkiszámíthatóságot bármilyen fizikai „eszköz” (mint az emberi agy?). Jelentősége csak akkor lehet, ha tetszőlegesen pontos méréseket engedünk meg, ami, mint korábban leírtam, fizikailag nem nagyon valószerű. Mindazonáltal a Pour-El–Richards-féle eredmények egy olyan fontos kutatás érdekes kezdeteit jelentik, amelyben eddig még keveset végeztek.
A Lorentz-féle mozgásegyenlet; elfutó részecskék
A Maxwell-egyenletek önmagukban nem alkotnak igazán teljes egyenletrendszert. Csodálatosan leírják az elektromos és mágneses mező terjedését, ha adott az elektromos töltések és áramok eloszlása. E töltések fizikailag töltött részecskék – ahogy ma tudjuk, főként elektronok és protonok –, az áramok pedig e részecskék mozgásából származnak. Ha tudjuk, hol vannak a részecskék és hogyan mozognak, akkor a Maxwell-egyenletek megmondják, hogyan viselkedik az elektromágneses mező. Nem mondják meg viszont, hogyan viselkednek maguk a részecskék. A kérdésre a választ részben már Maxwell idejében ismerték, de kielégítő egyenletrendszert 1895-ig nem írtak fel. Ekkor Hendrick Antoon Lorentz a speciális relativitáselmélettel rokon elképzeléseket használva levezette azt, amit ma egy töltött részecske Lorentz-féle mozgásegyenletének nevezünk (vö. Whittaker 1910, 310., 395. o.). Ezek az egyenletek megmondják, hogyan változik folytonosan egy töltött részecske sebessége az elektromos és mágneses mezőnek azon pontbeli értékétől függően, ahol a részecske éppen található.89 Ha a Maxwell-egyenletekhez hozzátesszük a Lorentz-egyenleteket, akkor megkapjuk mind a töltött részecskék, mind az elektromágneses mező időbeli fejlődésének szabályait.Nincs azonban minden rendben ezzel az egyenletrendszerrel. Kitűnő eredményeket ad akkor, ha a mezők nagyon egyenletesek egészen a részecskék átmérőinek méretéig lemenő skálákig (e méretnek az elektron „klasszikus sugarát” vesszük, ami kb. 10–15 m), és ha a részecskék mozgása nem túl heves. Van azonban itt egy elvi nehézség, amely más körülmények között fontos lehet. A Lorentz-egyenlet azt mondja nekünk, vizsgáljuk meg az elektromágneses mezőt pontosan abban a pontban, amelyben a töltött részecske van (hogy megtudjuk az „erőt” abban a pontban). Hol legyen ez a pont, ha a részecske mérete véges? Vegyük talán a részecske „középpontját”, vagy átlagoljuk a mezőt (hogy az erőt megkapjuk) a felület pontjaira? Ez különbséget eredményezhet, ha a mező a részecske skáláján nem egyenletes. Van egy másik, komolyabb probléma: milyen is valójában a mező a részecske felületén (vagy középpontjában)? Ne felejtsük el, hogy töltött részecskéről van szó. Maga is kelt elektromágneses mezőt, ezt hozzá kell adni a „háttérmezőhöz”, amelyben a részecske ül. „Felületéhez” nagyon közel a részecske saját mezője roppant erőssé válik, könnyen elnyom minden más mezőt. Továbbá a részecske mezője körös-körül többé-kevésbé közvetlenül kifelé (befelé) mutat, így a tényleges eredő mező, amelyre a részecskének válaszolnia kell, egyáltalán nem egyenletes, a részecske „felületén” különböző helyeken különböző irányokba mutat, nem is beszélve a „belsejéről” (5.15. ábra).
 Talán jobb, ha a részecskéket pontszerűeknek tekintjük. Ez azonban másféle problémákhoz vezet, mert saját elektromos mezője a részecske közvetlen szomszédságában végtelenné válik. Ha a részecskét a Lorentz-egyenletek szerint a saját helyén lévő elektromos mező irányítja, akkor egy végtelen mezőre kell válaszolnia! Hogy a Lorentz-erőtörvénynek értelme legyen, meg kell találnunk a módját annak, hogy levonjuk a részecske saját mezőjét, és így a véges háttérmező maradjon meg, amelyre a részecske egyértelműen tud válaszolni. A problémát, hogy ezt hogyan kell csinálni, 1938-ban Dirac oldotta meg (akiről később megint fogunk hallani). Dirac megoldása azonban riasztó következtetésekhez vezetett. Azt találta, hogy a részecskék és mezők viselkedését kezdeti adataik csak akkor határozzák meg, ha nem csak kezdeti helye és sebessége ismert minden részecskének, hanem a kezdeti gyorsulások is (ami a szokásos dinamikai elméleteket tekintve eléggé rendhagyó). E kezdeti gyorsulás legtöbb értéke mellett a részecske végül teljesen őrült módon viselkedik, önmagát gyorsítja olyan sebességre, amely nagyon gyorsan közelit a fény sebességéhez! Ezek Dirac „elfutó megoldásai”, amelyek nem felelnek meg semmi olyannak, ami a Természetben valóban megtörténik. A kezdeti gyorsulások helyes megválasztásával módot kell találni az elfutó megoldások kizárására. Ez mindig megtehető, de csak úgy, ha „jövőbelátást” építünk be – azaz a kezdeti gyorsulásokat olyan módon kell előírnunk, amely előre látja, mely megoldások válnak végül elfutókká, és elkerüli ezeket. Ez egyáltalán nem az a mód, ahogy egy szabványos, determinisztikus fizikai problémában a kezdeti adatokat előírjuk. A hagyományos determinizmusban ezek az adatok tetszőlegesen adhatók meg, minden megkötés nélkül a jövőbeli viselkedést illetően. Itt most nemcsak arról van szó, hogy a jövő tökéletesen meghatározott egy múltbeli időpontban előírható adatokkal, de magát az adatok előírását nagyon pontosan megszorítja az a követelmény, hogy a jövőbeli viselkedés valóban „ésszerű” legyen!Eddig jutunk el az alapvető klasszikus egyenletekkel. Az Olvasó látja, hogy a determinizmus és a kiszámíthatóság kérdése a klasszikus fizikai törvényekben zavarossá vált. Van-e valóban teleologikus elem a fizikai törvényekben, befolyásolja-e valahogy a jövő azt, hogy mi történhetett meg a múltban? A fizikusok a klasszikus elektrodinamika (a klasszikus töltött részecskék és az elektromos és mágneses mezők elmélete) ilyen velejáróit rendesen nem tekintik a valóság komoly leírásainak. Szokásos válaszuk a fenti nehézségekre az, hogy az egyedi töltött részecskék szigorúan véve tulajdonképpen a kvantumelektrodinamika birodalmába tartoznak, és nem várhatjuk, hogy szigorúan klasszikus eljárással értelmes válaszokat kapjunk. Ez kétségtelenül igaz, de amint később látni fogjuk, magának a kvantumelméletnek is vannak e téren problémái. Dirac valójában pontosan azért vizsgálta a töltött részecskék dinamikájának klasszikus problémáját, mert úgy gondolta, hogy az ötleteket adhat a (fizikailag megfelelőbb) kvantumos probléma még nagyobb, alapvető nehézségeinek megoldásához.
Talán jobb, ha a részecskéket pontszerűeknek tekintjük. Ez azonban másféle problémákhoz vezet, mert saját elektromos mezője a részecske közvetlen szomszédságában végtelenné válik. Ha a részecskét a Lorentz-egyenletek szerint a saját helyén lévő elektromos mező irányítja, akkor egy végtelen mezőre kell válaszolnia! Hogy a Lorentz-erőtörvénynek értelme legyen, meg kell találnunk a módját annak, hogy levonjuk a részecske saját mezőjét, és így a véges háttérmező maradjon meg, amelyre a részecske egyértelműen tud válaszolni. A problémát, hogy ezt hogyan kell csinálni, 1938-ban Dirac oldotta meg (akiről később megint fogunk hallani). Dirac megoldása azonban riasztó következtetésekhez vezetett. Azt találta, hogy a részecskék és mezők viselkedését kezdeti adataik csak akkor határozzák meg, ha nem csak kezdeti helye és sebessége ismert minden részecskének, hanem a kezdeti gyorsulások is (ami a szokásos dinamikai elméleteket tekintve eléggé rendhagyó). E kezdeti gyorsulás legtöbb értéke mellett a részecske végül teljesen őrült módon viselkedik, önmagát gyorsítja olyan sebességre, amely nagyon gyorsan közelit a fény sebességéhez! Ezek Dirac „elfutó megoldásai”, amelyek nem felelnek meg semmi olyannak, ami a Természetben valóban megtörténik. A kezdeti gyorsulások helyes megválasztásával módot kell találni az elfutó megoldások kizárására. Ez mindig megtehető, de csak úgy, ha „jövőbelátást” építünk be – azaz a kezdeti gyorsulásokat olyan módon kell előírnunk, amely előre látja, mely megoldások válnak végül elfutókká, és elkerüli ezeket. Ez egyáltalán nem az a mód, ahogy egy szabványos, determinisztikus fizikai problémában a kezdeti adatokat előírjuk. A hagyományos determinizmusban ezek az adatok tetszőlegesen adhatók meg, minden megkötés nélkül a jövőbeli viselkedést illetően. Itt most nemcsak arról van szó, hogy a jövő tökéletesen meghatározott egy múltbeli időpontban előírható adatokkal, de magát az adatok előírását nagyon pontosan megszorítja az a követelmény, hogy a jövőbeli viselkedés valóban „ésszerű” legyen!Eddig jutunk el az alapvető klasszikus egyenletekkel. Az Olvasó látja, hogy a determinizmus és a kiszámíthatóság kérdése a klasszikus fizikai törvényekben zavarossá vált. Van-e valóban teleologikus elem a fizikai törvényekben, befolyásolja-e valahogy a jövő azt, hogy mi történhetett meg a múltban? A fizikusok a klasszikus elektrodinamika (a klasszikus töltött részecskék és az elektromos és mágneses mezők elmélete) ilyen velejáróit rendesen nem tekintik a valóság komoly leírásainak. Szokásos válaszuk a fenti nehézségekre az, hogy az egyedi töltött részecskék szigorúan véve tulajdonképpen a kvantumelektrodinamika birodalmába tartoznak, és nem várhatjuk, hogy szigorúan klasszikus eljárással értelmes válaszokat kapjunk. Ez kétségtelenül igaz, de amint később látni fogjuk, magának a kvantumelméletnek is vannak e téren problémái. Dirac valójában pontosan azért vizsgálta a töltött részecskék dinamikájának klasszikus problémáját, mert úgy gondolta, hogy az ötleteket adhat a (fizikailag megfelelőbb) kvantumos probléma még nagyobb, alapvető nehézségeinek megoldásához.
Einstein és Poincaré speciális relativitáselmélete
Emlékezzünk vissza a Galilei-féle relativitási elvre, amely azt mondja, hogy Galilei és Newton fizikai törvényei teljesen változatlanok maradnak, ha álló vonatkoztatási rendszerből mozgóra térünk át. Ez azzal jár, hogy a szomszédságunkban lévő objektumok dinamikai viselkedésének egyszerű vizsgálatával nem tudjuk megállapítani, vajon állunk-e vagy egyenletes sebességgel mozgunk valamilyen irányban. (Emlékezzünk Galilei hajójára a tengeren.) Tegyük azonban fel, hogy e törvényekhez hozzátesszük Maxwell egyenleteit. Igaz marad-e ekkor is a Galilei-féle relativitás? Idézzük fel, hogy Maxwell elektromágneses hullámai állandó c sebességgel, a fény sebességével terjednek. A józan ész látszólag azt mondja, hogy ha nagyon gyorsan utazunk egy irányban, akkor azt kell látnunk, hogy a fény sebessége abban az irányban c alá csökken (mert úgy mozgunk, hogy abban az irányban utolérjük a fényt), az ellenkező irányban pedig megfelelően c fölé nő (mert eltávolodunk a fénytől) – tehát különbözik a Maxwell-elmélet rögzített értékétől. A józan észnek valóban igaza van: a kombinált Newton- és Maxwell-egyenletek nem elégítik ki a Galilei-féle relativitást.Az ilyen dolgokon való töprengés vezette el 1905-ben Einsteint – mint ahogy valójában előtte (1898 és 1905 között) Poincarét is – a speciális relativitáselmélethez. Poincaré és Einstein egymástól függetlenül azt találták, hogy a Maxwell-egyenletek is kielégítenek egy relativitási elvet (vö. Pais 1982); azaz az egyenletek hasonlóképpen változatlanok maradnak, ha álló vonatkoztatási rendszerről mozgóra térünk át, noha az áttérés szabályai eltérőek a Galilei–Newton-féle fizikára érvényesektől! Hogy a kettő összeférjen egymással, vagy az egyik, vagy a másik egyenletrendszert módosítani kell – vagy elhagyni a relativitási elvet.Einsteinnek nem állt szándékában elhagyni a relativitás elvét. Csodálatos fizikai ösztönével ragaszkodott ahhoz, hogy egy ilyen elvnek érvényesnek kell lennie világunk fizikai törvényeire. Jól tudta továbbá, hogy a Galilei–Newton-féle fizikát tulajdonképpen minden ismert jelenségben csak a fénysebességhez képest nagyon kicsi sebességekre ellenőrizték, ahol az eltérés nem jelentős. Csak magát a fényt ismerték mint olyat, ahol elég nagy sebességek fordulnak elő ahhoz, hogy az eltérések fontosak legyenek. Ezért a fény viselkedése világosíthatna fel bennünket arról, melyik relativitási elvet kell elfogadnunk – a fény viselkedését pedig a Maxwell-egyenletek kormányozzák. Ezért a Maxwell-elméletre érvényes relativitási elvet kell megtartani; a Galilei–Newton-féle törvényeket pedig eszerint kell módosítani!Lorentz, Poincaré és Einstein előtt, szintén felvetette és részben megválaszolta ezeket a kérdéseket. 1895-ben azt a nézetet fogadta el, hogy az anyagot összetartó erők elektromágneses természetűek (ahogy az valóban kiderült), ezért a valóságos anyagi testek viselkedése a Maxwell-egyenletekből származtatott törvényeknek kell eleget tegyen. Ennek egyik következménye az, hogy egy fénysebességhez közeli sebességgel mozgó test a mozgás irányában kismértékben összehúzódik („Fitzgerald–Lorentz-féle kontrakció”). Lorentz ezt egy rejtélyes kísérleti felfedezés magyarázatára használta. Az 1887-es Michelson–Morley-kísérlet volt ez, amely azt látszott mutatni, hogy az elektromágneses jelenségeket nem lehet egy „abszolút” nyugalmi rendszer meghatározására használni. (Michelson és Morley megmutatta, hogy a fény sebességét a Föld felszínén nem befolyásolja a Föld Nap körüli mozgása – nagyon komoly ellentétben a várakozásokkal.) Az anyag mindig úgy viselkedik-e, hogy (egyenletes) mozgását nem lehet lokálisan észlelni? Ez volt Lorentz hozzávetőleges következtetése; ő az anyag egy speciális elméletére korlátozódott, amelyben az elektromágneses erőkön kívül más erőket nem tekintettek lényegesnek. Poincaré, aki kitűnő matematikus volt, meg tudta mutatni (1905-ben), hogy van az anyag viselkedésének egy olyan egzakt, a Maxwell-egyenletek mögött húzódó relativitási elvnek eleget tevő módja, hogy az egyenletes mozgás lokálisan egyáltalán nem észlelhető. Nagyon sokat megértett az elv fizikai következményeiből is (többek között az „egyidejűség viszonylagosságát”, amire rövidesen sort kerítünk). Úgy tetszik, ő ezt csupán egy lehetőségnek tekintette, és nem osztotta Einstein meggyőződését, hogy valamilyen relativitási elvnek érvényesnek kell lennie.A Maxwell-egyenletek által kielégített relativitási elvet – amely speciális relativitás néven vált ismertté – egy kissé nehéz felfogni, és sok olyan nem intuitív vonása van, amelyeket első ránézésre nehéz a mi világunk valóságos tulajdonságainak elfogadni. A speciális relativitást nem lehet megfelelően értelmezni egy további alkotórész nélkül, amelyet 1908-ban vezetett be az igen eredeti és ötletdús orosz-német geométer, Herrmann Minkowski (1864–1909). Einstein egyik tanára volt a Zürichi Műegyetemen. Alapvető új elképzelése az volt, hogy a teret és időt, mint egyetlen dolgot, együtt kell vizsgálni: ez a négydimenziós téridő. 1908-ban a Göttingeni Egyetemen tartott híres előadásán Minkowski kijelentette: Ezentúl az önmagában vett tér és az önmagában vett idő az árnyékvilágban való eltűnésre van ítélve, és csak a kettő egyfajta egyesítése őrzi meg független realitását.Próbáljuk megérteni a speciális relativitás alapjait Minkowski nagyszerű téridőképén keresztül! A téridőfogalommal való megbarátkozás egyik nehézsége az, hogy négydimenziós, ami nehézzé teszi a megjelenítést. Ám miután túléltük találkozásunkat a fázistérrel, a csupán négy dimenzióval már semmi bajunk nem lesz! Mint előbb, most is „csalni” fogunk, és kevesebb dimenziójú teret ábrázolunk – a csalás mértéke azonban most összehasonlíthatatlanul kisebb, képünk ennek megfelelően pontosabb lesz. Két dimenzió (egy térbeli és egy időbeli) sokféle célra elegendő lenne, de remélem, az Olvasó megengedi nekem, hogy kissé merészebb legyek, és felmenjek háromig (két térbeli, egy időbeli). Ez nagyon jó képet fog nyújtani, és nem lesz nehéz elfogadni, hogy az elképzelések nem sok változtatással elvileg kiterjeszthetőek a teljes négydimenziós helyzetre. A téridődiagramról azt kell észben tartanunk, hogy minden pontja egy eseményt ábrázol – azaz egy pontot a térben egyetlen időpontban, egy pontnak ugyanis csak pillanatnyi létezése van. A teljes diagram az egész történetet, múltat, jelent, jövőt ábrázolja. Egy részecskét, mert az időben tovább él, nem pont, hanem vonal ábrázol, amelyet a részecske világvonalának nevezünk. A világvonal a részecske teljes történetét leírja: egyenes, ha a részecske egyenletesen mozog, görbült, ha gyorsul (azaz mozgása nem egyenletes).



Az 5.16. ábrán egy két tér- és egy idődimenziós téridőt rajzoltam le. Képzeljük el, hogy függőleges irányban mérve van egy szabványos t időkoordináta, vízszintesen mérve pedig két térkoordináta, x/c és z/c.90 A középen lévő kúp az O téridő kezdőpont (jövőbe mutató) fénykúpja. Hogy jelentőségét érzékeljük, képzeljünk el egy robbanást az O eseménynél. (A robbanás tehát a térbeli kezdőpontban, a t = 0 időpontban következik be.) A robbanásnál kibocsátott fény története ez a fénykúp. Kétdimenziós térben a fényvillanás története egy c fénysebességgel kifelé mozgó kör volna. A teljes háromdimenziós térben egy c sebességgel kifelé mozgó gömb – a fény gömb alakú hullámfrontja –, de itt most elhagyjuk az y térbeli irányt, így csak egy kört kapunk, hasonlót, mint a tóba dobott kő vízbeérési pontjából kiinduló kör alakú fodrok. A téridőképen is láthatjuk ezt a kört, ha gyorsan mozogva felfelé egymás után vízszintes metszeteket készítünk a kúpból. Ezek a vízszintes síkok különböző térbeli leírásokat ábrázolnak, ahogy a t időkoordináta nő. Na már most, a relativitáselmélet egyik sajátsága az, hogy egy anyagi részecske nem mozoghat gyorsabban a fénynél (erről többet később). A robbanásból jövő minden anyagi részecske le kell maradjon a fény mögött. A téridőképben ez azt jelenti, hogy a robbanásban kibocsátott összes részecske világvonalának a fénykúpon belül kell feküdnie.
A fényt gyakran kényelmes – fotonoknak nevezett – részecskék segítségével leírni. Pillanatnyilag gondolhatunk úgy egy „fotonra”, mint az elektromágneses mező nagyfrekvenciás oszcillációjának egy kis „csomagjára”. A fotonkép fizikailag megfelelőbb a kvantumos leírás összefüggéseiben, erről a következő fejezetben lesz szó, de most a „klasszikus” fotonok is segítségünkre lesznek. A fotonok szabad térben mindig egyenes vonalakon mozognak a c alapsebességgel. Ez azt jelenti, hogy a Minkowski-féle téridőképben egy foton világvonala mindig egy a függőlegessel 45°-os szöget bezáró, egyenes vonal. Az O-ban történt robbanásban keletkezett fotonok rajzolják meg az O középpontú fénykúpot.Ezek a tulajdonságok általánosan, a téridő minden pontjára érvényesek kell legyenek. A kezdőpontot nem tünteti ki semmi: az O pont nem különbözik semelyik másik ponttól. Ezért a téridő minden pontjában kell legyen egy fénykúp, amelynek ugyanaz a jelentése, mint a kezdőpontbeli fénykúpnak. Minden fényfelvillanás története – vagy ha jobban szeretjük a fény részecske leírását, akkor a fotonok világvonalai – mindig minden pontban a fénykúp mentén halad(nak), míg egy anyagi részecske története mindig minden pontban a fénykúpon belül kell legyen. Ezt mutatja az 5.17. ábra. A pontokhoz tartozó fénykúpok családja a téridő Minkowski-geometriája részének tekinthető.
Mi a Minkowski-geometria? Legfontosabb vonása a fénykúpszerkezet, de több annál. Van benne egy „távolság”-fogalom, amely figyelemre méltó hasonlóságokat mutat az euklideszi geometria távolságával. A háromdimenziós euklideszi geometriában egy pontnak a kezdőponttól mért r távolsága, a szokásos derékszögű koordinátákkal kifejezve, a következő:
r2 = x2 + y2 + z2. (Lásd 5.18a. ábra. Ez éppen a Pitagorasz-tétel – kétdimenziós alakja talán jobban megszokott.) Háromdimenziós Minkowski-geometriánkban a kifejezés formailag nagyon hasonló (5.18b. ábra), a lényeges különbség az, hogy most két mínuszjel van benne: s2 = t2 – (x/c)2 – (z/c)2. Helyesebben szólva, Minkowski-geometriánk természetesen négydimenziós, és a „távolság” kifejezése a következő: s2 = t2 – (x/c)2 – (y/c)2 – (z/c)2. Mi a fizikai jelentése az s „távolság”-mennyiségnek ebben a kifejezésben? Tegyük fel, hogy a kérdéses pont – azaz a {t, x/c, y/c, z/c} (vagy a háromdimenziós esetben a {t, x/c, z/c}) koordinátákkal adott P pont – O (jövőbe mutató) fénykúpján belül fekszik. Ekkor az OP egyenes szakasz egy anyagi részecske – mondjuk a robbanásban keletkező valamelyik részecske – történetének egy szakaszát ábrázolhatja. Az OP szakasz s Minkowski-„hosszának” közvetlen fizikai értelmezése van. Ez az az időtartam, amelyet a részecske valójában átélt az O és P események között! Azaz ha volna egy, a részecskéhez rögzített, nagyon tartós és pontos óra,91 akkor az O-ban és P-ben észlelt idők közötti különbség pontosan s volna. A várakozásokkal ellentétben maga a t koordináta mennyiség nem adja meg a pontos óra által mért időt, hacsak az nincs koordináta-rendszerünkben „nyugalomban” (azaz x/c, y/c, z/c koordinátái rögzítettek), ami azt jelenti, hogy az óra világvonala a diagramon „függőleges”. Így „t” csak a nyugalomban lévő (azaz „függőleges” világvonalú) megfigyelők számára jelent „időt”. Mozgó (az O kezdőponttól egyenletesen távolodó) megfigyelőnél az idő helyes mértékét a speciális relativitáselmélet szerint az s mennyiség adja.Ez nagyon figyelemreméltó – és teljesen eltér az idő „hétköznapi”, Galilei–Newton-féle mértékétől, ami egyszerűen a t koordinátaérték volna. Jegyezzük meg, hogy az s relativisztikus (Minkowski-féle) időmérték valamivel mindig kisebb, mint t, ha egyáltalán van mozgás (mert a fenti képlet szerint s2 kisebb, mint t2, amikor csak x/c, y/c és z/c nem mind nulla). A mozgás (azaz, ha OP nincs a t tengely mentén) „lelassítja” az órát t-hez képest, azaz koordinátarendszerünkből nézve. Ha a mozgás sebessége c-hez képest kicsi, akkor s és t majdnem azonos, ami megmagyarázza, miért nem vagyunk közvetlenül tudatában annak, hogy „a mozgó órák késnek”. A másik szélsőséges esetben, amikor a sebesség maga a fénysebesség, P a fénykúpon fekszik; és azt találjuk, hogy s = 0. A fénykúp pontosan azon pontok halmaza, amelyeknek O-tól mért „Minkowski-távolsága” (azaz „ideje”) éppen nulla. Így egy foton egyáltalán nem „tapasztalja” az idő múlását! (A még szélsőségesebb eset, amikor P a kúpon kívülre esik, nincs megengedve, mert ez képzetes s-hez vezetne – negatív szám négyzetgyöke képzetes – és sértené azt a szabályt, hogy anyagi részecskék vagy fotonok nem mozoghatnak gyorsabban, mint a fény.92)A Minkowski-féle „távolság”-fogalom egyformán jól alkalmazható a téridő „bármely” pontpárjára, amelyeknél az egyik a másik fénykúpjában fekszik – vagyis egy részecske elmehetne az egyikből a másikba. Helyezzük át O-t a téridő egy másik pontjába. A pontok közötti Minkowski-távolság ismét azt az időtartamot méri, amelyet az egyikből a másikba egyenletesen mozgó óra tapasztal. Ha megengedjük, hogy a részecske foton legyen, és így a Minkowski-távolság zérussá váljon, akkor két olyan pontot kapunk, amelyek közül az egyik rajta van a másik fénykúpján – ez a körülmény szolgál egy pont fénykúpjának definiálására.A Minkowski-geometria alapvető szerkezete a „hossz” e furcsa mértékével a világvonalakon – amit a fizikai órák által mért (vagy „tapasztalt”) időként értelmezünk – tartalmazza a speciális relativitáselmélet igazi lényegét. Megismerkedhet az Olvasó például a relativitás ún. ikerparadoxonával: egy ikerpár egyik tagja a Földön marad, a másik kirándulást tesz egy közeli csillagra, a fénysebességet megközelítő nagy sebességgel utazik oda és vissza. Visszaérkezésekor az ikrek úgy találják, hogy különbözőképpen öregedtek meg, az utazó még életerős ifjú, míg otthon maradt testvére öregember. A Minkowski-geometria segítségével ez könnyen leírható – és látható, hogy bár a jelenség rejtélyes, valójában miért nem paradoxon. Az AC világvonal az otthon maradó ikret ábrázolja, míg az utazó világvonala az AB és BC szakaszokból tevődik össze, ezek ábrázolják az utazás odafelé és visszafelé tartó részét (lásd 5.19. ábra). Az otthon maradó iker az AC Minkowski-távolsággal mért idő elmúlását tapasztalja, míg az utazó a két Minkowski-távolság, AB és BC összegével93 adott időét. Ezek az idők nem egyenlőek, azt találjuk, hogy AC > AB + BC, AC < AB + BC, ami azt állítja, hogy egy háromszög két oldalának összege mindig nagyobb, mint a harmadik. Ezt nem tekintjük paradoxonnak! Ahhoz teljesen hozzászoktunk, hogy egy út mentén két pont (most A és C) közötti távolság euklideszi mértéke a valóságosan megtett úttól függ. (Esetünkben az egyik AC, a hosszabb, megtört út ABC.) Ez a példa speciális esete annak a ténynek, hogy két pont (most A és C) között a legrövidebb távolságot az őket összekötő egyenes vonal (az AC vonal) mentén mérjük. Az egyenlőtlenség irányának megfordulása a Minkowski-esetben a „távolság” definíciójában fellépő előjelváltásból származik, ezért a Minkowski-féle AC „hosszabb”, mint az ABC egyesített út. E Minkowski-féle „háromszög-egyenlőtlenség” is egy általánosabb eredmény speciális példája: két eseményt összekötő világvonalak között a leghosszabb (a legnagyobb észlelt idő értelmében) az egyenes (azaz a gyorsulás nélküli). Ha két iker ugyanattól az A eseménytől indul és ugyanannál a C eseménynél fejezi be útját, közben az első közvetlenül, gyorsulás nélkül mozog A-tól C-ig, a másik viszont gyorsul, akkor az első mindig hosszabb idő elteltét tapasztalja, amikor újra találkoznak.ami mutatja, hogy az otthon maradó által tapasztalt idő nagyobb, mint az utazó által megélt.
Erőszakoltnak tűnhet, hogy intuitív fogalmainktól eltérően ilyen különös időmérést vezetünk be. Mára azonban már nagy mennyiségű kísérleti bizonyíték gyűlt össze ennek alátámasztására. Van például sok szubatomi részecske, amelyek bomlásainak (azaz más részecskékre való széteséseinek) ideje meghatározott. Ezek a részecskék olykor a fénysebességhez nagyon közeli sebességgel mozognak (például a kozmikus sugarakban, amelyek a világűrből érkeznek a Földre, vagy az ember készítette részecskegyorsítókban) és bomlásidejük pontosan úgy növekszik meg, ahogy azt a fenti meggondolásokból levezethetjük. Még meggyőzőbb az a tény, hogy ma már olyan pontos órák („nukleáris órák”) készíthetők, hogy ezek az időlassító hatások közvetlenül észlelhetők gyors, alacsonyan szálló repülőkön vitt órák segítségével – ezek a Minkowski-féle s „távolság”-mértéket erősítik meg és nem t-t! (Figyelembe véve a repülőgép magasságát, szigorúan számítva az általános relativitáselmélet kis, járulékos gravitációs hatásai is közbeszólnak, de ezek is egyeznek a megfigyeléssel; lásd a következő fejezetet.) Van még sok más, a speciális relativitás egész szerkezetével szoros kapcsolatban álló jelenség, amelyek folyamatosan részletes igazolást nyernek. Ezek egyikének, Einstein híres E = mc2 összefüggésének, amely hatásosan fejezi ki az energia és a tömeg egyenértékűségét, e fejezet vége felé tantaluszi kínokat okozó következményei lesznek számunkra!
Nem magyaráztam még el, hogyan illeszkedik be a relativitás elve a dolgoknak ebbe a rendjébe. Hogyan van az, hogy a különböző nagyságú, egyenletes sebességgel mozgó megfigyelők a Minkowski-geometriát illetően egyenértékűek lehetnek? Hogyan lehet az 5.16. ábra időtengelye („nyugvó megfigyelő”) teljesen egyenértékű egy másik egyenes világvonallal, mondjuk a meghosszabbított OP-vel („mozgó megfigyelő”)? Gondoljunk először az euklideszi geometriára. Bármely két egyenes vonal nyilvánvalóan teljesen egyenértékű egymással a geometria mint egész szempontjából. Elképzelhetjük, hogy az egész euklideszi teret „önmaga fölött mereven elcsúsztatjuk” addig, amíg az egyik egyenes a másik helyzetét veszi fel. Gondoljunk a kétdimenziós esetre, az euklideszi síkra. Képzeljük el, hogy egy darab papírt mozgatunk mereven egy síkfelületen úgy, hogy a papírra rajzolt tetszőleges egyenes vonal egybeesik a felület egy adott egyenes vonalával. Ez a merev mozgás megőrzi a geometria szerkezetét. Bár kevésbé nyilvánvalóan, de valami hasonló érvényes a Minkowski-geometriára, óvatosan kell viszont bánni a „merev” szóval. A csúsztatott papírdarab helyébe most egy sajátos anyagot kell gondolnunk – az egyszerűség kedvéért vegyük először a kétdimenziós esetet –, amelyben a 45°-os vonalak 45°-osak maradnak, az anyag ki tud nyúlni az egyik 45°-os irányban és megfelelően összehúzódni a másikban. Ezt mutatja az 5.20. ábra. Az 5.21. ábrán megpróbáltam érzékeltetni, mi történik a háromdimenziós esetben. A Minkowski-térnek ez a fajta „merev mozgása” – amelyet Poincaré-mozgásnak (vagy inhomogén Lorentz-mozgásnak) hívnak –, bár nem néz ki nagyon „merevnek”, de megőriz minden Minkowski-távolságot, és „megőrizni minden távolságot”, éppen ez az, amit a „merev” szó az euklideszi esetben jelent. A speciális relativitás elve azt állítja, hogy a fizika a téridő ilyen Poincaré-mozgásai során nem változik. Speciálisan az N „nyugvó” megfigyelő, akinek világvonala az 5.16. ábrán látható eredeti Minkowski-képünk időtengelye, tökéletesen egyenértékű fizikát lát az OP világvonalú M „mozgó” megfigyelő fizikájával.Minden t = állandó koordinátasík a „teret” ábrázolja egy „időpontban” az N megfigyelő számára, azaz események egy családját, amelyeket ő egyidejűnek (azaz mindegyiket „azonos időpontban” bekövetkezőnek) tekint. Nevezzük ezeket a síkokat N egyidejű tereinek. Amikor áttérünk egy másik M megfigyelőhöz, akkor egyidejű tereink eredeti családját egy új családba kell Poincaré-mozgással átvinnünk, hogy megkapjuk az M számára egyidejű tereket.94 Vegyük észre, hogy M egyidejű terei az 5.21. ábrán „felbillenteknek” látszanak. Ez a billenés rossz irányúnak tűnhet, ha az euklideszi geometria merev mozgásaiban gondolkodunk, de a Minkowski-esetben ezt kell várnunk. Amíg N azt gondolja, hogy tetszőleges t = állandó síkon minden esemény egy időben következik be, addig M másként látja a dolgokat: számára az ezekben a „felbillent” egyidejű terekben bekövetkező események látszanak egyidejűeknek! A Minkowski-geometriában önmagában nincs általános „egyidejűség” fogalom; minden egyenletesen mozgó megfigyelőnek saját elképzelése van arról, mit jelent az, hogy „egyidejű”.Tekintsük az 5.21. ábra két eseményét, R-et és Q-t. N szerint az R esemény megelőzi a Q-t, mert R korábbi egyidejű térben fekszik, mint Q; M szerint azonban más a helyzet, Q fekszik R-nél korábbi egyidejű térben. Így az egyik megfigyelő számára az R esemény megelőzi a Q-t, de a másik számára a Q előzi meg az R-et! (Ez csak azért történhet meg, mert R és Q térszerűen elválasztottak, ami azt jelenti, hogy mindkettő a másik fénykúpján kívül fekszik, anyagi részecske vagy foton nem utazhat át egyik eseménytől a másikig.) Nagy távolságra lévő eseményeknél, még egészen csekély relatív sebességek mellett is, jelentős különbségek lépnek fel az időrendezésben. Képzeljünk el két embert, amint lassan elsétálnak az utcán egymás mellett. Azok az Androméda-galaxisban (a Tejutunkhoz legközelebbi nagy galaxisban, kb. 20 000 000 000 000 000 000 km távolságban) lezajló események, amelyeket a két ember egymás melletti elhaladásukkal egyidejűnek ítél meg, több napnyi különbséget is mutathatnak (5.22. ábra). Az egyik ember szerint az űrhajó, amely azzal a szándékkal indul, hogy a Földön megsemmisítse az életet, már úton van; míg a másik szerint még a döntés sem született meg arról, hogy elindítsák-e az űrhajót vagy sem
Az 5.16. ábrán egy két tér- és egy idődimenziós téridőt rajzoltam le. Képzeljük el, hogy függőleges irányban mérve van egy szabványos t időkoordináta, vízszintesen mérve pedig két térkoordináta, x/c és z/c.90 A középen lévő kúp az O téridő kezdőpont (jövőbe mutató) fénykúpja. Hogy jelentőségét érzékeljük, képzeljünk el egy robbanást az O eseménynél. (A robbanás tehát a térbeli kezdőpontban, a t = 0 időpontban következik be.) A robbanásnál kibocsátott fény története ez a fénykúp. Kétdimenziós térben a fényvillanás története egy c fénysebességgel kifelé mozgó kör volna. A teljes háromdimenziós térben egy c sebességgel kifelé mozgó gömb – a fény gömb alakú hullámfrontja –, de itt most elhagyjuk az y térbeli irányt, így csak egy kört kapunk, hasonlót, mint a tóba dobott kő vízbeérési pontjából kiinduló kör alakú fodrok. A téridőképen is láthatjuk ezt a kört, ha gyorsan mozogva felfelé egymás után vízszintes metszeteket készítünk a kúpból. Ezek a vízszintes síkok különböző térbeli leírásokat ábrázolnak, ahogy a t időkoordináta nő. Na már most, a relativitáselmélet egyik sajátsága az, hogy egy anyagi részecske nem mozoghat gyorsabban a fénynél (erről többet később). A robbanásból jövő minden anyagi részecske le kell maradjon a fény mögött. A téridőképben ez azt jelenti, hogy a robbanásban kibocsátott összes részecske világvonalának a fénykúpon belül kell feküdnie.
Mi a Minkowski-geometria? Legfontosabb vonása a fénykúpszerkezet, de több annál. Van benne egy „távolság”-fogalom, amely figyelemre méltó hasonlóságokat mutat az euklideszi geometria távolságával. A háromdimenziós euklideszi geometriában egy pontnak a kezdőponttól mért r távolsága, a szokásos derékszögű koordinátákkal kifejezve, a következő:
Tekintsük az 5.21. ábra két eseményét, R-et és Q-t. N szerint az R esemény megelőzi a Q-t, mert R korábbi egyidejű térben fekszik, mint Q; M szerint azonban más a helyzet, Q fekszik R-nél korábbi egyidejű térben. Így az egyik megfigyelő számára az R esemény megelőzi a Q-t, de a másik számára a Q előzi meg az R-et! (Ez csak azért történhet meg, mert R és Q térszerűen elválasztottak, ami azt jelenti, hogy mindkettő a másik fénykúpján kívül fekszik, anyagi részecske vagy foton nem utazhat át egyik eseménytől a másikig.) Nagy távolságra lévő eseményeknél, még egészen csekély relatív sebességek mellett is, jelentős különbségek lépnek fel az időrendezésben. Képzeljünk el két embert, amint lassan elsétálnak az utcán egymás mellett. Azok az Androméda-galaxisban (a Tejutunkhoz legközelebbi nagy galaxisban, kb. 20 000 000 000 000 000 000 km távolságban) lezajló események, amelyeket a két ember egymás melletti elhaladásukkal egyidejűnek ítél meg, több napnyi különbséget is mutathatnak (5.22. ábra). Az egyik ember szerint az űrhajó, amely azzal a szándékkal indul, hogy a Földön megsemmisítse az életet, már úton van; míg a másik szerint még a döntés sem született meg arról, hogy elindítsák-e az űrhajót vagy sem
Einstein általános relativitás elmélete
Galilei meglátása: gravitációs mezőben minden test egyenlő gyorsan esik. (Galilei azt ismerte fel, hogy ha a levegő ellenállását nullára lehetne csökkenteni, akkor egyformán esnének.) Három évszázad telt el, míg e meglátás mély jelentőségét igazán felismerték és sarokkőként illlesztették be egy nagy elméletbe.Ez az elmélet Einstein általános relativitás elmélete-Az elmélet megalkotásához szükséges fogalom:
a görbült téridő , annak elképzelése....valóban igaz lehet-e, hogy Galilei régi meglátása tartalmazott valamit ami Newton elméletébe nincs beépítve? ...Mi szabja meg a gravitáció hatása alatt álló test gyorsulását?...Először van a testre ható erő, amelyről a gravitációs vonzás Newtom-törvénye azt mondja:...arányos a test tömegével. Másodszor: adott erő mellett a test gyorsulása fordítva arányos a test tömegével. Galilei meglátása azon a tényen alapul, hogy a Newton-féle gravitációs erőtörvényben szereplő "tömeg" ugyanaz, mint a Newton második törvé-nyében szerplő "tömeg".(Az azonosság helyett elegendő az arányosság.) Ez biztosítja, hogy a gravitáció hatására a test gyorsulása valóban független a tömegétől. Newton általános rendszerében semmi olyan nincs, ami megkövetelte volna, hogy ez a két tömegfogalom azonos legyen. Ezt Newton egyszerűen posztulálta. Az elektromos erők hasonlóak a gravitációsokhoz annyiban, hogy mindkettő inverz négyzetes erő, de előbbiek az elektromos töltéstől függnek, ami teljesen más, mint a Newton második törvényében szereplő tömeg."Galilei meglátása" az elekttromos erőkre nem alkalmazható: elektromos mezőben "elejtett" (töltött) tárgyak egyáltalán nem azonos sebességgel "esnek"!Most egyelőre egyszerűen fogadjuk el Galilei meglátását – a gravitációs mozgásra –, és keressük annak következményeit. Az űrrepülés ma az elképzelések jobb ellenőrzését kínálja, mert a világűrben valóban nincs levegő. Ott az „esés” a megfelelő gravitációs pályán való mozgást jelenti. Nem kell, hogy ez az „esés” lefelé, a Föld középpontja felé irányuljon. A mozgásnak vízszintes összetevője is lehet. Ha ez a vízszintes összetevő elég nagy, akkor lehet úgy „esni” a Föld körül, hogy a talajhoz semmivel nem jutunk közelebb! Gravitáció hatására szabad pályán mozogni, az „esés” egy finom (és nagyon drága!) módja. .... egy „űrsétát” végző űrhajós járművét úgy látja, hogy az előtte lebeg, az alatta lévő hatalmas Földgolyó gravitációs erejétől nem befolyásolva! (Lásd az 5.24. ábrát a könyvben) Így a gravitáció hatásait lokálisan ki lehet küszöbölni oly módon, hogy áttérünk a szabadesés „gyorsuló vonatkoztatási rendszerére”. ...A gravitáció a szabadeséssel ily módon kioltható, mert a gravitációs mező hatásai éppen olyanok, mint a gyorsulásé. Valóban, a felfelé gyorsuló lift belsejében a gravitációs mező növekedését érezzük, a lefelé gyorsulóban csökkenését. Ha a liftet tartó kötél elszakadna, akkor (a légellenállást és a súrlódást elhanyagolva) a létrejövő lefelé irányuló gyorsulás teljesen megszüntetné a gravitáció hatását, és a lift utasai – mint előbb az űrhajós – szabadon lebegnének, míg a lift be nem csapódna a földbe! A gyorsulás még egy vonatban vagy repülőgépen is lehet olyan, hogy a gravitáció nagyságát és irányát nem úgy érezzük, mint ahogy vizuális tapasztalatunk sugallná. Ez azért van így, mert a gyorsulás és a gravitáció hatásai hasonlóak, ezért érzékeink képtelenek azokat megkülönböztetni egymástól. Ezt a tényt – hogy a gravitáció lokális hatásai egyenértékűek egy gyorsuló vonatkoztatási rendszeréivel – Einstein az ekvivalencia elvének nevezte. ...A fenti megfontolások „lokálisak”. Ám ha elegendően pontos (és nem egészen lokális) méréseket tudunk végezni, akkor elvileg kideríthetünk egy különbséget az „igazi” gravitációs mező és az egyszerű gyorsulás között. Az 5.25. ábrán kissé eltúlozva azt mutatom be, hogyan kezdené befolyásolni a (newtoni) gravitációs mező nemegyenletessége a Föld gravitációs mezőjében szabadon eső részecskék kezdeti stacionárius, gömbszimmetrikus elrendezését. A mező két okból nem egyenletes. Először azért, mert a Föld középpontja véges távolságban van, a Föld felszínéhez közelebbi részecskék jobban gyorsulnak lefelé, mint azok, amelyek magasabban vannak (emlékezzünk Newton inverz négyzetes törvényére). Másodszor azért, mert ugyanezen okból a gyorsulás irányában is lesznek csekély különbségek a vízszintesen eltérő helyzetű részecskéknél. E nemegyenletesség következtében a gömbalak kissé torzulni kezd: egy „ellipszoidba”. A Föld középpontjának irányában (és az ellentétes irányban) megnyúlik, mert a középponthoz közelebbi részecskék valamivel nagyobb gyorsulást tapasztalnak, mint a távolabbiak; vízszintes irányban összehúzódik annak következtében, hogy a gyorsulás egy kissé befelé, a Föld középpontjának irányába mutat.
Ez a torzító hatás úgy ismert, mint a gravitáció árapályjelensége. Ha a Föld középpontját a Holddal, a részecskegömböt pedig a Föld felületével helyettesítjük, akkor pontosan előttünk áll a Hold árapályt előidéző hatása, mind a Hold irányában, mind az ellentétes irányban kidagadás jön létre. Az árapályjelenség a gravitációs mezőknek általános tulajdonsága, amelyet szabadeséssel nem lehet „kioltani”. Ez a jelenség a newtoni gravitációs mező nemegyenletességét méri. (Az árapálytorzítás nagysága a vonzócentrumtól mért távolság inverz köbe és nem inverz négyzete szerint csökken.)Newton inverz négyzetes erőtörvényét az árapályjelenség segítségével egyszerűen lehet értelmezni: annak az ellipszoidnak a térfogata, amellyé a gömb kezdetben95 torzul, egyenlő az eredeti gömb térfogatával – ha a gömb vákuumot vesz körül. Ez a térfogat-tulajdonság az inverz négyzetes törvényre jellemző; más erőtörvényre nem érvényes. Tegyük most fel, hogy a gömb nem vákuumot, hanem M össztömegű anyagot vesz körül. Az anyag gravitációs vonzásának következtében a gyorsulásnak most lesz egy további, befelé mutató összetevője. Az ellipszoid térfogata, amelybe részecskegömbünk kezdetben átmegy, összehúzódik – M-mel arányos mértékben. Egy példa a térfogatcsökkentő hatásra, ha gömbünkkel a Földet vesszük körbe állandó magasságban (5.26. ábra). Ekkor a Föld gravitációja által okozott, szokásos lefelé (azaz befelé) mutató gyorsulás okozza gömbünk térfogatának csökkenését. Ez a térfogatcsökkentő tulajdonság szabja meg Newton gravitációs erőtörvényének maradék részét, nevezetesen azt, hogy az erő arányos a vonzó test tömegével. Próbáljunk téridőképet készíteni a helyzetről! Az 5.27. ábrán (az 5.25. ábrán körrel ábrázolt) gömbfelületünk részecskéinek világvonalait tüntettem fel, a leírást abban a rendszerben végzem, amelyben a gömb középpontja nyugalomban van („szabadon esik”). Az általános relativitáselmélet a szabadesést „természetes mozgásnak” tekinti – a gravitációmentes fizika „egyenes vonalú, egyenletes mozgásának” mintájára. Ezért úgy próbálunk gondolni a szabadesésre, mint amelyet „egyenes” világvonal ír le a téridőben! Ám az 5.27. ábra tanúsága szerint zavaró az „egyenes” szó használata, és a terminológiát követve a szabadon eső részecskék világvonalait a téridő geodetikusainak fogjuk nevezni.Jó-e ez a terminológia? Mit értünk rendesen „geodetikuson”? Vizsgáljunk meg egy hasonló helyzetet egy kétdimenziós görbült felületen. A geodetikusok azok a görbék a felületen, amelyek (lokálisan) a „legrövidebb utak”. Ha gondolatban egy rugót húzunk ki a felületen (nem túl hosszút, mert akkor elcsúszhat), akkor az a felület egy geodetikusa mentén fog elhelyezkedni. Az 5.28. ábrán két példát mutatok a felületekre, az elsőt „pozitív görbületűnek” nevezik (a gömb felületéhez hasonló), a második „negatív görbületű” (nyeregszerű felület). A pozitív görbületű felületen két szomszédos geodetikus, amelyek egymással párhuzamosan indulnak, egymás felé kezdenek hajlani; a negatív görbületűn egymástól széthajlanak. Ha elképzeljük, hogy a szabadon eső részecskék világvonalai valamilyen értelemben olyanok, mint egy felület geodetikusai, akkor látjuk, hogy közeli a hasonlóság az előbb tárgyalt gravitációs árapályjelenség és egy felület görbületi hatásai között – most azonban a pozitív és negatív görbületi hatások egyaránt jelen vannak. Nézzünk az 5.25. és 5.27. ábrákra. Látjuk, hogy téridő-„geodetikusaink” az egyik irányban kezdenek szétválni egymástól (amikor a Föld irányába haladnak) – mint a negatív görbületű felületen az 5.28. ábrán –, a másik irányban egymás felé kezdenek hajlani – mint az 5.28. ábra pozitív görbületű felületén. Valóban úgy látszik, hogy téridőnknek „görbülete” van, hasonlóan kétféle felületünkhöz, de a magasabb dimenzió miatt azoknál bonyolultabb, és különböző elmozdulásoknál pozitív és negatív görbületek összekeveredve jelentkeznek. Ez mutatja, hogyan használható a „görbület” fogalma a téridőben a gravitációs mezők hatásának leírására. Az ilyen leírás használatának lehetősége végül is Galilei meglátásából (az ekvivalencia elvéből) következik, és megengedi, hogy a szabadeséssel kiküszöböljük a gravitációs „erőt”. Amit eddig mondtam, az nem követeli meg, hogy túlmenjünk Newton elméletén. Az új kép csak átfogalmazása az elméletnek.96 Új fizika keletkezik azonban, amikor ezt a képet megpróbáljuk összekombinálni azzal, amit megtanultunk a speciális relativitás Minkowski-féle leírásából – a téridő geometriájából, amelyről már tudjuk, hogy gravitáció hiányában alkalmazható. A kombináció eredménye Einstein általános relativitáselmélete. Minkowski geometriáját egzaktnak vesszük, ha nincs gravitációs mező – azaz nincs téridőgörbület. Amikor azonban gravitáció van jelen, akkor a Minkowski-geometriát csak közelítőnek tekintjük – ugyanúgy, ahogy egy sima felület csak közelítő leírását adja egy görbült felület geometriájának. Ha elképzeljük, hogy egyre erősebb mikroszkóppal vizsgálunk egy görbült felületet – ekkor a felület geometriája egyre nagyobb mértékben látszik megnyújtottnak –, akkor a felület egyre simábbnak látszik. Azt mondjuk, hogy egy görbült felület lokálisan olyan, mint egy euklideszi sík.97 Ugyanígy azt mondhatjuk, hogy gravitáció jelenlétében a téridő lokálisan Minkowski-geometriához hasonló (ami sima téridő), de nagyobb skálán megengedünk bizonyos „görbültséget” (lásd az 5.29. ábrát). A téridő minden pontja egy fénykúp csúcsa, éppen úgy, mint a Minkowski-térben, de ezek a fénykúpok nem teljesen egyformán állnak, nem olyan egyenletesen, mint a Minkowski-térben. A 7. fejezetben látni fogjuk a téridőmodellek néhány példáját, amelyekben ez a nemegyenletesség szemmel látható (vö. a 7.13., 7.14. ábrákat). Az anyagi részecskék világvonalai olyan görbék, amelyek mindig a fénykúpok belsejében haladnak, a fotonok görbéi a fénykúpok mentén. Bármelyik görbe mentén van „Minkowski-távolság”, amely a részecskék által átélt időt méri éppúgy, mint a Minkowski-térben. E távolságmérték a görbült felületekhez hasonlóan egy geometriát definiál a felületen, amely különbözhet a sík geometriájától.A téridő-geodetikusoknak most hasonló értelmezés adható, mint a kétdimenziós felületek előbb vizsgált geodetikusainak, de nem szabad elfelejtkeznünk a Minkowski- és euklideszi helyzetek különbségeiről. Így geodetikus világvonalaink a téridőben nem (lokálisan) minimális hosszúságú görbék, hanem olyanok, amelyek (lokálisan) maximálják a „távolságot” (azaz időt) a világvonal mentén. A gravitáció hatására szabad mozgást végző részecskék világvonalai e szabály szerint valóban geodetikusok. Így speciálisan e geodetikusok jól leírják a gravitációs mezőben mozgó égitesteket. Továbbmenve: az üres térben a fénysugarak (a fotonok világvonalai) szintén geodetikusok, de ezek zérus „hosszúságúak”.98 Példaként az 5.30. ábrán vázlatosan felrajzoltam a Föld és a Nap világvonalait: a Föld Nap körüli mozgása egy „dugóhúzó”-szerű geodetikus a Nap világvonala körül. Bejelöltem egy fotont is, amely egy távoli csillagból jut a Földre. Ennek világvonala kissé „íveltnek” látszik annak következtében, hogy a fényt Einstein elmélete szerint a Nap gravitációs mezője elhajlítja.
A négydimenziós téridő görbületének teljes matematikai kifejezését (amelynek egy adott pontban minden lehetséges irányban mozgó részecskékre le kell írnia az árapályjelenséget) az ún. Riemann-féle görbületi tenzor adja meg. Ez eléggé bonyolult valami, megadásához minden pontban húsz valós szám szükséges. Ezt a húsz számot a tenzor komponenseinek nevezzük. A különböző komponensek a téridő különböző irányainak különböző görbületeire vonatkoznak. A Riemann-féle görbületi tenzorra rendszerint az Rijkl jelölést használják, de az egyszerűség kedvéért azt fogom írni, hogy RIEMANN. E tenzort egy bizonyos módon két részre lehet bontani, Weyl-tenzornak nevezik az egyik részt, Ricci-tenzornak a másikat (mindkettőnek tíz komponense van). E szétbontást jelképesen így fogom írni: RIEMANN = WEYL + RICCI. (A részletes kifejezések különösebben nem segítenének bennünket.) A WEYL Weyl-tenzor szabadon eső részecskegömbünk árapálytorzítását méri (a kezdeti alakváltozást és nem a méretváltozást), a RICCI Ricci-tenzor pedig a kezdeti térfogatváltozást.99 Emlékezzünk vissza, hogy a newtoni gravitációs elmélet szerint az eső gömb által körülvett tömeg arányos e kezdeti térfogatcsökkenéssel. Ez durván szólva azt mondja nekünk, hogy az anyag tömegsűrűségét – vagy ami ezzel egyenértékű, energiasűrűségét (mert E = mc2) – a Ricci-tenzorral kell egyenlővé tenni.Alapvetően ennyit állítanak az általános relativitáselmélet mezőegyenletei – nevezetesen az Einstein-féle mezőegyenletek.100 Vannak azonban ezzel kapcsolatban bizonyos technikai dolgok, amelyeket most jobb nem firtatni. Elég lesz annyi, hogy van egy energia-impulzus tenzornak nevezett mennyiség, amely összefogja az anyag és az elektromágneses mezők energiájára, nyomására és impulzusára vonatkozó összes lényeges információt. Ezt a tenzort úgy fogom jelölni, hogy ENERGIA. Az Einstein-egyenletek nagyon formálisan a RICCI = ENERGIA alakban írhatók. (A „nyomás” jelenléte az ENERGIA tenzorban, valamint az egész egyenletrendszerre vonatkozó konzisztenciakövetelmények – ezek együttes következménye, hogy a nyomás szintén hozzájárul az előbb leírt térfogatcsökkentő hatáshoz.)Az egyenlet, úgy látszik, semmit nem mond a Weyl-tenzorról. Ez azonban fontos mennyiség. Az üres térben tapasztalt árapályjelenség teljesen a WEYL következménye. A fenti Einstein-egyenletek valójában maguk után vonják, hogy vannak differenciálegyenletek, amelyek a WEYL-t kötik össze az ENERGIÁ-val, eléggé hasonlóak, mint a korábban megismert Maxwell-egyenletek.101 Valóban gyümölcsöző nézőpont úgy tekinteni WEYL-t, mint az (E, B) párral leírt elektromágneses mezőmennyiségek egyfajta gravitációs analogonját (ténylegesen ezek is tenzort alkotnak – a Maxwell-tenzort). Így bizonyos értelemben WEYL a gravitációs mezőt méri. A WEYL „forrása” az ENERGIA tenzor, ami analóg azzal, hogy az (E, B) elektromágneses mező forrása (ρ, j), tehát a Maxwell-elmélet töltései és áramai. Ez a nézőpont segítségünkre lesz a 7. fejezetben.Ha a megfogalmazás és az alapul szolgáló ideák ilyen meglepő különbségeire gondolunk, akkor figyelemre méltó lehet, hogy nehéz megfigyelhető különbségeket találni az Einstein-elmélet és ama másik között, amelyet Newton állított fel két és fél évszázaddal korábban. Feltéve azonban, hogy a szóban forgó sebességek a fény c sebességéhez képest kicsik, és hogy a gravitációs mezők nem túl erősek (a szökési sebességek sokkal kisebbek, mint c; vö. 7. fejezet), az Einstein-elmélet a Newtonéval tulajdonképpen azonos eredményeket ad. Ám azokban az esetekben, amelyekben a két elmélet jóslatai különböznek, az Einstein-elmélet a pontosabb. Ma már van néhány ilyen, nagyon meggyőző kísérleti ellenőrzés, amelyek teljesen igazolják Einstein modernebb elméletét. Az órák gravitációs mezőben, ahogy Einstein állította, nagyon picit késnek. Ezt a jelenséget mára már sok különböző módon közvetlenül megmérték. A Nap valóban eltéríti a fényt és a rádiójeleket, és e találkozás kissé lelassítja azokat – ezek is jól ellenőrzött hatásai az általános relativitásnak. Az űrszondák és bolygók mozgásában a newtoni pályákhoz kis korrekciók járulnak, amint azt Einstein elmélete megköveteli; kísérletileg ezt is igazolták. (A Merkur bolygó mozgásában fellelhető, „perihéliumelfordulás” néven ismert anomáliát, amely a csillagászokat 1859 óta foglalkoztatja, Einstein 1915-ben megmagyarázta.) Mind közül talán a legmeggyőzőbb a két kicsi, nagy tömegű csillagból (feltehetően „neutroncsillagokból”, vö. 7. fejezet) álló, kettős pulzárnak nevezett rendszeren végzett megfigyeléssorozat, amely nagyon jól egyezik Einstein elméletével, és közvetett módon igazol egy olyan jelenséget, a gravitációs hullámok kibocsátását, amely Newton elméletéből teljesen hiányzik. (A gravitációs hullám az elektromágneses hullám gravitációs analogonja, amely a fény c sebességével terjed.) Nincs olyan megerősített megfigyelés, amely ellentmond Einstein általános relativitáselméletének. Minden kezdeti furcsasága ellenére Einstein elmélete határozottan a mi kincsünk!
Relativisztikus kauzalitás és determinizmus
Emlékezzünk arra, hogy a relativitáselméletben az anyagi testek nem mozoghatnak a fénynél gyorsabban – abban az értelemben, hogy világvonalaiknak mindig a fénykúpokon belül kell haladniuk (vö. 5.29. ábra). (Az általános relativitáselméletben a dolgokat ilyen lokális módon kell megfogalmaznunk. A fénykúpok nem rendeződnek el egyenletesen, így nem volna sok értelme azt mondani, hogy egy nagyon távoli részecske sebessége felülmúlja-e az itteni fénysebességet.) A fotonok világvonalai a fénykúpok mentén fekszenek, de semmilyen részecske világvonala nem haladhat a kúpokon kívül. Valójában egy általánosabb állításnak kell igaznak lennie, nevezetesen annak, hogy semmilyen jel nem mehet a fénykúpon kívül.
Hogy megértsük, miért kell ennek így lennie, nézzük meg a Minkowski-térről rajzolt képeket (5.31. ábra). Tegyük fel, hogy készítettünk egy eszközt, amely a fényénél kicsit nagyobb sebességű jelet képes küldeni. A W megfigyelő jelet küld ezzel az eszközzel a világvonalán lévő A eseményből egy távoli B eseményhez, amely valamivel A fénykúpja alatt fekszik. Az 5.31a. ábrán ezt W nézőpontjából rajzoltuk le, de az 5.31b. ábrán az egészet újrarajzoltuk egy második, U megfigyelő nézőpontjából, aki gyorsan távolodik W-től (mondjuk egy A és B közötti ponttól), és akinek számára a B esemény korábbinak látszik, mint az A! (Ez az „átrajzolás” egy Poincaré-mozgás, amint azt korábban már leírtuk.) U egyidejű terei W nézőpontjából „megbillenteknek” látszanak, ezért láthatja U korábbinak a B eseményt, mint az A-t. Így a W által kibocsátott jelet U az időben visszafelé mozgónak látná!
Ez még nem teljesen ellentmondás. Ám nézzük most a dolgokat U nézőpontjából, szimmetrikusan (a speciális relativitás elve szerint). Egy harmadik, V megfigyelő U-tól W-vel ellentétes irányban távolodva, ugyanolyan eszközzel felszerelve, mint W, szintén ki tudna bocsátani egy a fénynél valamivel gyorsabb jelet az ő (azaz V) nézőpontjából hátrafelé, U irányába. U ezt a jelet is az időben hátrafelé mozgónak látná, most az ellentétes térbeli irányban. V leadhatna ezt a második jelet W felé hátra abban a pillanatban (B), amikor ő megkapja a W által küldött eredeti jelet. A második jel W-t egy C eseménynél éri el, amely U megítélése szerint korábbi, mint az eredeti kibocsátás A eseménye (5.32. ábra). Ám ennél még rosszabb, hogy a C esemény W saját világvonalán korábbi, mint az A, így W a C esemény bekövetkeztét valójában előbb tapasztalja, mint ahogy A-nál a jelet ő kibocsátja! Az üzenet, amelyet a V megfigyelő visszaküld W-hez, előzetes megegyezés alapján egyszerűen megismételhetné a B-ben kapott üzenetet. Így W világvonalán korábbi időpontban kapja meg ugyanazt az üzenetet, mint amelyet ő küld később! A két megfigyelőt elegendően nagy távolságra szétválasztva elérhető, hogy a visszatérő jel olyan nagy időkülönbséggel előzze meg az eredeti jelet, amilyennel csak akarjuk. W eredeti üzenete talán az, hogy eltörte a lábát. A visszaküldött üzenetet még azelőtt megkaphatná, mielőtt a baleset bekövetkezne, és így (feltehetően) szabad akaratából elkerülhetné azt!
Így a „fénynél gyorsabb” jeladás és Einstein relativitási elve együtt ordító ellentmondáshoz vezet normális „szabad akarat” érzésünkkel. A dolog ennél valójában még komolyabb. Elképzelhetnénk, hogy talán a „W megfigyelő” csupán egy úgy programozott mechanikus eszköz, hogy „IGEN” üzenetet küldjön, ha „NEM”-et kap és fordítva. V is lehet mechanikus eszköz, de úgy programozva, hogy ha „NEM”-et kap, küldje vissza a „NEM”-et, ha „IGEN”-t kap, küldje vissza az „IGEN”-t. Ez ugyanahhoz a lényeges ellentmondáshoz vezet, amelyet az előbb láttunk,102 most látszólag függetlenül attól a kérdéstől, van-e vagy nincs a W megfigyelőnek „szabad akarata”, és azt mondja nekünk, hogy egy fénynél gyorsabb jelet kibocsátó eszköz „nem működhet” mint fizikai lehetőség. Ennek a későbbiekben még lesznek rejtélyes következményei (6. fejezet).
Fogadjuk tehát el, hogy semmiféle jel – nem csupán a közönséges fizikai részecskék által hordozottak – nem kerülhet a fénykúpokon kívülre. Az előző érvelés a speciális relativitást használja, de a speciális elmélet szabályai lokálisan érvényesek maradnak az általános relativitáselméletben. A speciális relativitás lokális érvényessége mondja azt, hogy a fénykúpok magukba zárnak minden jelet, ezért ez igaz kell legyen az általános elméletben is. Látni fogjuk, hogyan befolyásolja ez a determinizmus kérdését ezekben az elméletekben. Emlékezzünk vissza, hogy a newtoni (vagy hamiltoni stb.) rendszerben a „determinizmus” azt jelenti, hogy „egy speciális időpontbeli kezdeti adatok” teljesen meghatározzák a viselkedést minden más időpontban. Ha a newtoni elméletben téridő-leírásmódot alkalmazunk, a „speciális időpont”, amelyben az adatokat előírjuk, a négydimenziós téridő valamely háromdimenziós „metszete” volna (azaz az egész tér abban az egy időpontban). A relativitáselméletben nincs globális „idő”, ami erre a célra kiválasztható volna. A szokásos eljárás az, hogy rugalmasabb hozzáállást fogadunk el. Bárki „ideje” megteszi. A speciális relativitáselméletben a kezdeti adatok előírására az előbbi „metszetnek” bármelyik megfigyelő egyidejű terét vehetjük. Az általános relativitáselméletben azonban az „egyidejű tér” fogalom nem jól meghatározott. Helyette a térszerű felület általánosabb fogalmát használhatjuk.103
A speciális relativitáselméletben a determinizmus úgy fogalmazható meg, hogy a tetszőlegesen adott S egyidejű téren rögzített kezdeti adatok meghatározzák a viselkedést az egész téridőben. (Ez a Maxwell-elméletre is igaz, amely valójában „speciális-relativisztikus” elmélet.) Lehet azonban erősebb állítást is tenni. Ha tudni akarjuk, mi fog történni az S jövőjében fekvő valamely P eseménynél, ahhoz a kezdeti adatokat nem kell az egész S-ben tudnunk, csak egy korlátos (véges) tartományában. Ennek oka az, hogy az „információ” nem terjedhet gyorsabban, mint a fény, így S-nek azok a pontjai, amelyek túl messze fekszenek ahhoz, hogy belőlük fényjel érje el P-t, nem lehetnek hatással P-re (lásd az 5.34. ábrát).104 Ez sokkal kielégítőbb, mint a newtoni esetben létrejövő helyzet, ahol elvileg tudnunk kellene, mi történt a teljes végtelen „metszeten”, hogy egyáltalán jóslatot tehessünk, mi fog történni tetszőleges pontban egy pillanattal később. Nincs megszorítás arra, milyen sebességgel terjedhet a newtoni információ, a newtoni erők valójában pillanatszerűek.
A „determinizmus” az általános relativitáselméletben jóval bonyolultabb dolog, mint a speciálisban, és csak néhány megjegyzést fogok ezzel kapcsolatban tenni. Elsősorban egy S térszerű felületet (és nem egyidejű felületet) kell használnunk a kezdeti adatok előírására. Ekkor az a helyzet, hogy az Einstein-egyenletek a gravitációs mező lokálisan determinisztikus viselkedését adják, feltéve (mint szokásosan), hogy az ENERGIA tenzorhoz járulékot adó anyagmezők determinisztikusan viselkednek. Vannak azonban jelentős bonyodalmak. Maga a téridő geometriája – fénykúp „kauzalitás”-szerkezetével együtt – most része annak, ami ténylegesen meghatározásra kerül. E fénykúpszerkezetet időben előre nem ismerjük, így nem tudjuk megmondani, S mely részeire van szükség, hogy meghatározzuk a viselkedést egy jövőbeli P eseménynél. Bizonyos szélsőséges esetekben előfordulhat, hogy az egész S sem elegendő, következésképpen a globális determinizmus elvész! (Nehéz kérdések kerülnek itt elő, és az általános relativitáselmélet egy fontos megoldatlan problémájához, az ún. „kozmikus cenzúrához” kapcsolódnak – aminek köze van a fekete lyukak létrejöttéhez (Tipler és mások 1980; vö. 7. fejezet) Nagyon valószínűtlennek látszik, hogy a „szélsőséges” gravitációs mezőknél esetleg bekövetkező, bármiféle „determinizmuskudarcnak” közvetlen hatása volna az emberi skálájú dolgokra,...de azért ez a hiány, nem teljesség, nem teljes érvényesség nyugtalanítja Penroset.
Kiszámíthatóság a klasszikus fizikában: hogyan is állunk?
E fejezetben végig próbáltam szemmel tartani a kiszámíthatóság kérdését, mint ami különbözik a determinizmusétól, és próbáltam jelezni, hogy amikor a „szabad akarat” és a szellemi jelenségek kérdéseit tárgyaljuk, akkor a kiszámíthatósági problémák legalább annyira fontosak, mint a determinizmus. Kiderült azonban, hogy a determinizmus önmagában sem egészen olyan világos a klasszikus elméletben, mint ahogy azt elhitették velünk. Láttuk, hogy a töltött részecske mozgásának klasszikus Lorentz-egyenlete zavaró problémákat vet fel. (Emlékezzünk Dirac „elfutó megoldásaira”.) Észrevettük azt is, hogy a determinizmussal az általános relativitáselméletben is vannak nehézségek. Amikor az ilyen elméletekben nincs determinizmus, akkor bizonyára nincs kiszámíthatóság sem. Mégis, egyik felidézett esetben sem látszik úgy, hogy a determinizmus hiányának számottevő közvetlen filozófiai jelentősége volna számunkra. Szabad akaratunk számára még nincs „hely” ezekben a jelenségekben: az első esetben azért, mert úgy gondoljuk, hogy pontszerű részecskére a klasszikus Lorentz-egyenlet (ahogy Dirac megoldotta) fizikailag nem megfelelő azon a szinten, ahol ezek a problémák fellépnek; a másodikban azért, mert azok a skálák, ahol a klasszikus általános relativitáselmélet ilyen problémákhoz vezethet (fekete lyukak stb.), teljesen eltérőek agyunk skáláitól.
Hogy állunk akkor most a kiszámíthatósággal a klasszikus elméletben? Ésszerű az a sejtés, hogy az általános relativitáselmélet helyzete nem különbözik jelentősen a speciálisétól – túl a kauzalitásban és a determinizmusban lévő különbségeken, amelyekről éppen az előbb beszéltem. Ahol a fizikai rendszer jövőbeli viselkedését a kezdeti adatok meghatározzák, ott ez a jövőbeli viselkedés (hasonló okokból, mint amelyeket a newtoni elméletnél kifejtettem) az adatok által kiszámíthatóan meghatározottnak látszik105 (eltekintve a nemkiszámíthatóságnak attól a „nem éppen segítőkész” típusától, amelyet Pour-El és Richards a hullámegyenletnél találtak – és amely folytonosan változó adatok mellett nem lép fel). Valójában nehéz látni, hogy bármelyik eddig megvizsgált fizikai elméletben lehetnének jelentős „nem kiszámítható” elemek. Azt biztosan várnunk kell, hogy az elméletek közül sokban bekövetkezhet az a „kaotikus” viselkedés, amikor nagyon kis változások a kezdeti adatokban hatalmas különbségeket okozhatnak az eredő viselkedésben. (Ez a helyzet látszik az általános relativitásban, vö. Misner 1969, Belinskii és mások 1970.) De amint az előbb említettem, nehéz azt látni, hogy a nemkiszámíthatóságnak ez a fajtája – azaz a „jósolhatatlanság” – bármilyen „hasznára” lehet egy eszköznek, amely megpróbálja „kiaknázni” a fizikai törvényekben lévő lehetséges nem kiszámítható elemeket. Ha az „értelem” bármiképp hasznosíthatja ezeket, akkor úgy látszik, a klasszikus fizikán kívül kell lenniük ezeknek az elemeknek. E kérdést később újra meg kell vizsgálnunk, miután már vetettünk egy pillantást a kvantumelméletre.
.........
1./
Szabad akaratunk számára még nincs „hely” ezekben a jelenségekben: az első esetben azért, mert úgy gondoljuk, hogy pontszerű részecskére a klasszikus Lorentz-egyenlet (ahogy Dirac megoldotta) fizikailag nem megfelelő azon a szinten, ahol ezek a problémák fellépnek; a másodikban azért, mert azok a skálák, ahol a klasszikus általános relativitáselmélet ilyen problémákhoz vezethet (fekete lyukak stb.), teljesen eltérőek agyunk skáláitól. - írja.
…teljesen eltérőek agyunk skáláitól…és előtte zárójelben, hogy például hol uralkodnak azok az eltérő skálák (fekete lyukak stb.)
Többször felvillantja azt, amit a magamfajta halandó szeretne elkapni, hiú remény, hogy megérteni, csak elkapni, vagy legalábbis megérinteni.
Egy régen olvasott- elég jó – fantasztikus regényben egy űrhajót magába ránt egy fekete lyuk. Öten vagy hatan utaztak a hajón. A könyv utolsó oldalának történései már a „szingularitáson” túlról szólnak: az események helyszíne ott a lyuk túloldalán nem a túlvilág, és nem is az a klinikai halálból visszatértek emlékidézéseiben derengő gyöngyház-szín szórású, sejtelmes, békés, hívogató fény (nagyon szeretem Kandinszkij: A fény, amely nem okoz fájdalmat című festményét); nem, ez a valami ahová az került ami valaha a hajó és utasai voltak, ez egy az elemei közötti kapcsolatot, párbeszédet, egymás érzékelését lehetővé tevő környezet…és az űrhajósok, vagyis azok a még szubatomi részecskékhez sem hasonlítható valamik, amik belőlük maradtak, csodálva érzékelik a helyet, a helyzetet, ezt a gyöngyházfény –világot, és rögtön közlik is „egymással”, amit „átélnek”, „éreznek”, „érzékelnek”, „észlelnek” és „látnak”.
2./
De amint az előbb említettem, nehéz azt látni, hogy a nemkiszámíthatóságnak ez a fajtája – azaz a „jósolhatatlanság” – bármilyen „hasznára” lehet egy eszköznek, amely megpróbálja „kiaknázni” a fizikai törvényekben lévő lehetséges nem kiszámítható elemeket. Ha az „értelem” bármiképp hasznosíthatja ezeket, akkor úgy látszik, a klasszikus fizikán kívül kell lenniük ezeknek az elemeknek. E kérdést később újra meg kell vizsgálnunk, miután már vetettünk egy pillantást a kvantumelméletre.
…
… Ha az „értelem” bármiképp hasznosíthatja ezeket, akkor úgy látszik, a klasszikus fizikán kívül kell lenniük ezeknek az elemeknek…
…
„értelem”
…
’a valami bennünk ül és figyel’ – kapisgáltam ezt valamikor negyedikes gimnazista koromban egy írásomban.
„Én túllépek e mai kocsmán,
az értelemig és tovább!” [József Attila]
Tömeg, anyag és valóság
Tekintsük röviden át a világnak azt a képét, amelyet a klasszikus fizika nyújt számunkra. Először is van egy téridő, amely elsődleges szerepet játszik mint az összes különböző fizikai tevékenység arénája. Másodszor vannak fizikai objektumok, amelyek átengedik magukat ennek a tevékenységnek, de pontos matematikai törvényekkel korlátozottan.
A könyv matematikai fejezeteiben azt fejtegeti, hogy a matematikát viszont nem korlátozza a valóság (úgy rémlik ott, ahol Gödelről, a nemteljességről, az ellentmondásmentességről ír. Ha jól értem a fizikai világban az a valóban létező, az az igaz, ahol a jelenséget leíró fizika elméletben semmiféle ellentmondás nem található
A fizikai objektumok kétfélék: részecskék és mezők. A részecskék valódi természetéről és megkülönböztető jegyeiről kevés szó esik, tudjuk azt, hogy mindegyiknek van saját világvonala és egyedi (nyugalmi) tömege, esetleg elektromos töltése stb. A mezők viszont nagyon specifikusak – az elektromágneses mező a Maxwell-egyenletek tárgya, a gravitációs mező az Einstein-egyenleteké.
Van bizonyos kétértelműség abban, hogyan kell a részecskéket kezelni. Azokat, amelyek tömege olyan kicsi, hogy befolyásuk a mezőkre elhanyagolható, próbarészecskéknek nevezzük – és ezek mozgása a tereknek adott válaszként egyértelmű. A Lorentz-erő leírja a próbarészecske válaszát az elektromágneses mezőre, a geodetikus törvény a választ a gravitációs mezőre (megfelelő kombinációban, ha mindkét mező jelen van). Ehhez a részecskéket pontszerűeknek, azaz egydimenziós világvonalúaknak kell tekintenünk. Ha azonban figyelembe kell vennünk a részecskék hatásait a mezőkre (és így a többi részecskére) – azaz ha a részecskék forrásai a mezőknek –, akkor térben valamennyire kiterjedt objektumoknak kell azokat tekintenünk. Máskülönben a mezők minden részecske közvetlen közelében végtelenné válnak. Ezek a kiterjedt források szolgáltatják a (ρ, j) töltés–áram-eloszlást, amely a Maxwell-egyenletekhez, és az ENERGIA tenzort, amely az Einstein-egyenletekhez szükséges. Mindezekhez járul még, hogy a téridő – amelyben mind e részecskék és mezők tartózkodnak – változó szerkezetű, ami önmagában közvetlenül leírja a gravitációt. Az „aréna” csatlakozik a benne végbemenő történéshez!
Ezt tanította nekünk a klasszikus fizika a fizikai valóság természetéről. Világos, hogy jó sokat tanultunk, és az is, hogy nem kell túlságosan önelégülteknek lennünk; a képet, amelyet valamikor kialakítottunk, későbbi és mélyebb meglátások mindig felboríthatják. A következő fejezetben látni fogjuk, hogy még a relativitáselmélet által hozott forradalmi változások is szinte a jelentéktelenségbe szürkülnek a kvantumelmélet által hozottak mellett.
Mi az „anyag”? Az a valódi szubsztancia, amelyből a valóságos fizikai objektumok – a világ „dolgai” – összetevődnek….
Milyen mennyiséggel mérjük ezt a szubsztanciát? Elemi fizikai tankönyveinkben ott van Newton világos válasza. Egy objektum vagy objektumrendszer tömege méri a tartalmazott anyag mennyiségét. Ez valóban helyesnek látszik – nincs más fizikai mennyiség, amely komolyan versenyezhet a tömeggel, mint a teljes szubsztancia igazi mértéke. Mi több, ez megmarad: bármilyen rendszer tömege, és így teljes anyagi tartalma, mindig ugyanaz kell maradjon.
Einstein nevezetes képlete a speciális relativitáselméletből, az
E = mc2
mégis azt mondja nekünk, hogy a tömeg (m) és energia (E) átváltoztathatók egymásba. Például amikor egy uránatom elbomlik, kisebb részekre hasad szét, akkor e részek összes tömege, ha meg tudnánk mérni, kisebb lenne, mint az uránatom eredeti tömege; ám ha figyelembe vesszük minden egyes darab mozgásának energiáját – a kinetikus energiát,106 – és c2-tel osztva tömegértékké alakítjuk át (mert E = mc2), akkor azt találjuk, hogy a teljes végösszeg változatlan. A tömeg valóban megmarad, de mert részben energiából áll, most már kevésbé világos, hogy a valóságos szubsztancia mértéke. Az energia végül is függ a sebességtől, amellyel a szubsztancia mozog. Egy expresszvonat mozgási energiája jelentős, de ha úgy adódik, hogy éppen ezen a vonaton ülünk, akkor saját nézőpontunkból a vonat egyáltalán nem mozog. A mozgás energiáját (bár az egyes részecskék véletlenszerű mozgásából származó hőenergiát nem) a nézőpont alkalmas megválasztásával „nullára csökkentettük”. Egy meglepő példaként, ahol az Einstein-féle tömeg–energia összefüggés hatása a legszélsőségesebb, tekintsük a szubatomi részecskék egyik típusának, a π0-mezonnak a bomlását. Ez biztosan anyagi részecske, jól meghatározott (pozitív) tömege van. Úgy 10–16 másodperc után szétbomlik (mint előbb az uránatom, csak annál sokkal gyorsabban) – majdnem mindig két fotonra (5.35. ábra). A π0-mezonhoz képest nyugvó megfigyelő szerint mindkét foton az energia felét, és valójában a π0-mezon tömegének felét viszi el. Ez a „fotontömeg” olyan bizonytalan fajta: tiszta energia. Ha gyorsan utaznánk az egyik foton irányában, akkor tömeg-energiáját olyan kis értékre csökkenthetnénk, amilyenre csak akarjuk – lévén egy foton belső tömege (vagy nyugalmi tömege, mint azt rövidesen tárgyaljuk) nulla. Mindez hozzájárul a megmaradó tömeg konzisztens képéhez, amely azonban nem egészen az, mint korábban volt. A tömeg egyfajta értelemben még mindig mérheti az „anyag mennyiségét”, de a nézőpont világosan megváltozott: mivel a tömeg egyenértékű az energiával, egy rendszer tömege, az energiához hasonlóan, függ a megfigyelő mozgásától!
A megmaradó mennyiség, amely átveszi a tömeg szerepét, egy energia-impulzus négyesvektornak nevezett valami. A Minkowski-tér O kezdőpontjában nyíllal (vektorral) ábrázolható, O jövőbe mutató fénykúpjának belsejébe (vagy a foton szélsőséges esetében a kúpra) mutat; lásd 5.36. ábra. Ez a nyíl, amely ugyanabba az irányba mutat, mint az objektum világvonala, minden információt tartalmaz energiájáról, tömegéről és impulzusáról. Így a nyíl hegyének „t értéke” (vagy „magassága”) valamely megfigyelő rendszerében mérve megadja az objektum tömegét (vagy c2-tel osztott energiáját) a megfigyelő szerint, míg a térbeli összetevő az impulzust (c-vel osztva).
E nyíl „Minkowski-hossza” a nyugalmi tömeg néven ismert, fontos mennyiség, amely a tömeget adja meg az objektumhoz képest nyugvó megfigyelő számára. Próbálkozhatnánk azzal, hogy ezt válasszuk az „anyagmennyiség” jó mértékének. Azonban nem additív: ha egy rendszer kétfelé hasad, akkor az eredeti nyugalmi tömeg nem a két új nyugalmi tömeg összege. Emlékezzünk a π0-mezon előbb vizsgált bomlására. A π0-mezon nyugalmi tömege pozitív, míg a keletkező fotonoké nulla. Az egész nyílra (négyesvektorra) azonban érvényes az additivitási tulajdonság, de most az 5.6. ábrán bemutatott vektorösszegzési szabály értelmében kell „összeadnunk”. Most ez a teljes nyíl az „anyag mennyiségére” vonatkozó mértékünk!
Gondoljunk most Maxwell elektromágneses mezőjére. Megfigyeltük, hogy energiát hordoz. Az E = mc2 szerint tömegének is kell lennie. Így Maxwell mezője szintén anyag! Ezt most biztosan el kell fogadnunk, mert a Maxwell-mezőnek szoros köze van az erőkhöz, amelyek a részecskéket összetartják. Bármely test tömegéhez lényeges járulékot107 kell adjanak a belsejében lévő elektromágneses mezők.
Mi a helyzet Einstein gravitációs mezőjével? Sok tekintetben Maxwell mezőjére emlékeztet. Hasonlóan ahhoz, ahogy Maxwell elméletében a mozgó, töltött részecskék elektromágneses hullámokat tudnak kibocsátani, a mozgó, tömeggel rendelkező testek (Einstein elmélete szerint) gravitációs hullámokat bocsátanak ki – amelyek, az elektromágneses hullámokhoz hasonlóan, a fény sebességével terjednek és energiát hordoznak. Ezt az energiát mégsem a szokásos módon, az ENERGIA tenzorral mérjük, amelyre korábban utaltam. (Tiszta) gravitációs hullámban ez a tenzor mindenhol nulla! Mindazonáltal helyezkedhetünk arra a nézőpontra, hogy valahogy a téridő görbülete (amit most teljesen a WEYL tenzor ad meg) mutathatja a gravitációs hullámok „szövedékét”. A gravitációs energia azonban nemlokális, ami azt jelenti, hogy a téridő görbületének csupán korlátos tartományban való vizsgálatával nem lehet meghatározni az energia mértékét. A gravitációs mező energiája – és ezért tömege – sikamlós angolna, nem hagyja magát egy adott helyen elcsípni. Mindazonáltal komolyan kell venni. Biztosan ott van, és számításba kell venni, hogy a tömeg általánosan megmaradhasson. Van a tömegnek egy jó (és pozitív) mértéke (Bondi 1960, Sachs 1962), amely alkalmazható a gravitációs hullámokra, de a nemlokalitás olyan, hogy ez a mérték olykor nemzérus lehet a téridő sík tartományaiban – a sugárzás két hulláma között (hasonlóan, mint a hurrikán magján belüli csend) –, ahol a téridő teljesen görbületmentes (vö. Penrose és Rindler 1986, 427. o.), azaz WEYL és RICCI egyaránt zérus! Ilyen esetekben, úgy látszik, arra kell következtetnünk, hogy ha ez a tömeg-energia egyáltalán megfogható, akkor ebben a sík üres térben kell legyen – minden anyagtól vagy mezőtől tökéletesen mentes tartományban. Ilyen furcsa körülmények között „anyagmennyiségünk” most vagy ott van az üres tartományok legüresebbjében, vagy egyáltalán nincs sehol!
Ez igazi paradoxonnak látszik. Mégis határozott velejárója annak, amit legjobb klasszikus elméleteink – és ezek valóban szuperelméletek – világunk „valóságos” anyagának természetéről mondanak. Az anyagi valóság a klasszikus elmélet szerint, nem is beszélve a kvantumelméletről, amelyet éppen kifejteni készülünk, sokkal ködösebb dolog, mint azt gondoltuk. Mennyiségi meghatározása – sőt hogy vajon ott van-e vagy sem – határozottan kényes kérdésektől függ, és nem lehet csupán lokálisan megállapítani! Ha ez a nemlokalitás rejtélyesnek látszik, akkor készüljünk fel még sokkal nagyobb megrázkódtatásokra.
...Szirénének...
Ez a torzító hatás úgy ismert, mint a gravitáció árapályjelensége. Ha a Föld középpontját a Holddal, a részecskegömböt pedig a Föld felületével helyettesítjük, akkor pontosan előttünk áll a Hold árapályt előidéző hatása, mind a Hold irányában, mind az ellentétes irányban kidagadás jön létre. Az árapályjelenség a gravitációs mezőknek általános tulajdonsága, amelyet szabadeséssel nem lehet „kioltani”. Ez a jelenség a newtoni gravitációs mező nemegyenletességét méri. (Az árapálytorzítás nagysága a vonzócentrumtól mért távolság inverz köbe és nem inverz négyzete szerint csökken.)
Emlékezzünk arra, hogy a relativitáselméletben az anyagi testek nem mozoghatnak a fénynél gyorsabban – abban az értelemben, hogy világvonalaiknak mindig a fénykúpokon belül kell haladniuk (vö. 5.29. ábra). (Az általános relativitáselméletben a dolgokat ilyen lokális módon kell megfogalmaznunk. A fénykúpok nem rendeződnek el egyenletesen, így nem volna sok értelme azt mondani, hogy egy nagyon távoli részecske sebessége felülmúlja-e az itteni fénysebességet.) A fotonok világvonalai a fénykúpok mentén fekszenek, de semmilyen részecske világvonala nem haladhat a kúpokon kívül. Valójában egy általánosabb állításnak kell igaznak lennie, nevezetesen annak, hogy semmilyen jel nem mehet a fénykúpon kívül.
Hogy megértsük, miért kell ennek így lennie, nézzük meg a Minkowski-térről rajzolt képeket (5.31. ábra). Tegyük fel, hogy készítettünk egy eszközt, amely a fényénél kicsit nagyobb sebességű jelet képes küldeni. A W megfigyelő jelet küld ezzel az eszközzel a világvonalán lévő A eseményből egy távoli B eseményhez, amely valamivel A fénykúpja alatt fekszik. Az 5.31a. ábrán ezt W nézőpontjából rajzoltuk le, de az 5.31b. ábrán az egészet újrarajzoltuk egy második, U megfigyelő nézőpontjából, aki gyorsan távolodik W-től (mondjuk egy A és B közötti ponttól), és akinek számára a B esemény korábbinak látszik, mint az A! (Ez az „átrajzolás” egy Poincaré-mozgás, amint azt korábban már leírtuk.) U egyidejű terei W nézőpontjából „megbillenteknek” látszanak, ezért láthatja U korábbinak a B eseményt, mint az A-t. Így a W által kibocsátott jelet U az időben visszafelé mozgónak látná!
Ez még nem teljesen ellentmondás. Ám nézzük most a dolgokat U nézőpontjából, szimmetrikusan (a speciális relativitás elve szerint). Egy harmadik, V megfigyelő U-tól W-vel ellentétes irányban távolodva, ugyanolyan eszközzel felszerelve, mint W, szintén ki tudna bocsátani egy a fénynél valamivel gyorsabb jelet az ő (azaz V) nézőpontjából hátrafelé, U irányába. U ezt a jelet is az időben hátrafelé mozgónak látná, most az ellentétes térbeli irányban. V leadhatna ezt a második jelet W felé hátra abban a pillanatban (B), amikor ő megkapja a W által küldött eredeti jelet. A második jel W-t egy C eseménynél éri el, amely U megítélése szerint korábbi, mint az eredeti kibocsátás A eseménye (5.32. ábra). Ám ennél még rosszabb, hogy a C esemény W saját világvonalán korábbi, mint az A, így W a C esemény bekövetkeztét valójában előbb tapasztalja, mint ahogy A-nál a jelet ő kibocsátja! Az üzenet, amelyet a V megfigyelő visszaküld W-hez, előzetes megegyezés alapján egyszerűen megismételhetné a B-ben kapott üzenetet. Így W világvonalán korábbi időpontban kapja meg ugyanazt az üzenetet, mint amelyet ő küld később! A két megfigyelőt elegendően nagy távolságra szétválasztva elérhető, hogy a visszatérő jel olyan nagy időkülönbséggel előzze meg az eredeti jelet, amilyennel csak akarjuk. W eredeti üzenete talán az, hogy eltörte a lábát. A visszaküldött üzenetet még azelőtt megkaphatná, mielőtt a baleset bekövetkezne, és így (feltehetően) szabad akaratából elkerülhetné azt!
Így a „fénynél gyorsabb” jeladás és Einstein relativitási elve együtt ordító ellentmondáshoz vezet normális „szabad akarat” érzésünkkel. A dolog ennél valójában még komolyabb. Elképzelhetnénk, hogy talán a „W megfigyelő” csupán egy úgy programozott mechanikus eszköz, hogy „IGEN” üzenetet küldjön, ha „NEM”-et kap és fordítva. V is lehet mechanikus eszköz, de úgy programozva, hogy ha „NEM”-et kap, küldje vissza a „NEM”-et, ha „IGEN”-t kap, küldje vissza az „IGEN”-t. Ez ugyanahhoz a lényeges ellentmondáshoz vezet, amelyet az előbb láttunk,102 most látszólag függetlenül attól a kérdéstől, van-e vagy nincs a W megfigyelőnek „szabad akarata”, és azt mondja nekünk, hogy egy fénynél gyorsabb jelet kibocsátó eszköz „nem működhet” mint fizikai lehetőség. Ennek a későbbiekben még lesznek rejtélyes következményei (6. fejezet).
Fogadjuk tehát el, hogy semmiféle jel – nem csupán a közönséges fizikai részecskék által hordozottak – nem kerülhet a fénykúpokon kívülre. Az előző érvelés a speciális relativitást használja, de a speciális elmélet szabályai lokálisan érvényesek maradnak az általános relativitáselméletben. A speciális relativitás lokális érvényessége mondja azt, hogy a fénykúpok magukba zárnak minden jelet, ezért ez igaz kell legyen az általános elméletben is. Látni fogjuk, hogyan befolyásolja ez a determinizmus kérdését ezekben az elméletekben. Emlékezzünk vissza, hogy a newtoni (vagy hamiltoni stb.) rendszerben a „determinizmus” azt jelenti, hogy „egy speciális időpontbeli kezdeti adatok” teljesen meghatározzák a viselkedést minden más időpontban. Ha a newtoni elméletben téridő-leírásmódot alkalmazunk, a „speciális időpont”, amelyben az adatokat előírjuk, a négydimenziós téridő valamely háromdimenziós „metszete” volna (azaz az egész tér abban az egy időpontban). A relativitáselméletben nincs globális „idő”, ami erre a célra kiválasztható volna. A szokásos eljárás az, hogy rugalmasabb hozzáállást fogadunk el. Bárki „ideje” megteszi. A speciális relativitáselméletben a kezdeti adatok előírására az előbbi „metszetnek” bármelyik megfigyelő egyidejű terét vehetjük. Az általános relativitáselméletben azonban az „egyidejű tér” fogalom nem jól meghatározott. Helyette a térszerű felület általánosabb fogalmát használhatjuk.103
A speciális relativitáselméletben a determinizmus úgy fogalmazható meg, hogy a tetszőlegesen adott S egyidejű téren rögzített kezdeti adatok meghatározzák a viselkedést az egész téridőben. (Ez a Maxwell-elméletre is igaz, amely valójában „speciális-relativisztikus” elmélet.) Lehet azonban erősebb állítást is tenni. Ha tudni akarjuk, mi fog történni az S jövőjében fekvő valamely P eseménynél, ahhoz a kezdeti adatokat nem kell az egész S-ben tudnunk, csak egy korlátos (véges) tartományában. Ennek oka az, hogy az „információ” nem terjedhet gyorsabban, mint a fény, így S-nek azok a pontjai, amelyek túl messze fekszenek ahhoz, hogy belőlük fényjel érje el P-t, nem lehetnek hatással P-re (lásd az 5.34. ábrát).104 Ez sokkal kielégítőbb, mint a newtoni esetben létrejövő helyzet, ahol elvileg tudnunk kellene, mi történt a teljes végtelen „metszeten”, hogy egyáltalán jóslatot tehessünk, mi fog történni tetszőleges pontban egy pillanattal később. Nincs megszorítás arra, milyen sebességgel terjedhet a newtoni információ, a newtoni erők valójában pillanatszerűek.
A „determinizmus” az általános relativitáselméletben jóval bonyolultabb dolog, mint a speciálisban, és csak néhány megjegyzést fogok ezzel kapcsolatban tenni. Elsősorban egy S térszerű felületet (és nem egyidejű felületet) kell használnunk a kezdeti adatok előírására. Ekkor az a helyzet, hogy az Einstein-egyenletek a gravitációs mező lokálisan determinisztikus viselkedését adják, feltéve (mint szokásosan), hogy az ENERGIA tenzorhoz járulékot adó anyagmezők determinisztikusan viselkednek. Vannak azonban jelentős bonyodalmak. Maga a téridő geometriája – fénykúp „kauzalitás”-szerkezetével együtt – most része annak, ami ténylegesen meghatározásra kerül. E fénykúpszerkezetet időben előre nem ismerjük, így nem tudjuk megmondani, S mely részeire van szükség, hogy meghatározzuk a viselkedést egy jövőbeli P eseménynél. Bizonyos szélsőséges esetekben előfordulhat, hogy az egész S sem elegendő, következésképpen a globális determinizmus elvész! (Nehéz kérdések kerülnek itt elő, és az általános relativitáselmélet egy fontos megoldatlan problémájához, az ún. „kozmikus cenzúrához” kapcsolódnak – aminek köze van a fekete lyukak létrejöttéhez (Tipler és mások 1980; vö. 7. fejezet) Nagyon valószínűtlennek látszik, hogy a „szélsőséges” gravitációs mezőknél esetleg bekövetkező, bármiféle „determinizmuskudarcnak” közvetlen hatása volna az emberi skálájú dolgokra,...de azért ez a hiány, nem teljesség, nem teljes érvényesség nyugtalanítja Penroset.
Kiszámíthatóság a klasszikus fizikában: hogyan is állunk?
E fejezetben végig próbáltam szemmel tartani a kiszámíthatóság kérdését, mint ami különbözik a determinizmusétól, és próbáltam jelezni, hogy amikor a „szabad akarat” és a szellemi jelenségek kérdéseit tárgyaljuk, akkor a kiszámíthatósági problémák legalább annyira fontosak, mint a determinizmus. Kiderült azonban, hogy a determinizmus önmagában sem egészen olyan világos a klasszikus elméletben, mint ahogy azt elhitették velünk. Láttuk, hogy a töltött részecske mozgásának klasszikus Lorentz-egyenlete zavaró problémákat vet fel. (Emlékezzünk Dirac „elfutó megoldásaira”.) Észrevettük azt is, hogy a determinizmussal az általános relativitáselméletben is vannak nehézségek. Amikor az ilyen elméletekben nincs determinizmus, akkor bizonyára nincs kiszámíthatóság sem. Mégis, egyik felidézett esetben sem látszik úgy, hogy a determinizmus hiányának számottevő közvetlen filozófiai jelentősége volna számunkra. Szabad akaratunk számára még nincs „hely” ezekben a jelenségekben: az első esetben azért, mert úgy gondoljuk, hogy pontszerű részecskére a klasszikus Lorentz-egyenlet (ahogy Dirac megoldotta) fizikailag nem megfelelő azon a szinten, ahol ezek a problémák fellépnek; a másodikban azért, mert azok a skálák, ahol a klasszikus általános relativitáselmélet ilyen problémákhoz vezethet (fekete lyukak stb.), teljesen eltérőek agyunk skáláitól.
Hogy állunk akkor most a kiszámíthatósággal a klasszikus elméletben? Ésszerű az a sejtés, hogy az általános relativitáselmélet helyzete nem különbözik jelentősen a speciálisétól – túl a kauzalitásban és a determinizmusban lévő különbségeken, amelyekről éppen az előbb beszéltem. Ahol a fizikai rendszer jövőbeli viselkedését a kezdeti adatok meghatározzák, ott ez a jövőbeli viselkedés (hasonló okokból, mint amelyeket a newtoni elméletnél kifejtettem) az adatok által kiszámíthatóan meghatározottnak látszik105 (eltekintve a nemkiszámíthatóságnak attól a „nem éppen segítőkész” típusától, amelyet Pour-El és Richards a hullámegyenletnél találtak – és amely folytonosan változó adatok mellett nem lép fel). Valójában nehéz látni, hogy bármelyik eddig megvizsgált fizikai elméletben lehetnének jelentős „nem kiszámítható” elemek. Azt biztosan várnunk kell, hogy az elméletek közül sokban bekövetkezhet az a „kaotikus” viselkedés, amikor nagyon kis változások a kezdeti adatokban hatalmas különbségeket okozhatnak az eredő viselkedésben. (Ez a helyzet látszik az általános relativitásban, vö. Misner 1969, Belinskii és mások 1970.) De amint az előbb említettem, nehéz azt látni, hogy a nemkiszámíthatóságnak ez a fajtája – azaz a „jósolhatatlanság” – bármilyen „hasznára” lehet egy eszköznek, amely megpróbálja „kiaknázni” a fizikai törvényekben lévő lehetséges nem kiszámítható elemeket. Ha az „értelem” bármiképp hasznosíthatja ezeket, akkor úgy látszik, a klasszikus fizikán kívül kell lenniük ezeknek az elemeknek. E kérdést később újra meg kell vizsgálnunk, miután már vetettünk egy pillantást a kvantumelméletre.
.........
1./
Szabad akaratunk számára még nincs „hely” ezekben a jelenségekben: az első esetben azért, mert úgy gondoljuk, hogy pontszerű részecskére a klasszikus Lorentz-egyenlet (ahogy Dirac megoldotta) fizikailag nem megfelelő azon a szinten, ahol ezek a problémák fellépnek; a másodikban azért, mert azok a skálák, ahol a klasszikus általános relativitáselmélet ilyen problémákhoz vezethet (fekete lyukak stb.), teljesen eltérőek agyunk skáláitól. - írja.
…teljesen eltérőek agyunk skáláitól…és előtte zárójelben, hogy például hol uralkodnak azok az eltérő skálák (fekete lyukak stb.)
Többször felvillantja azt, amit a magamfajta halandó szeretne elkapni, hiú remény, hogy megérteni, csak elkapni, vagy legalábbis megérinteni.
Egy régen olvasott- elég jó – fantasztikus regényben egy űrhajót magába ránt egy fekete lyuk. Öten vagy hatan utaztak a hajón. A könyv utolsó oldalának történései már a „szingularitáson” túlról szólnak: az események helyszíne ott a lyuk túloldalán nem a túlvilág, és nem is az a klinikai halálból visszatértek emlékidézéseiben derengő gyöngyház-szín szórású, sejtelmes, békés, hívogató fény (nagyon szeretem Kandinszkij: A fény, amely nem okoz fájdalmat című festményét); nem, ez a valami ahová az került ami valaha a hajó és utasai voltak, ez egy az elemei közötti kapcsolatot, párbeszédet, egymás érzékelését lehetővé tevő környezet…és az űrhajósok, vagyis azok a még szubatomi részecskékhez sem hasonlítható valamik, amik belőlük maradtak, csodálva érzékelik a helyet, a helyzetet, ezt a gyöngyházfény –világot, és rögtön közlik is „egymással”, amit „átélnek”, „éreznek”, „érzékelnek”, „észlelnek” és „látnak”.
2./
De amint az előbb említettem, nehéz azt látni, hogy a nemkiszámíthatóságnak ez a fajtája – azaz a „jósolhatatlanság” – bármilyen „hasznára” lehet egy eszköznek, amely megpróbálja „kiaknázni” a fizikai törvényekben lévő lehetséges nem kiszámítható elemeket. Ha az „értelem” bármiképp hasznosíthatja ezeket, akkor úgy látszik, a klasszikus fizikán kívül kell lenniük ezeknek az elemeknek. E kérdést később újra meg kell vizsgálnunk, miután már vetettünk egy pillantást a kvantumelméletre.
…
… Ha az „értelem” bármiképp hasznosíthatja ezeket, akkor úgy látszik, a klasszikus fizikán kívül kell lenniük ezeknek az elemeknek…
…
„értelem”
…
’a valami bennünk ül és figyel’ – kapisgáltam ezt valamikor negyedikes gimnazista koromban egy írásomban.
„Én túllépek e mai kocsmán,
az értelemig és tovább!” [József Attila]
Tömeg, anyag és valóság
Tekintsük röviden át a világnak azt a képét, amelyet a klasszikus fizika nyújt számunkra. Először is van egy téridő, amely elsődleges szerepet játszik mint az összes különböző fizikai tevékenység arénája. Másodszor vannak fizikai objektumok, amelyek átengedik magukat ennek a tevékenységnek, de pontos matematikai törvényekkel korlátozottan.
A könyv matematikai fejezeteiben azt fejtegeti, hogy a matematikát viszont nem korlátozza a valóság (úgy rémlik ott, ahol Gödelről, a nemteljességről, az ellentmondásmentességről ír. Ha jól értem a fizikai világban az a valóban létező, az az igaz, ahol a jelenséget leíró fizika elméletben semmiféle ellentmondás nem található
A fizikai objektumok kétfélék: részecskék és mezők. A részecskék valódi természetéről és megkülönböztető jegyeiről kevés szó esik, tudjuk azt, hogy mindegyiknek van saját világvonala és egyedi (nyugalmi) tömege, esetleg elektromos töltése stb. A mezők viszont nagyon specifikusak – az elektromágneses mező a Maxwell-egyenletek tárgya, a gravitációs mező az Einstein-egyenleteké.
Van bizonyos kétértelműség abban, hogyan kell a részecskéket kezelni. Azokat, amelyek tömege olyan kicsi, hogy befolyásuk a mezőkre elhanyagolható, próbarészecskéknek nevezzük – és ezek mozgása a tereknek adott válaszként egyértelmű. A Lorentz-erő leírja a próbarészecske válaszát az elektromágneses mezőre, a geodetikus törvény a választ a gravitációs mezőre (megfelelő kombinációban, ha mindkét mező jelen van). Ehhez a részecskéket pontszerűeknek, azaz egydimenziós világvonalúaknak kell tekintenünk. Ha azonban figyelembe kell vennünk a részecskék hatásait a mezőkre (és így a többi részecskére) – azaz ha a részecskék forrásai a mezőknek –, akkor térben valamennyire kiterjedt objektumoknak kell azokat tekintenünk. Máskülönben a mezők minden részecske közvetlen közelében végtelenné válnak. Ezek a kiterjedt források szolgáltatják a (ρ, j) töltés–áram-eloszlást, amely a Maxwell-egyenletekhez, és az ENERGIA tenzort, amely az Einstein-egyenletekhez szükséges. Mindezekhez járul még, hogy a téridő – amelyben mind e részecskék és mezők tartózkodnak – változó szerkezetű, ami önmagában közvetlenül leírja a gravitációt. Az „aréna” csatlakozik a benne végbemenő történéshez!
Ezt tanította nekünk a klasszikus fizika a fizikai valóság természetéről. Világos, hogy jó sokat tanultunk, és az is, hogy nem kell túlságosan önelégülteknek lennünk; a képet, amelyet valamikor kialakítottunk, későbbi és mélyebb meglátások mindig felboríthatják. A következő fejezetben látni fogjuk, hogy még a relativitáselmélet által hozott forradalmi változások is szinte a jelentéktelenségbe szürkülnek a kvantumelmélet által hozottak mellett.
Mi az „anyag”? Az a valódi szubsztancia, amelyből a valóságos fizikai objektumok – a világ „dolgai” – összetevődnek….
Milyen mennyiséggel mérjük ezt a szubsztanciát? Elemi fizikai tankönyveinkben ott van Newton világos válasza. Egy objektum vagy objektumrendszer tömege méri a tartalmazott anyag mennyiségét. Ez valóban helyesnek látszik – nincs más fizikai mennyiség, amely komolyan versenyezhet a tömeggel, mint a teljes szubsztancia igazi mértéke. Mi több, ez megmarad: bármilyen rendszer tömege, és így teljes anyagi tartalma, mindig ugyanaz kell maradjon.
Einstein nevezetes képlete a speciális relativitáselméletből, az
E = mc2
mégis azt mondja nekünk, hogy a tömeg (m) és energia (E) átváltoztathatók egymásba. Például amikor egy uránatom elbomlik, kisebb részekre hasad szét, akkor e részek összes tömege, ha meg tudnánk mérni, kisebb lenne, mint az uránatom eredeti tömege; ám ha figyelembe vesszük minden egyes darab mozgásának energiáját – a kinetikus energiát,106 – és c2-tel osztva tömegértékké alakítjuk át (mert E = mc2), akkor azt találjuk, hogy a teljes végösszeg változatlan. A tömeg valóban megmarad, de mert részben energiából áll, most már kevésbé világos, hogy a valóságos szubsztancia mértéke. Az energia végül is függ a sebességtől, amellyel a szubsztancia mozog. Egy expresszvonat mozgási energiája jelentős, de ha úgy adódik, hogy éppen ezen a vonaton ülünk, akkor saját nézőpontunkból a vonat egyáltalán nem mozog. A mozgás energiáját (bár az egyes részecskék véletlenszerű mozgásából származó hőenergiát nem) a nézőpont alkalmas megválasztásával „nullára csökkentettük”. Egy meglepő példaként, ahol az Einstein-féle tömeg–energia összefüggés hatása a legszélsőségesebb, tekintsük a szubatomi részecskék egyik típusának, a π0-mezonnak a bomlását. Ez biztosan anyagi részecske, jól meghatározott (pozitív) tömege van. Úgy 10–16 másodperc után szétbomlik (mint előbb az uránatom, csak annál sokkal gyorsabban) – majdnem mindig két fotonra (5.35. ábra). A π0-mezonhoz képest nyugvó megfigyelő szerint mindkét foton az energia felét, és valójában a π0-mezon tömegének felét viszi el. Ez a „fotontömeg” olyan bizonytalan fajta: tiszta energia. Ha gyorsan utaznánk az egyik foton irányában, akkor tömeg-energiáját olyan kis értékre csökkenthetnénk, amilyenre csak akarjuk – lévén egy foton belső tömege (vagy nyugalmi tömege, mint azt rövidesen tárgyaljuk) nulla. Mindez hozzájárul a megmaradó tömeg konzisztens képéhez, amely azonban nem egészen az, mint korábban volt. A tömeg egyfajta értelemben még mindig mérheti az „anyag mennyiségét”, de a nézőpont világosan megváltozott: mivel a tömeg egyenértékű az energiával, egy rendszer tömege, az energiához hasonlóan, függ a megfigyelő mozgásától!
A megmaradó mennyiség, amely átveszi a tömeg szerepét, egy energia-impulzus négyesvektornak nevezett valami. A Minkowski-tér O kezdőpontjában nyíllal (vektorral) ábrázolható, O jövőbe mutató fénykúpjának belsejébe (vagy a foton szélsőséges esetében a kúpra) mutat; lásd 5.36. ábra. Ez a nyíl, amely ugyanabba az irányba mutat, mint az objektum világvonala, minden információt tartalmaz energiájáról, tömegéről és impulzusáról. Így a nyíl hegyének „t értéke” (vagy „magassága”) valamely megfigyelő rendszerében mérve megadja az objektum tömegét (vagy c2-tel osztott energiáját) a megfigyelő szerint, míg a térbeli összetevő az impulzust (c-vel osztva).
E nyíl „Minkowski-hossza” a nyugalmi tömeg néven ismert, fontos mennyiség, amely a tömeget adja meg az objektumhoz képest nyugvó megfigyelő számára. Próbálkozhatnánk azzal, hogy ezt válasszuk az „anyagmennyiség” jó mértékének. Azonban nem additív: ha egy rendszer kétfelé hasad, akkor az eredeti nyugalmi tömeg nem a két új nyugalmi tömeg összege. Emlékezzünk a π0-mezon előbb vizsgált bomlására. A π0-mezon nyugalmi tömege pozitív, míg a keletkező fotonoké nulla. Az egész nyílra (négyesvektorra) azonban érvényes az additivitási tulajdonság, de most az 5.6. ábrán bemutatott vektorösszegzési szabály értelmében kell „összeadnunk”. Most ez a teljes nyíl az „anyag mennyiségére” vonatkozó mértékünk!
Gondoljunk most Maxwell elektromágneses mezőjére. Megfigyeltük, hogy energiát hordoz. Az E = mc2 szerint tömegének is kell lennie. Így Maxwell mezője szintén anyag! Ezt most biztosan el kell fogadnunk, mert a Maxwell-mezőnek szoros köze van az erőkhöz, amelyek a részecskéket összetartják. Bármely test tömegéhez lényeges járulékot107 kell adjanak a belsejében lévő elektromágneses mezők.
Mi a helyzet Einstein gravitációs mezőjével? Sok tekintetben Maxwell mezőjére emlékeztet. Hasonlóan ahhoz, ahogy Maxwell elméletében a mozgó, töltött részecskék elektromágneses hullámokat tudnak kibocsátani, a mozgó, tömeggel rendelkező testek (Einstein elmélete szerint) gravitációs hullámokat bocsátanak ki – amelyek, az elektromágneses hullámokhoz hasonlóan, a fény sebességével terjednek és energiát hordoznak. Ezt az energiát mégsem a szokásos módon, az ENERGIA tenzorral mérjük, amelyre korábban utaltam. (Tiszta) gravitációs hullámban ez a tenzor mindenhol nulla! Mindazonáltal helyezkedhetünk arra a nézőpontra, hogy valahogy a téridő görbülete (amit most teljesen a WEYL tenzor ad meg) mutathatja a gravitációs hullámok „szövedékét”. A gravitációs energia azonban nemlokális, ami azt jelenti, hogy a téridő görbületének csupán korlátos tartományban való vizsgálatával nem lehet meghatározni az energia mértékét. A gravitációs mező energiája – és ezért tömege – sikamlós angolna, nem hagyja magát egy adott helyen elcsípni. Mindazonáltal komolyan kell venni. Biztosan ott van, és számításba kell venni, hogy a tömeg általánosan megmaradhasson. Van a tömegnek egy jó (és pozitív) mértéke (Bondi 1960, Sachs 1962), amely alkalmazható a gravitációs hullámokra, de a nemlokalitás olyan, hogy ez a mérték olykor nemzérus lehet a téridő sík tartományaiban – a sugárzás két hulláma között (hasonlóan, mint a hurrikán magján belüli csend) –, ahol a téridő teljesen görbületmentes (vö. Penrose és Rindler 1986, 427. o.), azaz WEYL és RICCI egyaránt zérus! Ilyen esetekben, úgy látszik, arra kell következtetnünk, hogy ha ez a tömeg-energia egyáltalán megfogható, akkor ebben a sík üres térben kell legyen – minden anyagtól vagy mezőtől tökéletesen mentes tartományban. Ilyen furcsa körülmények között „anyagmennyiségünk” most vagy ott van az üres tartományok legüresebbjében, vagy egyáltalán nincs sehol!
Ez igazi paradoxonnak látszik. Mégis határozott velejárója annak, amit legjobb klasszikus elméleteink – és ezek valóban szuperelméletek – világunk „valóságos” anyagának természetéről mondanak. Az anyagi valóság a klasszikus elmélet szerint, nem is beszélve a kvantumelméletről, amelyet éppen kifejteni készülünk, sokkal ködösebb dolog, mint azt gondoltuk. Mennyiségi meghatározása – sőt hogy vajon ott van-e vagy sem – határozottan kényes kérdésektől függ, és nem lehet csupán lokálisan megállapítani! Ha ez a nemlokalitás rejtélyesnek látszik, akkor készüljünk fel még sokkal nagyobb megrázkódtatásokra.
...Szirénének...
6. Kvantumvarázslatok, kvantumtitkok
Kell-e a filozófusoknak a kvantumelmélet?
A klasszikus fizikában a józan ésszel összhangban „ott kint” van egy objektív világ. Ez világos és determinisztikus módon fejlődik, pontosan megfogalmazott matematikai egyenletek kormányozzák. Egyformán igaz ez Maxwell és Einstein elméleteire, és az eredeti newtoni rendszerre. A fizikai valóság tőlünk függetlenül létezik; és hogy pontosan milyen a klasszikus világ, azt nem befolyásolja az, hogy mi hogyan nézünk rá. Mi több, testünk és agyunk szintén része ennek a világnak. A klasszikus fizikában ezek is ugyanazon pontos és determinisztikus, klasszikus egyenletek szerint fejlődnek. Minden cselekedetünket ezek az egyenletek szabják meg – függetlenül attól, hogy esetleg úgy érezzük, tudatos akaratunk befolyásolhatja viselkedésünket.
Ez a kép az alapja a valóság, valamint a tudatos érzékelésünk és nyilvánvaló szabad akaratunk természetével foglalkozó legkomolyabb108 filozófiai érvrendszereknek. Egyeseknek meglehet az a kényelmetlen érzése, hogy szerepe kell legyen a kvantumelméletnek is – a dolgok ezen alapvető, de sok zavart okozó rendszerének, amely a világ tényleges viselkedése és a klasszikus fizika által szolgáltatott leírás közötti finom eltérésekből nőtt ki századunk első negyedében. A „kvantumelmélet” szó sokakban csupán egy „határozatlansági elv” homályos fogalmát ébreszti fel, amely a részecskék, atomok vagy molekulák szintjén leírásainkban megtiltja a pontosságot, csak valószínűségi viselkedést engedélyez. A kvantumos leírások, mint látni fogjuk, valójában nagyon pontosak, bár a megszokott klasszikusaktól radikálisan különböznek. Mi több, éppen egy általános nézet ellenkezőjét fogjuk találni, azt, hogy a valószínűségek nem a részecskék, atomok vagy molekulák parányi kvantumszintjén lépnek fel – azok determinisztikusam fejlődnek –, hanem látszólag valami titokzatos, nagyléptékű hatás következtében, összefüggésben a tudatosan érzékelt klasszikus világ megjelenésével. Meg kell próbálnunk megérteni ezt, és azt is, hogyan kényszerít bennünket a kvantumelmélet, hogy megváltoztassuk a fizikai valóságról alkotott képünket.
Hajlamosak vagyunk azt hinni, hogy a kvantumos és a klasszikus elméletek közötti eltérések nagyon csekélyek, ám valójában ezek állnak sok, közönséges léptékű fizikai jelenség hátterében. A szilárd testek puszta létezése, az anyagok szilárdsága és más fizikai tulajdonságai, a kémia egész természete, a tárgyak színe, a fagyás és forrás jelensége, az öröklődés megbízhatósága – és sok más megszokott tulajdonság magyarázatát a kvantumelmélet adja meg. Talán a tudatosság is olyan jelenség, amely nem érthető meg csak klasszikus fogalmak alapján. Talán értelmünk is olyan minőség, amely sokkal inkább a világunkat kormányzó fizikai törvények különös és csodálatos tulajdonságaiban gyökerezik, és nem egy klasszikus fizikai szerkezet ún. „objektumai” által végrehajtott algoritmus egy tulajdonsága. Talán bizonyos értelemben ez az, „amiért” nekünk, érző lényeknek kvantumos világban kell élnünk, és nem teljesen klasszikusban, utóbbi minden gazdagsága és igazi titokzatossága ellenére. Lehet-e olyannak megkövetelni a kvantumos világot, hogy anyagából felépíthetők legyenek gondolkodó, érző teremtmények, mint mi magunk? Ezt a kérdést sokkal inkább egy benépesített világegyetemet teremteni szándékozó Istennek kell feltenni, nem magunknak! Ám bennünket is lényegesen érint. Ha a klasszikus világnak nem lehet része a tudatosság, akkor értelmünk valamilyen módon a klasszikus fizikától való speciális eltérésekre kell hogy támaszkodjon. Erre a gondolatra később majd még visszatérek.
Ha mélyre akarunk ásni a filozófia egyes fontos kérdéseiben, akkor valóban a kvantumelmélethez – a fizikai elméletek e legegzaktjábbhoz és legtitokzatosabbjához – kell fordulnunk: hogyan viselkedik világunk, és mi alkotja az „értelmet”, amely valójában „mi” vagyunk? Mégis a tudomány egy nap majd a Természet még mélyebb megértését adhatja, mint amilyet a kvantumelmélet nyújtani tud. Személyes véleményem az, hogy még a kvantumelmélet is csak átmeneti megoldás, bizonyos lényeges dolgokban nem tud teljes képet adni világunkról, amelyben élünk. De ez nem ad felmentést; ha valamelyes filozófiai bepillantást akarunk szerezni, akkor meg kell ismernünk a világ képét a létező kvantumelmélet szerint.
Sajnos, a különböző elméletek nagyon különböző (bár a megfigyelhetőket tekintve ekvivalens) nézeteket vallanak e kép aktualitásáról. Sokan, akik a kvantumelmélet egyik központi alakját, Niels Bohrt követik, azt mondják, hogy objektív kép egyáltalán nincs is. A kvantumszinten valójában nincs semmi „ott kinn”. A valóság csak a „mérések” eredményeivel kapcsolatban merül fel. E nézet szerint a kvantumelmélet csupán számítási eljárást kínál, és nem szándékozik leírni a világot, amilyen az valójában. Az elmélethez való ilyen hozzáállás, nekem úgy tetszik, túlságosan kishitű, magam a pozitívabb vonalat követem, amely a kvantumos leírásnak objektív fizikai valóságot tulajdonít: a kvantumállapotot.
Van egy nagyon pontos egyenlet, a Schrödinger-egyenlet, amely tökéletesen determinisztikus időfejlődését adja ennek az állapotnak. Nagyon különös viszony van azonban az időfejlesztett kvantumállapot és a fizikai világ megfigyelt viselkedése között. Időről időre – amikor csak úgy véljük, hogy egy „mérés” bekövetkezett – majdnem el kell dobnunk azt a kvantumállapotot, amelyet fáradságosan fejlesztettünk, csak a különböző valószínűségek számítására használhatjuk, amelyekkel az állapot új lehetséges állapotok egy sorozatának egyikébe vagy másikába „átugrik”. E „kvantumugrás” furcsaságához jön még az a probléma, hogy meg kell határoznunk, milyen az a fizikai berendezés, amely kijelenti, hogy megtörtént egy „mérés”. A mérőkészülék maga is feltételezhetően kvantumos összetevőkből épül fel, és így a determinisztikus Schrödinger-egyenlet szerint fejlődik. Szükséges-e tudatos lény jelenléte ahhoz, hogy egy „mérés” ténylegesen megtörténjék? Azt hiszem, a kvantumfizikusoknak csak elenyésző kisebbsége felelne igennel. Feltehetően maguk az emberi megfigyelők is parányi kvantumos alkotórészekből állnak!
Itt jó pár mondatban ismerteti miről lesz szó a hatodik fejezetben…többek között:
Meg fogjuk részletesen vizsgálni a spin különös (és alapvetően kvantummechanikai) tulajdonságát. Megtárgyaljuk a „Schrödinger macskája” paradox gondolatkísérlet által felvetett fontos kérdéseket és az elméletiek különböző nézeteit, amelyek részben e nagyon alapvető rejtély megoldására irányulnak.
Spin: ott volt a negyedikes kémia könyvünkben, de én „disznó” , lusta diákként – mivel a két szaktárgyunk közül érettségire a biológiát választottam – akkor nem érdeklődtem különösebben a spin és az atomfizika iránt…
E fejezet egyes részei nem emészthetők annyira könnyen, mint az előző (vagy következő) fejezetek anyaga, és olykor kissé technikaiak. Leírásomban próbáltam nem csalni, és egy kicsit keményebben kell majd dolgoznunk, mint egyébként, hogy valamennyire megérthessük a kvantumos világot. Tanácsolom az Olvasónak, folytassa akkor is, ha egy érv homályos marad, próbáljon a szerkezet egészének ízére ráérezni. Ne keseredjen el akkor sem, ha a teljes megértés nem sikerül. Ez magának a tárgykörnek a természetéből ered!
Mint Moldova csodacsatára az Idegen bajnok-ban én is lehajolok és megkötöm rendesem a futballcipőm fűzőjét, nehogy leessen miközben megkísérlem a kissé nehéznek igérkező utolsó akciót (itt a megértést) végrehajtani.
Átmenet egyikből a másikba. Folytatás.
E fejezet egyes részei nem emészthetők annyira könnyen, mint az előző (vagy következő) fejezetek anyaga, és olykor kissé technikaiak. Leírásomban próbáltam nem csalni, és egy kicsit keményebben kell majd dolgoznunk, mint egyébként, hogy valamennyire megérthessük a kvantumos világot. Tanácsolom az Olvasónak, folytassa akkor is, ha egy érv homályos marad, próbáljon a szerkezet egészének ízére ráérezni. Ne keseredjen el akkor sem, ha a teljes megértés nem sikerül. Ez magának a tárgykörnek a természetéből ered!
Mint Moldova csodacsatára az Idegen bajnok-ban én is lehajolok és megkötöm rendesen a futballcipőm fűzőjét, nehogy leessen miközben megkísérlem a kissé nehéznek ígérkező utolsó akciót (itt a megértést) végrehajtani. -amúgy mindig is falábú voltam a fociban, soha nem voltam csodacsatár, de nagyon szerettem játszani.
Itt Penrose könyvének hatodik fejezetének tartalmáról: a kvantumfizika rejtelmeiről beszél. A klasszikus elmélet problémái
Miből tudjuk, hogy a klasszikus fizika nem írja le világunkat tökéletesen? A fő okok kísérletiek. A kvantumelméletet nem az elméletiek kínálták nekünk. Legtöbbször csak nagyon vonakodva
hagyták magukat e különös és filozófiailag sok tekintetben nem kielégítő világnézet felé vezetni. Ám a klasszikus elméletnek minden nagyszerűsége ellenére komoly nehézségei vannak. Ezek gyökere az, hogy kétfajta fizikai objektumnak kell együtt léteznie: véges, kisszámú (három hely, három impulzus) paraméterrel leírt részecskéknek és végtelen számú paramétert igénylő mezőknek. Ez a kettéosztás fizikailag nem igazán következetes. Egy rendszerben, amelyben részecskék és mezők is vannak, egyensúlyban (azaz „teljesen megállapodottan”) minden energia átmegy a részecskékből a mezőkbe. Ez az „energia ekvipartíciójának” nevezett jelenség eredménye: egyensúlyban az energia egyenletesen oszlik meg a rendszer szabadsági fokai között. Mivel a mezőknek végtelen sok szabadsági foka van, szegény részecskéknek nem marad semmi!
Speciálisan, a klasszikus atomok nem lennének stabilisak, a részecskék minden mozgása átvivődne a mezők hullámmódusaiba. Idézzük fel az atom „naprendszer”-modelljét, ahogy azt 1911-ben a kiváló új-zélandi–brit kísérleti fizikus, Ernest Rutherford kidolgozta. A bolygók helyében a keringő elektronok, a Nap helyében a központi atommag – a lépték parányi –, s nem a gravitáció, hanem az elektromágnesség tartja össze e rendszert. Alapvető és látszólag leküzdhetetlen probléma, hogy a mag körül keringő elektronnak a Maxwell-egyenletek szerint elektromágneses hullámokat kell kibocsátania, amelyek intenzitása gyorsan, egy másodperc kis töredéke alatt végtelenre nő, ahogy az elektron spirális pályán belezuhan a magba! Ám semmi ilyet nem figyelünk meg. Amit ténylegesen megfigyelünk, az a klasszikus elmélet alapján megmagyarázhatatlan. Az atomok ki tudnak bocsátani elektromágneses hullámokat (fényt), de csak nagyon speciális, diszkrét frekvenciájú adagokban – ezek eredményezik a megfigyelt éles színképvonalakat (6.1. ábra). Mi több, ezek a frekvenciák „örült” szabályokat109 elégítenek ki, amelyeknek a klasszikus elméletben semmiféle alapjuk nincsen.
Speciálisan, a klasszikus atomok nem lennének stabilisak, a részecskék minden mozgása átvivődne a mezők hullámmódusaiba. Idézzük fel az atom „naprendszer”-modelljét, ahogy azt 1911-ben a kiváló új-zélandi–brit kísérleti fizikus, Ernest Rutherford kidolgozta. A bolygók helyében a keringő elektronok, a Nap helyében a központi atommag – a lépték parányi –, s nem a gravitáció, hanem az elektromágnesség tartja össze e rendszert. Alapvető és látszólag leküzdhetetlen probléma, hogy a mag körül keringő elektronnak a Maxwell-egyenletek szerint elektromágneses hullámokat kell kibocsátania, amelyek intenzitása gyorsan, egy másodperc kis töredéke alatt végtelenre nő, ahogy az elektron spirális pályán belezuhan a magba! Ám semmi ilyet nem figyelünk meg. Amit ténylegesen megfigyelünk, az a klasszikus elmélet alapján megmagyarázhatatlan. Az atomok ki tudnak bocsátani elektromágneses hullámokat (fényt), de csak nagyon speciális, diszkrét frekvenciájú adagokban – ezek eredményezik a megfigyelt éles színképvonalakat (6.1. ábra). Mi több, ezek a frekvenciák „örült” szabályokat109 elégítenek ki, amelyeknek a klasszikus elméletben semmiféle alapjuk nincsen.
A mezők és részecskék instabil együttélésének egy másik megnyilvánulása a „feketetest-sugárzás” néven ismert jelenség. Képzeljünk el egy határozott hőmérsékletű objektumot, amikor az elektromágneses sugárzás egyensúlyban van a részecskékkel. Rayleigh és Jeans 1900-ben kiszámították, hogy ekkor a mezők minden energiát felszívnának – korlát nélkül! Ez fizikai abszurditást foglal magában (az „ultraibolya-katasztrófát”: az energia folyamatosan megy át a mezőkbe, egyre magasabb frekvenciák felé, megállás nélkül), ám a Természet sokkal óvatosabban viselkedik. A mezők alacsony frekvenciájú oszcillációiban az energia tényleg annyi, ahogy Rayleigh és Jeans azt megjósolták, de a magas frekvenciáknál, ahol ők katasztrófát jósoltak, a megfigyelések azt mutatják, hogy az energia nem növekszik korlátlanul, hanem a frekvencia növekedésével nullához tart. Az energia a legnagyobb értéket adott hőmérséklet mellett egy nagyon speciális frekvencián (azaz színnél) veszi fel (lásd 6.2. ábra). (A piszkavas piros vagy a Nap sárgásfehér izzása két közismert példája ennek.)
A kvantumelmélet kezdetei
Mi a megoldásuk ezeknek a rejtélyeknek? A részecskék eredeti newtoni rendszerét biztosan ki kell egészíteni a Maxwell-féle mezőkkel. Elmehetünk-e a másik szélsőségig, feltételezve, hogy minden, ami van, mező, és a részecskék egyfajta mező kis, véges méretű „csomói”? Ennek is vannak nehézségei, mert a részecskék így egyfolytában változtatnák alakjukat, végtelen sok különböző módon tekergőznének és rezegnének. Azonban nem ezt látjuk. A fizikai világban az ugyanolyan típusú részecskék azonosaknak látszanak. Például bármely két elektron ugyanolyan. Még az atomoknak és molekuláknak is csak diszkréten különböző elrendezéseik lehetnek.110 Ha a részecskék mezők, akkor valami új elemre van szükség, amely a mezőket diszkrét jellemzőkkel ruházza fel.
1900-ban a ragyogó, de konzervatív és óvatos német fizikus, Max Planck forradalmi elképzeléssel állt elő a nagyfrekvenciás „feketetest”-módusok elnyomására: az elektromágneses rezgések csak „kvantumokban” mennek végbe, amelyek E energiája határozott viszonyban van a v frekvenciával,
E = hv,
Hogy lehet az, hogy a fény egyszerre tartalmaz részecskéket és mezőrezgéseket? Ez a két fogalom kibékíthetetlenül ellentmondásosnak látszik. Egyes kísérleti tények mégis világosan jelzik, hogy a fény részecskékből áll, mások pedig azt, hogy hullámokból. 1923-ban a francia arisztokrata és ötletdús fizikus, Louis de Broglie herceg egy lépéssel továbbvitte ezt a részecske–hullám kettősséget, amikor
azt javasolta, hogy maguk az anyag részecskéi olykor hullámként viselkednek! Az általa javasolt v hullámfrekvencia tetszőleges m tömegű részecskére eleget tesz a Planck-összefüggésnek. Összekapcsolva az Einstein-féle E = mc2 egyenlőséggel megkapjuk v és m viszonyát:
hv = E = mc2.
De Broglie javaslata szerint tehát a részecskék és mezők kettéosztottságát, ami a klasszikus elmélet egy tulajdonsága volt, a Természet nem méltányolja! Bármi, ami v frekvenciával rezeg, csak diszkrét hv/c2 tömegegységekben fordulhat elő. A Természet valahogyan kitalálta, hogyan építsen fel olyan konzisztens világot, amelyben a részecskék és a mezőrezgések ugyanazt a dolgot jelentik! Vagy másképp szólva a világ finomabb alkotórészekből áll, amelyekre a „részecske” és „hullám” megjelölés csak részben megfelelő.
A Planck-összefüggés egy másik gyönyörű alkalmazása Niels Bohr dán fizikustól, a 20. század tudományos gondolkodásának kiemelkedő alakjától származik (1913-ból). Bohr szabályai megkövetelték, hogy az atommag körül keringő elektronok impulzusmomentuma (lásd 5. fejezet) csak h/2π egész számú többszöröse lehessen, erre vezette be később Dirac a hagyományos ħ szimbólumot:
ħ = h/2π.
Így az (egy tengely körüli) impulzusmomentum megengedett értékei:
0, ħ, 2ħ, 3ħ, 4ħ, … .
Az atom „naprendszer”-modellje ezzel az új elemmel igen pontosan megadott sok diszkrét, stabil energiaszintet és „őrült” szabályt a színkép frekvenciáira, amelyeknek a Természet ténylegesen engedelmeskedik!
Bohr-elmélete még nem volt az „igazi”, írja Penrose; ugyanakkor Heisenberg: Rész és egész c. önéletrajzi írásában Bohrt az elmélet kidolgozói, kutatói között a kérdéskör egyik főszereplőjeként mutatja be; akinek dániai otthonában sokszor összegyűltek a fizikusok: és hideg őszi vagy téli estéken – forró teát kortyolgatva - hosszú vitákat folytattak a témában felmerülő megoldatlanságokról, ellentmondásokról, rejtélyekről. Ugyanezt persze máshol, a más helyszíneken, más országokban rendezett kongresszusokon, vagy egyetemi előadások után is megtették.
A ma ismert kvantumelmélet két későbbi, egymástól független elgondolásból nőtt ki, amelyek szerzője két neves fizikus: a német Werner Heisenberg és az osztrák Erwin Schrödinger. A két rendszer (az 1925-ös „mátrixmechanika” és az 1926-os „hullámmechanika”) először egészen különbözőnek látszott, de hamarosan megmutatkozott, hogy egyenértékűek, és egy átfogóbb és általánosabb keretben egyesítették azokat, elsősorban a kitűnő brit elméleti fizikus, Paul Adrien Maurice Dirac.
A kétrés-kísérlet
Nézzük a kvantummechanikai kísérletek „mintapéldányát”, amelyben egy elektronnyaláb vagy fény, vagy másfajta „részecske–hullám” egy szűk réspáron áthaladva jut a rések mögött elhelyezett ernyőre (6.3. ábra). A határozottság kedvéért válasszuk a fényt, és a szokásos terminológiának megfelelően nevezzük a fénykvantumokat „fotonoknak”. A fény legvilágosabb részecskemegnyilvánulása (azaz a fotonok) a képernyőn látható. Ide diszkrét, lokalizált energiaegységekben érkezik, amelynek nagysága és a fény frekvenciája között változatlanul fennáll a Planck-féle kapcsolat: E = hv. Az energia soha nem „fele” (vagy másféle töredéke) egy fotonnak. A fény beérkezése fotonegységekben „minden vagy semmi” jelenség. Mindig csak egész számú fotont lehet látni.
Azonban hullámszerű viselkedés figyelhető meg, amikor a fotonok keresztülhaladnak a réseken. Tegyük fel először, hogy csak az egyik rés van nyitva (a másikat lezártuk). Áthaladás után a fény szétterjed – ez a diffrakció jelensége, a hullámterjedés egyik tulajdonsága. De kitarthatunk még a részecskekép mellett, és azt képzelhetjük, hogy a rés széleinek közelsége fejt ki valamilyen hatást a fotonokra, és azok véletlenszerűen térülnek el egyik vagy másik irányban. Amikor a fény intenzitása, azaz a fotonok száma elég nagy, akkor az ernyő megvilágítása nagyon egyenletesnek látszik. Ám ha lecsökkentjük az intenzitást, akkor meggyőződhetünk arról, hogy a megvilágítás eloszlása egyedi pontokból tevődik össze, ezekben a pontokban csapódnak be az egyedi fotonok az ernyőre – a részecskeképpel összhangban. A megvilágítás egyenletessége statisztikus jelenség, a fotonok nagyon nagy számának következménye (lásd 6.4. ábra). (Összehasonlításképpen: egy 60 wattos égő másodpercenként kb. 100 000 000 000 000 000 000 fotont bocsát ki!) A fotonok valóban valamilyen véletlenszerű módon látszanak eltérülni, mikor áthaladnak a résen – a különböző szögekben különböző valószínűségekkel, ami a megvilágítás megfigyelt eloszlását eredményezi.
A részecskekép fő problémájával azonban akkor kerülünk szembe, amikor kinyitjuk a másik rést! Tegyük fel, hogy a fény egy sárga nátriumlámpából jön, tehát lényegében tiszta, nem kevert színű – szakkifejezéssel monokromatikus, azaz egy meghatározott hullámhosszt vagy frekvenciát tartalmaz, ami a részecskeképben azt jelenti, hogy minden foton azonos energiájú. Ez a hullámhossz kb. 5 ∙ 10–7 m. Vegyük a rések szélességét kb. 0,001 mm-re, távolságukat kb. 0,15 mm-re, és az ernyő legyen kb. egy méternyire. Ésszerűen erős intenzitás mellett még mindig szabályosnak látszó megvilágításeloszlást kapunk, de most valamiféle hullámosság jelentkezik, amit interferenciaképnek neveznek, az ernyőn kb. három milliméter széles sávok láthatók a középvonalra szimmetrikusan (6.5. ábra). Azt várhattuk, hogy a második rés megnyitása egyszerűen megkétszerezi az ernyő megvilágításának erősségét. Ám az intenzitás részletes mintázata most tökéletesen különbözik attól, amit egyetlen résnél láttunk. Az ernyő egyes pontjaiban – ahol a minta a legfényesebb – a megvilágítás erőssége nem kétszerese, hanem négyszerese a korábbinak. Más pontokban – ahol a minta a legsötétebb – az intenzitás nullára csökkent. Talán ez jelenti a legnagyobb rejtélyt a részecskekép számára. Amikor csak egy rés volt nyitva, akkor a fotonok vidáman beérkeztek ezekbe a pontokba. Most, hogy kinyitottuk a másikat is, hirtelen valami megakadályozza őket, hogy azt csinálják, amit előbb csináltak. Hogyan lehetséges az, hogy amikor egy alternatív utat nyitunk számukra, akkor valójában mindkettőt elzárjuk előlük?
A foton skáláján, ha „méretének” a hullámhosszát vesszük, a második rés úgy 300 „fotonnyira” van az elsőtől (mindkettő egy pár hullámhossznyi széles) (lásd a 6.6. ábrát). Hogyan „tudhatja” akkor a foton, amikor áthalad az egyik résen, hogy a másik éppen nyitva van-e vagy sem? E „kioltó” vagy „erősítő” jelenség elvileg a két rés akármilyen távolsága mellett bekövetkezhet.
Amint a fény keresztüljut a rés(ek)en, úgy látszik, nem részecske, hanem hullám módjára viselkedik! Az ilyen kioltás – a destruktív interferencia – a közönséges hullámok megszokott tulajdonsága. Ha a hullám két úton külön-külön végigmehet, és ha mindkettő nyitva van számára, akkor nyugodtan előfordulhat, hogy kioltja saját magát. A 6.7. ábrán vázoltam, hogyan következik ez be. Ha a hullámnak az egyik résen áthaladó egy adagja találkozik a másikon áthaladó egy adagjával, akkor, ha „fázisban” vannak (azaz, ha hullámhegy hullámheggyel, hullámvölgy hullámvölggyel találkozik), erősítik, de ha pontosan ellentétes fázisban találkoznak (hullámhegy hullámvölggyel), akkor kioltják egymást. A kétrés-kísérletnél az ernyő fényes sávjai ott jönnek létre, ahol a két réstől mért távolságok különbsége a hullámhossz egész számú többszöröse, tehát hegy valóban heggyel, völgy völggyel találkozik, sötét rész pedig ott, ahol a két távolság különbsége pontosan az előző értékek fele, tehát hegy völggyel, völgy heggyel találkozik.
Abban semmi rejtélyes nincs, hogy egy közönséges, makroszkopikus, klasszikus hullám egyszerre két résen halad keresztül a leírt módon. Egy hullám végül is vagy valamilyen folytonos közeg (mező), vagy apró pontszerű részecskék miriádjaiból állóanyag egy „zavara”. A zavar áthaladhat részben az egyik, részben a másik résen. De most a helyzet egészen más: az összes egyedi foton pusztán önmagában viselkedik hullámként! Valamilyen értelemben mindegyik részecske áthalad egyszerre mindkét résen, és önmagával interferál! A fény teljes intenzitását elegendően lecsökkentve biztosíthatjuk, hogy egy időben csak egyetlen foton legyen a rések szomszédságában. A destruktív interferencia jelensége, amikor a foton számára lehetséges két alternatív út valahogyan megsemmisíti egymást mint lehetőséget, egyetlen foton esetében is megvalósul. Ha a két út közül csak az egyik van nyitva a foton előtt, akkor a foton ezen végigmehet. Ha csak a másik van nyitva, akkor azon is végigmehet. De ha mindkettő nyitva van, akkor a két lehetőség varázslatos módon megsemmisíti egymást, és a foton, úgy látszik, egyiken sem képes átjutni!
Tartson az Olvasó egy kis szünetet, hogy felfogja e rendkívüli tény jelentését. Nem az a helyzet, hogy a fény olykor részecskeként, olykor hullámként viselkedik. A dolog úgy néz ki, hogy minden egyes részecske teljesen önmagában viselkedik hullámszerűén; és az egy részecske számára nyitva álló, különböző alternatív lehetőségek olykor képesek megsemmisíteni egymást!
Ténylegesen kettéhasad a foton, és az egyik rész az egyik, a másik rész a másik résen megy át? A legtöbb fizikus ellenezné a dolgok ilyen megfogalmazását. Kitartanának amellett, hogy noha mindkét, a részecske számára nyitott út hozzá kell járuljon a végső jelenséghez, ezek akkor is alternatív utak, és nem szabad azt gondolni, hogy a részecske két részre hasad, hogy átjusson a réseken. Támogatandó azt a nézetet, hogy a részecske nem részben az egyik, részben a másik résen halad át, a kísérletet úgy módosíthatjuk, hogy az egyik vagy a másik réshez egy részecskedetektort helyezünk. Mivel megfigyeléskor a foton – vagy bármelyik más részecske – mindig egyetlen egésznek mutatkozik, tört résznek soha, ezért detektorunknak is vagy egy egész fotont kell észlelnie, vagy semmit. Ám amikor detektor van az egyik résnél, tehát a megfigyelő meg tudja mondani, melyik résen ment a foton át, akkor az ernyőről a hullámos interferenciarajzolat eltűnik. Hogy interferencia legyen, ahhoz láthatóan szükséges a „tudás hiánya” arról, hogy a részecske „ténylegesen” melyik résen ment keresztül.
Az interferenciához mindkét lehetőségnek hozzá kell járulnia, néha „összeadódva”: kétszer annyira erősítve egymást, mint ahogy várnánk –, néha „kivonódva”: úgy, hogy a lehetőségek rejtélyesen „megsemmisíthetik” egymást. Ami a kvantummechanika szabályai szerint ténylegesen történik, az ennél még rejtélyesebb! A lehetőségek valóban összeadódhatnak (az ernyő legfényesebb pontjai), és valóban kivonódhatnak (sötét pontok); de más furcsa kombinációkká is összeállhatnak (az ernyő közepes intenzitású pontjaiban), mint például
„A lehetőség” + i × „B lehetőség”,
ahol „i” a „mínusz egy négyzetgyöke”=
amivel a 3. fejezetben találkoztunk. Valójában tetszőleges komplex szám betölthet ilyen szerepet a „lehetőségek kombinációjában”!
Az Olvasó emlékezhet a 3. fejezetben tett figyelmeztetésemre, hogy a komplex számok „abszolút alapvetőek a kvantummechanika szerkezetében”. E számok nem csak matematikai szépségek. Váratlan, de meggyőző kísérleti tényeken keresztül felhívták magukra a fizikusok figyelmét. Hogy a kvantummechanikát megértsük, meg kell barátkoznunk a komplex számokkal való súlyozással.
Valószínűségi amplitúdók
Semmi egyedi nincs abban, hogy a fenti leírásban fotonokat használtunk. Elektronok vagy másfajta részecskék, akár egész atomok ugyanúgy megteszik. A kvantummechanika szabályai, úgy tetszik, még a krikettlabdákra és az elefántokra is ugyanezt a különös viselkedést írják elő, amelyben a különböző alternatív lehetőségek valamilyen módon komplexszám-kombinációkban „adódhatnak össze”! Azonban soha nem látunk krikettlabdákat vagy elefántokat ilyen furcsán szuperponálódni. Miért nem? Ez nehéz, sőt vitatott kérdés, és egyelőre nem kívánok belemélyedni. Egyelőre mint munkaszabályt egyszerűen feltételezzük, hogy a fizikai leírásnak két különböző lehetséges szintje van, a kvantumszint és a klasszikus szint. A furcsa komplexszám-kombinációkat csak a kvantumszinten fogjuk használni. A krikettlabdák és elefántok klasszikus objektumok.
A kvantumszint a molekulák, atomok, szubatomi részecskék stb. szintje. Általában úgy gondolunk rá, mint a nagyon „kis skálájú” jelenségek szintjére, de ez a „kicsiség” valójában nem a fizikai méretre vonatkozik. Látni fogjuk, hogy a kvantumos jelenségek sok méteres, sőt fényéves távolságokon is megjelenhetnek. Valamivel közelebb van az igazsághoz, ha akkor tekintünk valamit a „kvantumszinten” lévőnek, ha csak nagyon kis energiakülönbségek fordulnak elő benne. (Később, főként a 8. fejezetben majd megpróbálok pontosabban fogalmazni.) A klasszikus szint az a „makroszkopikus” szint, amelyről közvetlen tudomásunk van. Ez az, ahol a „dolgok történéséről” alkotott közönséges képünk érvényes, ahol használhatjuk szokásos valószínűségi elképzeléseinket. Látni fogjuk, hogy a komplex számok, amelyeket a kvantumszinten használnunk kell, közeli kapcsolatban állnak a klasszikus valószínűségekkel. Nem igazán azonosak, de hogy megbarátkozzunk velük, érdemes lesz először azt felidéznünk, hogyan viselkednek a klasszikus valószínűségek.
Tekintsünk egy klasszikus helyzetet, amely bizonytalan, tehát nem tudjuk, hogy az A vagy B lehetőségek melyike következik be. A helyzetet ezen alternatívák „súlyozott” kombinációjával lehet leírni:
p × „A lehetőség” + q × „B lehetőség”,
ahol p az A lehetőség, q a B lehetőség valószínűsége. (Emlékezzünk rá, hogy a valószínűség egy 0 és 1 közé eső valós szám. Az 1 valószínűség azt jelenti, hogy „biztosan megtörténik”, a 0 azt, hogy „biztosan nem történik meg”. 1/2 a valószínűség akkor, ha „egyformán valószínű, hogy megtörténik és hogy nem”.) Ha más lehetőség, mint A és B, nincs, akkor a két valószínűség összegének 1-nek kell lennie:
p + q = 1.
Ha azonban vannak további lehetőségek, akkor az összeg kisebb lehet 1-nél. Ekkor a p : q arány az A és B bekövetkezési valószínűségeinek az aránya. A tényleges valószínűségek, ha tudjuk, hogy a két esemény valamelyike bekövetkezik, p/(p + q) és q/(p + q). Ezt az értelmezést akkor is használhatjuk, ha p + q nagyobb, mint 1. (Ez hasznos lehet például akkor, amikor egy kísérletet sokszor megismétlünk, és p-szer fordul elő az A esemény, q-szor a B esemény.) Azt mondjuk, hogy p és q normáltak, ha p + q = 1, tehát megadják a tényleges valószínűségeket, nem csak azok hányadosát.
A kvantumfizikában csinálunk majd valamit, ami nagyon hasonlónak látszik ehhez, csak p és q most komplex számok – amelyeket jobban szeretek w-vel és z-vel jelölni:
w × „A lehetőség” + z × „B lehetőség”.
Hogyan értelmezzük w-t és z-t? Biztosan nem közönséges valószínűségek (vagy azok hányadosai), mert mindegyik lehet negatív vagy komplex, de sok tekintetben a valószínűségekhez hasonlóan viselkednek. Valószínűségi amplitúdóknak nevezzük őket (megfelelő normálás esetén – lásd később), vagy egyszerűen amplitúdóknak. Mi több, gyakran használjuk azt a terminológiát, amelyet a valószínűségek sugallnak: „w amplitúdója van annak, hogy A bekövetkezik, és z amplitúdója annak, hogy B bekövetkezik”. Nem valószínűségek, de egyelőre megpróbálunk úgy tenni, mintha azok volnának – vagy inkább a valószínűségek analogonjai a kvantumszinten.
Hogyan működnek a közönséges valószínűségek? Segíteni fog, ha egy makroszkopikus objektumra, mondjuk egy golyóra gondolunk, amelyet két lyuk valamelyikén át az utánuk elhelyezett ernyő felé ütünk – mint az előbb leírt kétrés-kísérletben (vö. 6.3. ábra), de most egy klasszikus, makroszkopikus golyó helyettesíti az előző kísérlet fotonját. Van valamekkora P(F, Rf) valószínűsége annak, hogy a golyó F-ből indítva a felső Rf lyukat éri el, és valamekkora P(F, Rf) valószínűsége annak, hogy az alsó Ra lyukat. Kiválasztunk továbbá az ernyőn egy E pontot; P(Rf, E) a valószínűsége annak, hogy a golyó Rf-en átmenve az ernyő E pontjába jut, és P(Ra, E) a valószínűsége annak, hogy Ra-n átmenve jut az E pontba. Ha csak a felső Rf lyuk van nyitva, akkor annak valószínűségét, hogy a golyó indítás után Rf-n keresztül eléri E-t, úgy kapjuk meg, hogy az F-ből Rf-be jutás valószínűségét megszorozzuk az Rf-ből E-be jutás valószínűségével:
P(F, Rf) ∙ P(Rf, E).
Hasonlóan, ha csak az alsó lyuk van nyitva, akkor annak valószínűsége, hogy a golyó F-ből E-be jut:
P(F, Ra) ∙ P(Ra, E).
Ha mindkét lyuk nyitva van, akkor az F-ből Rf-en keresztül E-be jutás valószínűsége továbbra is az első kifejezés, P(F, Rf) ∙ P(Rf, E), mintha csak Rf volna nyitva, és az F-ből Ra-n keresztül E-be jutás valószínűsége továbbra is P(F, Ra) P(Ra, E), így annak teljes P(F, E) valószínűsége, hogy F-ből E-be jut, e kettő összege:
P(F, E) = P(F, Rf) ∙ P(Rf, E) + P(F, Ra) ∙ P(Ra, E).
A kvantumszinten a szabályok pontosan ugyanezek, csak ott ezek a furcsa komplex amplitúdók kell játsszák az előbbi valószínűségek szerepét. Így a kétrés-kísérletben van egy A(F, Rf) amplitúdónk arra, hogy a foton az F forrásból elérje a felső Rf rést, és egy A(Rf, E) amplitúdónk arra, hogy a Rf réstől elérje az ernyő E pontját. Ezeket összeszorozva kapjuk annak
A(F, Rf) ∙ A(Rf, E)
amplitúdóját, hogy a foton Rf-n keresztül az ernyő E pontjába jut. Mint a valószínűségeknél, ez a helyes amplitúdó, feltéve hogy a felső rés nyitva van, és függetlenül attól, hogy az alsó Ra rés nyitva van-e vagy sem. Hasonlóképpen, feltéve hogy Ra nyitott, van egy
A(F, Ra) ∙ A(Ra, E)
amplitúdója annak, hogy a foton F-ből Ra-n keresztül eljut E-be (akár nyitva van Rf, akár nincs). Ha mindkét rés nyitva van, akkor
A(F, E) = A(F, Rf) ∙ A(Rf, E) + A(F, Ra) ∙ A(Ra, E)
a teljes amplitúdója annak, hogy a foton F-ből E-be jut.
Ez mind nagyon szép, de sok haszna nincs addig, amíg nem tudjuk, hogyan értelmezzük ezeket az amplitúdókat, amikor egy kvantumos jelenség felnagyítva eléri a klasszikus szintet. Lehet például E-ben egy fotondetektor vagy fotocella, amely módot ad arra, hogy egy kvantumos szintű eseményt – egy foton E-be érkezését – klasszikusan észrevehető eseménnyé, mondjuk egy hallható „kattanássá” erősítsük fel. (Ha az ernyő fotolemezként működik, vagyis ha a fotonok látható pontokat hagynak rajta, akkor ez éppen olyan jó, de a világosság kedvéért maradjunk a fotocellánál.) A „kattanás” bekövetkeztének is kell legyen egy aktuális valószínűsége, amely nem ezen titokzatos „amplitúdók” valamelyike. Hogyan jutunk el az amplitúdóktól a valószínűségekig, amikor a kvantumosról átmegyünk a klasszikus szintre? Kiderül, hogy erre van egy nagyon szép, de titokzatos szabály.
A szabály az, hogy a komplex kvantumamplitúdó abszolútérték-négyzetét kell vennünk, hogy megkapjuk a klasszikus valószínűséget. Mi az „abszolútérték-négyzet”? Emlékezzünk a komplex számok leírására az Argand-síkon (3. fejezet). Egy z komplex szám |z| abszolút értéke a z által leírt pont távolsága a kezdőponttól (azaz a 0 ponttól). A |z|2 abszolútérték-négyzet e szám négyzete. Így ha
z = x + iy,
ahol x és y valós számok, akkor (a Pitagorasz-tétel szerint, mert a 0-tól z-ig húzott szakasz a 0, x, z derékszögű háromszög átfogója) a keresett abszolútérték-négyzet
|z|2 = x2 + y2.
Jegyezzük meg, hogy ez akkor valódi „normált” valószínűség, ha a |z|2 értéke 0 és 1 közé esik. Ez azt jelenti, hogy egy helyesen normált amplitúdónál a z pontnak az Argand-síkon az egységkörben kell feküdnie (lásd 6.8. ábra). Olykor azonban a
w × „A lehetőség” + z × „B lehetőség”
kombinációt akarjuk vizsgálni, ahol w és z csupán arányosak a valószínűségi amplitúdókkal, és nem kell e körben feküdniük. Annak feltétele, hogy normáltak (és így igazi valószínűségi amplitúdók) legyenek, az, hogy abszolútérték-négyzeteik összege az egység legyen:
|w|2 + |z|2 = 1.
Ha w és z nem így normáltak, akkor A és B tényleges amplitúdója rendre
, ezek az egységkörben fekszenek.
Lehet, hogy túl sok mindezt idemásolnom a könyvből, de a hatodik fejezet néhány alfejezete, például ez is, közelebb hozzák a megértés esélyét (számomra), mert ezekből geometriai ábrázolásokon keresztül szemléletesebbé válhat a szavakkal megfoghatatlan.
A valószínűség számítást negyedikben tanultuk; a komplex számokkal azonban ott nem találkoztunk.
Még lesz egy-két ilyen alfejezet: ilyen túl sok a jóból. Amikor végére érek Penrose könyvének,
akkor megpróbálom ezt a két vagy három folytatásban közölt bejegyzést egy kis rostálással összefűzni. Ezek a folytatások: vázlatok, feljegyzések az egyelőre még csak sejtett egész mozaikdarabjai. „Rész és egész”
Látjuk most, hogy egy valószínűségi amplitúdó nem igazán valószínűség, sokkal inkább egy valószínűség „komplex négyzetgyöke”. Hogyan érinti ez a dolgokat, amikor a kvantumszintű jelenségek felnagyítódnak a klasszikus szintre? Emlékezzünk arra, hogy a valószínűségek és amplitúdók kezelésénél olykor meg kell szoroznunk vagy össze kell adnunk azokat. Először azt kell megjegyeznünk, hogy a szorzás művelete nem jelent problémát a kvantumosról a klasszikus szabályokra való áttérésnél. Ez annak a figyelemre méltó matematikai ténynek a következménye, hogy két komplex szám szorzatának abszolútérték-négyzete egyenlő abszolútérték-négyzeteik szorzatával:
|zw|2 = |z|2|w|2.
(Ez a tulajdonság azonnal következik két komplex szám szorzatának a 3. fejezetben bemutatott geometriai leírásából; de a z = x + iy, w = u + iv valós és képzetes részeivel kifejezve csinos kis bűvészkedés. Tessék kipróbálni!)
E ténynek az a velejárója, hogy ha a részecske előtt csak egyetlen út, például a kétrés-kísérletben csak egyetlen rés (mondjuk az Rf) van nyitva, akkor „klasszikusan” lehet érvelni, és a valószínűségek ugyanazok, függetlenül attól, hogy detektáljuk-e a részecskét egy további, közbeeső pontban (Rf-nél).111 Az abszolútérték-négyzeteket vehetjük mindkét lépcsőben vagy csak a végén, például
|A(F, Rf)|2 ∙ |A(Rf, E)|2 = |A(F, Rf) ∙ A(Rf, E)|2,
az eredő valószínűség mindkét esetben ugyanaz lesz.
Ha azonban egynél több út járható (például mindkét rés nyitva van), akkor összeget kell képeznünk, és itt kezdenek mutatkozni a kvantummechanika jellegzetes sajátosságai. Amikor a w és z komplex számok w + z összegének abszolútérték-négyzetét képezzük, akkor általában nem abszolút értékeik négyzetösszegét kapjuk; van egy további „korrekciós tag”:
|w + z|2 = |w|2 + |z|2 + 2|w||z| cosθ.
Itt θ a z és w pontoknak az Argand-sík kezdőpontjánál bezárt szöge (lásd 6.9. ábra). (Emlékezzünk rá, hogy egy szög koszinusza a „szög mellett fekvő befogó/átfogó” hányados egy derékszögű háromszögben. A fenti képletet nem ismerő, lelkes Olvasó közvetlenül levezetheti azt a 3. fejezetben bevezetett geometria segítségével. E képlet valójában nem más, mint az ismerős „koszinusztétel” kicsit álcázva!) A 2|w||z| cosθ korrekciós tag eredményezi a kvantuminterferenciát a kvantummechanikai alternatívák között. A cosθ kifejezés értéke –1 és 1 közé eshet. Amikor θ = 0°, akkor cosθ = 1, és a két lehetőség erősíti egymást, így a teljes valószínűség nagyobb, mint az egyes valószínűségek összege. Amikor θ = 180°, akkor cosθ = –1, és a két lehetőség ki akarja oltani egymást, ekkor a teljes valószínűség kisebb, mint az egyes valószínűségek összege (destruktív interferencia). Amikor θ = 90°, akkor cosθ = 0, ekkor az a köztes helyzet áll elő, amikor a két valószínűség összeadódik. Nagy vagy bonyolult rendszereknél a korrekciós tagok általában „kiátlagolódnak” – mert cosθ „átlagos” értéke nulla –, és megkapjuk a klasszikus valószínűségek közönséges szabályát! A kvantumszinten azonban ezek a tagok fontos interferenciajelenségeket eredményeznek.
Tekintsük a kétrés-kísérletet, amikor mindkét rés nyitva van. Annak amplitúdója, hogy a foton elérje E-t, egy összeg, w + z, ahol most
w = A(F, Rf) ∙ A(Rf, E), | z = A(F, Ra) ∙ A(Ra, E). |
Az ernyő legfényesebb pontjában w = z (tehát cosθ = 1), ebből
|w + z|2 = |2w|2 = 4|w|2,
ez négyszerese a |w|2 valószínűségnek, amely akkor érvényes, ha csak a felső rés van nyitva – és ezért négyszerese az intenzitásnak, amikor nagyszámú foton van jelen, egyezésben a megfigyeléssel. Az ernyő sötét pontjaiban w = –z (tehát cosθ = –1), amiből
|w + z|2 = |w – w|2 = 0,
azaz zérussal egyenlő (destruktív interferencia), ismét egyezésben a megfigyeléssel. Az egzaktul közbenső pontoknál w = iz vagy w = –iz (tehát cosθ = 0), ebből
|w + z|2 = |w ± iw|2 = |w|2 + |w|2 = 2|w|2,
az intenzitás kétszer akkora, mint egy rés esetén (ami a klasszikus részecskék esete volna). A következő fejezet végén látni fogjuk, hogyan kell kiszámítani, ténylegesen hol vannak a fényes, sötét és közbeeső helyek.
Egy végső megjegyzést kell még tennünk. Ha mindkét rés nyitva van, akkor annak amplitúdója, hogy a részecske Rf-en keresztül eljut E-be valóban w = A (F, Rf) ∙ A(Rf, E), de ennek |w|2 abszolútérték-négyzetét nem értelmezhetjük annak valószínűségeként, hogy a részecske „ténylegesen” áthaladt a felső résen, hogy elérje E-t. Ez értelmetlenséget adna, különösen ha E az ernyő egy sötét pontja. De ha úgy döntünk, hogy „detektáljuk” a foton jelenlétét Rf-nél, ottani jelenlétének (vagy hiányának) jelenségét a klasszikus szintre felnagyítva, akkor használhatjuk |A(F, Rf)|2-et annak valószínűségeként, hogy a foton ténylegesen jelen volt Rf-nél. Ám ez a detektálás elmossa a hullámos mintát. Hogy interferencia legyen, biztosítanunk kell, hogy a foton áthaladása a réseken a kvantumszinten maradjon, vagyis mindkét alternatív út adjon járulékot, és olykor megsemmisíthessék egymást. A kvantumszinten az egyedi alternatív utaknak csak amplitúdói vannak, valószínűségei nincsenek.
111 A detektálást úgy kell végezni, hogy ne zavarja a részecske áthaladását Rf-en. Ez elérhető úgy, hogy a többi helyre rakunk detektorokat F köré, és az Rf-en való áthaladásra abból következtetünk, hogy ezek a detektorok nem szólalnak meg!
A határozatlansági elv
A legtöbb Olvasó már biztosan hallott a Heisenberg-féle határozatlansági elvről. Eszerint nem lehetséges egyidejűleg pontosan mérni (azaz a klasszikus szintre felnagyítani) egy részecske helyzetét és impulzusát. Ennél még rosszabb, hogy a pontosságok, mondjuk ∆x és ∆p szorzatára abszolút korlát létezik, amit a
∆x∆p ≥ ħ
összefüggés fejez ki. Ez azt mondja, hogy minél pontosabban mérjük az x helyzetet, annál kevésbé pontosan lehet a p impulzust meghatározni és viszont. Ha a helyzetet végtelen pontossággal mérnénk, akkor az impulzus teljesen bizonytalanná válna; ha viszont az impulzust mérjük pontosan, akkor a részecske helyzete válik teljesen bizonytalanná. Hogy elképzelésünk legyen a Heisenberg-féle összefüggés korlátjának nagyságáról, tegyük fel, hogy egy elektron helyzetét egy nanométer (10–9 m) pontossággal mérjük; impulzusa ekkor annyira bizonytalanná válna, hogy egy másodperccel később akár 100 kilométer távolságban is lehetne!
Egyes leírásokból azt lehet hinni, hogy ez csupán a mérési folyamatban benne rejlő egyfajta beépített ügyetlenség. Ezek szerint az elektron előbbi esetében a lokalizálási szándék elkerülhetetlenül véletlenszerű „lökést” ad neki, olyan erőset, hogy az elektron valószínűleg elrepül a Heisenberg-elv által jelzett nagyságú sebességgel. Más leírásokban azt olvassuk, hogy a határozatlanság magának a részecskének a tulajdonsága, mozgásában inherens véletlenszerűség van, ami által viselkedése a kvantumszinten megjósolhatatlan. Megint más helyeken azt találjuk, hogy egy kvantumos részecske az valami megfoghatatlan, amelyre maguk a klasszikus hely- és impulzusfogalmak alkalmazhatatlanok. Egyik magyarázattal sem értek egyet. Az első némiképp félrevezető; a második biztosan rossz; a harmadik pedig túlságosan pesszimista.
Mit mond igazából a hullámfüggvény-leírás? Idézzük fel először az impulzusállapot leírását. Ez az a helyzet, ahol az impulzus pontosan meghatározott. A ψ görbe egy dugóhúzó, amely a tengelytől mindvégig azonos távolságban marad. A különböző helyértékek amplitúdóinak abszolútérték-négyzetei ezért egyenlőek. Így ha helymérést végzünk, akkor a részecskét az egyik vagy másik pontban azonos valószínűséggel találjuk meg. A részecske helyzete valóban teljesen bizonytalan! Milyen a helyállapot? A ψ görbe most egy delta-függvény. A részecske pontosan lokalizált – abban a pontban, ahol a delta-függvény kicsúcsosodik –, minden más helyzet amplitúdója zérus. Az impulzusamplitúdókat legjobban az impulzustérbeli leírásból kaphatjuk meg, most a ![]()
görbe a dugóhúzó, ezért most a különböző impulzusamplitúdók abszolútérték-négyzetei egyenlőek. A részecske impulzusát mérve az eredmény most teljesen bizonytalan!
Érdekes megvizsgálni egy közbenső állapotot, amelyben a helyzetek és impulzusok egyaránt csak részben korlátozottak, olyan mértékben, amely megfelel a Heisenberg-összefüggésnek. Egy ilyen eset ψ görbéje és a megfelelő ![]()
görbe (egymás Fourier-transzformáltjai) a 6.14. ábrán látható. Vegyük észre, hogy mindkét görbe tengelytől mért távolsága csak egy kis tartományban jelentős. Nagyon messze a görbék nagyon megközelítik a tengelyt. Ez azt jelenti, hogy az abszolútérték-négyzetek csak egy nagyon korlátozott tartományban jelentős nagyságúak, mind a helyzettérben, mind az impulzustérben. Így a részecsketérben eléggé lokalizált lehet, de bizonyos szórás van; az impulzus hasonlóképpen eléggé meghatározott, így a részecske eléggé határozott sebességgel mozog, és a lehetséges helyzetek szórása nem nő túl nagyra az idő során. Az ilyen kvantumállapot neve hullámcsomag; gyakran ezt veszik a klasszikus részecske legjobb kvantumelméleti közelítésének. Azonban az impulzus- (azaz sebesség-) értékek szórása azzal jár, hogy a hullámcsomag az idő során szétterjed. Minél lokalizáltabb az induláskor, annál gyorsabban fog szétterjedni.
Az U és R fejlesztési eljárások
A hullámcsomag időbeli fejlődésének e leírása mögött hallgatólagosan a Schrödinger-egyenlet húzódik meg, amely megmondja, hogyan változik ténylegesen a hullámfüggvény az időben. Igazából annyit mond, hogy ha ψ-t szétbontjuk impulzusállapotokra („tiszta hangok”), akkor mindegyik összetevő olyan sebességgel mozog, amely c2 osztva a szóban forgó impulzusú klasszikus részecske sebességével. Schrödinger matematikai egyenlete ennél valójában tömörebben van felírva. Egzakt alakját később megszemléljük. Némileg emlékeztet Hamilton vagy Maxwell egyenleteire (mindkettővel szoros kapcsolatban áll), és azokhoz hasonlóan a hullámfüggvény tökéletesen determinisztikus fejlődését adja meg, ha az egy tetszőleges időpontban elő van írva!
ψ-t úgy tekintve, mint ami a világ „valóságát” írja le, nincs semmiféle indeterminizmusunk, amit a kvantumelmélet inherens tulajdonságának feltételeznek – mindaddig, amíg ψ-t a determinisztikus Schrödinger-fejlődés irányítja. Legyen e fejlődési folyamat neve U. Ám amikor a kvantumos jelenségeket a klasszikus szintre felnagyítva „mérést végzünk”, megváltoztatjuk a szabályokat. Nem használjuk U-t, helyette egy teljesen különböző eljárást fogadunk el, R-nek fogom nevezni, ezzel képezzük a kvantumamplitúdók abszolútérték-négyzeteit, hogy megkapjuk a klasszikus valószínűségeket!114 Az R eljárás és csak ez vezet be bizonytalanságokat és valószínűségeket a kvantumelméletbe.
A számoló fizikusok szempontjából az U determinisztikus folyamat látszik a kvantumelmélet döntő fontosságú részének; a filozófusokat mégis jobban érdekli a nemdeterminisztikus R állapotvektor-redukció (vagy ahogy olykor képszerűen nevezik: a hullámfüggvény kollapszusa). Attól függően, hogy R-et egyszerűen csak egy rendszerről elérhető „tudásunkban” bekövetkező változásnak tekintjük, vagy (ahogy magam is) valami „valódinak” vesszük, két teljesen különböző matematikai útra lépünk, másképpen írjuk le egy fizikai rendszer állapotvektorának időbeli változását. U teljesen determinisztikus, míg R valószínűségi törvény; U megőrzi a kvantumelmélet komplex szuperpozícióját, R durván megsérti azt; U folytonos módon működik, R otrombán nem folytonos. A kvantummechanika szabványos eljárásai nem teszik lehetővé, hogy valamilyen módon „levezessük” R-t mint U egy bonyolult példáját. Az U-tól különböző eljárás a kvantumos formalizmus értelmezésének másik „fele”. Az elmélet minden nemdeterminisztikus jellege R-ből származik és nem U-ból. A kvantumelmélet és a megfigyelt jelenségek minden csodálatos egyezéséhez mind U-ra, mind R-re szükség van.
Térjünk vissza ψ hullámfüggvényünkhöz. Tegyük fel, hogy impulzusállapotról van szó. Ez mindaddig békésen megmarad, amíg a részecske nem hat kölcsön valamivel. (Ezt mondja nekünk a Schrödinger-egyenlet.) Ha bármikor úgy határozunk, hogy „megmérjük impulzusát”, mindig ugyanazt a határozott választ kapjuk. Itt nincsenek valószínűségek. A jósolhatóság ugyanolyan nyilvánvaló, mint a klasszikus elméletben. Tegyük azonban fel, valamikor úgy határozunk, hogy megmérjük (a klasszikus szintre felnagyítjuk) a részecske helyét. Ekkor azt találjuk, hogy vannak valószínűségi amplitúdóink, amelyek abszolút értékeit négyzetre kell emelnünk. Ez a pont bővelkedik a valószínűségekben, és teljes a bizonytalanság, milyen eredményt fog hozni a mérés. A bizonytalanság összhangban van a Heisenberg-elvvel.
Tegyük fel másrészt, hogy helyzetállapotú (vagy majdnem ilyen) ψ-vel indulunk. A Schrödinger-egyenlet most azt mondja nekünk, hogy ψ nem marad helyzetállapotban, hanem gyorsan szétterjed. Azt a módot azonban, ahogy szétterjed, az egyenlet teljesen meghatározza. Elvileg találhatnánk olyan kísérleteket, amelyekkel ezt a tényt ellenőrizhetnénk. (Erről többet később.) De ha oktalanul az impulzusát mérjük meg, akkor azt találjuk, hogy mindegyik lehetséges, különböző impulzusérték amplitúdójának az abszolútérték-négyzete egyenlő, és a kísérlet eredménye tökéletesen bizonytalan – ismét összhangban a Heisenberg-elvvel.
Hasonlóképpen, ha hullámcsomag ψ-vel indulunk, annak fejlődését a Schrödinger-egyenlet tökéletesen rögzíti, és elvileg ki lehet gondolni kísérleteket ennek nyomon követésére. De amint különböző módon mérjük a részecskét – mondjuk helyzetét vagy impulzusát –, akkor azt találjuk, hogy bizonytalanságok lépnek be, ismét összhangban a Heisenberg-elvvel, az amplitúdók abszolútérték-négyzetei által megadott valószínűségekkel.
A helyzet kétségtelenül nagyon furcsa és titokzatos. De a kép nem megfoghatatlan képe a világnak. Sok olyan része van, amelyet nagyon világos és pontos törvények szabályoznak. Egyelőre nincs azonban világos szabály arra, mikor kell a valószínűségi R szabályhoz fordulni a determinisztikus U helyett. Mi egy „mérés”? Miért (és mikor) „válnak valószínűségekké” az amplitúdók abszolútérték-négyzetei? Meg lehet-e érteni a „klasszikus szintet” kvantummechanikailag? Ezek mély és rejtélyes kérdések, amelyeket még majd e fejezetben megvizsgálunk.
114 E két fejlődési folyamatot … Neumann János (1955) írta le egy klasszikus művében. Az ő „1-es folyamatát” – „az állapotvektor redukcióját” – neveztem R-nek, 2-es folyamatát – az „unitér fejlődést” (ami lényegében azt jelenti, hogy a valószínűségi amplitúdók a fejlődés során megmaradnak) – U-nak. A kvantumállapotok U fejlődésének vannak más – bár ekvivalens – leírásai is, amelyekben nem használhatjuk a „Schrödinger-egyenlet” kifejezést. A „Heisenberg-képben” például az állapot egyáltalán nem fejlődik, a dinamikai fejlődés a hely/impulzus-koordináták jelentésének folyamatos változására tolódik át. Az eltérések nem fontosak számunkra, lévén az U folyamat különböző leírásai teljesen egyenértékűek.
a „tudásunkban” bekövetkező változás, vagy valami „valódi” …
Részecskék két helyen egyszerre?
Fenti leírásomban a hullámfüggvénynek egy sokkal inkább „realisztikus” szemléletét fogadtam el, mint ami a kvantumfizikusok körében talán szokásos. Arra a nézőpontra helyezkedtem, hogy egy egyedi részecske „objektíven valós” állapotát írja le a hullámfüggvény. Ezt, úgy látszik, sok ember túl nehéz álláspontnak tartja ahhoz, hogy komolyan ragaszkodjék hozzá. Ennek egyik oka az lehet, hogy magában foglalja annak lehetőségét, hogy egyedi részecskék a térben szétterjedjenek, és ne mindig egyetlen pontra koncentrálódjanak. E szétterjedés az impulzusállapotnál a legszélsőségesebb, mert ψ ott egyenletesen oszlik el az egész térben. Ahelyett, hogy a részecskét gondolnák az egész térben szétterjedtnek, az emberek jobban szeretik a helyzetét „teljesen bizonytalannak” tekinteni, így minden, amit erről mondani lehet, az, hogy a részecske egyenlő valószínűséggel lehet bármelyik pontban. Láttuk azonban, hogy a hullámfüggvény nem csupán valószínűségi eloszlást ad a különböző helyzetekre, hanem amplitúdóeloszlást is. Ha ismerjük ezt az amplitúdóeloszlást (azaz a ψ függvényt), akkor – a Schrödinger-egyenletből – ismerjük annak pontos útját, ahogy a részecske állapota egyik pillanatról a következőre fejlődni fog. Szükségünk van a részecske e „szétterjedt” szemléletére, hogy „mozgása” (azaz ψ időbeli fejlődése) meghatározott legyen; és ha elfogadjuk e szemléletet, akkor látjuk, hogy a részecske mozgása valóban pontosan meghatározott. A ψ(x)-re vonatkozó „valószínűségi szemlélet” megfelelő volna, ha helyzetmérést hajtanánk végre a részecskén, és ψ(x)-et azután csak abszolútérték-négyzet formájában használnánk: |(x)|2.
Úgy látszik, ki kell egyeznünk ezzel a részecskeképpel, amely a tér nagy tartományaira szétterjedhet, és amely valószínűleg szétterjedt marad, amíg a következő helymérést el nem végzik. Még amikor egy helyzetállapotban lokalizált is, a következő pillanatban a részecske kezd szétterjedni. Egy impulzusállapot nehezen elfogadhatónak tűnhet mint a részecskelétezés „valóságának” képe, de talán még nehezebb „valóságosnak” elfogadni a kétcsúcsú állapotot, amely akkor jelenik meg, amikor a részecske egy réspáron haladt keresztül (6.15. ábra). A ψ hullámfüggvény alakja a függőleges irányban élesen kicsúcsosodna mindkét rés helyén, lévén összege115 egy ψf hullámfüggvénynek, amelynek a felső résnél van éles csúcsa, és egy ψa-nek, amelynek az alsónál:
Ha a részecske állapotának „valóságát” jeleníti meg, akkor el kell fogadnunk, hogy a részecske valóban két helyen „van” egyszerre! Ebben a szemléletben a részecske tényleg egyszerre haladt át mindkét résen.
Emlékezzünk vissza, mi erre a szokásos ellenvetés: ha mérést végzünk a réseknél, hogy meghatározzuk, melyiken ment a részecske keresztül, mindig azt találjuk, hogy a teljes részecske van az egyik vagy a másik résnél. De ez azért van így, mert helyzetmérést hajtunk végre a részecskén, vagyis ψ most csupán a részecske helyzetére vonatkozó |ψ|2 valószínűségi eloszlással szolgál az abszolútérték-négyzetes eljárással összhangban, és valóban mindig éppen az egyik vagy másik helyen találjuk. Vannak azonban másféle, nem a helyzetet meghatározó mérések, amelyeket végre tudnánk hajtani a réseknél. Ezekhez a kétcsúcsú ψ hullámfüggvényt kellene ismernünk x különböző értékeire, és nem |ψ|2-et. Egy ilyen mérés különbséget tehet az előbbiekben megadott, kétcsúcsú
ψ = ψf + ψa
állapot és más kétcsúcsú állapotok, például
ψ = ψf – ψa,
vagy
ψ = ψf + iψa
között. (Lásd az egyes eseteket a 6.16. ábrán.) Mivel valóban vannak mérések, amelyek megkülönböztetik e változatos lehetőségeket, ezért mindegyik különböző lehetséges „aktuális” módja kell legyen a foton létezésének!
A réseknek nem kell közel lenniük egymáshoz, hogy egy foton keresztül tudjon menni „mindkettőn egyszerre”. Hogy lássuk, hogy egy kvantumos részecske igenis lehet „két helyen egyszerre”, függetlenül attól, mekkora távolság van ezek között, tekintsünk egy, a kétrés-kísérlettől kissé különböző elrendezést. Mint előbb, van egy monokromatikus fényt – egyszerre egy fotont – kibocsátó lámpánk; de a fényt most nem egy réspáron bocsátjuk keresztül, hanem a nyaláb irányával 45°-os szöget bezáró, félig ezüstözött tükörrel visszaverjük. (A félig ezüstözött tükör a ráeső fénynek pontosan a felét veri vissza, a másik felét átengedi.) A tükörrel való találkozás után a foton hullámfüggvénye két részre hasad, az egyik rész oldalra visszaverődik, a másik folytatja útját a foton eredeti irányában. A hullámfüggvény megint kétcsúcsú, mint a réspárból felbukkanó foton esetében, de a két csúcs most sokkal messzebb van egymástól, az egyik a visszaverődő, a másik az átmenő fotont írja le (lásd 6.17. ábra). Mi több, ahogy az idő halad, a csúcsok közötti távolság egyre nagyobb és nagyobb lesz, minden határon túlnő. Képzeljük el, hogy a hullámfüggvény két része kiszökik a térbe, és várunk egy egész évig. A foton hullámfüggvényének két csúcsa akkor már egy fényév távolságra lesz. A foton valahogy egyszerre két helyen van, amelyek több mint egy fényévnyire vannak egymástól!
Van-e okunk arra, hogy komolyan vegyük ezt a képet? Nem tekinthetjük-e a fotont úgy, hogy 50% valószínűséggel az egyik helyen, 50% valószínűséggel a másikon van? Nem, ezt nem tehetjük! Függetlenül attól, milyen messze ment el, mindig fennáll annak a lehetősége, hogy a nyaláb két része visszaverődve újra találkozzék és interferenciajelenségeket hozzon létre, amely a két lehetőség valószínűségi súlyozása esetén nem következhetne be. Tegyük fel, hogy a nyaláb mindkét része teljesen ezüstözött tükörrel találkozik, amelyek olyan szögben vannak beállítva, hogy újra összehozzák a nyalábokat, a találkozási pontban pedig egy másik, félig ezüstözött tükör van éppen olyan szögben, mint az első. A nyalábok további útjába egy-egy fotocellát helyeztünk el (lásd 6.18. ábra). Mit fogunk észlelni? Ha csupán az volna a helyzet, hogy a foton 50% valószínűséggel az egyik, 50% valószínűséggel a másik utat követi, akkor azt találnánk, hogy az egyik és másik detektor 50-50% valószínűséggel jelzi a fotont. Azonban nem ez történik. Ha a két lehetséges út pontosan egyenlő hosszúságú, akkor a foton 100% valószínűséggel éri el az eredeti mozgás irányában elhelyezett A detektort, és 0 valószínűséggel a másik, B detektort – a foton biztosan az A detektort szólaltatja meg! (Beláthatjuk ezt, használva a korábbi dugóhúzó-leírást, ugyanúgy, mint a kétrés-kísérletnél.)
Ilyen kísérletet természetesen soha nem hajtottak végre fényév nagyságrendű úthosszúságokkal, de az elmondott eredményt nem vonják komolyan kétségbe (a hagyományos kvantumfizikusok!). Elvégeztek ilyen jellegű kísérleteket sokméteres úthosszakkal, és az eredmények valóban teljesen megegyeznek a kvantummechanikai jóslatokkal (vö. Wheeler 1983). Mit mond ez nekünk a foton létezéséről a félig visszaverő tükrökkel való találkozásai között? Elkerülhetetlennek látszik, hogy a fotonnak, valamilyen értelemben, ténylegesen utaznia kell mindkét úton egyszerre! Mert ha egy elnyelő ernyőt helyezünk a két út egyikére, akkor utána egyenlő valószínűséggel éri el A-t vagy B-t; de ha mindkét út nyitva van (és egyenlő hosszúságú), akkor csak A-t tudja elérni. Az egyik út lezárása lehetővé teszi, hogy a foton B-be jusson! Ha mindkét út nyitva van, akkor a foton valahogy „tudja”, hogy nem mehet B-be, így ténylegesen ki kell tapogatnia mindkét utat.
Niels Bohr nézete, hogy a foton létezésének a mérések pillanatai között nem lehet objektív „értelmet” tulajdonítani, számomra nagyon-nagyon pesszimistának látszik a foton állapotának valóságát illetően. A kvantummechanika egy hullámfüggvényt ad nekünk, hogy leírjuk a foton helyzetének „valóságát”, és a két, félig ezüstözött tükör között a hullámfüggvény éppen egy kétcsúcsú állapot, amelyben a két csúcs távolsága olykor nagyon jelentós.
Megjegyezzük még, hogy a „két meghatározott helyen van egyszerre” nem teljes leírása a foton állapotának: meg kell tudnunk különböztetni a ψf + ψa állapotot mondjuk ψf – ψa állapottól (vagy mondjuk a ψf + iψa-től), ahol ψf és ψa a foton helyzeteire vonatkozik az egyes utakon. Ez a megkülönböztetés az, ami meghatározza, hogy a foton a második félig ezüstözött tükör után biztosan A-ba vagy biztosan B-be jut-e (vagy mindkettőt valamilyen közbenső valószínűséggel éri el).
A kvantumos valóság e rejtélyes tulajdonsága – nevezetesen, hogy komolyan kell vennünk, hogy egy részecske változatos (különböző!) módokon „lehet két helyen egyszerre” – abból a tényből származik, hogy meg kell engednünk a kvantumállapotok komplex számokkal súlyozott összeadását, ami újabb kvantumállapotokra vezet. Az állapotok effajta szuperpozíciója a kvantummechanika általános – és fontos – tulajdonsága, neve kvantumos lineáris szuperpozíció. Ez teszi lehetővé, hogy helyzetállapotokból impulzusállapotokat építsünk fel, vagy impulzusállapotokból helyzetállapotokat. Ezekben az esetekben a lineáris szuperpozícióban végtelen sok különböző állapot szerepel, minden különböző helyzetállapot vagy minden különböző impulzusállapot. De amint láttuk, a kvantumos lineáris szuperpozíció eléggé rejtélyes akkor is, amikor csak egy állapotpárra vonatkozik. A szabály az, hogy tetszőleges két állapot, függetlenül attól, mennyire különbözők lehetnek, tetszőleges komplex lineáris kombinációban együtt élhet. Valójában minden egyedi részecskékből álló fizikai objektumnak képesnek kellene lennie arra, hogy ilyen térbelileg nagyon elkülönülő állapotok szuperpozíciójában létezzen, és így „egyszerre legyen két helyen”! A kvantummechanika formalizmusa ebben a vonatkozásban nem tesz különbséget az egyetlen részecske és a sok részecskéből álló bonyolult rendszerek között. Miért nem látunk akkor makroszkopikus testeket, mondjuk krikettlabdákat, sőt embereket két tökéletesen különböző helyen egyszerre? Ez igen mély kérdés, és a mai kvantumelmélet nem nyújt igazán kielégítő választ. Egy olyan szilárd objektumnál, mint egy krikettlabda, a rendszert a „klasszikus szinten” lévőnek kell tekintenünk – vagy, a szokásosabb megfogalmazásban, „megfigyelést” vagy „mérést” végzünk a krikettlabdán –, és akkor a komplex valószínűségi amplitúdók, amelyek lineáris szuperpozíciónkat súlyozzák, abszolútérték-négyzeteikkel kell megjelenjenek, mint amik leírják a tényleges lehetőségek valószínűségeit. Így azonban igazából csak megkerüljük a vitatott kérdést, miért szabad a kvantumos szabályokban ezen a módon áttérni U-ról R-re! Erre a kérdésre később visszatérek.
Átmenet egyikből a másikba. Második folytatás.
6. Kvantumvarázslatok, kvantumtitkok
Hilbert-tér
Emlékezzünk vissza, hogy a fázistér fogalmát az 5. fejezetben a klasszikus rendszerek leírására vezettük be. A fázistér egyetlen pontját használtuk egy teljes fizikai rendszer (klasszikus) állapotának ábrázolására. A kvantumelméletben az ezzel analóg fogalom a Hilbert-tér fogalma.116 A Hilbert-tér egy pontja most egy egész rendszer egy kvantumállapotát ábrázolja. Egy pillantást kell majd vetnünk a Hilbert-tér matematikai szerkezetére. Remélem, az Olvasót ez nem fogja megijeszteni. Abban, amit el kell mondanom, nincs semmi matematikailag nagyon bonyolult, bár egyes dolgok szokatlanok lehetnek.
Egy Hilbert-tér legalapvetőbb tulajdonsága az, hogy vektortér – valójában komplex vektortér. Ez azt jelenti, hogy összeadva a tér két elemét, egy másik ilyen elemet kapunk; és az összeadást komplexszám-súlyozással is végrehajthatjuk. Ezekre szükségünk van, mert éppen ezek az előbb említett kvantumos lineáris szuperpozíció műveletei, nevezetesen amelyek megadják ψf + ψa-t, ψf – ψa-t, ψf + iψa-t stb. az előző fotonra. A „komplex vektortér” kifejezésen lényegében semmi mást nem értünk, mint azt, hogy ilyen súlyozott összegek képezhetők.
Kényelmes lesz, ha elfogadunk egy (lényegében Diractól származó) jelölést, amely szerint a Hilbert-tér elemeit – az ún. állapotvektorokat – egy ∣〉 alakú zárójelben álló szimbólumma
l jelöljük, mint például ∣ψ〉, ∣χ〉, ∣φ〉, ∣1〉, ∣2〉, ∣3〉, ∣n〉, ∣1〉, ∣↑〉, ∣↓〉, ∣→〉, ∣↗〉 stb
. Ezek a szimbólumok most tehát kvantumállapotokat jelölnek. Két állapotvektor összeadását így írjuk:
∣ψ〉 + ∣χ〉,
és a w és z komplex számokkal súlyozva:
w∣ψ〉 + z∣χ〉
(ahol w∣ψ〉 w ∙ ∣ψ〉-t jelenti stb.). A fenti ψf + ψa, ψf – ψa, ψf + iψf kombinációkat most rendre úgy írjuk, hogy |ψf〉 + |ψa〉, |ψf〉 – |ψa〉, |ψf〉 + i|ψa〉. Egyetlen |ψ〉 állapotot is megszorozhatunk egy w komplex számmal:
w|ψ〉.
(Ez valójában az előző speciális esete, amikor z = 0.)117
Emlékezzünk rá, hogy megengedtünk komplex számokkal súlyozott kombinációkat, ahol w és z nem a tényleges valószínűségi amplitúdók, csupán arányosak azokkal. Ezek szerint azt a szabályt fogadjuk el, hogy egy teljes állapotvektort megszorozhatunk egy nemzérus komplex számmal, és ekkor a fizikai állapot nem változik. (w és z értékei ilyenkor megváltoznak, de a w : z arány nem.) A
|ψ〉, 2 |ψ〉, – |ψ〉, i |ψ〉,
vektorok ugyanazt a fizikai állapotot ábrázolják – mint egy tetszőleges z|ψ〉 is, ahol z ≠ 0. A Hilbert-tér egyetlen eleme, amelynek nem felel meg fizikai állapot, a 0 zérus vektor (a Hilbert-tér kezdőpontja).
...
Vektormennyiségre példa egy részecskére ható erő. Más példák a klasszikus sebességek, gyorsulások, impulzusok. Vektorok az impulzus négyesvektorok is, amelyekről az előző fejezet végén volt szó. Azok nem két vagy három, hanem négy dimenzióban vektorok. A Hilbert-térben azonban még sokkal magasabb (gyakran végtelen, de ez nem lesz lényeges) dimenziós vektorokra van szükségünk. Emlékezzünk rá, hogy a klasszikus fázistérben is használtunk nyilakat a vektorok ábrázolására – azok biztosan nagyon nagy dimenziószámúak lehetnek. A fázistér „dimenziói” nem közönséges térdimenziókat képviselnek, ugyanúgy a Hilbert-tér „dimenziói” sem. Ehelyett a Hilbert-térbeli minden dimenzió egy kvantumrendszer különböző független fizikai állapotai egyikének felel meg.
A |ψ〉 és z|ψ〉 közötti ekvivalencia miatt egy fizikai állapotnak ténylegesen az O kezdőponton átmenő egyenes vagy sugár felel meg a Hilbert-térben (ez ábrázolja egy vektor minden számszorosát), nemcsak egy vektor az egyenesen. A sugár egy speciális |ψ〉 állapotvektor minden lehetséges többszörösét tartalmazza. (Tartsuk fejben, hogy komplex szorzókról van szó, így a vonal ténylegesen egy komplex vonal, de most jobb ezzel nem törődni!) (Lásd 6.20. ábra.) Hamarosan elegáns képünk lesz a sugaraknak e teréről a kétdimenziós Hilbert-tér esetében. A másik szélsőséges eset az, amikor a Hilbert-tér végtelen dimenziós. Ilyennel kell dolgoznunk még abban az egyszerű esetben is, amikor egyetlen részecske helyzetét vizsgáljuk. Ekkor a részecske által felvehető minden lehetséges helyzet egy teljes dimenziót tesz ki! Mindegyik részecskehelyzet egy egész „koordinátatengelyt” definiál a Hilbert-térben, így a végtelen sok különböző helyzet végtelen sok különböző, független irányt (vagy „dimenziót”) jelent. Ugyanebben a Hilbert-térben ábrázoljuk az impulzusállapotokat is. Ezek helyzetállapotok kombinációiként fejezhetők ki, ezért minden impulzusállapotnak megfelel egy „átlósan” futó tengely, amely valamilyen szögben dől a helyzettér tengelyeihez képest. Az összes impulzusállapot halmaza egy új tengelyhalmazt ad, és a helyzettér tengelyeiről az impulzustér tengelyeire való áttérés forgatást jelent a Hilbert-térben.
Nem kell arra törekednünk, hogy ezt pontosan szemléltessük. Ésszerűtlen dolog volna! Sokat segítenek azonban bizonyos, a közönséges euklideszi geometriából átvett gondolatok. Speciálisan a szóban forgó tengelyeket (akár a helyzettérbelieket, akár az impulzustérbelieket) egymásra mind merőlegeseknek gondoljuk, azaz kölcsönösen „derékszögűeknek”. A sugarak közötti „merőlegesség” a kvantummechanika fontos fogalma: a merőleges sugarak olyan állapotokat ábrázolnak, amelyek függetlenek egymástól. Egy részecske különböző lehetséges helyzetállapotai mind merőlegesek egymásra, mint ahogy a különböző lehetséges impulzusállapotok is. Nem merőlegesek viszont a helyzetállapotok az impulzusállapotokra. A helyzetet a 6.21. ábra mutatja, nagyon vázlatosan.
Mérések
A mérésre (vagy megfigyelésre) vonatkozó általános R szabály megköveteli, hogy egy kvantumos rendszer különböző oldalai, amelyek egyidejűleg nagyíthatók fel a klasszikus szintre – és amelyek között a rendszernek választania kell – mindig ortogonálisak legyenek. Teljes mérésnél a lehetőségek kiválasztott halmaza merőleges bázisvektorok egy halmazát képezi, ami azt jelenti, hogy segítségükkel a Hilbert-tér minden vektora lineáris módon (egyértelműen) kifejezhető. Helyzetmérésnél – egyetlen részecskéből álló rendszer esetén – a bázisvektorokat az előbbiekben vizsgált helyzettengelyek definiálják. Az impulzusra az impulzustengelyek definiálnak egy különböző halmazt, és másfajta teljes mérésnél megint más a halmaz. A mérés után a rendszer állapota beugrik a mérés által meghatározott halmaz egyik tengelyére – választását csak a valószínűségek szabályozzák. Nincs semmiféle dinamikai törvény, amely megmondaná, melyik tengelyt választja a Természet. Választása véletlenszerű, a valószínűségértékek a valószínűségi amplitúdók abszolútérték-négyzetei.
Tegyük fel, hogy egy rendszeren, amelynek állapota |ψ〉, teljes mérést végzünk, az erre vonatkozó bázis legyen
|0〉, |1〉, |2〉, |3〉, … .
Mivel ezek teljes rendszert alkotnak, ezért segítségükkel tetszőleges állapotvektor, speciálisan |ψ〉 is, lineáris formában kifejezhető:118
|ψ〉 = z0|0〉 + z1|1〉 + z2|2〉 + z3|3〉 + … .
A z0, z1, z2, … összetevők a |ψ〉 vektor |0〉, |1〉, |2〉, … tengelyekre eső merőleges vetületeinek nagyságait mérik (lásd 6.22. ábra).
Szeretnénk, ha a z0, z1, z2, … komplex számokat úgy értelmezhetnénk, mint a kívánt valószínűségi amplitúdókat, ezek abszolútérték-négyzetei adják annak valószínűségeit, hogy a rendszer a mérés után a megfelelő |0〉, |1〉, |2〉, … állapotokban található. Azonban ez nem egészen lesz így, mert nem rögzítettük a bázisvektorok „nagyságát”. Elő kell írnunk, hogy azok valamilyen értelemben egységvektorok (azaz „hosszúságuk” egységnyi), és így, a matematikai kifejezést használva, ortonormált bázist alkotnak (páronként merőlegesek, más néven ortogonálisak, továbbá egységvektorok).119 Ha |ψ〉 is egységvektorként normált, akkor a keresett amplitúdók valóban a |ψ〉 z0, z1, z2, … összetevői lesznek, a keresett valószínűségek pedig rendre |z0|2, |z1|2, |z2|2, … Ha |ψ〉 nem egységvektor, akkor ezek a számok arányosak lesznek a keresett amplitúdókkal, illetve valószínűségekkel. A tényleges amplitúdók:
a tényleges valószínűségek:
lesznek, ahol |ψ| a |ψ〉 állapotvektor „hossza”. Ez a „hosszúság” minden állapotvektorra meghatározott pozitív szám (a 0 hossza zérus), és |ψ| = 1, ha |ψ〉 egységvektor.
A méréseknek nagyon idealizált fajtája a teljes mérés. Egy részecske helyzetének teljes mérése például megkövetelné, hogy a részecskét végtelen pontossággal tudjuk lokalizálni akárhol a világegyetemben! Elemibb típusú mérés az, amelynél csak igen-nem típusú kérdést teszünk fel, mint például: „A részecske egy vonaltól bal vagy jobbra helyezkedik-e el?”– vagy: „Belül van-e a részecske impulzusa egy bizonyos tartományon?” – stb. Az igen-nem mérések valójában a legalapvetőbb mérések. (Például egy részecske helyzetét vagy impulzusát csak igen-nem méréseket használva annyira be lehet határolni, amennyire csak akarjuk.) Tegyük fel, hogy egy igen-nem mérés eredménye IGEN. Ekkor az állapovektornak a Hilbert-tér „IGEN” tartományában kell lennie, amelyet I-nek fogok nevezni. Ha viszont a mérés eredménye NEM, akkor az állapotvektor a Hilbert-tér „NEM” tartományában van, jele N. Az I és N tartományok teljesen ortogonálisak egymásra abban az értelemben, hogy bármely I-hez tartozó állapotvektornak ortogonálisnak kell lennie minden N-hez tartozó állapotvektorra (és viszont). Továbbmenve: tetszőleges |ψ〉 állapotvektor (egyértelműen) kifejezhető egy I-be és egy N-be tartozó vektor összegeként. Matematikai kifejezéssel azt mondjuk, hogy I és N egymás ortogonális komplementerei. Így |ψ〉 egyértelműen felírható a következő alakban:
|ψ〉 = |ψI〉 + |ψN〉,
ahol |ψI〉 I-hez, |ψN〉 N-hez tartozik. |ψI〉 a |ψ〉 állapot merőleges vetülete I-re, |ψN〉 a |ψ〉 merőleges vetülete N-re (lásd 6.23. ábra).
A mérésnél a |ψ〉 állapot ugrik – és vagy |ψI〉-vé, vagy |ψN〉-né válik (arányos lesz velük). Ha az eredmény IGEN, akkor |ψI〉-be ugrik, ha NEM, akkor |ψN〉-be. Ha |ψ〉 normált, akkor e két esemény megfelelő valószínűségei a vetített állapotok
|ψI|2, |ψN|2
négyzetes hosszai. Ha |ψ〉 nem normált, akkor mindkét kifejezést el kell osztanunk |ψ|2-tel. (A |ψ|2 = |ψI|2 + |ψN|2 „Pitagorasz-tétel” biztosítja, hogy e valószínűségek összege egységnyi, ahogy annak lennie kell!) Jegyezzük meg: annak valószínűségét, hogy |ψ〉 a |ψI〉-be ugrik át, az az arány adja, amely szerint négyzetes hossza e vetítés során csökken.
Egy végső megjegyzést még a kvantumrendszereken végrehajtható „mérési aktusokról”. Az elmélet elveinek egy velejárója, hogy tetszőleges állapotra – mondjuk a ∣χ〉-re – nézve elvileg végrehajtható egy igen-nem mérés,120 amelynek eredménye IGEN, ha a mért állapot megegyezik (arányos) ∣χ〉-vel, NEM, ha ortogonális ∣χ〉-re. Így az I tartomány a tetszőlegesen választott ∣χ〉 állapot összes számszorosát tartalmazza. Ennek az a határozott következménye látszik, hogy az állapotvektoroknak objektíven valóságosaknak kell lenniük. Akármi is egy fizikai rendszer állapota – nevezzük ezt az állapotot ∣χ〉-nek –, van egy elvileg végrehajtható mérés, amelynek szempontjából ∣χ〉 az egyetlen állapot (arányossági tényező erejéig), amelyben a mérés eredménye IGEN, és ebben biztosan az. Egyes ∣χ〉 állapotokra ez a mérés rendkívül nehezen végrehajtható lehet – esetleg gyakorlatilag „lehetetlen” –, de annak a ténynek, hogy az elmélet szerint elvileg végezhető ilyen mérés, meglepő következményeivel fogunk találkozni később e fejezetben.
A spin és az állapotok Riemann-gömbje
A kvantummechanikában „spin”-nek nevezett mennyiséget olykor minden fizikai mennyiség közül a leginkább „kvantummechanikainak” nevezik, ezért bölcs dolog lesz, ha komoly figyelmet fordítunk reá. Mi a spin? Lényegében egy részecske forgásának mértéke. Maga a „spin” kifejezés a labda pörgéséhez hasonló valamit sugall. Emlékezzünk vissza az impulzusmomentumra, amely az energiához és impulzushoz hasonlóan megmaradó mennyiség (lásd 5. fejezet). Egy test impulzusmomentuma mindaddig megmarad, amíg a súrlódási vagy más erő meg nem zavarja. Valójában ilyen a kvantummechanikai spin is, de most bennünket egyetlen részecske „pörgése” érdekel, és nem az egyedi részecskék miriádjainak közös tömegközéppontjuk körüli keringő mozgása (ez a labda pörgése). Figyelemre méltó fizikai tény, hogy a természetben található legtöbb részecske ténylegesen „pörög” ebben az értelemben, mindegyik a saját nagyon specifikus mértéke szerint.121 Látni fogjuk azonban, hogy egy kvantummechanikai részecske spinjének nagyon sajátos tulajdonságai vannak, amelyeket a pörgő labdákkal és hasonló dolgokkal szerzett tapasztalataink alapján egyáltalán nem várnánk.
Elsősorban egy részecske spinjének nagysága mindig ugyanaz, az adott típusú részecskére jellemző állandó. Csak a spin tengelyének iránya változhat (elég furcsa módon, mint látni fogjuk). Ez éles ellentétben áll a labda esetével, amely tetszőleges mértékben pöröghet, s a perdület nagysága attól függ, hogyan pörgetjük meg! Elektron, proton vagy neutron esetében a spin nagysága mindig ħ/2, azaz fele a legkisebb pozitív értéknek, amelyet Bohr az atomok kvantált impulzusmomentumára eredetileg megengedett. (Emlékeztetőül: ezek az értékek 0, ħ, 2ħ, 3ħ, … voltak.) Most a ħ alapegység felét írjuk elő – bizonyos értelemben a ħ/2 a még alapvetőbb egység. Ilyen nagyságú impulzusmomentum nem volna megengedett egy olyan keringő részecskékből álló objektum esetében, amelyek önmagukban nem pörögnek; csak azért jöhet létre, mert a spin magának a részecskének belső tulajdonsága (azaz nem „részeinek” egy középpont körüli keringő mozgásából származik).
Azokat a részecskéket, amelyek spinje ħ/2 páratlan számú többszöröse (tehát ħ/2, 3ħ/2, 5ħ/2 stb.), fermionoknak nevezzük, ezek kvantummechanikai leírásában van egy furcsaság: a teljes, 360°-os forgatás az állapotvektort nem önmagába, hanem önmaga mínusz egyszeresébe viszi át! A Természet sok részecskéje fermion, ezekről, furcsaságaikról – amelyek létezésünk szempontjából annyira életbevágóak – később többet fogunk megtudni. A többi részecskét, amelyek spinje ħ/2 páros számú, azaz ħ egész számú többszöröse (nevezetesen ħ, 2ħ, 3ħ, …), bozonoknak nevezzük. Egy bozon állapotvektorát a 360°-os forgatás önmagába, nem pedig a negatívjába viszi át.
Tekintsünk egy feles spinű, tehát ħ/2 spinértékű részecskét. A határozottság kedvéért úgy fogok róla beszélni, mint elektronról, de ugyanúgy lehetne proton vagy neutron, sőt megfelelő fajta atom is. (Egy „részecskének” lehetnek egyedi alkotórészei mindaddig, amíg kvantummechanikailag jól meghatározott teljes impulzusmomentummal rendelkező, egyetlen egészként kezelhető.) Az elektront nyugalomban lévőnek vesszük, és csak spinállapotát vizsgáljuk. A kvantummechanikai állapottér (Hilbert-tér) most kétdimenziós, ezért két állapotból álló bázist kell választanunk. Ezek jelölésére most a |↑〉 és |↓〉 szimbólumokat használom: |↑〉 azt jelzi, hogy a spin a felfelé mutató függőleges irányhoz, |↓〉 azt, hogy a lefelé mutatóhoz képest jobbkezes (6.24. ábra). A |↑〉 és |↓〉 állapotok egymásra ortogonálisak, és mindkettőt normáltnak vesszük (|↑〉2 = |↓〉2 = 1). Az elektron bármely lehetséges spinállapota a két ortonormált állapot, |↑〉 és |↓〉, azaz a fel és le lineáris szuperpozíciója.
Na már most, a „fel” és „le” irányokban nincsen semmi speciális. Ugyanúgy választhattunk volna tetszőleges más irányt a spin leírására (amelyhez képest jobbkezes), mondjuk a jobb |→〉 és bal |←〉 állapotokat. Ekkor (alkalmas komplex szorzótényezőkkel)122
|→〉 = |↑〉 + |↓〉 | |←〉 = |↑〉 – |→〉 |
Ez új képet nyújt számunkra: az elektron spinjének bármelyik állapota két ortogonális állapot, |→〉 és |←〉, azaz jobb és bal lineáris szuperpozíciója. Választhatunk egy teljesen tetszőleges irányt, mondjuk a |↗〉 állapotvektorral megadottat. Ez megint komplex lineáris kombinációja a |↑〉 és |↓〉 állapotoknak,
|↗〉 = w|↑〉 + z|↓〉,
és minden spinállapot lineáris szuperpozíciója ennek és a |↖〉 ortogonális állapotnak, amelyik |↗〉-val ellentétes irányba mutat.123 (Jegyezzük meg, hogy az „ortogonális” fogalom a Hilbert-térben nem jelent „derékszögűt” a közönséges térben. A Hilbert-tér ortogonális vektorai most a tér ellentétes irányainak felelnek meg, és nem derékszöget bezáróknak.)
Mi a geometriai kapcsolat a |↗〉 által meghatározott térbeli irány és a két komplex szám, w és z között? Mivel a |↗〉 fizikai állapotot egy nem zérus komplex számmal való szorzás nem befolyásolja, ezért csak z és w arányának van jelentése. Legyen ez az arány
q = z/w.
q is valamilyen komplex szám, most a „q = ∞” értéket is megengedjük, hogy megbirkózhassunk a w = 0 esettel is, tehát azzal, amikor a spin iránya függőlegesen lefelé mutat. Ha q ≠ ∞, akkor q-t az Argand-sík egy pontjaként ábrázolhatjuk, ahogy azt a 2. fejezetben tettük. Képzeljük ezt az Argand-síkot a térben vízszintesnek, a valós tengely mutasson „jobbra” (azaz a |→〉 spinállapot irányába). Képzeljünk el egy egységsugarú gömböt, amelynek középpontja az Argand-sík kezdőpontjában van; ekkor az 1, i, –1, –i pontok mind a gömb egyenlítőjére esnek. A déli sarkpontot jelöljük ∞-nel, és vetítsünk ebből a pontból úgy, hogy a teljes Argand-sík leképeződjék a gömbre. Így a sík minden q pontjának egyértelműen megfelel a gömb egy q pontja, amelyet úgy kapunk, hogy a két pontot összekötjük a déli sarkponttal (6.25. ábra). A megfeleltetés neve sztereografikus vetítés, és sok szép geometriai tulajdonsága van (megőrzi például a szögeket, kört körbe visz át). A vetítés módot ad arra, hogy a gömb pontjait komplex számokkal és a ∞-nel felcímkézzük, ezek lesznek a lehetséges q komplex arányok. Az ilyen speciális módon megjelölt gömböt Riemann-gömbnek nevezzük. A Riemann-gömb jelentősége az elektron spinállapotaira nézve az, hogy a |↗〉 = w|↑〉 + z|↓〉 kombinációval megadott spin irányát megkaphatjuk, ha a középpontból a Riemann-gömb q = z/w jelzésű pontjába nyilat rajzolunk. Megjegyezzük, hogy az északi pólus a |↑〉 állapotnak felel meg, amelyre z = 0, azaz q = 0, a déli pólus pedig a |↓〉 állapotnak, amelyre w = 0, azaz q = ∞. A jobb szélső a q = 1 pont, amely a |→〉 = |↑〉 + |↓〉 állapotot, a bal szélső a q = –1 pont, amely a |←〉 = |↑〉 – |↓〉 állapotot adja. A gömb hátsó részén a legtávolabbi a q = i pont, amely a |↑〉 + i|↓〉 állapotnak felel meg, ebben a spin a lapba befelé mutat, a hozzánk legközelebbi a q = –i pont, amely a |↑〉 – i|↓〉 állapotnak felel meg, ebben a spin egyenesen felénk mutat. A q-val jelölt pont általánosan a |↑〉 + i|↓〉 állapotnak felel meg.
Hogyan kapcsolódik mindez az elektron spinjén elvégezhető mérésekhez?124 Válasszunk ki egy irányt a térben; jelöljük ezt α-val! Ha megmérjük az elektron spinjét ebben az irányban, akkor az IGEN válasz azt mondja, hogy az elektron (most) valóban az α irányban pörög (jobbkezesen), míg a NEM válasz azt, hogy az α-val ellentétes irányban.
Tegyük fel, hogy a válasz IGEN; jelöljük ezt az állapotot |α〉-val. Ha pontosan ugyanabban az α irányban egyszerűen megismételjük a mérést, akkor a válasznak újra IGEN-nek kell lennie 100% valószínűséggel. De ha a második mérésre az irányt egy új β irányra változtatjuk, akkor azt találjuk, hogy az IGEN válasz valószínűsége valamivel kisebb, ekkor az állapot |β〉-ba ugrik, és van esély arra, hogy a második mérésre adott válasz NEM lesz, amikor az állapot a β-val ellentétes irányúba ugrik be. Hogyan számítsuk ki ezt a valószínűséget? A választ az előző szakasz végén adott előírások tartalmazzák. Az IGEN valószínűsége a második mérésnél
Látjuk ebből, hogy ha a második mérést az elsővel derékszöget bezáró irányban végezzük, akkor mindkét valószínűség 50% (cos90° = 0): a második mérés eredménye teljesen véletlenszerű! Ha a két mérés iránya hegyesszöget zár be, akkor az IGEN válasz valószínűbb, mint a NEM. Ha tompaszöget, akkor a NEM valószínűbb, mint az IGEN. Abban a szélsőséges esetben, amikor) ellentétes α-val, az IGEN valószínűsége 0-vá, a NEM-é 100%-ká válik; azaz a második mérés eredménye biztosan az első megfordítottja. (A spinről többet lásd Feynman és mások 1965.)
A Riemann-gömb alapvető (de nem mindig felismert) szerepet játszik tetszőleges kétállapotú kvantumrendszernél, leírja (arányossági tényező erejéig) a lehetséges kvantumállapotok elrendeződését. Geometriai szerepe különösen nyilvánvaló a feles spinű részecskénél, mert a gömb pontjai a spintengely lehetséges térbeli irányainak felelnek meg. Sok más helyzetben nehezebb látni a Riemann-gömb szerepét. Tekintsünk egy fotont, amely éppen átjutott egy réspáron, vagy visszaverődött egy félig ezüstözött tükörről. A foton állapota két állapot, a két egészen elkülönülő helyzetet leíró |ψf〉 és |ψa〉 valamilyen lineáris kombinációja, például |ψf〉 + |ψa〉, |ψf〉 – |ψa〉 vagy |ψf〉 + i|ψa〉. A Riemann-gömb leírja a fizikailag különböző lehetőségek elrendezését, de most csak absztrakt módon. A |ψf〉 állapotot az északi („felső”), a |ψa〉-t a déli („alsó”) pólus ábrázolja. A |ψf〉 + |ψa〉, |ψf〉 – |ψa〉 és |ψf〉 + i|ψa〉 állapotokat az egyenlítő különböző pontjai ábrázolják, és általánosan a w|ψf〉 + z|ψa〉 állapotot a q = z/w-vel adott pont. Sok esetben, mint ebben is, a lehetőségek „Riemann-gömb értékei” meglehetősen rejtettek, nincs világos kapcsolatuk a térbeli geometriával.
121 Az egy részecskét tartalmazó kvantumrendszerről adott korábbi leírásom egyszerűsített volt, mert elhagytam a spint, feltételeztem, hogy az állapot leírható egyedül a helyzet függvényeként. Ténylegesen vannak olyan részecskék – skalár részecskéknek hívják ezeket, példa rájuk a pionoknak (π-mezonoknak, vö. 290. o.) nevezett magrészecskék vagy bizonyos atomok –, amelyek spinje zérus. Ezekre a részecskékre (de csak ezekre) a korábbi leírás megfelelő.
123 |↙〉 = z|↑〉 – |↓〉, ahol z és w z és w komplex konjugáltjai. (Lásd a 119. jegyzetet.)
124 Van egy szabványos kísérleti eszköz, a Stern–Gerlach-berendezés, amely használható az atomok spinjének mérésére. Az atomokat egy nyalábban gyűjtik össze, amely áthalad egy erősen inhomogén mágneses mezőn, a mező inhomogenitásának iránya szolgáltatja a spinmérés irányát. A nyaláb (feles spinű atomnál) két részre hasad (magasabb spinű esetén kettőnél több részre), az egyikben azok az atomok vannak, amelyek a spinmérésre IGEN-nel, a másikban azok, amelyek NEM-mel válaszoltak. Technikai okok miatt, amelyek a mi szempontjainkból lényegtelenek, ez a berendezés az elektron spinjének mérésére sajnos nem használható, arra közvetettebb eljárást kell alkalmazni (lásd Mott és Massey 1965). Ezért és egyéb okok miatt jobbnak látom nem részletezni, hogyan mérik a valóságban az elektron spinjét.
125 A vállalkozó szellemű Olvasó ellenőrizheti a szövegben megadott geometriát. Ez akkor a legkönnyebb, ha úgy állítjuk be Riemann-gömbünket, hogy az α irány mutat „felfelé”, a β irány a „fel” és „jobbra” által kifeszített síkban fekszik, azaz q = tg(θ/2)-vel adott a Riemann-gömbön, és ekkor a 〈χ∣ψ〉〈ψ∣χ〉/〈χ∣χ〉〈ψ∣ψ〉 előírást használjuk a ∣ψ〉-ből ∣χ〉-be való ugrás valószínűségére. Lásd 119. jegyzet.
A kvantumállapotok objektivitása és mérhetősége
Annak ellenére, hogy egy kísérlet eredményére általában csak valószínűségeink vannak, egy kvantummechanikai állapotban látszik valami objektív tartalom. Gyakran állítják, hogy az állapotvektor csupán kényelmes leírása egy fizikai rendszerre vonatkozó „tudásunknak” – vagy esetleg hogy az állapotvektor valójában nem ír le egyetlen rendszert, csak valószínűségi információt nyújt egy nagyszámú, hasonlóan elkészített rendszerből álló „sokaságról”. Ezek a vélemények szerintem ésszerűtlenül félénkek azzal kapcsolatban, amit a kvantummechanikának mondania kell nekünk a fizikai világ „valóságosságáról”.
Az állapotvektorok „fizikai valóságára” vonatkozó óvatosság vagy kételkedés egy része láthatóan abból a tényből származik, hogy az elmélet szigorúan korlátozza, mi mérhető fizikailag. Tekintsük az elektron egy spinállapotát, ahogy az előbb leírtuk. Tegyük fel, hogy a spinállapot éppen |α〉, de mi ezt nem tudjuk; nem ismerjük az α irányt, amely körül az elektron a feltevés szerint pörög. Meg tudjuk-e határozni méréssel? Nem, nem tudjuk. A legtöbb, amit tehetünk, hogy szerzünk „egy bit” információt – azaz választ egyetlen igen-nem kérdésre. Kiválaszthatunk a térben egy β irányt, és mérhetjük az elektron spinjét ebben az irányban. Vagy IGEN, vagy NEM választ kapunk, de ettől kezdve elvesztettük az információt a spin eredeti irányáról. IGEN válasznál tudjuk, hogy az állapot most arányos |β〉-val, NEM válasznál tudjuk, hogy az állapot most β-val ellentétes irányú. Egyik sem mondja meg az állapot mérés előtti α irányát, csak valószínűségi információt ad α-ra.
Másrészt, úgy látszik, van valami teljesen objektív tulajdonság magáról az α irányról, amelyben az elektron „történetesen pörgött”, mielőtt a mérést elvégeztük.126 Ugyanis az elektron spinjének mérésénél választhatjuk az α irányt – és az elektron fel kell legyen készülve, hogy biztosan IGEN választ ad, ha történetesen helyesen választunk! Az az „információ”, hogy ezt a választ kell adnia, valahogy tárolva kell legyen az elektron spinállapotában.
Nekem úgy tetszik, különbséget kell tennünk aközött, hogy mi „objektív” és mi „mérhető”, amikor a fizikai valóság kérdését vizsgáljuk a kvantummechanika szerint. Egy rendszer állapotvektora nem mérhető abban az értelemben, hogy a rendszeren végrehajtott kísérletekkel nem tudunk pontosan (arányosság erejéig) megbizonyosodni arról, mi az állapot; de az állapotvektor, úgy látszik, a rendszer teljesen objektív tulajdonsága (ismét arányosság erejéig), minthogy tökéletesen jellemzik azok az eredmények, amelyeket az elvégezhető kísérletekre adnia kell. Egyetlen feles spinű részecske, mondjuk egy elektron esetében ez az objektivitás nem ésszerűtlen, mert csupán azt állítja, hogy van valamilyen irány, amelyben az elektron spinje pontosan meghatározott, bár nem tudhatjuk, melyik ez az irány. (Ám mint később látni fogjuk, bonyolultabb rendszereknél ez az „objektív” kép sokkal különösebb – már annál is, amely mindössze két feles spinű részecskéből áll.)
De szükséges-e egyáltalán, hogy legyen az elektron spinjének fizikailag meghatározott állapota a mérés előtt? Sok esetben nem lesz, mert önmagában nem lehet kvantumos rendszernek tekinteni; a kvantumállapotot általában úgy kell elkészíteni, hogy nagyszámú más részecskével együtt, azoktól elválaszthatatlanul írja le az elektront. Speciális körülmények között azonban az elektron (legalábbis a spinje) önmagában vizsgálható. Az ilyen esetekben, például amikor a spint előzőleg ténylegesen megmérték egy (esetleg ismeretlen) irányban, és ezután az elektront egy ideig semmi sem zavarta meg, a standard kvantumelmélet szerint az elektron spinjének teljesen objektíven meghatározott iránya van.
126 Ez az objektivitás abból ered, hogy komolyan vettük a szabványos kvantummechanikai formalizmust. Egy nem standard szemléletben a rendszer idő előtt „tudhatja”, milyen eredményt fog adni tetszőleges mérésre. Ez a fizikai valóság egy másféle, láthatóan objektív képéhez vezethetne.
Egy kvantumállapot másolása
Az elektron spinállapotának objektivitása, de nemmérhetősége egy másik fontos tényt példáz: lehetetlen úgy lemásolni egy kvantumállapotot, hogy az eredeti állapot érintetlen maradjon! Tegyük fel ugyanis, hogy tudunk csinálni ilyen másolatot az elektron egy |α〉 spinállapotáról. Ha meg tudtuk csinálni egyszer, akkor meg tudjuk csinálni újra meg újra. Az eredő rendszernek hatalmas impulzusmomentuma lenne egy nagyon jól meghatározott irányban. Erről az irányról, nevezetesen α-ról makroszkopikus méréssel tudomást lehetne szerezni. Ez viszont sértené az |α〉 spinállapot alapvető nemmérhetőségét.
Lehetséges azonban lemásolni egy kvantumállapotot, ha készek vagyunk az eredeti állapot megsemmisítésére. Lehet például egy elektronunk ismeretlen |α〉 spinállapotban és egy neutronunk, mondjuk egy másik, |γ〉 spinállapotban. Ezek felcserélése teljesen megengedett, ekkor a neutron spinállapota lesz |α〉, az elektroné |γ〉. Amit nem tudunk megcsinálni, az az |α〉 megkettőzése (hacsak nem tudjuk, mi az |α〉 állapot ténylegesen)! (Vö. még Wootters és Zurek 1982.)
Emlékezzünk vissza az 1. fejezetben tárgyalt „távfuvarozó gépre”. Ez azon alapult, hogy elvileg lehetséges tökéletes másolatot készíteni egy személy testéről és agyáról egy távoli bolygón. Érdekes azon elgondolkodni, hogy egy személy „tudatossága” egy kvantumállapot bizonyos sajátosságain alapulhat. Ha így van, akkor a kvantumelmélet megtiltja, hogy másolatot készítsünk e „tudatosságról” az eredeti állapot megsemmisítése nélkül – és így a távfuvarozás „paradoxonja” megoldódhat. A kvantumos jelenségek lehetséges jelentőségéről az agy működésében a két utolsó fejezetben lesz szó.
lehetetlen úgy lemásolni egy kvantumállapotot, hogy az eredeti állapot érintetlen maradjon! -írja, majd:
a személy, személyiség, és a tudat lemásolását és teleportálás-szerű elvi lehetőségét vizsgálja könyve elején, erről most itt van egy kvantumelmélettel alátámasztott következtetése:
Érdekes azon elgondolkodni, hogy egy személy „tudatossága” egy kvantumállapot bizonyos sajátosságain alapulhat. Ha így van, akkor a kvantumelmélet megtiltja, hogy másolatot készítsünk e „tudatosságról” az eredeti állapot megsemmisítése nélkül – és így a távfuvarozás „paradoxonja” megoldódhat. A kvantumos jelenségek lehetséges jelentőségéről az agy működésében a két utolsó fejezetben lesz szó.
a szirének hangja mind erősebben szól:
A kvantumos jelenségek lehetséges jelentőségéről az agy működésében a két utolsó fejezetben lesz szó.
A foton spinje
A következőkben megvizsgáljuk a foton spinjét és kapcsolatát a Riemann-gömbbel. A fotonoknak van spinjük, de mert mindig fénysebességgel mozognak, a spint nem lehet egy rögzített pontra vonatkoztatni; a spintengely mindig a mozgás iránya. A foton spinjét polarizációnak nevezik, ez az a jelenség, amelyen a „polaroid” napszemüvegek működése alapszik. Tegyünk egymásra két polaroid lemezt, és nézzünk át rajtuk. Általában azt tapasztaljuk, hogy bizonyos mennyiségű fény keresztüljut. Most forgassuk el az egyik darabot, a másikat tartsuk rögzítve. Az átjutó fény mennyisége változik. Az egyik állásban, amikor az átengedett fény maximális, a második lemez lényegében semmit nem nyel el az elsőn átjutott mennyiségből; míg az ezzel derékszöget bezáró irányban a második lemez lényegében nullára csökkenti le a fényt.
Hogy mi történik, azt legkönnyebben a fény hullámképe alapján lehet megérteni. Itt most az oszcilláló elektromos és mágneses mezőkre épülő Maxwell-féle leírásra van szükségünk. A 6.26. ábra síkban polarizált fényt illusztrál. Az elektromos mező előre-hátra oszcillál egy síkban – a polarizáció síkjában –, a mágneses mező az elektromossal megegyezően oszcillál, de vele derékszöget bezáró síkban. A polaroid lemezek olyan fényt engednek keresztül, amelynek polarizációs síkja egybeesik a lemez szerkezetével. Amikor a második lemez szerkezete ugyanolyan állású, mint az elsőé, akkor az első lemezen átjutott fény átjut a másodikon is. De amikor a két lemez szerkezete derékszögben áll egymáshoz képest, akkor a második elzárja az elsőn átjutott fény útját. Amikor a két lemez φ szögben áll egymáshoz képest, akkor a második lemez a fény
cos2φ
hányadát engedi át.
A részecskeképben minden egyedi fotonra úgy kell gondolnunk, mint amelynek van polarizációja. Az első polaroid lemez polarizációmérőként működik, IGEN választ ad, ha a foton a megfelelő irányban polarizált, ekkor átengedi a fotont. Ha a foton a „merőleges” irányban polarizált, akkor a válasz NEM, a foton elnyelődik. (Itt most a „merőleges” a Hilbert-térben a „derékszögűnek” felel meg a közönséges térben!) Feltéve, hogy a foton átmegy az első lemezen, a második lemez is ugyanazt a kérdést teszi fel neki, de más irányban. Ha a két irány által bezárt szög φ, mint az előbb, akkor cos2φ annak a valószínűsége, hogy a foton átjut a második lemezen, feltéve hogy az elsőn átjutott.
Hol kerül elő a Riemann-gömb? A polarizációs állapotok teljes, komplexszámos rendszeréhez hozzátartoznak a körkörös és elliptikus polarizációk. Ezek klasszikus hullámra a 6.27. ábrán láthatók. A körkörös (cirkuláris) polarizációnál az elektromos mező nem oszcillál, hanem forog, és a mágneses mező az elektromoshoz képest most is derékszögben, azzal egyezően forog. Az elliptikus polarizációnál a forgó és oszcilláló mozgás kombinációja jelenik meg, az elektromos mezőt leíró vektor egy ellipszist rajzol a térben. A kvantumos leírásban minden egyedi foton számára megengedettek e különböző polarizációk – a foton spinjének állapotai.
Ezután megkeressük a Riemann-gömbön a p pontot, és tekintjük azt a középponton átmenő síkot, amely merőleges a középpontot és a p pontot összekötő szakaszra. Ez a sík a gömböt egy körben metszi, e kört függőlegesen levetítve megkapjuk a polarizációs ellipszist (6.28. ábra).127 A q Riemann-gömb leírja a foton polarizációs állapotainak rendszerét, de a térbeli irányítást q négyzetgyöke, p adja meg.
A valószínűségek számítására ugyanazt az
képletet használhatjuk, mint az elektron esetében, csak most q-ra kell alkalmazni és nem p-re. Tekintsük a síkbeli polarizációt. Megmérjük először egy irányban a foton polarizációját, utána egy azzal φ szöget bezáró másikban; e két irány két p értéknek felel meg a gömb egyenlítőjén, a közöttük lévő szög φ. Minthogy a p-k a q-k négyzetgyökei, ezért a q pontok közötti θ szög kétszerese a p pontok közöttinek: θ = 2φ. Így az IGEN valószínűsége a második mérésnél, feltéve hogy az első eredménye IGEN volt (azaz hogy a foton átjut a második lemezen, miután az elsőn már átjutott),
, ami (egyszerű trigonometriai számolással igazolhatóan) ugyanaz, mint a korábban megadott cos2φ.
127 A –p komplex szám ugyanúgy megfelel, mint q négyzetgyöke, és ugyanazt a polarizációs ellipszist adja. A négyzetgyökvonás azzal függ össze, hogy a foton tömeg nélküli egyes spinű részecske, azaz spinje az alapvető egység, ħ/2 kétszerese. Egy gravitonnak – a gravitáció eddig még nem észlelt, tömeg nélküli kvantumának – a spinje kettő lenne, azaz négyszerese az alapegységnek, ekkor a fentihez hasonló leírásban q negyedik gyökét kellene vennünk.
Nagy spinű objektumok
Az olyan kvantumrendszerben, amelyben a bázisállapotok száma kettőnél nagyobb, a fizikailag megkülönböztethető állapotok tere a Riemann-gömbnél sokkal bonyolultabb. Azonban a spin esetében magának a Riemann-gömbnek mindig közvetlen geometriai szerepe van. Tekintsünk egy nyugalomban lévő, tömeges részecskét vagy atomot, amelynek spinje n ∙ ħ/2. Ez a spin egy (n + 1) állapotú kvantumrendszert definiál. (Tömeg nélküli spines részecskénél, azaz olyannál, amely fénysebességgel mozog, akár a foton, a spin mindig kétállapotú rendszer, ahogy az előbb leírtuk. Tömeggel rendelkezőnél azonban az állapotok száma a spinnel nő.) Ha ezt a spint valamilyen irányban megmérjük, akkor (n + 1) különböző lehetséges eredményt tapasztalunk, attól függően, milyen mértékben áll a spin ebben az irányban. A ħ/2 alapegységben kifejezve a spin lehetséges értékei ebben az irányban n, n – 2, n – 4, … , 2 – n vagy –n. Így n = 2-re az értékek 2, 0 vagy –2; n = 3-ra 3, 1, –1 vagy –3; stb. A negatív értékek annak felelnek meg, hogy a spin a mérési iránnyal inkább ellentétes. A feles spin, azaz n = 1 esetében az 1 érték az IGEN, a –1 a NEM válasznak felel meg az előző leírás szerint.
Az a helyzet – az okokat nem kívánom elmagyarázni (Majorana 1932, Penrose 1987a) –, hogy nħ/2 spin esetén minden spinállapot (arányosság erejéig) egyértelműen jellemezhető egy n pontból álló (nem rendezett) halmazzal a Riemann-gömbön – azaz a (rendszerint különböző), a középpontból kifelé mutató iránnyal (lásd 6.29. ábra). (Ezeket az irányokat a rendszeren végrehajtható mérések jellemzik: ha az egyikben megmérjük a spint, akkor az eredmény biztosan nem az, hogy teljesen az ellentétes irányba mutat, azaz az n, n – 2, n – 4, …, 2 – n értékek egyikét adja, –n-et nem.) Az n = 1 speciális esetben, mint előbb az elektronnál, egy pontunk van a Riemann-gömbön, ez a q-val jelölt pont az előző leírásban. Nagyobb spinértékekre azonban a kép bonyolultabb, olyan, mint ahogy előbb leírtam – bár ez a kép a fizikusok körében bizonyos okok miatt nem túl népszerű.
Van valami nagyon figyelemreméltó és rejtélyes ebben a leírásban. Gyakran elhitetik velünk, hogy megfelelően korlátozott értelemben az atomok (vagy elemi részecskék vagy molekulák) kvantumos leírása szükségszerűen átmegy a klasszikus newtoniba, amikor a rendszer naggyá és bonyolulttá válik. Ám ez így, ahogy van, egyszerűen nem igaz. Egy nagy impulzusmomentumú objektum spinállapotai ugyanis, amint láttuk, nagyszámú elszórt pontnak felelnek meg a Riemann-gömbön.128 Azt gondolhatjuk, hogy az objektum spinje egy csomó feles spinből tevődik össze, amelyek e pontok által meghatározott különböző irányokba mutatnak. E kombinált állapotok közül csak néhány – nevezetesen azok, amelyekben a pontok legtöbbje a gömb egy kis tartományában sűrűsödik össze (azaz, amelyekben a legtöbb feles spin durván ugyanabba az irányba mutat) – felel meg olyan tényleges impulzusmomentum-állapotnak, amilyenekkel klasszikus objektumoknál, például krikettlabdáknál rendesen találkozunk. Azt várhatnánk, hogy ha kiválasztunk egy olyan spinállapotot, amelyben a teljes spin értéke (ħ/2 egységekben) nagyon nagy szám, de egyébként „véletlenszerű”, akkor valami a klasszikus spinhez hasonló mutatkozik. Ám a dolgok egyáltalán nem így állnak. Általában a nagy, teljes spinű kvantumos spinállapotok semmi hasonlóságot nem mutatnak a klasszikusakhoz!
Hogy is néz ki akkor a megfeleltetés a klasszikus fizika impulzusmomentumával? Noha a legtöbb nagy spinű kvantumállapot nem emlékeztet klasszikus állapotokra, ezek olyan (ortogonális) állapotok lineáris kombinációi, amelyek mindegyike egy klasszikusra emlékeztet. A rendszer valahogyan végrehajt magán egy „mérést”, és az állapot (bizonyos valószínűséggel) „beugrik” az egyik vagy másik ilyen klasszikusszerű állapotba. Nem csak az impulzusmomentummal van így, hasonló a helyzet a rendszer egyéb klasszikusan mérhető tulajdonságaival is. A kvantummechanika e vonatkozásának kell belépnie, amikor egy rendszer „eléri a klasszikus szintet”. Később majd többet mondok erről, de mielőtt az ilyen „nagy” vagy „bonyolult” kvantumrendszereket tárgyalhatnánk, kell hogy legyen valami érzésünk arról a rendkívüli módró1, ahogyan a kvantummechanika az egynél több részecskét tartalmazó rendszereket kezeli.
128 Helyesebben mondva: az impulzusmomentumot különböző számú pont ilyen elrendezéseinek komplex lineáris kombinációja írja le, mert egy bonyolult rendszer esetében több különböző teljes spinérték szuperponálódhat. Ezért a teljes kép még kevésbé hasonlít a klasszikus impulzusmomentumhoz!
Sokrészecskés rendszerek
A sokrészecskés állapotok kvantummechanikai leírása sajnos meglehetősen bonyolult. Alkalmasint egész szélsőségesen komplikált lehet. Az összes részecske összes lehetséges különböző helyzetének szuperpozícióiban kell gondolkodnunk! Ez a lehetséges állapotok hatalmas terét adja – sokkal nagyobbat, mint amilyet a klasszikus elmélet egy mezője jelent. Láttuk, hogy egyetlen részecske kvantumállapota, nevezetesen egy hullámfüggvény, is annyira bonyolult, mint egy teljes klasszikus mező. Már ez a kép (amelynek megadásához végtelen számú paraméter szükséges) jóval bonyolultabb, mint egy részecske klasszikus képe (amely állapotának megadásához csak néhány adat kell – hat, ha nincsenek belső szabadsági fokok, mint a spin; vö. 5. fejezet). Már ez elég rosszul néz ki, és azt gondolhatnánk, hogy két részecske kvantumállapotának leírásához két „mezőre” van szükség, mindegyik részecske leírásához egy-egyre. Egyáltalán nem így van! Két vagy több részecske esetén az állapot leírása messze bonyolultabb ennél, mint azt hamarosan látni fogjuk.
Egyetlen (spin nélküli) részecske kvantumállapotának meghatározásában a részecske által elfoglalható minden egyes lehetséges helyzethez tartozik egy komplex szám (amplitúdó). Van amplitúdója annak, hogy a részecske az A pontnál van, hogy a B pontnál van, hogy a C pontnál van stb. Gondoljunk most két részecskére. Az első lehet A-nál, a második mondjuk B-nél. Kell legyen egy amplitúdója ennek a lehetőségnek. Fordítva, lehet az első részecske B-nél, a második A-nál, ennek is kell legyen amplitúdója; vagy lehet az első B-nél, a második C-nél; vagy mindkettő A-nál. Ezen alternatívák mindegyikéhez kell tartozzon egy amplitúdó. A hullámfüggvény ezért nem két helyfüggvény (azaz két mező); a két helyzetnek egy függvénye!
Hogy elképzelésünk legyen arról, mennyivel bonyolultabb előírni két helyváltozó egy függvényét, mint egy helyváltozó két függvényét, képzeljünk el egy esetet, amelyben a lehetséges helyzetek csak egy véges halmazt alkotnak. Tegyük fel, hogy tíz megengedett helyzet van, ezeket a
|0〉, |1〉, |2〉, |3〉, |4〉, |5〉, |6〉, |7〉, |8〉, |9〉
(ortogonális) állapotok adják meg. Egyetlen részecske |ψ〉 állapota ezek
|ψ〉 = z0|0〉 + z1|1〉 + z2|2〉 + z3|3〉 + … + z9|9〉
kombinációja, ahol a z0, z1, z2, z3, …, z9 együtthatók adják a megfelelő amplitúdókat. A részecske állapotát tíz komplex szám írja le. Egy kétrészecske-állapotnál minden helyzetpárhoz kell egy amplitúdó. Összesen
102 = 100
különböző (rendezett) helyzetpár van, így száz komplex számra van szükségünk! Ha csak két egyrészecske-állapotunk volna (azaz két „egyváltozós függvényünk” a fenti „egy kétváltozós függvény” helyett), akkor csak húsz komplex számra volna szükségünk.
E száz számra a
z00, z01, z02, …, z09, z10, z11, z12, …, z20, …, z99,
a megfelelő (ortonormált) bázisvektorokra a129
|0〉|0〉, |0〉|1〉, |0〉|2〉, …, |0〉|9〉, |1〉|0〉, …, |9〉|9〉
jelöléseket használhatjuk. A |ψ〉 általános kétrészecske-állapot általános alakja a következő:
|ψ〉 = z00|0〉|0〉 + z01|0〉|1〉 + … + z99|9〉|9〉.
Az állapotok e „szorzat”-jelölésének jelentése a következő: ha |α〉 az első részecske egy lehetséges állapota (nem szükségszerűen helyzetállapot), és ha |β〉 a második részecske egy lehetséges állapota, akkor az az állapot, amely szerint az első részecske |α〉 és a második részecske |β〉 állapotban van,
|α〉|β〉.
Bármely más kvantumállapotpár között lehet „szorzatot” képezni, nem csak egyrészecske-állapotok között. Az |α〉|β〉 szorzatállapotot (amelynek tényezői nem feltétlenül egyrészecske-állapotok) mindig úgy értelmezzük, mint amely a
„ha az első rendszer állapota |α〉 és a második rendszer állapota |β〉”
kapcsolatot írja le. (Hasonlóan értelmezzük az |α〉|β〉|γ〉 stb. állapotokat; lásd alább.) Azonban az általános kétrészecske-állapot nem ilyen „szorzat” alakú. Lehet például
|α〉|β〉 + |ρ〉|σ〉,
ahol |ρ〉 az első rendszer, |σ〉 a második rendszer egy másik lehetséges állapota. Ez az állapot egy lineáris szuperpozíció; nevezetesen az első kapcsolat |α〉 és|β〉) plusz a második kapcsolat |ρ〉 és|σ〉, és nem fejezhető ki egyszerű szorzatként (azaz két állapot kapcsolataként). Egy másik példa, az |α〉|β〉 – i|ρ〉|α〉 állapot egy másik lineáris szuperpozíciót írna le. Jegyezzük meg, hogy a kvantummechanika szerint meg kell őrizni a világos különbséget az „és” és a „plusz” szavak jelentése között. Nagyon szerencsétlen modern irányzat – például a biztosítási füzetekben – a „plusz” rossz „és” értelmű használata. Itt most sokkal gondosabbnak kell lennünk!
Három részecskével a helyzet nagyon hasonló. Hogy az előző feltételek mellett, amikor csak tíz helyzet lehetséges, megadjunk egy általános háromrészecske-állapotot, ahhoz ezer komplex számra van szükségünk! A háromrészecske-állapotok egy teljes bázisa a következő lehet:
|0〉|0〉|0〉, |0〉|0〉|1〉, |0〉|0〉|2〉, …, |8〉|9〉|9〉, |9〉|9〉|9〉.
Vannak
|α〉|β〉|γ〉
alakú speciális háromrészecske-állapotok (ahol |α〉, |β〉 és |γ〉 nem feltétlenül helyzetállapotok), de az általános háromrészecske-állapot sok ilyen „szorzatállapot” szuperpozíciója. A minta a négy- és többrészecske-állapotokra ezek után világos.
Mindeddig csak megkülönböztethető részecskékről beszéltünk, amelyeknél az „első részecske”, „második részecske”, „harmadik részecske” stb. mind különböző típusú. A kvantummechanika egyik meglepő tulajdonsága azonban az, hogy azonos részecskékre más szabályok érvényesek. Ezen szabályok szerint világos, hogy valamely speciális típusú összes részecskének pontosan azonosaknak kell lenniük egymással, nem csak mondjuk nagyon hasonlóaknak. Ez vonatkozik minden elektronra és minden fotonra. Ám, amint kiderül, az összes elektron másképpen azonos egymással, mint az összes foton egymással! A különbség abban a tényben van, hogy az elektronok fermionok, míg a fotonok bozonok. A részecskék e két általános típusát egymástól meglehetősen különbözően kell kezelnünk.
Mielőtt a szóbeli pontatlanságokkal teljesen összezavarnám az Olvasót, hadd magyarázzam el, hogyan is kell ténylegesen jellemezni a fermion- és a bozonállapotokat. A szabály a következő. Ha |ψ〉 olyan állapot, amely valahány speciális típusú fermiont tartalmaz, akkor bármely két fermion felcserélésének a
|ψ〉 → –|ψ〉
változással kell együtt járnia. Ha |ψ〉 valahány speciális típusú bozont tartalmaz, akkor bármely két bozon felcserélése változatlanul kell hagyja |ψ〉-t:
|ψ〉 → |ψ〉.
Ezek egyik velejárója, hogy két fermion nem lehet ugyanabban az állapotban. Ha ugyanis ez volna a helyzet, akkor felcserélésük nem változtatná meg a teljes állapotot, ezért igaz volna, hogy –|ψ〉 = |ψ〉, azaz hogy |ψ〉 = 0, ami nem megengedett egy kvantumállapotra. Ez a tulajdonság a Pauli-féle kizárási elv130 néven ismert, és következményei az anyag szerkezetét illetően alapvetőek. Az anyag összes fő alkotórésze fermion: elektronok, protonok és neutronok. A kizárási elv nélkül az anyag összeroskadna saját magába!
Vizsgáljuk meg újra tíz helyzetünket; tegyük most fel, hogy van egy két azonos fermiont tartalmazó állapotunk. A |0〉|0〉 állapotot a Pauli-elv kizárja (az első és második tényező felcserélésekor nem negatívjába megy át, hanem saját magába). Továbbmenve: |0〉|1〉 sem felel meg így, ahogy van, mert a felcseréléskor nem negatívjába megy át; ez azonban könnyen orvosolható, ha a
|0〉|1〉 – |1〉|0〉
állapottal helyettesítjük. (Normálősi célokból, ha akarjuk, kiegészíthetjük egy általános
szorzótényezővel.) Ez az állapot az első és második részecske felcserélésekor helyesen előjelet vált, de most |0〉|1〉 és |1〉|0〉 nem független állapotok. A kettő helyett most csak egy állapotunk van! Összesen (10 ∙ 9)/2 = 45 ilyen állapotunk van, egy a |0〉, |1〉, …, |9〉 különböző állapotokból képezett minden rendezetlen párra. Így 45 komplex számra van szükségünk ahhoz, hogy rendszerünkben megadjunk egy kétfermion-állapotot. Három fermionnál három különböző helyzetre van szükség, és a bázisállapotok hasonlóak, mint a
|0〉|1〉|2〉 + |1〉|2〉|0〉 + |2〉|0〉|1〉 – |0〉|2〉|1〉 – |2〉|1〉|0〉 – |1〉|0〉|2〉
állapot, összesen (10 ∙ 9 ∙ 8)/6 = 120 ilyen állapot van; így egy háromfermion-állapot megadásához 120 komplex szám szükséges. Hasonló a helyzet nagyobb számú fermion esetén is.
Egy pár azonos bozonra a független bázisállapotok kétfélék, nevezetesen
|0〉|1〉 + |1〉|0〉
és
|0〉|0〉
alakú állapotok (utóbbiak most megengedettek), összesen (10 ∙ 11)/2 = 55. A kétbozon-állapothoz így 55 komplex számra van szükség. Három bozon esetén három különböző típusú bázisállapot van, és (10 ∙ 11 ∙ 12)/6 = 220 komplex szám szükséges; és így tovább.
Természetesen itt most egy egyszerűsített helyzetet vizsgáltam, hogy a fő gondolatokat elmondjam. A realisztikusabb leírás megkövetelné a helyzetállapotok egy teljes kontinuumát, de a lényeges szempontok azonosak. Egy másik csekély bonyodalmat jelent a spin. Egy feles spinű részecskének (tehát fermionnak) minden helyzetben két lehetséges állapota van. Használjuk ezekre a „↑” („spin fel”) és „↓” („spin le”) jelölést. Így egyszerűsített esetünkben egyetlen részecskének nem tíz, hanem húsz bázisállapota volna:
|0 ↑〉, |0 ↓〉, |1 ↑〉, |1 ↓〉, |2 ↑〉, |2 ↓〉 …, |9 ↑〉, |9 ↓〉,
de ettől eltekintve az eljárás ugyanúgy megy, mint előbb (így két ilyen fermionnál (20 ∙ 19)/2 = 190, háromnál (20 ∙ 19 ∙ 18)/6 = 1140 stb. számra van szükségünk).
Az 1. fejezetben hivatkoztam arra a tényre, hogy a modern elmélet szerint egyáltalán semmi nem történne, ha egy ember testének egy részecskéjét kicserélnénk egy házának falában lévő hasonló részecskével. Ha ez a részecske bozon, akkor, mint láttuk, a |ψ〉 állapot valóban teljesen változatlan. Ha fermion, akkor a |ψ〉 állapot –|ψ〉-re változik, amely fizikailag azonos |ψ〉-vel. (Ha szükségét érezzük, orvosolhatjuk az előjelváltást úgy, hogy a felcserélés közben az egyik részecskét 360°-kal elforgatjuk. Emlékezzünk vissza, hogy az ilyen forgatásnál a fermionok előjelet váltanak, a bozonok változatlanok maradnak!) A modern elmélet (úgy 1926 óta) valóban mond valami mélyet a fizikai anyag darabjai egyedi azonosságának kérdéséről. Szigorúan véve nem hivatkozhatunk „erre a speciális elektronra” vagy „arra az egyedi fotonra”. Amikor azt mondjuk, hogy „az első elektron itt van, a második amott”, akkor azt állítjuk, hogy az állapot |0〉|1〉 alakú, ami, mint láttuk, fermionállapotra nem megengedett! Mondhatjuk azonban azt, hogy „az elektronpár egyik tagja itt van, a másik amott”. Lehet beszélni az összes elektron vagy összes proton, vagy összes foton konglomerátumáról (bár még ekkor is figyelmen kívül hagyjuk a különböző típusú részecskék kölcsönhatásait). Az egyedi elektronok e teljes kép egy közelítését adják, ugyanúgy, mint az egyedi protonok vagy egyedi fotonok. E közelítés a legtöbb esetben jól működik, de vannak olyan helyzetek, amikor nem: a szupravezetés, a szuperfolyékonyság és a lézer viselkedése említésre méltó ellenpéldák.
A fizikai világ képe, ahogy azt a kvantummechanika elénk tárja, egyáltalán nem az, amihez a klasszikus fizikában hozzászoktunk. De kapaszkodjon jól meg az Olvasó – még furcsább dolgok is vannak a kvantumvilágban!
129 Matematikai nyelven azt mondjuk, hogy a kétrészecske-állapotok tere az első és a második részecske állapotai terének tenzorszorzata. A ∣χ〉∣φ〉 állapot ekkor a ∣χ〉 és ∣φ〉 állapotok tenzorszorzata.
130 Wolfgang Pauli, a ragyogó osztrák fizikus, a kvantummechanika fejlődésének kiemelkedő személyisége kizárási elvét mint hipotézist vetette fel 1925-ben. Amit ma „fermionoknak” nevezünk, annak teljes kvantummechanikai kezelését 1926-ban dolgozta ki a nagyhatású és eredeti olasz-amerikai fizikus, Enrico Fermi és a kiváló Paul Dirac, akinek nevével korábban már többször találkoztunk. A fermionok statisztikus viselkedését a „Fermi–Dirac-statisztikák” írják le, a megkülönböztethető részecskék klasszikus, „Boltzmann-statisztikájától” eltérően. A bozonok „Bose–Einstein-statisztikáját” a fotonok kezelésére dolgozta ki 1924-ben a neves indiai fizikus, S. N. Bose és Albert Einstein.
Einstein, Podolsky és Rosen „paradoxonja”
Mint e fejezet elején említettem, Albert Einstein egyes elképzelései egészen alapvetőek voltak a kvantumelmélet fejlődésében. Emlékezzünk rá, hogy ő vezette be először a „foton” – az elektromágneses mező kvantuma – fogalmát, már 1905-ben, és ebből fejlődött ki a hullám–részecske dualitás. (Részben tőle származik a „bozon” fogalma is, mint annyi más, az elmélet szempontjából központi gondolat.) Mégsem volt képes soha elfogadni, hogy az elmélet, amely később e gondolatokból kifejlődött, nem csak átmenetileg lehet a fizikai világ leírása. Idegenkedése az elmélet valószínűségi vonatkozásától jól ismert, benne van Max Born egyik levelére 1926-ban írott válaszában (hivatkozás Pais 1982-ben, 443. o.):
A kvantummechanika nagyon meggyőző. Ám egy belső hang azt súgja nekem, hogy ez még nem az igazi. Az elmélet nagyon sokat tud, de aligha visz közelebb az Öreg titkához. Mindenesetre meg vagyok győződve arról, hogy Ő nem játszik kockajátékot.
Ám úgy látszik, Einsteint leginkább, e fizikai indeterminizmusnál még sokkal jobban, az objektivitás látható hiánya zavarta abban a módban, ahogy a kvantumelméletet látszólag le kell írni. A tárgyalás során nem sajnáltam a fáradságot annak hangsúlyozására, hogy a világ leírása az elmélet szerint valójában egészen objektív, bár gyakran nagyon különös, és ellenkezik az intuícióval. Másrészt Bohr úgy tekintett egy rendszer kvantumállapotára, mint amelynek (a mérések között) nincs fizikai realitása, csupán összegzése a rendszerre vonatkozó „tudásunknak”. Nem lehet-e azonban különböző megfigyelőknek eltérő tudásuk egy rendszerről, nem látszik-e így a hullámfüggvény lényegesen szubjektívnek? Nincs-e csupán „az egész a fizikus fejében”? Nem engedhetjük meg, hogy csodálatosan pontos fizikai képünk a világról, ahogy az évszázadok alatt kifejlődött, tökéletesen elillanjon; Bohrnak ezért a klasszikus szinten kellett néznie a világot, hogy ténylegesen legyen objektív valósága. Az egész alapjául szolgáló, kvantumszintű állapotoknak már nem volna „valóságuk”.
Ez a kép rémítő volt Einstein számára, aki hitte, hogy kell lennie egy objektív fizikai világnak még a kvantumos jelenségek legparányibb skáláján is. Bohrral folytatott számos vitájában be akarta bizonyítani (de nem sikerült neki), hogy a dolgok kvantumos képében inherens ellentmondások vannak, ezért a kvantumelmélet mögött kell lennie egy még mélyebb szerkezetnek, amely valószínűleg jobban hasonlít a klasszikus fizika által szolgáltatott képhez. A kvantumos rendszerek valószínűségi viselkedésének hátterében esetleg a rendszer kisebb „részeinek” statisztikus működése lehet, amelyről nincs közvetlen tudomásunk. Einstein követői, elsősorban David Bohm, kidolgozták a „rejtett változók” elméletét, amely szerint valóban volna határozott realitás, de a rendszert pontosan meghatározó paraméterek közvetlenül nem hozzáférhetőek számunkra, a kvantumos valószínűségek azért keletkeznek, mert e paraméterek értékei a mérés előtt ismeretlenek.
Összhangban lehet-e egy ilyen rejtettváltozós elmélet a kvantumfizika minden megfigyelt jelenségével? A válasz, úgy látszik, igen, de csak akkor, ha az elmélet lényegesen nemlokális, távolba ható abban az értelemben, hogy a rejtett paraméterek képesek kell legyenek pillanatszerűen befolyásolni a rendszer tetszőlegesen távoli részeit! Ez nem tetszett volna Einsteinnek, különösen nem a speciális relativitáselmélettel kapcsolatos nehézségek miatt. Ezekről később lesz szó. A legsikeresebb rejtettváltozó-elmélet a de Broglie–Bohm-modell néven ismert (de Broglie 1956, Bohm 1952). Ezeket a modelleket nem fogom tárgyalni, mert célom az, hogy e fejezetben csak a standard kvantumelméletről adjak áttekintést, és nem a különféle rivális javaslatokról. Ha fizikai objektivitást kívánunk, de készek vagyunk nélkülözni a determinizmust, akkor a standard elmélet önmagában kielégítő. Az állapotvektort úgy tekintjük, mint ami a „valóságot” adja meg – és általában a sima, determinisztikus U eljárás szerint fejlődik, de hébe-hóba furcsán „ugrik” R szerint, amikor csak egy jelenséget kinagyítunk a klasszikus szintre. A távolbahatás problémája és a látható nehézségek a relativitáselmélettel azonban megmaradnak. Vessünk ezekre egy pillantást!
Tegyük fel, hogy van egy fizikai rendszerünk, amely két alrendszert tartalmaz, A-t és B-t. Legyen például A és B két különböző részecske! Tegyük fel, hogy A két lehetséges (ortogonális) állapota |α〉 és |ρ〉, míg B állapota |β〉 és |σ〉 lehet. Mint az előbbiekben láttuk, az általános kombinált állapot nem egyszerűen A állapotának és B állapotának szorzata („és”), hanem ilyen szorzatok egy szuperpozíciója („plusz”). (Azt mondjuk, hogy A és B között korreláció van.) Legyen a rendszer állapota
|α〉|β〉 + |ρ〉|σ〉.
Végezzünk most egy igen-nem mérést A-n, amely megkülönbözteti |α〉-t (IGEN) és |ρ〉-t (NEM). Mi történik B-vel? Ha a mérés eredménye IGEN, akkor az eredő állapot
|α〉|β〉
kell legyen, ha az eredmény NEM, akkor
|ρ〉|σ〉.
Így az A-n végzett mérésünk B állapotát ugrasztja: |β〉-ba IGEN, |σ〉-ba NEM válasz esetén! A B részecskének nem kell az A közelében lennie; lehet attól fényévekre is. Mégis az A-n végzett méréssel egyidejűen B ugrik!
Álljunk csak meg! – mondhatja az Olvasó. – Mi ez az állítólagos „ugrás”? Miért nem a következőképpen mennek a dolgok? Képzeljünk el egy dobozt, benne egy fehér és egy fekete golyóval. Tegyük fel, hogy a golyókat kivettük, és anélkül, hogy bármelyikre ránéztünk volna, letesszük azokat a szoba két ellentétes sarkába. Ha ekkor megvizsgáljuk az egyiket és azt találjuk, hogy fehér (mint az előbb „|α〉”), akkor – csiribí-csiribá – a másik fekete (az előbb |β〉)! Ha viszont az elsőt feketének találjuk („|ρ〉”), akkor a második golyó bizonytalan állapota egy pillanat alatt beugrik a „biztos fehérbe” („|σ〉”). Senki sem tulajdonítaná – makacskodik az Olvasó – a második golyó „bizonytalan” állapotának hirtelen átváltozását „biztos feketévé” vagy „biztos fehérré” valamilyen titokzatos távolba ható „befolyásnak”, amely pillanatszerűen jut el hozzá az első golyótól, amikor azt megvizsgáljuk.
A Természet azonban sokkal rendkívülibb ennél. Az előzőeknél valóban elképzelhetjük, hogy a rendszer már „tudta”, hogy mondjuk B állapota |β〉 és A-é |α〉, (vagy B-é |σ〉 és A-é |ρ〉), mielőtt a mérést A-n végrehajtottuk volna; és csak arról volt szó, hogy a kísérletező nem tudta. Amikor A-t az |α〉 állapotban találja, egyszerűen következtet, hogy B |β〉-ban van. Ez lenne a „klasszikus” nézőpont – mint egy lokális, rejtettváltozós elméletben – mindenféle fizikai ugrás nélkül. (Minden a kísérletező fejében történik!) E nézet szerint a rendszer minden egyes része előre „tudja” bármilyen rajta végrehajtható kísérlet eredményét. Valószínűségek csak a kísérletező tudásának hiánya miatt lépnek fel. Érdekes módon kiderül, hogy ez a nézőpont nem szolgáltat magyarázatot a kvantumelméletben fellépő összes rejtélyes, láthatóan nemlokális valószínűségre!
Hogy ezt felfogjuk, tekintsünk egy, az előzőhöz hasonló helyzetet, csak most az A rendszeren végzett mérés megválasztása ne legyen eldöntve mindaddig, amíg A és B nincs jól szétválasztva. Ekkor úgy látszik, hogy maga a döntés befolyásolja pillanatszerűen B viselkedését! Ez a látszólag paradox, „EPR”-típusú „gondolatkísérlet” Albert Einsteintől, Boris Podolskytól és Nathan Rosentól származik (1935). Ennek egy David Bohmtól (1951) származó változatát fogom ismertetni. Az az állítás, hogy lokális, „realisztikus” (azaz rejtettváltozós vagy „klasszikus típusú”) leírás nem képes megadni a helyes kvantumos valószínűségeket, John S. Bell egy nevezetes tételéből következik (lásd Bell 1987, Rae 1986, Squires 1986).
Tegyük fel, hogy egy középpontban lévő, zérus spinű részecske bomlásakor két feles spinű részecske keletkezik – elektronnak (e–) és pozitronnak (e+) (azaz antielektronnak) fogom nevezni ezeket –, és ellentétes irányban mozognak közvetlenül kifelé (6.30. ábra). Az impulzusmomentum megmaradása miatt az elektron és pozitron spinjeinek összege zérust ad, mert ennyi volt kezdetben a középső részecske impulzusmomentuma. Ennek az a következménye, hogy amikor tetszőlegesen választott irányban megmérjük az elektron spinjét, akkor a pozitron spinje az elektronéval ellentétes irányba kell mutasson! A két részecske mérföldekre, sőt fényévekre lehet egymástól, mégis maga az egyik részecskén végzett mérés megválasztása, úgy látszik, pillanatszerűen rögzíti a másik spinjének tengelyét!
|Q〉 = |E ↑〉|P ↓〉 – |E ↓〉|P ↑〉,
összefüggést találjuk, ahol E az elektront, P a pozitront jelenti. A leírás most a spin fel/le irányai szerint történik. A teljes állapot lineáris szuperpozíciója annak, amelyben az elektron spinje felfelé és a pozitron spinje lefelé és amelyben az elektron spinje lefelé és a pozitron spinje felfelé áll. Ezért ha megmérjük az elektron spinjét a fel/le irányban, és azt találjuk, hogy felfelé mutat, akkor az |E ↑〉|P ↓〉 állapotba kell ugranunk, tehát a pozitron „le” spinállapotú kell legyen. Ha viszont azt találjuk, hogy az elektron spinje lefelé mutat, akkor az állapot az |E ↑〉|P ↓〉-be ugrik, tehát a pozitron spinje felfelé mutat.
Tegyük most fel, hogy választottunk egy másik ellentétes iránypárt, legyen ez mondjuk a jobb és bal, ahol
|E →〉 = |E ↑〉 + |E ↓〉, | |P →〉 = |P ↑〉 + |P ↓〉 |
és
|E ←〉 = |E ↑〉 – |E ↓〉, | |P ←〉 = |P ↑〉 – |P ↓〉 |
ekkor fennáll (ha akarja, ellenőrizze az algebrát!), hogy
|E →〉|P ←〉 – |E ←〉|P →〉 = (|E ↑〉 + |E ↓〉)(|P ↑〉 – |P ↓〉) – (|E ↑〉 – |E ↓〉)(|P ↑〉 + |P ↓〉) = |E ↑〉|P ↑〉 + |E ↓〉|P ↑〉 – |E ↑〉|P ↓〉 – |E ↓〉|P ↓〉 – |E ↑〉|P ↑〉 + |E ↓〉|P ↑〉 – |E ↑〉|P ↓〉 + |E ↓〉|P ↓〉 = –2(|E ↑〉|P ↓〉 – |E ↓〉|P ↑〉) = –2|Q〉,
amely (a lényegtelen –2 szorzótól eltekintve) ugyanaz az állapot, amelyből indultunk. Így eredeti állapotunk ugyanúgy gondolható egy jobbra pörgő elektron és egy balra pörgő pozitron, illetve egy balra pörgő elektron és egy jobbra pörgő pozitron lineáris szuperpozíciójának! E kifejezés akkor hasznos, ha az elektron spinjének mérésére nem a fel/le, hanem a jobb/bal irányt választjuk. Ha azt találjuk, hogy valóban jobbra pörög, akkor az állapot |E →〉|P ←〉-ba ugrik, azaz a pozitron balra pörög. Ha viszont azt találjuk, hogy az elektron balra pörög, akkor az állapot |E ←〉|P →〉-ba ugrik, tehát a pozitron jobbra pörög. Ha az elektron spinjének mérésére tetszőleges más irányt választottunk volna, a történet pontosan ennek megfelelő lett volna: a pozitron spinállapota pillanatszerűen ugrana vagy ebbe az irányba, vagy az ellentétesbe, az elektronon végzett mérés eredményétől függően.
Miért nem modellezhetjük elektronunk és pozitronunk spinjét az előbb elmondott példához, a dobozból kivett fekete és fehér golyóhoz hasonlóan? Legyünk teljesen általánosak. Fekete és fehér golyó helyett lehet két gépezetünk, E és P, amelyek kezdetben egyesítve vannak, majd ellentétes irányban mozognak. Tegyük fel, hogy E is, P is IGEN vagy NEM választ tud adni tetszőleges irányban végzett spinmérésre. E válasz a gépezet által teljesen meghatározott lehet minden irányválasztás mellett – vagy esetleg a gépezet csak valószínűségi válaszokat ad, és a valószínűségeket határozza meg –, de mindenképpen feltételezzük, hogy szétválasztás után E és P egymástól teljesen függetlenül viselkedik.
Spinmérőink vannak mindkét oldalon, az egyik E, a másik P spinjét méri. Tegyük fel, hogy mindkettőben három állás van a spin irányának mérésére, mondjuk A, B, C az E-mérőben, A’, B’, C’ a P-mérőben. Az A’, B’ és C’ irányok rendre párhuzamosak az A, B, és C irányokkal, utóbbiakat egy síkban vesszük fel és úgy, hogy egymással egyenlő, tehát 120°-os szöget zárjanak be (lásd 6.31. ábra). Képzeljük most el, hogy a kísérletet mindkét oldalon különböző irányokban sokszor megismételjük. Az E-mérő olykor IGEN választ jegyez fel (azaz a mérés A vagy B vagy C irányába mutató spint), olykor NEM választ (ellentétes irányú spint). A P-mérő hasonlóképpen néha IGEN, néha NEM választ rögzít. A tényleges kvantumos valószínűségeknek mutatniuk kell a következő két tulajdonságot:
1. Ha a két oldal állásai (azaz A és A’ stb.) azonos irányúak, akkor a két mérő eredményei mindig ellentétesek (azaz az E-mérő IGEN választ észlel, amikor a P-mérő NEM-et, és NEM-et, amikor a P IGEN-t.)
2. Ha az állások tárcsáit elforgatjuk, és egymástól teljesen függetlenül véletlenszerűen állítjuk be, akkor a két mérő eredménye egyenlő valószínűséggel egyező vagy ellentétes.
Könnyen beláthatjuk, hogy az (1) és (2) tulajdonságok közvetlenül adódnak a korábban leírt kvantumos valószínűségi szabályokból. Feltehetjük, hogy először az E-mérő működik. A P-mérő ekkor olyan részecskét észlel, amelynek spinállapota ellentétes az E-mérő által észlelttel, az (1) tulajdonság tehát azonnal következik. Hogy a (2) tulajdonságot megkapjuk, megjegyezzük, hogy 120°-os szöget bezáró mérési irányok mellett, ha az E-mérő IGEN-t ad, akkor a P-irány 60°-os szöget zár be a P által mért spinállapot irányával, ha NEM-et, akkor 120°-osat. Ezért 3/4 = 1/2(1 + cos60°) a valószínűsége annak, hogy a mérések megegyeznek, és 1/4 = 1/2(1 + cos120°) a valószínűsége annak, hogy ellentétesek. Így amikor E IGEN-t ad, akkor P IGEN válaszának a három P-állásra átlagolt valószínűsége 1/3(0 + 3/4 + 3/4) = 1/2, P NEM válaszának pedig 1/3(1 + 1/4 + 1/4) = 1/2 – azaz egyformán valószínűen egyeznek és nem egyeznek –, és hasonló a helyzet, ha E NEM-et ad. Ez a (2) tulajdonság.
Figyelemre méltó az a tény, hogy (1) és (2) inkonzisztens tetszőleges lokális, realisztikus modellel (azaz tetszőleges előre ismert gépezettel)! Tegyük fel, hogy van egy ilyen modellünk. Az E-gépet fel kell készíteni mindegyik lehetséges A, B vagy C mérésre. Vegyük észre, hogy ha csak valószínűségi válasz adására volna felkészítve, akkor a P-gép nem tudna biztosan ellentétes választ adni az A’, B’ vagy C’ mérésnél, amit (1) megkövetel. Mindkét gépben határozottan előre meg kell lennie a válasznak mindhárom lehetséges mérésre. Tegyük fel például, hogy az A, B, C mérésekre e válaszok rendre IGEN, IGEN, IGEN; a jobb oldali részecske ekkor készen kell álljon, hogy NEM, NEM, NEM válaszokat adjon a megfelelő három jobb oldali állásban. Ha az elkészített válaszok a bal oldalon IGEN, IGEN, NEM, akkor a jobb oldali válaszok NEM, NEM, IGEN kell legyenek. Minden más eset lényegében hasonló ezekhez. Nézzük most, összeférhet-e ez (2)-vel. Az IGEN, IGEN, IGEN / NEM, NEM, NEM kiosztások nem ígérnek sokat, mert a lehetséges A/A’, A/B’, A/C’, B/A’ stb. párosításokban ekkor 9 esetben kapunk ellentétet, 0 esetben egyezést. Mi a helyzet az IGEN, IGEN, NEM / NEM, NEM, IGEN és a hasonló típusú esetekkel? Ezek 5 esetben adnak ellentétet, 4 esetben egyezést. (Ellenőrzésképpen számoljuk meg: I/N, I/N, I/I, I/N, I/N, I/I, N/N, N/N, N/I, öt ellentétes, négy egyező.) Ez jóval közelebb áll ahhoz, ami (2)-höz kell, de nem elég jó, mert egyenlő számú egyezés és nem egyezés szükséges! Minden más (1)-gyel összhangban lévő kiosztáspár megint 5 – 4-et adna (kivétel a NEM, NEM, NEM / IGEN, IGEN, IGEN, amely rosszabb, megint 9 – 0-át ad). Nincs olyan előkészített válaszsorozat, amely képes megadni a kvantummechanikai valószínűségeket. A lokális, realisztikus modellek ki vannak zárva!131
Kísérletek fotonokkal: egy probléma a relativitással kapcsolatban?
Meg kell kérdeznünk, hogy megerősítették-e tényleges kísérletek ezeket a meglepő kvantumos várakozásokat. Az itt leírt pontos kísérlet hipotetikus, ténylegesen nem végezték el, de hasonlóakat igen, nem feles spinű, tömeges részecskék spinjét, hanem fotonpárok polarizációját használva. Ettől a különbségtől eltekintve a kísérletek lényegében azonosak az előbb leírtakkal – csak a szóban forgó szögek feleakkorák, mint a feles spinű részecskéknél (mert a fotonok nem feles, hanem egyes spinűek). Fotonpárok polarizációit mérték változatos, különböző iránykombinációkban, és az eredmények teljes egyezést mutatnak a kvantumelmélet jóslataival, és összeférhetetlenek tetszőleges, lokális, realisztikus modellel!
Az eddig kapott legpontosabb és legmeggyőzőbb kísérleti eredményt Alain Aspect és párizsi munkatársai (1986) mutathatják fel.132 Aspect kísérleteinek van egy másik érdekes vonásuk. A „döntést”, hogy milyen módon mérik a fotonok polarizációját, csak akkor hozták meg, amikor a fotonok már javában repültek. Ezért ha azt gondoljuk, hogy valamilyen nemlokális „hatás” megy az egyik fotondetektorból az ellenkező oldalon lévő fotonhoz, jelezve az irányt, amelyben a közeledő foton polarizációját mérni szándékozzuk, akkor látjuk, hogy ennek a „hatásnak” a fénynél gyorsabban kell terjednie! A kvantumvilág bármilyen realisztikus leírása, amely a tényekkel összhangban van, láthatóan akauzális kell legyen olyan értelemben, hogy a hatásoknak a fénynél gyorsabban kell terjedniük!
Az előző fejezetben azonban láttuk, hogy amennyiben a relativitáselmélet igaz, a fénynél gyorsabb jelek küldése abszurditásokhoz vezet (és összeütközéshez „szabadakarat”-érzésünkkel stb., vö. 5. fejezet). Ez biztosan igaz, de a nemlokális „hatásokat”, amelyek az EPR-típusú kísérletekben fellépnek, nem lehet üzenetek küldésére használni – mert éppen olyan abszurditásokhoz vezetnének. [Ennek részletes bemutatását Ghirardi, Rimini és Weber (1980) végezte el.] Nincs értelme azt mondani, hogy egy foton „vagy függőleges, vagy vízszintes irányban” polarizált (és nem mondjuk „vagy 60°-os vagy 150°-os szögben”), amíg nincs információnk arról, hogy melyik valósult meg ténylegesen a két lehetőség közül. Az „információ” első része (azaz az alternatív polarizációs irányok) érkezik meg gyorsabban, mint a fény („pillanatszerűen”), míg az, hogy a két irány közül melyikben van ténylegesen polarizálva, lassabban, egy közönséges jel útján érkezik, amely közli az első polarizációs mérés eredményét.
Noha az EPR-típusú kísérletek az üzenetküldés közönséges értelmezésében nem mondanak ellent a relativitáselmélet kauzalitásának, a „fizikai valóságról” alkotott képünk határozott ellentmondásban áll a relativitás szellemével. Nézzük meg, hogyan viszonyul az állapotvektor valós szemlélete az előző (fotonokkal végzett) EPR-típusú kísérlethez. Amikor a két foton kifelé mozog, az állapotvektor a fotonpárt írja le mint egyetlen egységet. Önmagában egyik fotonnak sincs objektív állapota: a kvantumállapot csak a kettőre együtt alkalmazható. Egyik fotonnak sincs önmagában polarizációs iránya, a polarizáció a két foton együttes, kombinált tulajdonsága. Amikor az egyik foton polarizációját mérjük, az állapotvektor úgy ugrik, hogy a nem mért fotonnak most már van határozott polarizációja. Amikor ezt követően megmérjük ennek a fotonnak a polarizációját, akkor polarizációs állapotára a valószínűségi értékeket alkalmazva helyesen megkapjuk a szokásos kvantumos szabályokat. A helyzetnek ilyen szemlélete a helyes válaszokat adja; valójában rendesen így alkalmazzuk a kvantummechanikát. De e szemlélet lényegesen nemrelativisztikus. A két polarizációs mérés ugyanis térszerűen elválasztott, ami azt jelenti, hogy mindkettő a másik fénykúpján kívül fekszik, mint az R és Q pontok az 5.21. ábrán. A kérdés, hogy a két mérés közül melyik történik meg először, fizikailag nem értelmes, a válasz a „megfigyelő” mozgásállapotától függ (lásd 6.32. ábra). Ha a „megfigyelő” elég gyorsan mozog jobbra, akkor szerinte a jobb oldali mérés az első, ha balra mozog elég gyorsan, akkor a bal oldali! Ám a fizikai valóság teljesen eltérő képeit kapjuk, ha egyszer a jobb oldali, másszor a bal oldali mérést tekintjük elsőnek! (Más-más mérés okozza a nemlokális „ugrást”.) Lényeges ellentmondás van a fizikai valóságról alkotott téridőképünk – még ha az a helyes módon nemlokális kvantummechanikai kép is – és a speciális relativitáselmélet között! Ez igazi rejtély, amelyet a „kvantumrealisták” nem voltak képesek megfelelően megoldani (vö. Aharonov és Albert 1981). Később erre vissza kell majd térnem.
Schrödinger-egyenlet, Dirac-egyenlet
Korábban e fejezetben utaltam a Schrödinger-egyenletre, amely tökéletesen jól meghatározott, determinisztikus egyenlet, sok tekintetben nagyon hasonló a klasszikus fizika egyenleteihez. A szabályok azt mondják, hogy amíg egy kvantumrendszeren nem végzünk „mérést” (vagy „megfigyelést”), addig a Schrödinger-egyenletnek érvényesnek kell lennie. Az Olvasó most megismerkedhet az egyenlet alakjával:
Emlékezzünk vissza, hogy ħ a Planck-állandó Dirac-féle változata (h/2π),
, és a ∂/∂t operátor (parciális differenciálás az idő szerint) hatása |ψ〉-re |ψ〉 időbeli változási sebességét jelenti. A Schrödinger-egyenlet azt állítja, hogy H|ψ〉 leírja |ψ〉 időbeli fejlődését.
De micsoda a H? A Hamilton-függvény, amit az előző fejezetben megismertünk, de egy alapvető különbséggel! Idézzük fel, hogy a klasszikus Hamilton-függvény a teljes energia kifejezése a rendszerben lévő összes fizikai objektum különböző q, hely- és pi impulzuskoordinátáival. A kvantumos Hamilton-függvényt úgy kapjuk, hogy vesszük ugyanazt a kifejezést, de mindegyik pi impulzust a „qi szerinti parciális differenciálás” differenciáloperátorának egy többszörösével helyettesítjük. Konkrétan szólva pi-t –iħ∂/∂qi-vel helyettesítjük. A kvantumos H Hamilton-függvényünk így valamilyen (gyakran bonyolult) matematikai operáció lesz, differenciálásokkal, szorzásokkal stb. – és nem puszta szám! Ez hókuszpókusznak látszik! Ám nem csupán matematikai bűvészkedés; igazi varázslat, amely működik! (Van egy kis „művészet” abban, ahogy ezzel az eljárással egy klasszikus Hamilton-függvényből kvantumosat hozunk létre, de szokatlanságát tekintve figyelemre méltó, mennyire kevéssé számítanak az eljárásban benne rejlő bizonytalanságok.)
A Schrödinger-egyenlet fontos tulajdonsága, hogy lineáris (akármilyen is H), azaz ha |ψ〉 és |φ〉 kielégítik az egyenletet, akkor kielégíti |ψ〉 + |φ〉 is – sőt tetszőleges w|ψ〉 + z|φ〉 kombináció is, ahol w és z rögzített komplex számok. Így a komplex lineáris szuperpozíciót a Schrödinger-egyenlet tetszés szerinti ideig megőrzi. Két lehetséges állapot (komplex) lineáris szuperpozíciója csupán U hatására nem válhat „szuperponálatlanná”! Ezért van szükség R hatására, mint U-tól különálló eljárásra, hogy végül csak egy alternatíva maradjon meg.
Hasonlóan a klasszikus fizika Hamilton-formalizmusához, a Schrödinger-egyenlet nem annyira egy speciális egyenlet, hanem általános keret a kvantummechanikai egyenletek számára. Ha egyszer a megfelelő kvantumos Hamilton-függvényt megkaptuk, akkor az állapot időfejlődése a Schrödinger-egyenlet szerint eléggé úgy megy, mintha |ψ〉 valamely klasszikus egyenletnek, pl. a Maxwell-féléknek engedelmeskedő klasszikus mező volna. Ha |ψ〉 egyetlen foton állapotát írja le, akkor a Schrödinger-egyenlet történetesen a Maxwell-egyenletekké válik! Az egyetlen fotonra vonatkozó egyenlet pontosan ugyanaz, mint a teljes elektromágneses mezőre vonatkozó egyenlet.133 Ez a körülmény felelős az egyes fotonok hullámszerű viselkedéséért és polarizációjáért, amiről korábban már volt szó. Egy másik példa: ha |ψ〉 egyetlen elektron állapotát írja le, akkor a Schrödinger-egyenlet Diracnak az elektronra felírt nevezetes hullámegyenletévé válik – amelynek 1928-as felfedezéséhez Dirac különleges eredetiségére és sajátos meglátására volt szükség.
Diracnak az elektronra vonatkozó egyenletét a Maxwell- és Einstein-egyenletek mellett a fizika Nagy Mezőegyenletei közé sorolhatjuk. Hogy az Olvasó megfelelő benyomásokat szerezhessen róla, ahhoz olyan matematikai fogalmakat kellene bevezetnem, amelyek túlságosan zavaróak volnának. Elég az hozzá, hogy a Dirac-egyenletben |ψ〉-nek megvan az a korábban említett különös „fermionos” tulajdonsága, hogy 360°-os forgatásra |ψ〉 → –|ψ〉. A Dirac- és Maxwell-egyenletek együtt képezik a kvantumelektrodinamika alapvető alkotórészeit, ez a legsikeresebb a kvantum-mezőelméletek közül. Ezt tekintjük át most röviden.
133 Van azonban egy fontos különbség a megoldás megengedett típusában. A klasszikus Maxwell-mezők szükségszerűen valósak, míg a fotonállapotok komplexek. Van még egy ún. „pozitív frekvenciás” feltétel is, amelyet a fotonállapotnak ki kell elégítenie.
Kvantum-mezőelmélet
A „kvantum-mezőelmélet” néven ismert tárgykör a speciális relativitáselmélet és a kvantummechanika elveinek egyesítéséből nőtt ki. A szokásos (azaz nemrelativisztikus) kvantummechanikától abban különbözik, hogy bármelyik típusú részecske számának nem kell állandónak lennie. Mindegyiknek megvan az antirészecskéje (olykor, például a foton esetében, azonos az eredeti részecskével). Egy tömeges részecske és antirészecskéje egymást megsemmisítve energiává tud szétsugározni, és elegendő energia létre tud hozni egy ilyen párt. A részecskék száma még meghatározott sem kell legyen; megengedett az olyan állapotok lineáris szuperpozíciója, amelyekben a részecskék száma különböző. A legfontosabb kvantum-mezőelmélet a „kvantumelektrodinamika” – alapvetően az elektronok és fotonok elmélete. Ez az elmélet jóslatainak pontosságáról nevezetes (ilyen például az elektron mágneses momentumának pontos értéke, amelyre az előző fejezetben utaltam). Ám az elmélet meglehetősen rendetlen – és nem teljesen következetes –, mert kezdetben értelmetlen „végtelen” válaszokat ad. Ezeket egy „renormalizáció” nevű eljárással el kell tüntetni. Nem minden kvantum-mezőelmélet renormálható, és a számolás azokban is nehéz, amelyek ilyenek.
A kvantum-mezőelméletek egy népszerű megközelítése a „pályaintegrál”-módszer, amelyben nem különböző részecskeállapotokból képeznek kvantumos lineáris szuperpozíciókat (mint a közönséges hullámfüggvények), hanem a fizikai viselkedés teljes téridő történeteiből (egy népszerű tárgyalását lásd Feynman 1985). Ám e megközelítés további sajátos végteleneket tartalmaz, és ezeket csak különféle „matematikai trükkök” bevezetésével lehet értelmessé tenni. A kvantum-mezőelmélet kétségtelen ereje és (abban a néhány esetben, ahol a számítások teljesen végrehajthatók) meggyőző pontossága ellenére az embernek az az érzése marad, hogy mélyebb megértésre van szükség, mielőtt biztosak lehetnénk a „fizikai valóság képében”, amelyhez elvezetni látszik.134
Szeretném világossá tenni, hogy a kvantumelméletnek és a speciális relativitáselméletnek a kvantum-mezőelmélet által megvalósított összhangja csak részleges – csak U-ra vonatkozik – és meglehetősen formális matematikai természetű. Az R-rel bekövetkező „kvantumugrások” következetes relativisztikus értelmezésének nehézségét, amelyet az EPR-típusú kísérletek vetettek fel, a kvantum-mezőelmélet nem is érinti. Nincs következetes vagy elhihető kvantum-mezőelmélete a gravitációnak sem. A 8. fejezetben azt fogom sugallni, hogy ezek a dolgok nem lehetnek egymástól függetlenek.
134 A kvantum-mezőelméletben, úgy látszik, felmerülhet a nemkiszámíthatóság kérdése (vö. Komar 1964).
Ám e megközelítés további sajátos végteleneket tartalmaz, és ezeket csak különféle „matematikai trükkök” bevezetésével lehet értelmessé tenni.
Ocham borotvája
Az R-rel bekövetkező „kvantumugrások” következetes relativisztikus értelmezésének nehézségét, amelyet az EPR-típusú kísérletek vetettek fel, a kvantum-mezőelmélet nem is érinti. Nincs következetes vagy elhihető kvantum-mezőelmélete a gravitációnak sem. A 8. fejezetben azt fogom sugallni, hogy ezek a dolgok nem lehetnek egymástól függetlenek.
Amennyiben valódi létezők, mint a fizikai világ "mélyrétegei", akkor valóban nem lehetnek függetlenek egymástól.
Schrödinger macskája
Térjünk vissza végül egy olyan kérdésre, amely a leírás kezdetétől fogva kísért bennünket. Miért nem látjuk a klasszikus méretű objektumok kvantumos lineáris szuperpozícióit, például a krikettlabdát egyszerre két helyen? Mi az, ami az atomok bizonyos elrendezéseit „mérőeszközzé” teszi, és ekkor U átadja helyét az R eljárásnak? Minden mérőberendezés nyilván maga is része a fizikai világnak, ugyanazokból a kvantummechanikai alkotórészekből épül fel, amelyek viselkedésének feltárására esetleg tervezték. Miért ne kezeljük a mérőberendezést együtt a vizsgált fizikai rendszerrel, mint egy összetett kvantumos rendszert? Akkor nincs szó semmiféle titokzatos „külső” mérésről. Az együttes rendszernek U szerint kellene fejlődnie. Ezt teszi? U hatása az együttes rendszerre tökéletesen determinisztikus, a „mérésben” vagy „megfigyelésben”, amelyet az összetett rendszer magán hajt végre, nincs helye R típusú valószínűségi bizonytalanságoknak! Látható ellentmondás feszül itt, amely különösen szemléletesen jelentkezik Erwin Schrödinger híres gondolatkísérletében (1935): ez a Schrödinger macskája paradoxon.
Képzeljünk el egy tökéletesen elkészített, lepecsételt tartályt, amelynek falain keresztül se befelé, se kifelé nem mehet át semmiféle fizikai hatás. Gondoljuk azt, hogy a tartályban van egy macska meg egy műszer, amelyet egy kvantumos esemény vezérelhet. Ha ez az esemény bekövetkezik, akkor a műszer összetör egy ciánt tartalmazó ampullát, és a macska elpusztul. Ha az esemény nem következik be, akkor a macska él tovább. A kvantumos esemény Schrödinger eredeti változatában egy radioaktív atom bomlása volt. Hadd módosítsam ezt kissé úgy, hogy az esemény egy fotocella jelzése legyen egy foton beérkezésére. A fotont egy fényforrás bocsátja ki előre meghatározott állapotban, majd egy félig ezüstözött tükör kerül az útjába (lásd 6.33. ábra). A tükör két részre hasítja a foton hullámfüggvényét, az egyik visszaverődik, a másik átmegy a tükrön. A foton hullámfüggvényének visszavert részét fókuszáljuk a fotocellára, tehát ha ez jelzi a fotont, akkor az visszaverődött. Ebben az esetben a cián kiszabadul, a macska elpusztul. Ha a fotocella nem jelez, akkor a foton átment a félig ezüstözött tükrön a mögötte lévő falra, a macska megmenekül.
A történet leírása valóban ez volna a tartályon belül lévő megfigyelő (némileg hazárd) nézőpontjából. (Jó lesz, ha ellátjuk őt megfelelő védőruhával!) A foton vagy visszaverődött, mert emberünk „megfigyelte”, hogy a fotocella jelzett, és a macska elpusztult, vagy átjutott a tükrön, mert „megfigyelte”, hogy a fotocella nem jelzett, és a macska él. Vagy egyik, vagy másik ténylegesen bekövetkezik: R működésbe lép, és mindkét lehetőség valószínűsége 50% (mert a tükör félig ezüstözött). Nézzük most az egészet a tartályon kívül lévő fizikus szemével. Úgy vehetjük, hogy lezárás előtt „ismerte” a tartály tartalmának kezdeti állapotvektorát. (Nem gondolom, hogy gyakorlatilag ismerhető, ám a kvantumelméletben semmi olyan nincsen, ami azt mondaná, hogy nem ismerheti elvileg.) A külső megfigyelő szerint „mérés” ténylegesen nem történt, ezért az állapotvektornak teljesen U szerint kellett fejlődnie. A foton előre meghatározott állapotában került ki a forrásból – ebben mindkét megfigyelő egyetért –, hullámfüggvénye két részre hasad, mondjuk
az amplitúdója mindkét lehetőségnek (az abszolútérték-négyzetek így valóban 1/2 valószínűségeket adnak). Minthogy a külső megfigyelő a tartály teljes tartalmát egyetlen kvantumrendszerként kezeli, a lehetőségek lineáris szuperpozíciójának egészen a macska skálájáig fenn kell maradnia.
az amplitúdója annak, hogy a fotocella jelez, 1 /
annak, hogy nem jelez. Az állapotban mindkét lehetőségnek jelen kell lennie, mint egyformán súlyozott részei egy kvantumos lineáris szuperpozíciónak. A külső megfigyelő szerint a macska a halott és élő állapot lineáris szuperpozíciójában van!
Hisszük-e valóban, hogy ez a helyzet? Schrödinger világosan kifejtette, hogy ő nem hiszi. Úgy érvelt, hogy a kvantummechanika U szabálya nem lehet alkalmazható olyan nagy vagy bonyolult valamire, mint egy macska. Közben valahol csődöt kell mondjon az egyenlet. Schrödingernek természetesen joga volt, hogy saját egyenletéről így vélekedjék, de nekünk, többieknek ez az előjog nem adott. Nagyon sok (valószínűleg a legtöbb) fizikus kitartana amellett, hogy a dolgok éppen ellenkezően állnak: ma már oly sok kísérleti bizonyíték szól U mellett – ellene pedig egy sem –, hogy nincs jogunk feladni a fejlődés e típusát még egy macska skáláján sem. Ha ezt elfogadjuk, akkor, úgy látszik, a fizikai valóságnak egy nagyon szubjektív szemléletéhez jutunk. A külső megfigyelő számára a macska valóban az élő és holt állapot lineáris kombinációjában van, és csak amikor a tartályt végül felnyitjuk, állapotvektora akkor ugrik be egyikbe vagy másikba. Másrészt viszont egy, a tartály belsejében lévő (megfelelően védett) megfigyelő szerint a macska állapotvektora sokkal korábban ugrott, és a külső megfigyelő
lineáris kombinációjának nincs jelentősége. Úgy látszik, hogy az állapotvektor végül is „a fejünkben” van!
Elfogadhatjuk-e az állapotvektor ilyen szubjektív szemléletét? Tegyük fel, hogy a külső megfigyelő csinált valami sokkal finomabbat, nem csupán „nézett” befelé a tartályba. Tegyük fel, hogy ismerve a tartály belsejének kezdeti állapotát, a rendelkezésére álló hatalmas számítókapacitást és a Schrödinger-egyenletet használva először kiszámítja, milyen kell legyen a tényleges állapot, és megkapja a („helyes”) |ψ〉 választ (ahol |ψ〉 valóban tartalmazza egy halott macska és egy élő macska előbbi lineáris szuperpozícióját). Tegyük fel, hogy ezután elvégzi azt a speciális kísérletet, amely az igazi |ψ〉 állapotot megkülönbözteti tetszőleges |ψ〉-re ortogonális állapottól. (Mint azt korábban leírtam, a kvantummechanika szabályai szerint elvileg el tud végezni ilyen kísérletet, noha ez a gyakorlatban rettenetesen nehéz volna.) A két lehetőség, „igen, a |ψ〉 állapotban van” és „nem, ortogonális |ψ〉-re” valószínűsége 100% és 0% volna. Speciálisan zérus a valószínűsége a ∣χ〉 = ∣halott〉 – ∣élő〉 állapotnak, amely ortogonális |ψ〉-re. ∣χ〉 lehetetlensége csak azért lehet a kísérlet eredménye, mert a két alternatíva együtt él, és interferál egymással.
Ugyanez igaz volna, ha a foton úthosszát (vagy az ezüstözés mértékét) egy kicsit módosítanánk úgy, hogy a ∣halott〉 + ∣élő〉 állapot helyett más kombináció, mondjuk a ∣halott〉 – i∣élő〉 stb. valósulna meg. E különböző kombinációk mind eltérő kísérleti következményeket vonzanak – elvileg! Így nem is „csupán” a halál és élet egyfajta együttléte bánthatja szegény macskánkat. Minden különböző komplex kombináció megengedett, és elvileg mind megkülönböztethető egymástól! Azonban a tartályon belül lévő megfigyelő számára e kombinációk mind lényegtelennek látszanak. A macska vagy élő, vagy holt. Hogyan érthetjük meg ezt a fajta ellentmondást? Felvázolok egy pár különböző nézőpontot, amelyek ennek (és rokon kérdéseknek) a megválaszolására születtek – noha kétségtelenül nem leszek igazságos mindegyikkel!
E különböző kombinációk mind eltérő kísérleti következményeket vonzanak – elvileg! Így nem is „csupán” a halál és élet egyfajta együttléte bánthatja szegény macskánkat. Minden különböző komplex kombináció megengedett, és elvileg mind megkülönböztethető egymástól! Azonban a tartályon belül lévő megfigyelő számára e kombinációk mind lényegtelennek látszanak. A macska vagy élő, vagy holt. Hogyan érthetjük meg ezt a fajta ellentmondást?
- kérdi Penrose, és ő hiszi, hogy fel lehet oldani, hiszi hogy a világ nem képzetes, bennünk élő valami, nem látszatvilág.
- Ez is szellemes, ahogy Schrödinger "nem-hitéről" ír:
Hisszük-e valóban, hogy ez a helyzet? Schrödinger világosan kifejtette, hogy ő nem hiszi. Úgy érvelt, hogy a kvantummechanika U szabálya nem lehet alkalmazható olyan nagy vagy bonyolult valamire, mint egy macska. Közben valahol csődöt kell mondjon az egyenlet. Schrödingernek természetesen joga volt, hogy saját egyenletéről így vélekedjék, de nekünk, többieknek ez az előjog nem adott.
Különféle álláspontok a létező kvantumelméletben
Először is vannak nyilvánvaló nehézségek az olyan kísérlettel, amely a |ψ〉 állapotot megkülönbözteti tetszőleges, |ψ〉-re ortogonális állapottól. Nem kétséges, hogy a külső megfigyelő számára egy ilyen kísérlet gyakorlatilag lehetetlen. Ismerni kellene ugyanis a tartály teljes tartalmának (a bent lévő megfigyelőnek is) pontos állapotvektorát, mielőtt elkezdhetné számítani, mi volna |ψ〉 a későbbi időpontokban! Elvárjuk azonban, hogy e kísérlet ne csak a gyakorlatban, elvileg is lehetetlen legyen, mert másképpen nem volna jogunk az „∣élő〉” vagy „∣halott〉” állapotok egyikét eltávolítani a fizikai valóságból. A baj az, hogy a kvantumelmélet jelenlegi formájában nem húz határozott vonalat a „lehetséges” és „lehetetlen” kísérletek között. Pedig talán van ilyen világos megkülönböztetés. Az elmélet mai állásában nem ad rá módot. Bevezetése megváltoztatná a kvantumelméletet.
Másodszor van az a nem szokatlan nézőpont, hogy a nehézségek eltűnnének, ha a környezetet megfelelően figyelembe tudnánk venni. Gyakorlatilag lehetetlen a tartály tartalmát teljesen izolálni a külső világtól. Amint a külső környezet hozzáadódik a tartály belsejének állapotához, a külső megfigyelő nem tekintheti a tartály tartalmát egyetlen állapotvektorral megadottnak. Még saját állapota is bonyolult módon korrelációba kerül vele. Mi több, hatalmas számú különböző részecske kapcsolódik be elkerülhetetlenül a lehetséges lineáris kombinációk hatásait mind távolabbra kiterjesztve a világegyetembe, óriási számú szabadsági fokra. Nincs gyakorlati lehetőség arra, hogy (mondjuk alkalmas interferenciajelenségek megfigyelésével) megkülönböztessük e komplex lineáris szuperpozíciókat a csupán valószínűségi súlyozású alternatíváktól. Ez még nem is csak a tartalom izolálásának kérdése. Maga a macska is hatalmas számú részecskét tartalmaz. Ezért a halott és élő macska komplex lineáris szuperpozícióját úgy kezelhetjük, mintha csak egyszerű valószínűségi keverék volna. Ám én ezt egyáltalán nem találom kielégítőnek. Mint az előző szemléletnél, most is megkérdezhetjük, „hivatalosan” melyik szinten válnak „lehetetlenné” az interferenciajelenségek – mikor jelenthetjük ki a komplex szuperpozíció amplitúdóinak abszolútérték-négyzeteiről, hogy azok a „halott” és „élő” valószínűségi súlyai. Még ha a világ „valósága” bizonyos értelemben „ténylegesen” valós szám valószínűségi súlyozássá is válik, hogyan oldódik fel az állapot pont az egyik vagy másik alternatívában? Nem látom, hogyan képes a valóság önmagát két alternatíva komplex (vagy valós) lineáris szuperpozíciójából áttranszformálni egyikbe vagy másikba csupán az U fejlődés alapján. Úgy látszik, hogy a világ egy szubjektív szemléletéhez kerültünk vissza!
Egyesek olykor azt vallják, hogy a bonyolult rendszereket valójában nem „állapotokkal” kell leírni, hanem ezek egy általánosításával, amelyet sűrűségmátrixnak neveznek (Neumann 1955). Ez magában foglalja mind a klasszikus valószínűségeket, mind a kvantumamplitúdókat. A sűrűségmátrixok hasznosak, de önmagukban nem oldják meg a kvantumos mérés mély problémáit.
Lehet próbálkozni azzal, hogy a tényleges fejlődés a determinisztikus U, ám a valószínűségek abból a bizonytalanságból erednek, hogy az együttes rendszer kvantumállapotát nem ismerjük pontosan. Ez a valószínűségek eredetének egy nagyon „klasszikus” szemlélete volna – hogy teljesen a kezdeti állapot bizonytalanságaiból származnak. Elképzelhetjük, hogy parányi különbségek a kezdeti állapotban hatalmas különbségeket eredményezhetnének a fejlődés során, hasonlóan a klasszikus rendszereknél előfordulható „káoszhoz” (pl. időjárás-előrejelzés; vö. 5. fejezet). Azonban az ilyen „kaotikus” jelenségek nem lehetnek U eredményei, mert az lineáris: a felesleges lineáris szuperpozíciók U hatására soha nem tűnnek el! Hogy egy ilyen szuperpozíció feloldódjon egyik vagy másik alternatívában, ahhoz valami nemlineáris szükséges, U önmagában nem elégséges.
Egy másik nézőpont számára rögzíthetjük azt a tényt, hogy a Schrödinger macskája kísérletben az egyetlen nyilvánvaló ellentmondás a megfigyeléssel azért látszik fellépni, mert tudatos megfigyelők vannak, egy (vagy kettő) a tartályon belül, egy kívül. A komplex kvantumos lineáris szuperpozíciók törvényei esetleg nem érvényesek a tudatosságra! E nézőpont egy durva matematikai modelljét Wigner Jenő (1961) állította fel. Azt sugallta, hogy a Schrödinger-egyenlet linearitása tudatos (vagy csupán „élő”) lényekre elromolhat, valamilyen nemlineáris eljárással kell helyettesíteni, amely szerint megjelenne egyik vagy másik alternatíva. Az Olvasó úgy érezheti, hogy mert keresem a kvantumos jelenségek szerepét tudatos gondolkodásunkban – és valóban keresem –, ezért e nézőpontot rokonszenves lehetőségnek kell találnom. Ám egyáltalán nem vagyok boldog tőle. Úgy látom, hogy a világ „valóságának” egy nagyon féloldalas és zavaros szemléletéhez vezet. A világegyetem azon sarkai, ahol tudatosság van jelen, nagyon kisszámúak lehetnek, és nagyon szétszórtak. E nézet szerint a komplex kvantum lineáris szuperpozíciók csak ezekben a sarkokban oldódnának fel a tényleges alternatívák valamelyikében. Lehet, hogy számunkra ezek a sarkok ugyanúgy néznének ki, mint a világegyetem maradék része, mert akármire is néznénk rá (vagy figyelnénk meg másképpen), éppen tudatos megfigyelésünk következtében az „alternatívákban oldódna fel”, akár tette ezt azelőtt, akár nem. Ám ez a nagy féloldalasság nagyon zavaró képet adhat a világ valóságosságáról, és a magam részéről igencsak vonakodnék elfogadni.
Van egy ehhez némileg kapcsolódó nézőpont, az ún. részt vevő világegyetem (John A. Wheeler 1983 javaslata), amely (másféle) szélsőségig viszi a tudatosság szerepét. A tudatos élet e világ bolygóin a változatos időpontokban végbemenő, megfelelő mutációk következtében fejlődik. Ezek feltehetően kvantumos események, tehát mindaddig csak lineárisan szuperponált formában léteznek, amíg végül egy tudatos lény kifejlődéséhez vezetnek – akinek a létezése maga azon múlik, hogy az összes helyes mutáció „ténylegesen” megtörténik-e! Saját jelenlétünk az, ami e nézet szerint múltunkat létezéssé varázsolja. A körbezáruló és paradox kép vonzó egyesek számára, ám én különösen aggasztónak és valójában alig hihetőnek találom.
Egy másik, a maga módján logikus, de nem kevésbé furcsa képet nyújtó nézőpont a sokvilág-elmélet, amelyet először Hugh Everett (1957) vetett fel nyilvánosan. Eszerint R soha nem történik meg. A valóságosnak tekintett állapotvektor teljes fejlődését mindig a determinisztikus U eljárás irányítja. Ebből az következik, hogy Schrödinger szegény macskája, és vele a tartályban lévő védett megfigyelő, valóban komplex lineáris kombinációban kell létezzen, a macska élet és halál szuperpozíciójában. Azonban a halott állapot korrelált a belső megfigyelő tudatának egyik állapotával, az élő egy másikkal (és feltehetően részben a macska tudatával – és végül a külső megfigyelőével is, amikor a tartalom tudomására jut). Mindegyik megfigyelő tudata „felhasad”, így két példányban létezik, a példányok mást és mást tapasztalnak (azaz egyikük halott macskát lát, a másik élőt). Valójában nem csupán egy megfigyelő, de az általa lakott egész világegyetem ketté- (vagy több részre) hasad a világon végzett minden „mérés” során. E felhasadás újból és újból bekövetkezik – nemcsak a megfigyelők által végzett „mérések”, hanem általában a kvantumos események makroszkopikussá nagyítása miatt –, így ezek a világegyetem-„ágak” vadul szaporodnak. Valójában minden alternatív lehetőség egy hatalmas szuperpozícióban él együtt. Aligha ez a leggazdaságosabb nézőpont, de ellenvetéseim nem a gazdaságosság hiányára vonatkoznak. Nem látom, hogy egy tudatos lény miért csak egy lineáris szuperpozíció „egy” alternatívájának lehet tudatában. Mi van a tudatosságban, ami megköveteli, hogy valaki nem lehet „tudatában” a halott és élő macska gyötrő lineáris kombinációjának? Úgy látom, hogy a tudatosság elméletére volna szükség, mielőtt a sokvilág-elméletet összevethetnénk azzal, amit valóban megfigyelünk. Nem látom, mi a kapcsolata ez utóbbival a világegyetem „igazi” (objektív) állapotvektorának. Egyesek szerint e képben valamilyen értelemben ténylegesen levezethető R „illúziója”, de nem hiszem, hogy ez igaz. A legkevesebb az, hogy a dolog működéséhez további kellékekre van szükség. Én úgy látom, hogy a sokvilág-kép csak megsokszorozza a problémákat, anélkül, hogy érintené a kvantumos mérés igazi rejtelmeit (lásd DeWitt és Graham 1973).
a./Penrose hite:
Elvárjuk azonban, hogy e kísérlet ne csak a gyakorlatban, elvileg is lehetetlen legyen, mert másképpen nem volna jogunk az „∣élő〉” vagy „∣halott〉” állapotok egyikét eltávolítani a fizikai valóságból. A baj az, hogy a kvantumelmélet jelenlegi formájában nem húz határozott vonalat a „lehetséges” és „lehetetlen” kísérletek között. Pedig talán van ilyen világos megkülönböztetés. Az elmélet mai állásában nem ad rá módot. Bevezetése megváltoztatná a kvantumelméletet.
1./Nem szeretné, ha a világot csak szubjektíven szemlélhetnénk, Penrose viszolyog a "szubjektív idealizmustól". Azt sem szíveli, ha a tudós, jelen esetben a kvantumfizikus, megriad a kísérletekből leszűrhető ellentmondásoktól és "vadabbnál-vadabb" további feltételezésekbe bonyolódik ahelyett, hogy abból indulna ki, amit már biztosan tudunk és abból építkezne tovább. Téglát a téglára, mint ama asssissi tette.:
Maga a macska is hatalmas számú részecskét tartalmaz. Ezért a halott és élő macska komplex lineáris szuperpozícióját úgy kezelhetjük, mintha csak egyszerű valószínűségi keverék volna. Ám én ezt egyáltalán nem találom kielégítőnek. Mint az előző szemléletnél, most is megkérdezhetjük, „hivatalosan” melyik szinten válnak „lehetetlenné” az interferenciajelenségek – mikor jelenthetjük ki a komplex szuperpozíció amplitúdóinak abszolútérték-négyzeteiről, hogy azok a „halott” és „élő” valószínűségi súlyai. Még ha a világ „valósága” bizonyos értelemben „ténylegesen” valós szám valószínűségi súlyozássá is válik, hogyan oldódik fel az állapot pont az egyik vagy másik alternatívában? Nem látom, hogyan képes a valóság önmagát két alternatíva komplex (vagy valós) lineáris szuperpozíciójából áttranszformálni egyikbe vagy másikba csupán az U fejlődés alapján. Úgy látszik, hogy a világ egy szubjektív szemléletéhez kerültünk vissza!
2./Neumann "sűrűségmátrix"-át felhasználja Penrose, de ez még indig nem oldja fel az ellentmondást-mondja.
3./ A "káosz" létrejöttének oka nem lehet a linearitás (egy egyenesvonalú fejlődést leíró függvény ilyet nem tartalmazhat.- írja:
Hogy egy ilyen szuperpozíció feloldódjon egyik vagy másik alternatívában, ahhoz valami nemlineáris szükséges, U önmagában nem elégséges.
4/ egy másik nézőpont Wigner Jenőé, na ő is kap kritikát Penrose-tól rendesen:
A komplex kvantumos lineáris szuperpozíciók törvényei esetleg nem érvényesek a tudatosságra! E nézőpont egy durva matematikai modelljét Wigner Jenő (1961) állította fel. Azt sugallta, hogy a Schrödinger-egyenlet linearitása tudatos (vagy csupán „élő”) lényekre elromolhat, valamilyen nemlineáris eljárással kell helyettesíteni, amely szerint megjelenne egyik vagy másik alternatíva. Az Olvasó úgy érezheti, hogy mert keresem a kvantumos jelenségek szerepét tudatos gondolkodásunkban – és valóban keresem –, ezért e nézőpontot rokonszenves lehetőségnek kell találnom. Ám egyáltalán nem vagyok boldog tőle. Úgy látom, hogy a világ „valóságának” egy nagyon féloldalas és zavaros szemléletéhez vezet.
5./Megint mások szerint:
Saját jelenlétünk az, ami e nézet szerint múltunkat létezéssé varázsolja. A körbezáruló és paradox kép vonzó egyesek számára, ám én különösen aggasztónak és valójában alig hihetőnek találom.
6./ Hugh Everett (1957) sokvilág-elmélete sem tetszik neki:
Nem látom, hogy egy tudatos lény miért csak egy lineáris szuperpozíció „egy” alternatívájának lehet tudatában. Mi van a tudatosságban, ami megköveteli, hogy valaki nem lehet „tudatában” a halott és élő macska gyötrő lineáris kombinációjának? Úgy látom, hogy a tudatosság elméletére volna szükség, mielőtt a sokvilág-elméletet összevethetnénk azzal, amit valóban megfigyelünk. Nem látom, mi a kapcsolata ez utóbbival a világegyetem „igazi” (objektív) állapotvektorának. Egyesek szerint e képben valamilyen értelemben ténylegesen levezethető R „illúziója”, de nem hiszem, hogy ez igaz. A legkevesebb az, hogy a dolog működéséhez további kellékekre van szükség. Én úgy látom, hogy a sokvilág-kép csak megsokszorozza a problémákat, anélkül, hogy érintené a kvantumos mérés igazi rejtelmeit
"Rejtelmek ha zengenek," [J.A.]
Mi marad nekünk?
Ezek a rejtélyek ilyen vagy olyan megjelenésben megtalálhatók a kvantummechanika bármelyik értelmezésében, ahogy az elmélet ma áll. Röviden összefoglaljuk, mit mond a szabványos kvantumelmélet arról, hogyan kell leírnunk a világot – különös tekintettel e rejtélyes kérdésekre –, és azután megkérdezzük: merrefelé is megyünk?
Először is emlékezzünk arra, hogy a kvantumelmélet leírásai értelmesen (hasznosan?) csak az úgynevezett kvantumszinten látszanak alkalmazhatónak – a molekulák, atomok vagy szubatomi részecskék szintjén, de nagyobb dimenziókban is, amíg az alternatívák közötti energiakülönbségek nagyon kicsik. Kvantumszinten úgy kell kezelnünk az ilyen „alternatívákat”, mint amelyek komplex számokkal súlyozott szuperpozíciókban együtt élhetnek. A komplex szám súlyokat valószínűségi amplitúdóknak nevezzük. Mindegyik különböző komplex lineáris szuperpozíció különböző kvantumállapotot határoz meg, és tetszőleges kvantumos rendszert ilyen kvantumállapotokkal kell leírnunk. Gyakran semmit nem lehet arról mondani, melyek a kvantumállapotot képező „tényleges” alternatívák, és melyek csupán alternatívák „kombinációi”. Mindenesetre amíg a rendszer a kvantumszinten marad, addig a kvantumállapot tökéletesen determinisztikus módon fejlődik. E determinisztikus fejlődés az U folyamat, amit a fontos Schrödinger-egyenlet irányít.
Amikor a különböző kvantumalternatívák hatásai felnagyítódnak a klasszikus szintre, és a közöttük lévő különbségek elég nagyok ahhoz, hogy közvetlenül észleljük azokat, akkor úgy látszik, hogy az ilyen komplexsúlyozott szuperpozíciók nem élnek tovább. Ehelyett képeznünk kell a komplex amplitúdók abszolútérték-négyzeteit (azaz négyzetes távolságukat a komplex sík kezdőpontjától), és e valós számok jutnak új szerephez mint a szóban forgó alternatívák valószínűségei. A fizikai tapasztalat valóságában csak az egyik alternatíva él tovább, mégpedig az R folyamat szerint (ezt hívják az állapotvektor redukciójának vagy a hullámfüggvény kollapszusának; az U-tól teljesen különbözik). Itt és csak itt léphet be a kvantumelmélet indeterminizmusa.
Komoly érvek szólnak amellett, hogy a kvantumállapot objektív képet nyújt. Ám ez a kép lehet bonyolult, sőt némileg paradox is. Amikor több részecskéről van szó, akkor a kvantumállapotok nagyon bonyolulttá válhatnak (és rendesen „meg is teszik”). Az egyes részecskéknek maguknak ekkor nincsenek „állapotaik”, csak bonyolult „keverékekben” léteznek a többi részecskével együtt, ezek a korrelációk. Amikor egy részecskét „megfigyelünk”, abban az értelemben, hogy kivált valamilyen jelenséget, ami felnagyítódik a klasszikus szintre, akkor R-et kell segítségül hívni – ám ez láthatóan egyidejűleg az összes részecskét befolyásolja, amellyel a kiválasztott részecske korrelált. Az Einstein–Podolsky–Rosen- (EPR-) típusú kísérletek (mint az Aspect-féle is, amelyben egy kvantumos forrás fotonpárokat bocsát ki ellentétes irányban, majd azok polarizációját mérik egymástól függetlenül sok méteres távolságban) világos megfigyelési anyagot szolgáltatnak a kvantumfizika e rejtélyes, de lényeges jelenségéhez: azt, hogy nem lokális (vagyis a fotonok Aspect kísérletében nem kezelhetők különálló, független objektumokként)! Ha úgy tekintjük, hogy R objektív módon működik (és a kvantumállapot objektivitása erre enged következtetni), akkor megsértjük a speciális relativitáselmélet szellemét. Úgy látszik, hogy a (redukción áteső) állapotvektornak nincs objektíven valós téridőleírása, amely összhangban lenne a relativitáselmélet követelményeivel! Azonban a kvantumelmélet megfigyelhető jelenségei nem sértik a relativitáselméletet.
A kvantumelmélet hallgat arról, ténylegesen mikor és miért következik be (vagy látszik bekövetkezni) R? Továbbmenve, önmagában nem magyarázza meg rendesen, miért „látszik” a klasszikus szintű világ klasszikusnak. A „legtöbb” kvantumállapot egyáltalán nem emlékeztet klasszikusra!
Mi marad hát számunkra? Azt hiszem, erősen számításba kell vennünk azt a lehetőséget, hogy amikor makroszkopikus testekre alkalmazzuk, a kvantummechanika egyszerűen rossz – vagy inkább, hogy az U és R törvények csak kitűnő közelítései egy még fel nem fedezett, tökéletesebb elméletnek. E két törvény kombinációja szolgáltatta, a mai elmélet dicsőségeként, az összes csodálatos egyezést a megfigyelésekkel, nem U egyedül. Ha U linearitása kiterjedne a makroszkopikus világra, akkor el kellene fogadnunk a krikettlabdák és hasonlók különböző helyzetei (vagy különböző spinjei stb.) komplex lineáris kombinációinak fizikai valóságát. A józan ész azt mondja nekünk, hogy a világ nem így viselkedik! A krikettlabdákat valóban nagyon jól közelítik a klasszikus fizika leírásai. Értelmesen, jól meghatározott helyzetük van, nem láthatók két helyen egyszerre, pedig a kvantummechanika lineáris törvényei ezt megengednék számukra. Ha az U és R eljárásokat átfogóbb törvénnyel kell helyettesíteni, akkor ennek az új törvénynek, ellentétben a Schrödinger-egyenlettel, nemlineáris jellegűnek kellene lennie (mert R hatása nemlineáris). Egyesek ellenvéleményen vannak, nagyon jogosan rámutatva arra, hogy a szabványos kvantumelmélet matematikai eleganciája a linearitás eredménye. Ám úgy érzem, meglepő volna, ha a kvantumelmélet a jövőben nem menne alapvető változáson keresztül – olyasvalami irányába, amelynek e linearitás csak közelítése. Vannak példák az ilyen változásra. Newton elegáns és hatékony egyetemes gravitációelmélete sokat köszönhetett annak a ténynek, hogy az elmélet erői lineáris módon adódnak össze. Einstein általános relativitáselmélete e linearitást mégis (bár kitűnő) közelítésre fokozta le – és Einstein elméletének eleganciája még a Newtonét is felülmúlja!
Nem csináltam titkot belőle, hogy azt hiszem, a kvantumelmélet rejtélyeinek megoldását egy javított elméletnek kell meghoznia. Noha ez talán nem a megszokott nézet, egyáltalán nem szokatlan. [Sokan a kvantumelmélet létrehozói közül is ezen a véleményen voltak. Einstein nézeteire már utaltam. Schrödinger (1935), de Broglie (1956) és Dirac (1939) szintén átmeneti jellegűnek tekintette az elméletet.] Ám ha úgy hiszi is valaki, hogy az elméletet módosítani kell, a megszorítások arra, hogy hogyan kell ezt csinálni, nagyon erősek. Talán valamiféle „rejtett változós” szemlélet végül elfogadható lesz. Ám az EPR-típusú kísérletek által mutatott nemlokalitás szigorú kihívást jelent a világ bármiféle „realisztikus” leírása számára, amely kényelmesen illeszkedhet egy közönséges téridőbe – összhangban a relativitáselmélet elveivel –, ezért azt hiszem, hogy sokkal radikálisabb változtatásra van szükség. Továbbmenve, kvantumelmélet és kísérlet között soha semmiféle ellentmondást nem találtak – persze ha nem tekintjük annak a lineárisan szuperponált krikettlabdák nyilvánvaló hiányát. Az én szemléletemben ez ténylegesen ellenbizonyíték! Ám önmagában nem sokat segít. Tudjuk, hogy a dolgok szubmikroszkopikus szintjén a kvantumos törvények uralkodnak; de a krikettlabdák szintjén a klasszikus fizika. Fenntartom, hogy valahol a kettő között új törvényt kell megértenünk, hogy meglássuk, hogyan olvad össze a kvantumos világ a klasszikussal. Hiszem azt is, hogy szükségünk van erre az új törvényre, ha valaha meg akarjuk érteni az értelmet! Mindehhez, úgy vélem, új nyomokat kell keresnünk.
A kvantumelmélet leírásában ebben a fejezetben teljesen a hagyományokat követtem, bár talán a szokásosnál nagyobb hangsúlyt kapott a geometriai és „realisztikus” nézőpont. A következő fejezetben a szükséges nyomok után próbálunk kutatni – amelyek hitem szerint útmutatást kell adjanak egy javított kvantummechanikáról. Otthonunk közeléből indulunk majd utunkra, de kénytelenek leszünk messzire utazni. Kiderül, hogy a tér nagyon távoli tartományait kell feltárnunk, és vissza kell utaznunk egészen az idők kezdetéig!
Penrose meg akar küzdeni a rejtelmekkel:
Fenntartom, hogy valahol a kettő között új törvényt kell megértenünk, hogy meglássuk, hogyan olvad össze a kvantumos világ a klasszikussal. - írja.
És most, ahogy ezt idézem villan belém, hogy a bejegyzésem címe:
Átmenet egyikből a másikba. -
majdnem ugyanezt mondja, írtam pedig a címet azelőtt, mielőtt a könyv újraolvasásába kezdtem volna. nem írom azt, hogy ez a "vak tyúk is talál szemet" esete, azt sem mondom, hogy ösztönös ráérzés, vagy a tudatalattimból felbukkanó valami. Ha Penrose megállapításainál, meglátásánál maradok, akkor ezt a címet tudatom R-függyvény szerinti működése adta, hiszen a könyvet januárban olvastam el először, azóta ott lapult a tartalma mélyen; mélyen, de ott volt az biztos...
7. Kozmológia és az idő aránya
Az idő folyása
Tudatosságérzésünk középpontjában áll az idő múlásának érzékelése. Úgy látszik, örökké előre mozgunk, egy határozott múltból egy bizonytalan jövőbe. A múltnak, úgy érezzük, vége, semmit sem lehet vele tenni. Változtathatatlan, és bizonyos értelemben már „ott kint” van. Jelenlegi tudásunk a múltról feljegyzéseinkből, emlékeinkből és az ezekből levont következtetéseinkből származhat, de a múlt valóságát nem szoktuk kétségbe vonni. A múlt egy dolog volt, és (most) már csak egy dolog lehet. Ami történt, megtörtént, most már sem mi, sem bárki más semmit nem tud tenni róla! A jövő viszont még határozatlannak látszik, lehet ilyen, lehet olyan. Ezt a „választást” talán egyértelműen rögzítik a fizikai törvények, talán részben hozzájárulnak saját döntéseink is (vagy a Jóisten); mindenesetre úgy látszik, a „választást” még meg kell tenni. Akármilyen irányban is dől el a jövő „valósága”, az mind csupán lehetőségnek látszik. Ahogy tudatosan észleljük az idő múlását, a hatalmas és látszólag meghatározatlan jövő legközelebbi része folyamatosan valósággá válik, belép a rögzített múltba. Olykor az lehet az érzésünk, hogy mi magunk személyesen „felelősek” vagyunk, mert némiképp befolyásoljuk annak a speciális jövőnek a kiválasztását, amely ténylegesen megvalósul, és állandósul a múlt valóságában. Még gyakrabban tehetetlen szemlélőnek érezzük magunkat – talán megkönnyebbültnek, megszabadulván a felelősségtől –, amikor a meghatározott múlt lassan, de kérlelhetetlenül nyomul előre a bizonytalan jövőbe.
Ám a fizika, ahogy ismerjük, más történetről szól. Minden sikeres egyenlete szimmetrikus az időben, egyformán jól használható mindkét irányban. A jövő és a múlt fizikailag teljesen egyenrangúnak látszik. Newton törvényei, Hamilton egyenletei, Maxwell egyenletei, Einstein általános relativitáselmélete, Dirac egyenlete, Schrödinger egyenlete – mind változatlanok maradnak, ha az idő irányát megfordítjuk (az időt jelentő t koordinátát –t-vel helyettesítjük). Az egész klasszikus mechanika a kvantummechanika „U” részével együtt az időben teljesen megfordítható. Az kérdéses, hogy a kvantummechanika „R” része megfordítható-e. Ez központi kérdés lesz a következő fejezetbeli vizsgálatokban. Egyelőre kerüljük ki a problémát azzal, amit a tárgykör „hagyományos bölcsességének” lehet tekinteni – nevezetesen, hogy az első benyomások ellenére az R műveletet is időszimmetrikusnak kell venni (vö. Aharonov, Bergmann és Lebowitz 1964). Ha ezt elfogadjuk, akkor úgy látszik, máshol kell keresnünk, ha meg akarjuk tudni, fizikai törvényeink szerint hol kell legyen a múlt és jövő közötti megkülönböztetés.
Mielőtt ezzel foglalkoznánk, nézzünk meg egy másik rejtélyes ellentmondást időérzékelésünk és a modern fizikai elmélet állításai között. A relativitáselmélet szerint olyan, hogy „most,” valójában egyáltalán nincs is. E fogalomhoz legközelebb álló dolog egy megfigyelő „egyidejű tere” a téridőben, ahogy az az 5.21. ábrán látható, de az függ a megfigyelő mozgásától! A „most” nem ugyanaz az egyik és másik megfigyelő szerint!135 Két téridőeseményt, A-t és B-t az U megfigyelő megítélhet úgy, hogy B a meghatározott múlthoz, A a bizonytalan jövőhöz tartozik, míg egy másik, V megfigyelő úgy, hogy A tartozik a rögzített múlthoz, B a bizonytalan jövőhöz! Nem állíthatjuk egyértelműen, hogy az A és B események egyike bizonytalan, a másik meghatározott (lásd 7.1. ábra).
Emlékezzünk vissza az 5. fejezetben tárgyaltakra és az 5.22. ábrára. Két ember megy el az utcán egymás mellett; az egyik szerint egy Androméda űrhajó már elindult útjára, a másik szerint még a döntés sem született meg az űrhajó indításáról. Hogyan lehet bizonytalan a döntés eredménye? Ha az egyik szerint a határozatot már meghozták, akkor bizonytalanságról nem lehet szó. Az űrhajó indulása elkerülhetetlen tény. Valójában még egyik ember sem tudhat az űrhajó indulásáról. Csak később tudhatják meg, amikor távcsöveik elárulják, hogy az űrhajó már valóban úton van. Ekkor visszagondolhatnak véletlen találkozásukra, és levonhatják a következtetést, hogy akkor egyikük szerint a döntés a bizonytalan jövőben volt, míg másikuk szerint a biztos múltban. Volt-e akkor bizonytalanság a jövőt illetően? Vagy mindkét ember jövője már „rögzített” volt?
Kezd látszani, hogy ha egyáltalán valami meghatározott, akkor a teljes téridő valóban az kell legyen! Nem lehet „bizonytalan” jövő. Az egész téridő rögzített kell legyen mindenféle bizonytalanság nélkül. Úgy látszik, valójában ez volt Einstein saját következtetése (vö. Pais 1982). Mi több, az időnek egyáltalán nincs folyása. Csak „téridő” van – semmi lehetősége olyan jövőnek, amelynek tartományába elkerülhetetlenül hatol be egy meghatározott múlt! (Az Olvasó megkérdezheti, mi a szerepük ebben az egészben a kvantummechanika „bizonytalanságainak”. A kvantummechanika által felvetett kérdésekre a következő fejezetben majd visszatérek. Egyelőre jobb, ha tisztán klasszikus képben gondolkodunk.)
Én úgy látom, komoly eltérések vannak aközött, amit tudatosan érzünk az idő folyásáról, és amit (csodálatosan pontos) elméleteink állítanak a fizikai világ valóságáról. Ezek az eltérések biztosan mondanak valami mélyet a fizikáról, és ezzel feltehetően alá kell támasztanunk tudatos érzékelésünket – feltéve (mint hiszem), hogy ami az alapjául szolgál ezeknek az érzékeléseknek, az valóban megérthető a fizika megfelelő ágának segítségével. Az legalábbis világosan látszik, hogy akármilyen fizika is működjék, annak lényeges időaszimmetrikus eleme kell legyen, azaz megkülönböztetést kell tegyen múlt és jövő között.
Ha a fizika egyenleteiből ez nem látszik – sőt ha maga a „jelen” fogalma olyan kényelmetlenül illik a relativitáselméletbe –, akkor hol a csudában keressünk olyan fizikai törvényeket, amelyek jobban összhangban vannak azzal, amit a világból felfogni látszunk? Valójában a dolgok nem annyira ellentmondásosak, amennyire, úgy tetszhet, én hangoztatom. Fizikai megértésünk fontos egyéb elemeket is tartalmaz, nem csupán az időfejlődés egyenleteit – és ezek között valóban vannak időaszimmetriát tartalmazóak. A legfontosabb az, amelyet a termodinamika második főtétele néven ismerünk. Próbáljuk megérteni, mit mond ez a törvény.
A múltnak, úgy érezzük, vége, semmit sem lehet vele tenni. Változtathatatlan, és bizonyos értelemben már „ott kint” van. Jelenlegi tudásunk a múltról feljegyzéseinkből, emlékeinkből és az ezekből levont következtetéseinkből származhat, de a múlt valóságát nem szoktuk kétségbe vonni. -írja.
"Mélységes mély a múltnak kútja" - így kezdi a József és testvérei-t Thomas Mann. És a gyermekkor, meg a szerelem emlékei. A '...mi lett volna ha...'
„Régi nyarakon” – mondja egy Illés-szám, vagy Cseh Tamás?
...Egy kattintás az Interneten és már olvashatod is: A „régi nyarakon” Cseh Tamás/Bereményi Géza
A hatvanas évek című [1977-ben írt] számában hangzik el. Tök jó ez az Internet gondolja elsőre az ember, hiszen „minden” tudáshoz hozzájuthatsz, csak egy kattintás. Csak egy kattintás. Pedig nem is olyan jó, cáfolod magad rögtön, mert kényelmessé tesz, nem erőlködsz, nem kutatsz az agyadban elraktározott tudás, vagy emlékek után, hanem kattintasz. Még szerencse, hogy ez csak a rajtad kívül létező világban rögzített tudásra és emlékekre érvényes. Te nem úgy működsz. Nem kattintásra. Mert itt van például ez a „Régi nyarakon” …ami akár a boglári mólót is idézhetné: 69 nyara, naplemente, aranyhíd a vízen, közben szól az Omega szám: a Gyöngyhajú lány. És hozzád egy másik lány is szól, aki nincs ott veletek, akinek alig volt része ilyesmiben a hatvanas, hetvenes években.
„Régi nyarakon” – mondja egy Illés-szám, vagy Cseh Tamás? - mennyivel összetettebb ez, hogy így jött elő belőled, mint az amit végül az Internetről megtudtál. És ahogy ezt írom a "szól" szó megint előhoz egy dalt:
"...szól a rádió...", itt is van tippem, hogy ki énekli, de nem olyan éles, mint az előbbi...megint egy kattintás:
||: Szól a rádió, szól a rádió. :|| - ez meg egy LGT szám. És nincs is benne a háború...pedig az előbb itt belül még együtt szólt azzal a számmal...valahogy így: '...régi kép, két háború...' Hívószavak, kíváncsi vagyok, hogy erre mit hoz elő a kereső:
„Egy régi kép: egy kisgyerek,
Ki tudja már, miért nevet.
Egy másik arc: egy kisleány,
Ki tudja már, miért vidám.”
…
„S lesz két gyerek: egy kisfiú,
Egy kisleány, s két háború.”
hát persze:
1969 Régi dal, Szörényi Szabolcs/Bródy János énekli Koncz Zsuzsa. És az emlékeket burkoló szövet most már egyre több mindent enged onnan előugrani: ...
„Nézd: milyen az ég
estefelé
ibolyakék
milyen az ég”…a Színes ceruzák-ból. Szól a rádió…valamikor ugyanabban az évben, vagy még 68 nyara volt? A Körös melletti kukoricaföld szélén a valamelyik akácfára fölakasztott Sokol rádió szól és nem Little Richard, hanem Koncz Zsuzsa énekel. Meleg van, kapáljuk a kukoricát öt unokák és nem is érezzük a fáradtságot a forróságot, hanem a végtelen könnyűséget, ami körülvesz bennünket. Nyár van, vakáció.
És akkor a jövőről:
A jövő viszont még határozatlannak látszik, lehet ilyen, lehet olyan. Ezt a „választást” talán egyértelműen rögzítik a fizikai törvények, talán részben hozzájárulnak saját döntéseink is (vagy a Jóisten); mindenesetre úgy látszik, a „választást” még meg kell tenni. Akármilyen irányban is dől el a jövő „valósága”, az mind csupán lehetőségnek látszik. Ahogy tudatosan észleljük az idő múlását, a hatalmas és látszólag meghatározatlan jövő legközelebbi része folyamatosan valósággá válik, belép a rögzített múltba. Olykor az lehet az érzésünk, hogy mi magunk személyesen „felelősek” vagyunk, mert némiképp befolyásoljuk annak a speciális jövőnek a kiválasztását, amely ténylegesen megvalósul, és állandósul a múlt valóságában. Még gyakrabban tehetetlen szemlélőnek érezzük magunkat – talán megkönnyebbültnek, megszabadulván a felelősségtől –, amikor a meghatározott múlt lassan, de kérlelhetetlenül nyomul előre a bizonytalan jövőbe. -írja.
...
Ahogy tudatosan észleljük az idő múlását, a hatalmas és látszólag meghatározatlan jövő legközelebbi része folyamatosan valósággá válik, belép a rögzített múltba.
Megint itt van:
Átmenet egyikből a másikba.
Thomas Wolfe: Az időről és a folyóról című könyvét is nagyon szerettem, talán 72-ben vagy 73-ban olvastam.
„Az idő, az idő múlása, visszahozhatatlansága, az emberélet villanásnyi rövidsége, a természet időtlen végtelensége – ezek a problémák foglalkoztatják az írót itt is, úgy, mint minden művében.
Tulajdonképpen mindig önmagát írja. A Nézz vissza, angyalban gyermekkorát, itt egyetemi éveit, európai útját és hazatértében találkozásait a szerelemmel. Csodálatos sodrású lírai prózáját az ő kedvelt képeivel: a kontinenseket átszelő száguldó vonattal, félelmetes sebességgel örvénylő áradó folyóval szokták jellemezni. Mind a kettő találó. Aki olvassa, soha nem felejti el.”
Igen, az éjszakai vonat utazás képei, emlékszem a könyvből. Ott voltam én is azokon a vonatokon (mindig is szerettem az éjszakai vonat utakat). József Attila ezt kívülről nézi, jobban mondva olyan ’kint is vagyok, bent is vagyok’ módra:
Vasútnál lakom. Erre sok |
vonat jön-megy és el-elnézem, |
hogy' szállnak fényes ablakok |
a lengedező szösz-sötétben. |
Igy iramlanak örök éjben |
kivilágított nappalok |
s én állok minden fülke-fényben, |
én könyöklök és hallgatok. |
|
de mielőtt a minden hiábavaló, a "minden egész eltörött" [Ady] érzése eluralkodhatna rajtunk rögtön meg is vigasztal,hogy ez a pesszimista következtetés nem teljesen helyénvaló!
Mi az entrópia?
Mi hát pontosan egy fizikai rendszer entrópiája? Láttuk, hogy a látható rendezetlenség egyfajta mértéke, de mert ilyen pontatlan kifejezéseket használok, mint „látható” és „rendezetlenség”, ezért úgy nézhet ki, hogy az entrópia nem lehet igazán nagyon világos, tudományos mennyiség. Van a második főtételnek is egy olyan tartalma, amely az entrópiafogalom pontatlanságát látszik jelezni: az ún. irreverzibilis rendszerek azok, amelyek entrópiája nem állandó, hanem nő. Mit jelent az, hogy „irreverzibilis”? Ha figyelembe vesszük az összes részecske részletes mozgásait, akkor minden rendszer reverzibilis! A gyakorlatban azt mondjuk, hogy az üveg leesése és széttörése, vagy a tojás megsülése, vagy a cukor feloldódása a kávéban mind irreverzibilis; míg kisszámú részecske egymással való rugalmas ütközését reverzibilisnek tekintjük, mint ahogy sok más jól ellenőrzött folyamatot is, amelyekben az energia nem alakul át hővé. Az „irreverzibilis” szó alapjában arra a tényre utal, hogy a rendszerben az egyes részecskék mozgásainak minden lényeges részletét nem lehet nyomon követni, sem szabályozni. Ezekre a rendezetlen mozgásokra utal a „hő” kifejezés. Az irreverzibilitás így pusztán „gyakorlati” dolognak látszik. A gyakorlatban nem tudunk „visszanyersíteni” egy tojást, bár ez a mechanika törvényei szerint tökéletesen megengedett folyamat. Függ-e entrópiafogalmunk attól, hogy mi gyakorlati, és mi nem az?
Idézzük fel az 5. fejezetből, hogy az energia fogalmára, csakúgy mint az impulzuséra és impulzusmomentuméra, pontos matematikai meghatározás adható a részecske helyzete, sebessége, tömege és az erők segítségével. Ám hogyan tegyük ugyanezt a „látható rendezetlenség” fogalmánál, ami pedig szükséges lenne ahhoz, hogy az entrópiát matematikailag pontossá tegyük? Biztos, hogy ami „nyilvánvaló” az egyik megfigyelőnek, az nem feltétlenül az egy másiknak. Nem függ-e ez a pontosságtól, amellyel az egyes megfigyelők a vizsgált rendszert mérni képesek? Egy megfigyelő jobb mérőműszerekkel sokkal részletesebb információt szerezhet egy rendszer mikroszkopikus alkotórészeiről, mint egy másik. Egy rendszer „rejtett rendjéből” több lehet nyilvánvaló az egyik megfigyelő számára, mint a másikéra – és eszerint ő alacsonyabb entrópiát állapít meg, mint a másik. Úgy látszik, hogy a különböző megfigyelők esztétikai ítéletei is belejátszanak abba, mit tartanak „rendnek” inkább, mint „rendetlenségnek”. Elképzelhetünk művészeket, akik szerint az összetört pohár töredékei sokkal szebben elrendezettek, mint volt a förtelmesen csúnya pohár az asztal szélén állva! Valóban csökkent az entrópia az ilyen művészi érzékű megfigyelő ítélete szerint?
E szubjektivitási problémákat nézve figyelemre méltó, hogy az entrópia fogalmának egyáltalán van haszna a pontos tudományos leírásokban – és biztos, hogy van! A használhatóság oka az, hogy egy rendszerben a rendből a rendezetlenség felé irányuló változások a részecskék részletes helyzeteiben és sebességeiben kifejezve végletesen óriásiak, és (majdnem minden körülmény között) tökéletesen elmosnak minden ésszerű nézőpontkülönbséget abban, hogy a makroszkopikus skálán mi, vagy mi nem „látható rend”. Speciálisan, amiről a művész vagy a tudós ítélkezik, hogy az ép vagy az összetört üveg-e a szabályosabb elrendezés, majdnem semennyire sem érinti az entrópia mértékét. A messze legfontosabb járulékot a részecskék véletlenszerű mozgása adja, amely a kis hőmérséklet-emelkedést eredményezi, és a víz szétszóródása, amikor a pohár és a víz a földre kerül.
Hogy az entrópiáról pontosabban beszélhessünk, térjünk vissza a fázistér fogalmához, amelyet az 5. fejezetben említettünk először. Emlékezzünk arra, hogy egy rendszer fázistere rendesen óriási dimenziószámú tér, amelynek minden pontja egy teljes fizikai állapotot ábrázol annak minden apró részletével. Egyetlen fázispont megadja a szóban forgó fizikai rendszert alkotó minden egyedi részecske minden hely- és impulzuskoordinátáját. Az entrópia fogalmához szükségünk van a látható (azaz makroszkopikus) tulajdonságok szempontjából azonosnak látszó minden állapot összegyűjtésére. Fázisterünket úgy kell tehát felosztanunk tartományokra (vö. 7.3. ábra), hogy tetszőleges tartományhoz tartozó, különböző pontok olyan fizikai rendszereket ábrázoljanak, amelyek bár különböznek a részecskekonfigurációk és mozgások apró részleteiben, a makroszkopikusan megfigyelhető tulajdonságokat tekintve azonosak. A szemmel látható szempontjából egyetlen tartomány minden pontját úgy tekintjük, mint amelyek ugyanazt a fizikai rendszert ábrázolják. A fázistér ilyen tartományokra való felosztását durva szemcsézésnek nevezik.
-szer, ha a doboz egy 1 köbméteres kocka, közönséges légköri nyomású és hőmérsékletű levegőt tartalmaz egyensúlyban, és a sarok körüli tartomány egy 1 köbcentiméteres kocka!
Hogy méltányoljuk a fázistér-térfogatok ilyen különbségét, képzeljünk el egy egyszerűsített helyzetet, amikor golyókat osztunk szét cellákba. Tegyük fel, hogy minden cella vagy üres, vagy egyetlen golyót tartalmaz. A golyók a gázmolekulákat, a cellák a golyók által a dobozban elfoglalható különböző helyzeteket képviselik. Válasszuk ki a cellák egy kis speciális csoportját; ezek a doboz sarkában elfoglalható helyzeteket ábrázolják. A határozottság kedvéért tegyük fel, hogy a celláknak pontosan a tizedrésze speciális – legyen mondjuk n speciális cella és 9n nem speciális (lásd 7.4. ábra). Mondjuk m golyót akarunk a cellák között véletlenszerűen szétosztani, és keressük annak valószínűségét, hogy mindegyik golyó speciális cellába kerül. Ha csak egy golyó van és tíz cella (így egyetlen speciális cellánk van), akkor e valószínűség nyilván egytized. Ugyanez igaz, ha egy golyó van és 10n számú cella (így n speciális). Ezért a csak egy atomot tartalmazó „gáz” esetében a speciális tartomány, amely annak felel meg, hogy a gáz „a sarokba van bezsúfolva”, a „fázistér” teljes térfogatának egytized részét tenné ki. De ha növeljük a golyók számát, akkor annak valószínűsége, hogy mindegyik speciális cellába kerül, nagyon lecsökken. Két golyóra, mondjuk húsz cellával136 (amiből kettő speciális) (m = 2, n = 2) a valószínűség 1/190, száz cellával (tíz speciálissal) (m = 2, n = 10) 1/110; nagyon nagy számú cellával 1/100. Így egy két atomból álló „gáz” esetén a speciális tartomány térfogata a „fázistér” teljes térfogatának egyszázad része. Három golyó és harminc cella (m = 3, n = 3) esetén 1/4060; nagyon nagy számú cella esetén 1/1000 lesz – így egy három atomból álló „gáznál” a speciális tartomány térfogat a „fázistér” térfogatának egy ezrede. Négy golyóval, nagyon nagy számú cellával a valószínűség 1/10 000. Öt golyóval és nagyon nagy számú cellával 1/100 000, és így tovább. m golyóra és nagyon nagy számú cellára a valószínűség 1/10m, így egy m atomból álló „gáznál” a speciális tartomány térfogata 1/10m-szerese a „fázistér” térfogatának. (Ez akkor is érvényes, ha az „impulzust” is figyelembe vesszük.)
Alkalmazhatjuk ezt az előbb vázolt helyzetre, egy dobozba zárt igazi gázra, csak most a speciális tartomány egytized helyett csak egymilliomod (azaz 1/1 000 000) része a teljesnek (azaz egy köbcentiméter egy köbméterben). Ezért a valószínűség 1/10m helyett most 1/(1 000 000)m, azaz 1/106m. Közönséges levegőnél dobozunkban kb. 1025 molekula lenne összesen, így m = 1025. Tehát a fázistér azon speciális tartományának térfogata, amely azt a helyzetet képviseli, amikor az egész gáz a sarokban gyűlik össze, csak
1/1060 000 000 000 000 000 000 000 000
része a teljes fázistérnek!
Egy állapot entrópiája azon tartomány V térfogatának mértéke, amely tartalmazza az állapotot ábrázoló fázistérpontot. Tekintve az e térfogatok közötti hatalmas eltéréseket, talán semmi hátrányt nem jelent, hogy az entrópiát nem a térfogattal, hanem a térfogat logaritmusával vesszük arányosnak:
entrópia = k logV.
Így a számok ésszerűbben néznek ki. 10 000 000 logaritmusa137 például csak 16 körül van. k az ún. Boltzmann-állandó. Értéke kb. 10–23 J/K (vagyis joule per Kelvin-fok). Hogy logaritmust vettünk, annak lényeges oka az, hogy így az entrópia független rendszerekre additív mennyiség. Két teljesen független fizikai rendszerre az egyesített rendszer teljes entrópiája az egyes rendszerek entrópiáinak összege. (Ez a logaritmusfüggvény alapvető algebrai tulajdonságának következménye: logAB = logA + logB. Ha a két rendszer saját fázisterében A, illetve B térfogatú tartományhoz tartozik, akkor az együttes rendszernek megfelelő fázistér-térfogat az AB szorzat lesz, mert az egyik rendszer minden lehetőségét külön-külön párosítani kell a másik rendszer minden lehetőségével; így az együttes rendszer entrópiája valóban a két entrópia összege.)
A fázistérbeli tartományok méretei közötti óriási eltérések az entrópiában már ésszerűbb formában jelentkeznek. Köbméteres dobozba zárt gázunk entrópiája csak mintegy 1400 JK–1-nel (= 14k ∙ 1025) nagyobb, mint a köbcentiméter méretű „speciális” tartományba sűrített gáz entrópiája [mert
Hogy e tartományok tényleges entrópiaértékeit megadjuk, el kellene gondolkodnunk egy kicsit azon, milyen egységeket válasszunk (méterek, joule-ok, kilogrammok, kelvinek stb.). Ez most nem idetartozó kérdés, és az elképesztően nagy entrópiaértékek mellett, amelyeket rövidesen megadok, lényegében egyáltalán nem jelent különbséget, hogy milyen egységeket választunk. Azonban a határozottság (és a szakértők) kedvéért hadd mondjam, hogy a kvantummechanika szabályainak megfelelő természetes egységeket választok, amelyekben a Boltzmann-állandó egységnyi:
k = 1.
137 Az itt használt logaritmus a természetes logaritmus, azaz amelynek alapja nem 10, hanem e = 2,7182818285…, e különbség azonban teljesen lényegtelen. Egy n szám x = logen természetes logaritmusa az a kitevő, amelyre e-t kell emelni, hogy n-et kapjunk, más szóval az ex = n egyenlet megoldása.
A második főtétel működésben
Tegyük most fel, hogy egy rendszert nagyon speciális helyzetből indítunk, például az egész gázt a doboz egyik sarkából. A következő pillanatban a gáz szétterjed, és gyorsan egyre nagyobb és nagyobb térfogatot foglal el. Rövid idő után beáll a hőmérsékleti egyensúly. Hogy néz ki ez a fázistérben? A gáz minden részecskéjének teljes, részletes hely- és mozgásállapotát minden szakaszban egyetlen pont írja le a fázistérben. Ahogy a gáz fejlődik, ez a pont vándorol a fázistérben, pontos vándorlása leírja a gáz minden részecskéjének teljes történetét. A pont egy nagyon kicsi tartományból indul – amely az olyan lehetséges kezdeti állapotok összességét képviseli, amelyekben az egész gáz a doboz egyik sarkában van. Ahogy kezd szétterjedni, mozgó pontunk egy lényegesen nagyobb fázistér-térfogatba lép be, ez azoknak az állapotoknak felel meg, amelyekben a gáz már egy kicsit szétterjedt a dobozban. A fázistérpont mind nagyobb és nagyobb térfogatokba lép be, ahogy a gáz tovább terjed szét, mindegyik új térfogat mellett eltörpül mindegyik megelőző – az arányok elképesztően nagyok (lásd 7.5. ábra)! Minden esetben, amikor a pont nagyobb térfogatba lépett át, lényegében nincs esély arra, hogy megtalálja bármelyik előző kisebbet. Végül elvész a fázistér legnagyobb térfogatában – ez felel meg a hőmérsékleti egyensúlynak. Ez a térfogat gyakorlatilag elfoglalja az egész fázisteret. Lényegében biztosra vehető, hogy véletlenszerű vándorlása során fázispontunk ésszerű időn belül nem talál meg egyetlen kisebb térfogatot sem. Ha egyszer elérte a hőmérsékleti egyensúlyt, akkor ez az állapot örökre megmarad. Látjuk, hogy a rendszer entrópiája, a fázistér megfelelő tartománya térfogatának logaritmikus mértéke megtartja a növekedés e kérlelhetetlen tendenciáját, ahogy az idő halad előre.138
Úgy látszik, most magyarázatot találtunk a második főtételre! Feltételezhetjük ugyanis, hogy fázistérpontunk nem valami speciális módon mozog, és ha egy piciny fázistér-térfogatból indul, amelyhez kis entrópia tartozik, akkor elsöprő valószínűséggel egyre nagyobb és nagyobb fázistér-térfogatokba jut, ami fokozatosan növekvő entrópiaértékeknek felel meg.
Van azonban egy kicsit furcsa abban, amit most ezzel az érveléssel látszólag levezettünk. A következmény ugyanis időaszimmetrikus. Az entrópia a pozitív időirányban nő, ezért a fordított időirányban csökkennie kell. Honnan jön ez az időaszimmetria? Ilyen fizikai törvényt biztosan nem vezettünk be. Csupán abból ered, hogy a rendszer egy nagyon speciális (ugyanis alacsony entrópiájú) állapotból indult; így figyeltük fejlődését a jövő irányában, és azt találtuk, hogy az entrópia nő. Ez összhangban van a rendszerek viselkedésével világegyetemünkben. De ugyanezt az érvelést a fordított időirányra is alkalmazhattuk volna. Előírhatnánk, hogy a rendszer egy adott időpontban egy alacsony entrópiájú állapotban van, de most azt kérdezzük, mi az állapotok legvalószínűbb sorozata, amely ezt megelőzte.
Próbáljunk ezen a fordított módon érvelni. Az alacsony entrópiájú állapot legyen az, mint előbb, hogy az egész gáz a doboz egyik sarkában van. Fázistérpontunk is ugyanabban a nagyon pici tartományban van, ahonnan az előbb indítottuk. Próbáljuk azonban most előző történetét nyomon követni. Ha elképzeljük, hogy a fázistérpont ugyanolyan véletlenszerűen ugrabugrál, mint előbb, akkor a mozgást az időben visszafelé nyomon követve azt várjuk, hogy hamarosan eléri ugyanazt a lényegesen nagyobb fázistér-térfogatot, mint az előbb, megfelelően annak, hogy a gáz egy kissé szétterjed a dobozban, de nem kerül hőmérsékleti egyensúlyba, azután a nagyobb és nagyobb térfogatokat; mindegyik új térfogat teljesen eltörpíti a megelőzőt, és visszafelé távol az időben a legnagyobb tartományban találjuk, amelyik a hőmérsékleti egyensúlyt képviseli. Most látszólag azt vezettük le, hogy ha egy időpontban az egész gáz a doboz sarkába volt zsúfolva, akkor a legvalószínűbb módja annak, ahogy idekerült, az az, hogy hőmérsékleti egyensúlyból indult, azután kezdett egyre jobban és jobban összesűrűsödni a doboz egyik végében, végül összegyűlt a sarokban. Az entrópiának az egész idő alatt csökkennie kellett; a magas egyensúlyi értékről indult, utána fokozatosan csökkent, míg elérte a nagyon alacsony értéket, amely annak felel meg, hogy a gáz összesűrűsödik a doboz kis sarkában!
Világegyetemünkben természetesen semmi ilyen nem történik! Az entrópia nem csökken, hanem növekszik. Ha egy időpontban az egész gáz össze volna zsúfolva a doboz egyik sarkában, akkor az ezt megelőző helyzet sokkal valószínűbben az lehetett volna, hogy egy fal tartotta ott tartósan, és a falat hirtelen eltávolították. Vagy esetleg megfagyott vagy folyékony állapotban volt ott, és gyors melegítés hatására változott gázneművé. Ezen alternatív lehetőségeknél az entrópia a megelőző állapotokban még alacsonyabb. A második főtétel érvényesül, az entrópia az egész idő alatt növekszik – azaz a fordított időirányban csökken. Most látjuk, hogy gondolatmenetünk teljesen rossz választ eredményezett! Azt mondta nekünk, hogy a legvalószínűbben úgy jutunk a doboz sarkában összesűrűsödő gázhoz, ha hőmérsékleti egyensúlyból indulunk, ezután az entrópia állandó csökkenése mellett a gáz összegyűlik a sarokban. Ám való világunkban rendkívül valószínűtlen, hogy ez megtörténik. A valóságban a gáz egy még kevésbé valószínű (azaz alacsonyabb entrópiájú) állapotból indulna, az entrópia állandóan növekedne, míg elérné azt az értéket, amelyet a sarokban összegyűlt gáz képvisel.
Gondolatmenetünk jónak bizonyult, amikor azt a jövő irányába alkalmaztuk, de a múlt irányába már nem megy a dolog. A jövő irányában helyesen jósoltuk, hogy amikor a gáz a sarokból indul, akkor a legvalószínűbben az történik, hogy beáll a hőmérsékleti egyensúly, és nem az, hogy hirtelen megjelenik egy válaszfal, vagy hogy a gáz hirtelen megfagy vagy folyékonnyá válik. Ezek a bizarr lehetőségek éppen azt az entrópiacsökkentő viselkedést képviselnék, amelyet fázistér-meggondolásunk, helyesen, kizárni látszik. Ám a múlt irányában éppen ezek a „bizarr” alternatívák azok, amelyek valószínűen megtörténnek – és számunkra egyáltalán nem látszanak bizarrnak. Fázistér-gondolatmenetünk teljesen rossz választ adott, amikor megpróbáltuk a fordított időirányban alkalmazni!
Ez világos módon megkérdőjelezi az eredeti érvelést. A második főtételt nem vezettük le. A gondolatmenet ténylegesen azt mutatta meg, hogy egy adott alacsony entrópiájú állapotból, mondjuk egy doboz sarkában összezsúfolt gázból indulva, a rendszert megszorító bármilyen más tényező hiányában az entrópia növekedését várjuk mindkét időirányban (lásd 7.6. ábra). Az érvelés a múlt irányában nem működött, pontosan azért, mert ott voltak ilyen tényezők. Valóban volt valami kényszerítő a rendszer számára a múltban. Valami kényszerítette arra, hogy entrópiája a múltban alacsony legyen. A magas entrópia felé törekvés a jövő irányában nem meglepő. A magas entrópiájú állapotok bizonyos értelemben a „természetes” állapotok, amelyek nem igényelnek további magyarázatot. Ám a múlt alacsony entrópiájú állapotai rejtélyesek. Mi kényszerítette világunkat, hogy entrópiája a múltban olyan alacsony legyen? Az olyan állapotok mindennapos jelenléte, amelyekben az entrópia abszurd módon alacsony, az általunk lakott világegyetem meglepő sajátsága – noha ezek az állapotok annyira közhelynek számítanak, annyira megszokottak számunkra, hogy nem hajlunk azokat meglepőeknek tekinteni. Mi magunk képtelenül kicsiny entrópiájú képződmények vagyunk! A fenti gondolatmenet azt mutatja, hogy nem kellene meglepődnünk, ha egy adott alacsony entrópiájú állapotból indulva az entrópia egy későbbi időpontban magasabb lesz. Azon kellene meglepődnünk, hogy az entrópia mind képtelenebbül kisebb, minél régebben vizsgáljuk azt a múltban!
Mi az az entrópia?- kérdezem Lalit. Mondja, hogy mi, de azt is, hogy nagyon nehezen felfogható valami egyelőre, főleg ahogyan a professzor magyarázza, és a könyve is legalább olyan nehézkes, mint ő maga. Penrose szemléletesen írja le, és amit itt az entrópiáról, és a termodinamika második főtételéről mond, azt a későbbiekben bemutatott sejtései egyik alapvető bevezetésének, alátámasztásának szánja.
Az alacsony entrópia eredete a világegyetemben
Próbáljuk megérteni, miből ered világunknak ez a „meglepően” alacsony entrópiája. Kezdjük magunkkal! Ha magyarázatot találunk a saját alacsony entrópiánkra, akkor azt is látni fogjuk, mi az oka a válaszfallal elzárt gáz alacsony entrópiájának – vagy a vizespohárénak az asztalon, a serpenyő fölött tartott tojásénak, a kávéscsésze fölött tartott kockacukorénak. Mindegyik esetben közvetlenül vagy közvetve egy személy vagy személyek (vagy esetleg egy tyúk!) felelősek a dologért. Nagymértékben a bennünk lévő alacsony entrópia egy részét használtuk arra, hogy létrehozzuk ezeket az alacsony entrópiájú állapotokat. Közrejátszhattak egyéb tényezők is. Esetleg vákuumszivattyúval szívtuk át a gázt a doboz sarkába a válaszfal beillesztése után. Ha a szivattyút nem kézzel működtettük, akkor valamilyen „fosszilis fűtőanyagot” (például olajat) égettünk el, hogy biztosítsuk a szükséges alacsony entrópiájú energiát. Esetleg elektromos pumpát alkalmaztunk, amely közvetve egy atomerőmű uránium tüzelőanyagában tárolt alacsony entrópiájú energiát használta fel. Később majd visszatérek ezekre az egyéb alacsony entrópiájú forrásokra, először azonban a saját magunk alacsony entrópiáját vegyük szemügyre.
Mi hát az eredete a saját alacsony entrópiánknak? Testünk szervezettsége az élelemből származik, amit megeszünk, és a levegőből, amit belélegzünk. Gyakran halljuk, hogy élelem és oxigénfelvételünkből energiát nyerünk, de ez nem minden értelemben teljesen helyénvaló. Igaz, hogy az elfogyasztott élelem és a felvett oxigén összekombinálódva energiával lát el bennünket. Ám ennek az energiának a legnagyobb része ismét elhagyja testünket, főleg hő formájában. Minthogy az energia megmarad, és minthogy testünk tényleges energiatartalma felnőtt életünk során többé-kevésbé állandó, egyszerűen nincs rá szükségünk, hogy hozzáadjunk ahhoz. Nincs szükségünk több energiára, mint amennyivel már rendelkezünk. Amikor hízunk, akkor valójában növeljük energiatartalmunkat – de ezt rendszerint nem tekintjük kívánatosnak! Szintén jelentősen növeljük, amikor gyermekségünkből felnőtté válva felépítjük testünket; de most nem erről van szó. A kérdés az, hogyan tartjuk magunkat életben rendes (főként felnőtt) életünk során. Ehhez nincs szükségünk arra, hogy energiatartalmunkhoz még bármennyit is hozzátegyünk.
Arra azonban szükségünk van, hogy pótoljuk az energiát, amelyet hő formájában folyamatosan elvesztünk. Valójában minél „energikusabbak” vagyunk, annál több energiát veszítünk ebben a formában. Mindezt pótolnunk kell. A hő az energia leginkább rendezetlen, azaz a legnagyobb entrópiájú formája. Az energiát alacsony entrópiájú formában (élelemben, oxigénben) vesszük fel, és magas entrópiájú formában (hőben, szén-dioxidban, váladékokban) adjuk le. Nincs szükségünk rá, hogy környezetünktől energiát nyerjünk, mert az energia megmarad. Ám folyamatosan küzdünk a termodinamika második főtétele ellen. Az entrópia nem marad meg, állandóan növekszik. Hogy magunkat életben tartsuk, entrópiánkat alacsonyan kell tartanunk. Ezt úgy érjük el, hogy az élelem és a légköri oxigén alacsony entrópiás kombinációját vesszük magunkhoz, ezzel tápláljuk magunkat, és az energiát nem halmozzuk fel, hanem magas entrópiájú formában leadjuk. Ily módon testünk entrópiáját nem engedjük emelkedni, és képesek vagyunk megőrizni (sőt növelni) belső szervezettségünket (lásd Schrödinger 1967).
Honnan származik az alacsony entrópia utánpótlása? Ha az elfogyasztott élelem történetesen hús (vagy gomba!), akkor ez valamely további külső, alacsony entrópiájú forrásból táplálkozik, így őrzi meg alacsony entrópiás szerkezetét. A külső alacsony entrópia eredetének problémáját így csak eltoltuk valahová máshova. Ezért tételezzük fel, hogy mi (vagy az állat vagy a gomba) növényt fogyasztunk. Mindnyájan – közvetlenül vagy közvetve – a legteljesebb hálával tartozunk a zöld növényeknek okosságukért: a légköri szén-dioxidot veszik fel, elválasztják az oxigént a széntől, és a szenet használják fel anyaguk felépítésére. Ez az eljárás, a fotoszintézis az entrópia nagy csökkenését idézi elő. Mi magunk is hasznot húzunk ebből a szétválasztásból egyszerűen azzal, hogy az oxigént és a szenet testünkön belül újra egyesítjük. Hogyan képesek a zöld növények véghezvinni ezt az entrópiacsökkentő varázslatot? A napfény segítségével. Ez viszonylag alacsony entrópiájú formában szállítja a Földre az energiát, nevezetesen a látható fény fotonjaiban. A Föld és lakói nem őrzik meg ezt az energiát, hanem (egy idő után) visszasugározzák az egészet az űrbe. A visszasugárzott energia azonban magas entrópiájú, az ún. „sugárzási hő” – ami infravörös fotonokat jelent. A közhiedelemmel ellentétben a Föld (lakóival együtt) nem nyer energiát a Napból! A Föld alacsony entrópiájú formában felvesz energiát, majd az egészet visszaköpi az űrbe, de magas entrópiájú formában (7.7. ábra). A Nap azt teszi értünk, hogy az alacsony entrópia hatalmas forrását biztosítja. Mi (a növények ügyessége révén) ebből húzunk hasznot, kivonjuk egy kis részét ennek az alacsony entrópiának, és átalakítjuk azzá a figyelemre méltó és bonyolultan szervezett szerkezetté, amely magunk vagyunk.
Lássuk még egyszer általánosan, mi történik az energiával és entrópiával a Nap és a Föld között. A Nap a látható fény fotonjainak formájában bocsát ki energiát. Ennek egy részét a Föld elnyeli, majd infravörös fotonok formájában visszasugározza. A látható és az infravörös fotonok között az a lényeges különbség, hogy az előbbiek frekvenciája, és ezért az egyes fotonok energiája nagyobb. (Emlékezzünk a 6. fejezetben megadott E = hv Planck-képletre! Ez azt mondja nekünk, hogy minél nagyobb egy foton frekvenciája, annál nagyobb az energiája.) Minthogy a látható fény egyes fotonjainak energiája nagyobb, mint az infravörös fotonoké, ezért kevesebb látható foton éri a Földet, mint amennyi infravörös elhagyja, a bejövő és távozó energia éppen egyensúlyban van. A Föld által az űrbe visszaköpött energia sokkal több szabadsági fok között oszlik meg, mint az, amelyet a Föld a Napból felvesz. Minthogy oly sokkal több szabadsági fok vesz részt az energia visszaküldésében, ezért a fázistér térfogata sokkal nagyobb, az entrópia roppant mértékben felnő. A zöld növények az energiát alacsony entrópiájú formában (viszonylag kevés látható fotont) felvéve és nagy entrópiájú formában (viszonylag sok infravörös fotont) visszasugározva képesek ezzel az alacsony entrópiával táplálkozni, és elvégzik a számunkra szükséges oxigén–szén szétválasztást.
Mindezt az teszi lehetővé, hogy a Nap egy forró pont az égen! Az égbolt nincs hőmérsékleti egyensúlyban: egy kis tartománya, nevezetesen a Nap által elfoglalt rész sokkal nagyobb hőmérsékletű, mint a többi. Ez a körülmény szolgáltatja nekünk az alacsony entrópia áhított hatalmas forrását. A Föld e forró pontból alacsony entrópiájú formában kapja az energiát (kevés fotont), és magas entrópiájú formában sugározza vissza azt (sok fotont) a hideg tartományokba.
Miért ilyen forró pont a Nap? Hogyan volt képes elérni ezt a hőmérsékleti egyensúlytól távoli, ezáltal alacsony entrópiájú állapotot? A válasz az, hogy a gravitációs összehúzódás hozta létre egy előzőleg egyenletesen eloszlott gázból (főként hidrogénből). Ahogy kialakulásának korai szakaszában összehúzódott, felmelegedett. Ezt folyamatosan csinálta, és amikor hőmérséklete és nyomása elért egy bizonyos pontot, akkor a gravitációs összehúzódás mellett talált egy másik energiaforrást, a termonukleáris reakciókat: a hidrogénmagok héliummagokká történő, energiát szolgáltató fúzióját. Termonukleáris reakciók nélkül a Nap sokkal forróbb és kisebb lett volna, mint amilyen ma, majd végül meghalt volna. A termonukleáris reakciók megállították a további összehúzódást, ezzel megakadályozták, hogy túlságosan forró legyen, és olyan hőmérsékleten stabilizálták, amely számunkra nagyon megfelel. Így sokkal tovább képes folyamatosan sugározni, mint egyébként tudott volna.
Fontos felismerni, hogy bár a termonukleáris reakciók kétségtelenül nagy jelentőségűek a Napból kisugárzott energia természetének és mennyiségének meghatározásában, a döntő a gravitáció. (A termonukleáris reakciók lehetősége nagyon komolyan hozzájárul a Nap entrópiájának alacsonyságához, de a fúzió entrópiájával összefüggő kérdések kényesek, és teljes tárgyalásuk csak bonyolítaná a gondolatmenetet anélkül, hogy befolyásolná a végső következtetést.)139 Gravitáció nélkül a Nap nem is létezne! Termonukleáris reakciók nélkül még sütne – noha számunkra nem megfelelő módon –, de sugárzó Nap egyáltalán nem lehetne gravitáció nélkül, ez szükséges az anyag egybentartásához és a kellő hőmérséklet és nyomás létrehozásához. Gravitáció nélkül a Nap helyén csak hideg és szétszóródó gáz volna, nem volna forró pont az égen!
Nem beszéltem még a földi „fosszilis tüzelőanyagok” alacsony entrópiájának forrásáról, de a meggondolások alapvetően ugyanazok. A hagyományos elmélet szerint a földben minden olaj (és földgáz) a történelem előtti növényi életből származik. Ismét a növények az alacsony entrópia forrásai. A történelem előtti növények alacsony entrópiájukat a Naptól kapták – tehát megint a diffúz gázból napot formáló gravitációs hatáshoz kell fordulnunk. Thomas Goldnak van egy érdekes, „különc” elmélete a földi olaj eredetére, amely vitatja e hagyományos nézetet. Azt állítja, hogy a földben sokkal több olaj van annál, mint amennyi a növényekből keletkezhetett. Gold úgy véli, hogy az olaj a Föld keletkezésekor záródott be annak belsejébe, és azóta folyamatosan szivárog ki a föld alatti zsebekbe.140 Elmélete szerint az olaj még a Föld keletkezése előtt szintetizálódott kint az űrben a napfény hatására. Tehát megint a gravitáció által kialakított Nap volna a felelős.
Mi a helyzet az atomerőművekben használt, az urán-235 izotópban rejlő nukleáris energiával? Az urán nem a Napból jött (bár egy szakaszban keresztül is mehetett a Napon), hanem más csillagokból, amelyek sok milliárd évvel ezelőtt robbantak fel szupernóva-robbanásokban! Az anyag valójában sok ilyen felrobbanó csillagból gyűlt össze. A robbanás kihányta az űrbe, és egy része végül (a Nap közvetítésével) összegyűlt, így kerültek a földbe a nehéz elemek, velük az összes urán-235. Minden egyes, alacsony entrópiás energiakészlettel rendelkező atommag heves magfolyamatokból származik, amelyek a szupernóva-robbanásokban mentek végbe. A robbanások olyan csillagok gravitációs összehúzódásainak141 eredményeképpen következtek be, amelyek tömege túl nagy volt ahhoz, hogy a termikus nyomóerők révén fenn tudják magukat tartani. Az összehúzódás és az azt követő robbanás eredményeképpen egy kis mag maradt meg – valószínűleg a neutroncsillag néven ismert alakban (erről többet később!). A csillag egy diffúz gázködből húzódott össze gravitációsan, és eredeti anyagának nagy része, benne a mi urán-235-ösünk, visszadobódott az űrbe. Ám amiatt, hogy a gravitációs összehúzódás végül egy neutroncsillag-magot eredményezett, az entrópiában hatalmas csökkenés ment végbe. Végül is megint a gravitáció a felelős, ez alkalommal a diffúz gáz neutroncsillaggá történő (végül heves) kondenzációját okozta.
Úgy látszik, arra a következtetésre jutunk, hogy amit magunk körül találunk, az entrópia minden figyelemre méltó alacsonyságát – ezáltal a második főtétel legrejtélyesebb vonását – annak a körülménynek kell tulajdonítanunk, hogy hatalmas mennyiségű entrópia nyerhető a diffúz gáz csillaggá való gravitációs összehúzódása révén. Honnan van ez az egész diffúz gáz? A helyzet az, hogy ez a gáz diffúzan indul, ezáltal hatalmas alacsony entrópiakészlettel lát el bennünket. Most is ebből a készletből élünk, és még sokáig ebből fogunk élni. A gáz gravitációs csomósodásának lehetősége adta nekünk a második főtételt. Mi több, nem pont a második főtétel az, amit e gravitációs csomósodás produkál, hanem valami sokkal pontosabb és részletesebb, mint az egyszerű állítás: „a világ entrópiája nagyon alacsonyról indult”. Az entrópia sok más különböző módon is lehetett volna ilyen „alacsony”, azaz lehetett volna nagyfokú „látható rend” a korai univerzumban, de egészen másféle, mint az a „rend”, amelyet ténylegesen megkaptunk. (Képzeljük el, hogy a korai világegyetem egy szabályos dodekaéder volt – ami nagyon tetszett volna Platónnak –, vagy valami más valószínűtlen alakzat. Ez valóban „látható rend”, de nem az a fajta, amelyet a valódi korai univerzumban várunk!) Meg kell értenünk, honnan van ez az egész diffúz gáz – és ezért a kozmologikus elméletekhez kell fordulnunk.
139 A csillagokban a könnyű magok (például hidrogén) nehezebbekké (például héliummá, vagy végül vassá) való egyesülése entrópianyereséggel jár. Eszerint a Földön jelen lévő hidrogénben sok „alacsony entrópia” van, amelynek egy részét végül hasznosíthatjuk a „fúziós” erőművekben a hidrogén héliummá való átalakításával. Az entrópianyerés e módja azért lehetséges, mert a gravitáció képessé teszi az atommagokat arra, hogy összesűrűsödjenek, távol a sokkal nagyobb számú fotontól, amelyek kiszöktek a tér rengetegébe, és most a 2,7 K fokos feketetest-háttérsugárzást alkotják. Ez a sugárzás sokkal-sokkal nagyobb entrópiát képvisel, mint amennyi a közönséges csillagokban az anyagban jelen van, és ha mindez visszasűrűsödne a csillagok anyagába, akkor a nehezebb magok legtöbbje megint szétesne alkotórészeire! A fúzió entrópianyeresége ezért „időleges”, és kizárólag a gravitáció sűrítő hatásának köszönhető. Később látni fogjuk, hogy noha a magfúzió útján elérhető entrópia nagyon nagy ahhoz képest, amit eddig a gravitáció közvetlenül termelt – és a feketetest-háttérsugárzás entrópiája még sokkal nagyobb annál – a dolgok ilyen állása tisztán lokális és időleges. A gravitáció entrópiaforrásai sokkal hatalmasabbak, mint akár a fúzióé, akár a 2,7 K fokos sugárzásé!
140 Svédországi ultramély fúrásokból származó új eredményeket lehet Gold elmélete alátámasztásaként értelmezni, ám a dolog eléggé vitatott, vannak más, hagyományos magyarázatok is.
141 Feltételezem, hogy ez az, amit „II típusú” szupernóvának neveznek. Ha „I típusú” volna, akkor megint a fúzió által szolgáltatott „átmeneti” entrópianyereségben gondolkozhatnánk (vö. 139. jegyzet). Ám nem valószínű, hogy az I típusú szupernóvák sok uránt termelnének.
Kozmológia és az ősrobbanás
Amennyire legnagyobb optikai és rádióteleszkópjaink elárulják nekünk, a világegyetem nagyon nagy skálán igen egyenletesnek látszik; de ami még figyelemreméltóbb, tágul. Minél messzebbre nézünk benne, az ottani galaxisok (és a még távolibb kvazárok) annál gyorsabban távolodnak tőlünk. Úgy tűnik, mintha az egész világegyetem egy gigantikus robbanásban keletkezett volna – ezt az eseményt nevezik ősrobbanásnak, amely néhányszor tízmilliárd évvel ezelőtt következett be.142 Meggyőzően támogatja az egyenletes eloszlást és az ősrobbanást a feketetest-háttérsugárzás megfigyelése. Ez 2,7° abszolút hőmérsékletnek (2,7 K), azaz –270,3 °C-nak megfelelő hőmérsékleti sugárzás. E hőmérséklet nagyon alacsonynak tetszhet – és valóban az is! –, ám magának a Nagy Robbanás pillanatának a maradványa! Minthogy a világegyetem azóta olyan hatalmas számszorosára tágult, e kezdeti tűzgolyó is ilyen hatalmas számszorosára oszlott szét. A hőmérséklet a Nagy Robbanásban messze felülmúlt minden ma elképzelhető hőmérsékletet, de a tágulás következtében lehűlt a feketetest háttérsugárzás mai parányi értékére. E háttérsugárzás jelenlétét a ma szabványos ősrobbanáskép alapján 1948-ban megjósolta George Gamow, orosz-amerikai fizikus és csillagász. Először (véletlenül) Penzias és Wilson figyelte meg 1965-ben.
E felfúvódó léggömb egészen jó képét adja a világegyetem három szabványos, ún. Friedmann–Robertson–Walker- (FRW-) modellje egyikének – a térben zárt, pozitív görbületű FRW-modellnek. A másik két (zérus vagy negatív görbületű) FRW-modellben a világegyetem ugyanígy tágul, de a térben nem véges, ahogy azt a léggömb ábrázolja, hanem végtelen, és a galaxisok száma is az.
E két végtelen modell közül a könnyebben felfogható a zérus görbületű, azaz euklideszi tér geometriája. Gondoljuk azt, hogy egy közönséges sima sík ábrázolja a teljes térbeli világegyetemet, a síkon megjelölt pontok a galaxisokat. Amint a világegyetem fejlődik az időben, e galaxisok egyenletesen távolodnak egymástól. Képzeljük most el a téridő képet. Eszerint minden „időpillanatban” egy külön euklideszi síkunk van, mindezeket egymás fölé rétegezve képzeljük, így a teljes téridőről egyszerre van képünk (7.9. ábra). A galaxisokat most görbék ábrázolják – a galaxisok történeteinek világvonalai – ezek a görbék a jövő irányában egymástól távolodnak. Ismét nincs kitüntetett galaxis-világvonal.
A harmadik, negatív görbületű FRW-modellben a térbeli geometria a nem-euklideszi, Bolyai–Lobacsevszkij-féle geometria, amelyet az 5. fejezetben írtunk le és Escher grafikájával szemléltettünk az 5.2. ábrán. A téridőleíráshoz minden „időpillanatban” egy ilyen Bolyai–Lobacsevszkij-féle térre van szükségünk, ezeket rétegezzük egymásra, hogy megkapjuk a teljes téridőképet (7.10. ábra).143 A galaxisok világvonalai most is a jövő irányában egymástól távolodó görbék, és nincs kitüntetett galaxis.
Mind e leírásokban természetesen a három térbeli dimenzióból egyet elhagytunk (ugyanúgy, mint az 5. fejezetben), az így kapott háromdimenziós téridő szemléletesebb, mint a teljes, négydimenziós. A pozitív görbületű téridőt még így is nehéz megjeleníteni, ha nem dobunk el még egy térbeli dimenziót! Tegyünk így, és ábrázoljuk ezt a térben zárt világegyetemet a léggömb (kétdimenziós) gömbfelülete helyett egy (egydimenziós) körrel. Ahogy a világegyetem tágul, úgy nő e kör mérete, a téridőt úgy ábrázolhatjuk, hogy ezeket a köröket rétegezzük egymásra (minden „időpillanatból” egy kört), így egy görbült kúpot kapunk [7.11. ábra (a) jelű része]. Einstein általános relativitáselméletének egyenleteiből következik, hogy e pozitívan zárt világegyetem nem tágulhat örökké. Miután elér egy maximális tágultságot, visszazsugorodik önmagába, végül egyfajta fordított ősrobbanásban mérete ismét nullává válik [7.11. ábra (b) jelű része]. Ezt az időfordított Nagy Robbanást olykor Nagy Roppanásnak nevezik. A világegyetem negatív és zérus görbületű (végtelen) FRW-modelljei nem zsugorodnak össze a fenti módon. A Nagy Roppanás helyett folytatják örökös tágulásukat.
Legalábbis ez igaz a szabványos általános relativitáselméletben, amelyben az ún. kozmológiai állandót nullának vesszük. Alkalmasan megválasztott nemzérus kozmológiai állandó mellett lehetséges olyan térben végtelen világegyetem-modell, amely összeesik egy nagy roppanásban, vagy véges, pozitív görbületű modellek, amelyek a végtelenségig tágulnak. Egy nemzérus kozmológiai állandó jelenléte kissé bonyolítaná a vizsgálatot, de céljaink szempontjából nem lényeges módon. Az egyszerűség kedvéért ezt az állandót nullának fogom venni.144 A könyv írásának idején a kozmológiai állandó a megfigyelések szerint nagyon kicsi, az adatok összhangban vannak azzal, hogy zérus. (További információra a kozmológiai modellekről lásd Rindler 1977.)
Az adatok sajnos még nem elég jók ahhoz, hogy világosan kiválasszák egyik vagy másik javasolt kozmológiai modellt (és hogy eldöntsék, lehet-e lényeges hatása egy kis kozmológiai állandónak). Első ránézésre azt sugallják, hogy a világegyetem térbelileg negatív görbületű (Bolyai–Lobacsevszkij-geometriával a nagy skálákon), és a tágulást a végtelenségig folytatja. Ez az állítás nagymértékben a látható formában jelen lévő anyag mennyiségére vonatkozó megfigyelésekre támaszkodik. Ám hatalmas mennyiségű láthatatlan anyag lehet szétszóródva az űrben, és ebben az esetben a világegyetem pozitív görbületű lehet, és végül majd összeeshet egy Nagy Roppanásban – igaz, hogy sokkal nagyobb idő múlva, mint a létrejötte óta eltelt nagyjából 1010 év. Az összeroppanás akkor lehetséges, ha mintegy harmincszor több anyag van szétszóródva az űrben ebben a láthatatlan formában – ez az ún. „sötét anyag” –, mint amennyit a teleszkópok közvetlenül elárulnak. Jó közvetett bizonyítékok vannak arra, hogy valóban jelentős mennyiségű sötét anyag van jelen, ám hogy elegendő-e „a világegyetem bezárására” (vagy térbeli kisimítására) – és összeroppantására –, az teljesen nyitott kérdés.
142 E szám értékén ma is vitatkoznak, a 6 · 109 év és az 1,5 · 1010 év közé teszik. Ezek az értékek jelentősen nagyobbak annál a 109 évnél, amely Edwin Hubble 1930 körüli első megfigyelései alapján elfogadhatónak látszott.
143 A zérus és negatív térgörbületű modellekre mint végtelen modellekre hivatkoztam. Vannak azonban módjai az ilyen modellek „bezárásának”, térben végessé tételének. Ez a megfontolás – amely nem valószínű, hogy lényeges a tényleges világegyetem szempontjából – nem nagyon befolyásolja a dolgokat, ezért nem javaslom, hogy aggodalmaskodjunk miatta.
144 Einstein 1917-ben vezette be a kozmológiai állandót, de 1931-ben megint kidobta az elméletből, úgy utalva korábbi bevezetésére, mint „legnagyobb tévedésére”!
Az ősi tűzgolyó
Keressük tovább a termodinamika második főtételének eredetét. Nyomon követtük addig, hogy jelen volt a diffúz gáz, amelyből a csillagok kondenzálódtak. Mi ez a gáz? Honnan származik? Főként hidrogénből áll, de tartalmaz kb. 23 (tömeg)százaléknyi héliumot, és kis mennyiségben más anyagokat is. A szabványos elmélet szerint ezt a gázt a világegyetemet létrehozó Nagy Robbanás köpte ki. Fontos azonban, hogy erre ne mint valami közönséges, megszokott robbanásra gondoljunk, amelyben az anyag egy középső pontból kerül ki a már korábban is létező térbe. Itt a tér maga is a robbanásban keletkezik, és nincs, vagy nem volt középső pont! A helyzet legkönnyebben talán a pozitív görbületű esetnél szemléltethető. Nézzünk rá újra a 7.11. ábrára vagy a 7.8. ábra felfúvódó léggömbjére. Nincs „előre létező üres tér”, amelybe a robbanás beömlesztené az anyagot. Maga a tér is, azaz a „léggömb felülete”, a robbanásban születik. Fel kell fognunk, hogy képeinken, a pozitív görbületű esetben, csak szemléltetési célokból használtuk a „környező teret” – az euklideszit, amelyben a léggömb ül, vagy azt a háromdimenziósat, amelyben a 7.11. ábra téridejét megrajzoltuk –, e környező tereket nem szabad fizikailag valóságosaknak vennünk. A léggömbön belül vagy kívül lévő tér csak a felület szemléltetését segíti. A világegyetem fizikai terét egyedül a léggömb felülete ábrázolja. Látjuk most, hogy nincs középső pont, amelyből az anyag a Nagy Robbanásban kirepül. A léggömb közepének látszó „pont” nem része a világegyetemnek, csupán a modell szemléltetését segíti elő. Az ősrobbanásban kizúduló anyag egyenletesen oszlik szét a teljes térbeli világegyetemben!
A helyzet a másik két szabványos modellben is ugyanez (csak talán egy kissé nehezebben képzelhető el). Az anyag soha nem tömörült össze a tér egyetlen pontjában. Egyenletesen töltötte be az egész teret a kezdet kezdetétől fogva!
Ez a kép az alapja a standard modellként idézett forró ősrobbanás elméletének. Eszerint a világegyetem pillanatokkal születése után rendkívül forró hőmérsékleti állapotban volt – ez volt az ősi tűzgolyó. Részletes számításokat végeztek a tűzgolyó kezdeti összetevőinek arányaira és természetére vonatkozóan, és hogy hogyan változtak ezek az összetevők, amint a tűzgolyó (a teljes világegyetem) tágult és hűlt. Figyelemre méltó lehet, hogy megbízható számítások végezhetők a világegyetem egy, a jelenlegitől annyira különböző állapotának leírására. Ám a fizika, amelyen e számítások alapulnak, egyértelmű, amíg nem kérdezzük meg, mi történt a születés utáni másodperc első 10–4 része előtt! Attól az egytízezred másodperctől a születés utáni kb. harmadik percig a történteket nagy részletességgel kidolgozták (vö. Weinberg 1977) – és a világegyetem mai, nagyon különböző állapotának kísérleti megismerése alapján leszármaztatott, jól megalapozott fizikai elméleteink, figyelemre méltóan, erre teljesen alkalmasak.145 E számítások végső következtetései szerint a teljes világegyetemben egyenletesen oszlik el sok foton (azaz fény), elektron és proton (a hidrogénatom két alkotórésze), valamennyi α-részecske (a hélium atommagja), még kevesebb deuteron (a hidrogén egyik nehéz izotópjának, a deuteriumnak az atommagja), és nyomokban más atommagok – esetleg együtt nagyszámú „láthatatlan” részecskével, például neutrínókkal, amelyek alig adnak hírt magukról. Az anyagi alkotórészek (főként a protonok és az elektronok) állnak majd össze, hogy létrehozzák azt a gázt (főként hidrogént), amelyből a csillagok alakulnak ki, kb. 108 évvel az ősrobbanás után.
Megmagyarázza-e az ősrobbanás a második főtételt?
Véget ér-e itt kutatásunk? A rejtélyes ténynek, hogy világegyetemünk entrópiája olyan alacsonyról indult – amiből a termodinamika második főtételét kaptuk –, az-e a „magyarázata”, hogy a világegyetem egy Nagy Robbanásban született? Kis töprengés után arra jutunk, hogy van valami paradox ebben az elképzelésben. A válasz nem lehet igazán ez. Emlékezzünk rá, hogy az ősi tűzgolyó hőmérsékleti állapot volt – forró gáz táguló hőmérsékleti egyensúlyban. Ne felejtsük el, hogy a „hőmérsékleti egyensúly” kifejezés a maximális entrópiájú állapotra vonatkozik. (Így neveztük a dobozba zárt gáz maximális entrópiájú állapotát.) Ám a második főtétel azt követeli meg, hogy kezdeti állapotában világegyetemünk entrópiája valahogy minimális volt, nem maximális!
Mit rontottunk el? Egy „szabvány” válasz durván a következő lehetne:
Igaz, a tűzgolyó kezdetben lényegében hőmérsékleti egyensúlyban volt, de a világegyetem akkor nagyon kicsi volt. A tűzgolyó az olyan kisméretű univerzum számára megengedhető maximális entrópiájú állapotot képviselte, de ez az entrópia parányi lehetett a mai méretű világegyeteméhez képest. A tágulás során a megengedett maximális entrópia a világegyetem méretével növekedett, de a világegyetem tényleges entrópiája jóval elmaradt e megengedett maximum mögött. A második főtétel azért jelenik meg, mert a tényleges entrópia mindig a megengedett maximumot igyekszik utolérni.
Rövid megfontolás után azonban arra jutunk, hogy ez nem lehet a helyes magyarázat. Ha az volna, akkor egy (térben zárt) univerzummodell esetében, amely végül összeesik egy nagy roppanásban, az érvelés elmondható volna a megfordított időirányban. Amikor az univerzum végül parányi méretűre zsugorodik, akkor az entrópia lehetséges értékeinek ismét alacsony maximuma lesz. Ugyanaz a megszorítás, amely a táguló világegyetem nagyon korai szakaszaiban az alacsony entrópiát adta, az összehúzódó világegyetem végső szakaszaiban ismét alkalmazható volna. Ez „az idő kezdetére” vonatkozó alacsonyentrópiás kényszer adta a második főtételt, amely szerint a világegyetem entrópiája időben növekszik. Ha ugyanezt a kényszert „az idő végére” alkalmaznánk, akkor nagy ellentmondásba kerülnénk a termodinamika második főtételével!
Az természetesen nyugodtan előfordulhat, hogy valóságos világegyetemünk soha nem esik össze ezen a módon. Esetleg egy zérus általános térgörbületű világegyetemben élünk (euklideszi eset) vagy negatív görbületűben (Bolyai–Lobacsevszkij-féle eset). Vagy talán (pozitív görbületű) újra összeesőben, de az összeesés olyan távoli időben következik be, hogy jelen korszakunkban a második főtétel semmiféle sértése nem ismerhető fel – annak a ténynek ellenére, hogy e nézőpont szerint a világegyetem teljes entrópiája végül majd megfordul és egy parányi értékre csökken – és a második főtétel, a ma ismert formájában, durván megsérül.
Ténylegesen nagyon jó okunk van kételkedni abban, hogy egy zsugorodó világegyetemben az entrópia változása így megfordulhat. A legerősebb érvek a fekete lyukak néven ismert titokzatos objektumokhoz kapcsolódnak. Egy fekete lyukban a zsugorodó univerzum egy mikrokozmoszát találjuk; így ha az entrópia a zsugorodó univerzumban valóban megfordulna, akkor egy fekete lyuk környezetében a második főtétel komolyan meg kellene sérüljön. Azonban minden okunk megvan, hogy azt higgyük, a második főtétel diadalmasan uralkodik a fekete lyukaknál is. A fekete lyukak elmélete alapvetően hozzájárul az entrópiáról folytatott vizsgálatunkhoz, ezért kissé részletesebben meg kell vizsgálnunk ezeket a különös objektumokat.
Fekete lyukak
Nézzük meg először, mit mond az elmélet Napunk végső sorsáról. A Nap úgy ötmilliárd éve létezik. Egy másik 5-6 milliárd éven belül elkezd majd tágulni, elkerülhetetlenül feldagad, felülete eléri nagyjából a Föld pályáját. Ekkor olyan típusú csillaggá változik, amelyet vörös óriás néven ismernek. Az égbolton sok vörös óriás figyelhető meg, a két legismertebb az Aldebaran a Taurus és a Betelgeuse az Orion csillagképben. Amíg felülete tágul, magjának legbelső részében egy kivételesen sűrű kis anyagcsomó jön létre, amely gyorsan növekszik. Ez a sűrű mag olyan természetű, mint egy fehér törpe csillag (7.12. ábra).
A fehér törpék, önmagukban, olyan valódi csillagok, amelyek sűrűsége rendkívül nagy, mintha egy pingponglabda anyaga néhány száz tonnát nyomna! Ilyen csillagokat is egészen nagy számban figyelnek meg az égen: Tejutunk fényes csillagainak talán tíz százaléka fehér törpe. A legnevezetesebb a Szíriusz társa, amelynek riasztóan nagy sűrűsége komoly rejtélyt jelentett a csillagászoknak századunk elején. Később azonban ugyanez a csillag csodálatosan megerősített egy fizikai elméletet (amelyet eredetileg R. H. Fowler dolgozott ki 1926 körül), mely szerint egyes csillagoknak valóban lehet ilyen nagy sűrűségük, ezeket a „degenerált elektronok nyomása”, azaz az elektronokra alkalmazott Pauli-féle kvantummechanikai kizárási elv menti meg a gravitációs kollapszustól.
Minden vörös óriásnak egy fehér törpe van a magjában, amely folyamatosan gyűjti az anyagot a csillag fő testéből. E parazita mag végül teljesen elfogyasztja a vörös óriást, és ami megmarad, az egy igazi – nagyjából a Földdel megegyező méretű – fehér törpe. Napunk várhatóan „csak” néhány milliárd évig létezik még, mint vörös óriás. Utána, utolsó „látható” megtestesülésében – mint egy fehér törpe lassan kihunyó parazsa146 – a Nap kitart még egy néhány milliárd évig, végül teljes sötétségbe burkolózik, mint egy láthatatlan fekete törpe.
Nem minden csillag osztozik a Nap sorsában. Egyesek lényegesen erőszakosabb véget érnek, sorsukat az ún. Chandrasekhar-korlát szabja meg: egy fehér törpe csillag tömegének maximális lehetséges értéke. Subrahmanyan Chandrasekhar egy 1929-ben elvégzett számítása szerint egy fehér törpének a tömege nem lehet nagyobb, mint a Nap tömegének nagyjából hatötöd része. (Fiatal indiai kutatójelölt volt, hajón utazott Indiából Angliába, ekkor végezte számítását.) A számítást tőle függetlenül megismételte 1930 táján az orosz Lev Landau. A Chandrasekhar-korlát mai, némileg finomított értéke kb.
1,4M⊙,
ahol M⊙ a Nap tömege.
Vegyük észre, hogy a Chandrasekhar-korlát nem sokkal nagyobb, mint a Nap tömege, míg sok közönséges csillagot ismerünk, amelyek tömege jelentősen nagyobb ennél az értéknél. Mi a végső sorsa például egy 2M⊙ tömegű csillagnak? Az elmélet szerint ez is vörös óriássá dagad fel, és fehér törpe magja lassacskán nyeli a tömeget, pont úgy, mint az előbb. Azonban egy kritikus ponton a mag tömege eléri a Chandrasekhar-korlátot, és ekkor Pauli kizárási elve elégtelennek bizonyul a hatalmas gravitációs nyomás ellensúlyozására.147 Ezen a ponton, vagy e körül, a mag katasztrofálisan összeomlik, a hőmérséklet és a nyomás óriási mértékben megnő. Heves magfolyamatok indulnak be, és a magból óriási mennyiségű energia szabadul fel neutrínók formájában. Ezek felmelegítik a csillag külső tartományát, amely egyre zuhan befelé, és egy elképesztő méretű robbanás következik be. A csillag szupernóvává válik!
Mi történik a még mindig összeeső magban? Az elmélet azt mondja, hogy még sokkal nagyobb sűrűségeket ér el, mint a fehér törpe belsejében már létrejött rémisztő értékek. A mag neutroncsillagként stabilizálódhat, amelyben most a degenerált neutronok nyomása – azaz a neutronokra alkalmazott Pauli-elv – ellensúlyozza a gravitációt. A sűrűség akkora, hogy a neutroncsillag anyagát tartalmazó pingponglabdánk olyan súlyú volna, mint a Hermesz kisbolygó (vagy esetleg a Mars holdja, a Démosz). Ez éppen az a fajta sűrűség, amely magában az atommagban található! (A neutroncsillag olyan, mint egy hatalmas atommag, sugara esetleg néhányszor tíz kilométer, amely azonban rendkívül kicsi a csillagméretekhez képest!) Van azonban egy, a Chandrasekharéhoz hasonló, új korlát (a Landau–Oppenheimer–Volkov-korlát), amelynek mai (javított) értéke nagyon durván
2,5M⊙,
efölött a neutroncsillag nem képes ellensúlyozni a gravitációt.
Mi történik az összeomló magban, ha az eredeti csillag tömege elég nagy, hogy még ezt a korlátot is felülmúlja? Sok csillagot ismernek, amelyek tömege például a 10M⊙ és 100M⊙ közötti tartományba esik. Nagyon valószínűtlennek látszik, hogy minden esetben ledobjanak annyi tömeget, hogy a kialakuló mag a neutroncsillag-korlát alá essen. A várakozás ehelyett az, hogy egy fekete lyuk alakul ki.
Mi az a fekete lyuk? A térnek – vagy a téridőnek – egy olyan tartománya, amelyen belül a gravitációs mező olyan erőssé vált, hogy még a fény sem tud kiszökni belőle. Emlékezzünk arra, a relativitási elvek egyik velejárója, hogy a fény sebessége határsebesség: anyagi objektum vagy jel sebessége nem múlhatja felül a lokális fénysebességet (5. fejezet). Így ha a fény nem képes kiszökni a fekete lyukból, akkor semmi sem.
Az Olvasó esetleg ismeri a szökési sebesség fogalmát. Az a sebesség ez, amelyet egy objektumnak el kell érnie, hogy megszökjék egy tömeges testről. Tegyük fel, hogy a test a Föld; az erről való szökési sebesség közelítőleg 40 000 kilométer óránként. A Föld felszínéről feldobott (a talajtól tetszőleges irányban távolodó) kő, ha sebessége felülmúlja ezt az értéket, véglegesen megszökik a Földről (feltéve, hogy elhanyagolhatjuk a légellenállás hatását). Ha ennél kisebb sebességgel dobjuk fel, akkor visszaesik a Földre. (Nem igaz tehát, hogy „minden, ami felmegy, vissza kell jöjjön”; egy objektum csak akkor tér vissza, ha a szökési sebességnél kisebb sebességgel dobták fel!) A Jupiteren a szökési sebesség 220 000 kilométer per óra; a Napon 2 200 000 kilométer óránként. Képzeljük most azt, hogy a Nap tömegét egy olyan gömbbe sűrítjük össze, amelynek sugara jelenlegi sugarának egynegyede, ekkor a jelenlegi értéknél kétszer nagyobb szökési sebességet kapunk; ha a Napot még jobban összesűrítenénk, mondjuk jelenlegi sugarát egyszázad részére, akkor a szökési sebesség tízszer nagyobb volna. Elképzelhető, hogy egy elég nagy tömegű és sűrűségű testnél a szökési sebesség még a fény sebességét is felülmúlhatja! Amikor ez bekövetkezik, akkor egy fekete lyukkal állunk szemben.148
A 7.13. ábrán egy test fekete lyukká való összeomlását téridődiagramon rajzoltam le. (Feltételeztem, a kollapszus úgy zajlik le, hogy a gömbszimmetria ésszerű közelítésben megmarad, és elhagytam egy térbeli dimenziót.) Feltüntettem a fénykúpokat, ahogy azt az általános relativitáselmélet 5. fejezetbeli tárgyalásából felidézhetjük (5. fejezet), ezek jelzik egy anyagi objektum vagy jel mozgásának abszolút korlátait. Vegyük észre, hogy a kúpok befelé, a középpont felé billennek, annál jobban, minél közelebb vannak a középponthoz.
Van egy, a középponttól számított k
ritikus távolság, a neve Schwarzschild-sugár, amelynél a kúpok külső határa az ábrán függőleges. Ennél a távolságnál a fény (amelynek a fénykúpokat kell követnie) egyszerűen lebeg az összeomló test fölött, legfeljebb olyan kifelé mutató sebességre tud szert tenni, amely éppen csak ellenáll a hatalmas gravitációs vonzásnak. E lebegő fény (azaz a fény teljes története) által a téridőben a Schwarzschild-sugárnál kirajzolt (hármas-) felületet a fekete lyuk (abszolút) eseményhorizontjának nevezik. Minden, ami az eseményhorizonton belül van, képtelen kiszökni vagy egyáltalán összeköttetésbe lépni a külső világgal. Ez látható a kúpok dőléséből és abból az alapvető tényből, hogy minden mozgás és jel csak e kúpokon belül terjedhet. Egy néhány naptömegű csillag kollapszusából kialakult fekete lyuknál a horizont sugara néhány kilométer. Sokkal nagyobb fekete lyukakat várunk a galaktikus középpontokban. A mi galaxisunkban, a Tejútrendszerben is lehet akár egymillió naptömegnyi fekete lyuk, ennek sugara néhány millió kilométer volna.
Maga az anyagi test, amely összeomolva fekete lyukat képez, teljesen a horizonton belül végzi be pályafutását, ezért képtelen kapcsolatba lépni a külvilággal. Hamarosan megtárgyaljuk a test valószínű sorsát. Egyelőre a kollapszus által létrehozott téridő-geometria érdekel bennünket – amelynek igen furcsa tulajdonságai vannak.
Képzeljünk el egy bátor (vagy vakmerő?) B űrhajóst, aki elhatározza, hogy meglátogat egy nagy fekete lyukat, míg félénkebb (vagy óvatosabb) társa, A biztonságosan kívül marad az eseményhorizonton. Tételezzük fel, hogy A, ameddig csak lehet, igyekszik szemmel tartani B-t. Mit lát A? A 7.13. ábráról kideríthetjük, hogy B történetének (azaz B világvonalának) az a része, amely a horizonton belül fekszik, soha nem lesz látható A számára, míg a horizonton kívül fekvő rész végül igen – noha B-nek a horizonton való eltűnését közvetlenül megelőző pillanatait A csak mind hosszabb és hosszabb várakozások után látja meg. Tegyük fel, hogy B akkor keresztezi a horizontot, mikor saját órája 12-t mutat. Ennek az eseménynek A soha nem lesz tanúja, de a 11:30, 11:45, 11:52, 11:56, 11:58, 11:59, 11:59 1/2, 11:59 3/4, 11:59 7/8 stb. óraállások leolvasásait egymást követően látni fogja (az ő megítélése szerint nagyjából azonos időközökben). Elvileg B mindig látható marad A számára, örökké a horizont felett fog lebegni, órája mind lassabban fog közelíteni a végzetes 12:00 órához, de sohasem fogja elérni azt. Ténylegesen azonban B képe, amelyet A felfog, nagyon gyorsan túl homályossá és így felismerhetetlenné válik. Ennek oka az, hogy a fény B világvonalának kicsiny, még éppen a horizonton kívüli részéről kell kitöltse az A által észlelt idő egész maradékát. B valójában eltűnik A szeme elől – és ugyanez volna igaz az egész eredeti összeomló testre. Minden, amit A láthat, az valójában éppen egy „fekete lyuk”!
Mi a helyzet szegény B-vel? Mit fog ő tapasztalni? Először arra kell rámutatnunk, hogy semmiképpen nem fogja észrevenni azt a pillanatot, amikor keresztezi a horizontot. Rápillant órájára 12 körül, és látja, hogy a percek szabályosan mennek: 11:57, 11:58, 11:59, 12:00, 12:01, 12:02, 12:03, … . Semmi rendkívüli nem látszik a 12:00 időpont körül. Visszanézhet A-ra, azt látja, hogy A az egész idő alatt a látóterében marad. Ránézhet A órájára, s rendes, szabályos módon látja azt előre haladni. Ha B nem számította ki, hogy kereszteznie kell a horizontot, akkor más módon nem szerezhet tudomást róla.149 A horizont nagyon ravaszul viselkedik. Ha egyszer B átlépte, akkor többé nem menekülhet. Az őt környező világegyetem végül összeomlik körülötte, hamarosan utoléri saját magánjellegű „nagy roppanása”.
Vagy talán nem is annyira magánjellegű ez. A fekete lyukat létrehozó összeeső test minden anyagának „ugyanaz” a roppanás lesz a sorsa. Ha a világegyetem a lyukon kívül térben zárt, és így végül a külső anyagot is elnyeli egy mindent magába olvasztó nagy roppanás, akkor ezt „ugyanolyannak” várjuk, mint B „magánroppanását”.150
B nem kellemes sorsa ellenére nem várjuk azt, hogy az általa addig tapasztalt lokális fizika hadilábon álljon azzal, amit megismertünk és megértettünk. Nem várjuk, hogy a termodinamika második főtételének megsértését tapasztalja, nem is beszélve az entrópia növekedésének teljes megfordulásáról. A második főtétel a fekete lyukon belül éppúgy érvényben marad, mint máshol. Az entrópia B környezetében is növekszik a végső összeroppanás pillanatáig.
Hogy megértsük, hogyan lehet az entrópia egy (akár „magán”, akár „mindent beborító”) Nagy Roppanásban óriási nagy, noha a Nagy Robbanásban sokkal alacsonyabbnak kellett lennie, egy kicsit mélyebbre kell ásnunk a fekete lyuk téridő-geometriájában. Mielőtt azonban ezt tennénk, vessen az Olvasó egy pillantást a 7.14. ábrára is, amely egy fekete lyuk hipotetikus időmegfordítottját mutatja, nevezetesen egy fehér lyukat. Fehér lyukak valószínűleg nem léteznek a természetben, de elméleti lehetőségüknek lényeges jelentősége lesz számunkra.
146 Életének utolsó szakaszában a törpe úgy parázslik, mint egy vörös csillag – de amit „vörös törpének” neveznek, az egészen más jellegű csillag!
147 A Pauli-elv azt nem tiltja meg, hogy az elektronok azonos „helyen” legyenek, de azt igen, hogy két elektron ugyanolyan „állapotban” legyen – beleértve azt is, hogyan mozognak és pörögnek. A tényleges bizonyítás kis finomságokat is tartalmaz; mikor először közzétették, sokan vitatták, különösen Eddington.
148 E gondolatmenetet már 1784-ben kidolgozta az angol csillagász, John Michell, és valamivel később tőle függetlenül Laplace. Arra a következtetésre jutottak, hogy a világegyetemben a legnagyobb tömegű és legsűrűbb testek – mint a fekete lyukak – valóban teljesen láthatatlanok lehetnek, de (bizonyára profetikus) érvelésüket a newtoni elméletre alapozták, amelyben ezek a következtetések a legjobb esetben is vitathatók. Megfelelő általános relativisztikus levezetést először John Robert Oppenheimer és Hartland Snyder adtak (1939).
149 Általános, nem stacionárius fekete lyuk esetében a horizont egzakt helyzete közvetlen méréssel nem határozható meg. Részben attól függ, hogy mennyi anyag fog a jövőben összesen a lyukba esni!
150 Ez az állítás két feltételezést tartalmaz. Az első az, hogy a fekete lyuk lehetséges végső eltűnését – a Hawking-sugárzás hatására bekövetkező (rendkívül lassú) „elpárolgást”, amiről később szó lesz – előre jelzi az univerzum kollapszusa; a második egy (nagyon ésszerű) feltevés, amely „kozmikus cenzúra” néven ismert (5. fejezet).
Pauli alakja volt az aki leginkább megfogott Heisenberg könyvében. Pauli végső lelkesedése, hogy közelébe jutott egy addig megválaszolatlan valaminek, és erről szárnyaló levelekben tudósítja barátját, aztán az elhallgatása (hogy mégsem sikerült), majd a halála.
…
1974-ben vagy 73-ban lehetett, Szentgyörgyi Albert előadása a Gólyavárban. Hatalmas hangja és előadásának, személyiségének izzó energiája betöltötte a zsúfolt nagyelőadót. Azt hiszem bőven annyi idős lehetett ekkor, mint Paoli volt ama lelkesült időszakában.
Szentgyörgyi arról beszélt előadása vége felé, hogy figyelme most az elektronok felé fordult. Azokkal foglalkozik, mert azok alapvető jelentőségűek világunkban…
A téridő-szingularitások szerkezete
Idézzük fel az 5. fejezetből, hogyan nyilvánul meg a téridő görbülete az árapályjelenségben. Egy nagy test gravitációs mezőjében szabadon eső részecskék által alkotott gömbfelület az egyik irányban (a vonzó test irányában) megnyúlik, az erre merőleges irányban összenyomódik. Ez az árapálytorzulás a vonzó test felé haladva nő (7.15. ábra), fordítottan arányos a távolság köbével. Ilyen növekvő árapályhatást érez a B űrhajós, amint a fekete lyuk felé esik. Egy néhány naptömegű fekete lyuknál ez az árapályhatás óriási – messze erősebb annál, semhogy az űrhajós túlélhesse a lyuk megközelítését, a horizont átlépéséről nem is beszélve. Nagyobb lyukaknál az árapályhatás mértéke a horizontnál ténylegesen kisebb. A millió naptömegű fekete lyuknál, amely sok csillagász hiedelme szerint ott ülhet galaxisunk, a Tejút központjában, a horizont keresztezésekor egész kicsi az árapályhatás, bár ahhoz valószínűleg elegendő, hogy az űrhajós egy kicsit kényelmetlenül érezze magát. Nem marad azonban sokáig kicsi, amint az űrhajós bekerül a lyukba: néhány másodperc alatt végtelen nagyra nő fel! E gyorsan növekvő árapályhatás nem csak darabokra tépné űrhajósunk testét, de gyors egymásutánban ezt tenné magukkal a testet felépítő molekulákkal, azok atomjaival, atommagjaival, végül az összes szubatomi részecskével is! A „roppanás” így végzi utolsó pusztítását.
Nemcsak minden anyag semmisül meg ezen a módon, hanem maga a téridő is! E végső katasztrófa a téridő-szingularitás nevet viseli. Az Olvasó joggal kérdheti, miből tudjuk, hogy ilyen katasztrófák be kell következzenek, és milyen körülmények között kell az anyagnak és a téridőnek elszenvednie ezt a sorsot. Mindezek az általános relativitáselmélet klasszikus egyenleteiből következnek, minden olyan esetben, amikor egy fekete lyuk képződik. Oppenheimer és Synder (1939) eredeti feketelyuk-modellje mutatta ezt a fajta viselkedést. Am az asztrofizikusok sokáig abban reménykedtek, hogy e szinguláris viselkedés a speciális szimmetriák következménye, amelyeket a modellben feltételezni kellett. Valós (aszimmetrikus) helyzetekben az összehúzódó anyag talán bonyolult módon örvénylik, és végül megint kiszökik. E remények azonban szertefoszlottak, amikor általánosabb matematikai bizonyítások születtek, amelyek az ún. szingularitástételeket szolgáltatták (vö. Penrose 1965, Hawking és Penrose 1970). E tételek kimondják, hogy a klasszikus általános relativitáselméleten belül, ésszerű anyagforrások mellett a gravitációs kollapszusokban a téridő-szingularitások elkerülhetetlenek.
Hasonlóképpen, a fordított időirányt használva, elkerülhetetlenül találunk egy megfelelő kezdeti téridő-szingularitást, amely táguló világegyetemben a Nagy Robbanást jelenti. Ez a szingularitás nem az anyag és a téridő megsemmisülését, hanem születését ábrázolja. Úgy tűnhet, hogy a szingularitások e két típusa között egzakt időbeli szimmetria van: a kezdeti típusúban a téridő és az anyag születik, a végső típusúban megsemmisül. A hasonlóság valóban lényeges e két helyzet között, ám részletes vizsgálatnál azt találjuk, hogy egyik a másiknak nem egzakt időmegfordítottja. A geometriai különbségeket fontos megértenünk, mert ezekben van a termodinamika második főtétele eredetének kulcsa!
Térjünk vissza önfeláldozó B űrhajósunk észleléseihez! Árapályerőkkel találkozik, amelyek gyorsan végtelen nagyra nőnek. Minthogy üres térben utazik, a térfogatmegőrző, de torzító hatásokat észleli, amelyeket a WEYL névvel ellátott típusú téridő-görbületi tenzor szolgáltatja (lásd 5. fejezet). A téridő görbületi tenzorának másik része, amely egy általános összenyomást képvisel, és amelyet a RICCI névvel jelöltem, üres térben zérus. Előfordulhat, hogy B anyaggal találkozik, de még ha ez is a helyzet (és végül ő maga is anyagból épül fel), akkor is általánosan igaz marad, hogy a WEYL mértéke sokkal nagyobb, mint a RICCI-é. Valójában azt várjuk, hogy egy végső szingularitáshoz közel a görbületet a WEYL tenzor lényegében meghatározza. Ez a tenzor általánosan a végtelenhez tart:
WEYL → ∞,
(bár ezt oszcillálva is teheti). Úgy látszik, hogy egy téridő-szingularitásnál ez az általános helyzet.151 Az ilyen viselkedés egy nagy entrópiájú szingularitáshoz kapcsolódik.
Egészen különbözőnek látszik azonban a helyzet a Nagy Robbanásnál. Ennek standard modelljeit a magas fokú szimmetriát mutató Friedmann–Robertson–Walker-téridők adják, amelyeket korábban áttekintettünk. Itt a WEYL tenzor okozta torzító árapályhatás teljesen hiányzik. Helyette szimmetrikus, befelé gyorsító erők hatnak a próbarészecskékből álló gömbfelületekre (lásd 5.26. ábra). Ez nem a WEYL tenzor hatása, hanem a RICCI tenzoré. Tetszőleges FRW-modellben mindig fennáll a
WEYL = 0
tenzoregyenlőség. Ahogy a kezdeti szingularitást egyre jobban megközelítjük, azt találjuk, hogy most a WEYL helyett a RICCI tenzor válik végtelenné:
RICCI → ∞,
a kezdeti szingularitás közelében ez dominál. Ez alacsony entrópiájú szingularitást hoz létre.
Ha megvizsgáljuk a Nagy Roppanás-szingularitást az egzakt, összeomló FRW-modellekben, akkor azt találjuk, hogy a roppanásnál WEYL = 0, míg RICCI a végtelenhez tart. Ám ez egy nagyon speciális helyzet, és nem az, amit egy teljesen realisztikus modelltől várunk, amely a gravitációs csomósodást is figyelembe veszi. Az idő haladtával az eredetileg diffúz gáz formájú anyag csillagok galaxisaiba csomósodik össze. Kellő időben sok csillag gravitációsan összehúzódik: fehér törpékbe, neutroncsillagokba és fekete lyukakba, a galaktikus középpontokban hatalmas fekete lyukak lehetnek. A csomósodás – különösen a fekete lyukak esetében – hatalmas entrópianövekedéssel jár együtt (lásd 7.16. ábra). Első hallásra rejtélyes lehet, hogy a csomós állapotok nagy entrópiát képviselnek, a simák alacsonyat, főleg ha arra emlékezünk, hogy a dobozba zárt gázban a csomós állapot (amikor az egész gáz a doboz egyik sarkában van) volt az alacsony, a hőmérsékleti egyensúly egyenletes állapota pedig a magas entrópiájú. Amikor a gravitációt figyelembe vesszük, akkor a gravitációs mező egyetemleges vonzó természete következtében az egész megfordul. A csomósodás az idő haladtával egyre erősödik, végül sok fekete lyuk olvad össze, szingularitásaik az igen bonyolult végső Nagy Roppanás-szingularitásban egyesülnek. A végső szingularitás egyáltalán nem emlékeztet az összeomló FRW-modell idealizált Nagy Roppanására, amelyeknél WEYL = 0. Minél erősebb a csomósodás, az egész idő alatt annál inkább nagy lesz a Weyl-tenzor152, és általában minden végső szingularitásnál WEYL → ∞. A 7.17. ábra téridőképe egy zárt világegyetem teljes történetét ábrázolja a fenti általános leírással összhangban.
Látjuk most, miért nem kell kis entrópiájának lennie egy összeomló világegyetemnek. Az entrópia „alacsonysága” a Nagy Robbanásnál – ami a második főtételt adta nekünk – nem csupán a világegyetem „kicsiségének” volt következménye! Ha időben megfordítanánk a Nagy Roppanásról most kapott képet, akkor olyan „Nagy Robbanást” kapnánk, amelyben az entrópia borzasztóan magas, és nem volna második főtétel! Valamilyen okból a világegyetem egy nagyon speciális (alacsony entrópiájú) állapotban keletkezett, az FRW-modellek WEYL = 0 megszorítása valamilyen formában érvényesült. Ha ilyen természetű megszorítás nem volna, akkor „sokkal valószínűbb” lenne az a helyzet, amelyben mind a kezdeti, mind a végső szingularitások nagy entrópiájú, WEYL → ∞ típusúak lennének (lásd 7.18. ábra). Egy ilyen „valószínű” világegyetemben a termodinamikának nem volna második főtétele
151 Lásd Belinskii, Khalatnikov, Lifshitz (1970), valamint Penrose (1979b) vizsgálatait.
152 Egy rendszer entrópiájának gravitációs járulékát a teljes Weyl-görbület valamilyen mértékével igyekeztek azonosítani, de egyelőre nem találtak ilyet. (Általánosan eléggé rémes, nemlokális tulajdonságokra volna szükség.) Szerencsére a gravitációs entrópia ilyen mértékére a jelenlegi tárgyalásban nincs szükség.
!
Mennyire volt speciális a Nagy Robbanás?
Próbáljuk most megérteni, milyen erős kényszert jelentettek a Nagy Robbanásnál a WEYL = 0 típusú feltételek. Az egyszerűség kedvéért (ugyanúgy, mint az előbb) tételezzük fel, hogy a világegyetem zárt. Hogy határozott számokat tudjunk kihozni, feltételezzük, hogy a világegyetemben a barionok B száma – azaz a protonok és neutronok együttes száma – durván
B = 1080.
(Nincs különös oka annak, hogy pont ezt az értéket választottuk, legfeljebb az, hogy a megfigyelések szerint B-nek legalább ekkorának kell lennie; Eddington egyszer azt állította, hogy egzaktul kiszámította B-t, és a fentihez közeli értéket kapott! Ezt a számítást ma már senki sem hiszi el, de a 1080 érték, úgy látszik, megragadt.) Ha B-t ennél nagyobbra választanánk (esetleg B = ∞ az igazság), akkor a kapott számok még meglepőbbek volnának, mint azok az így is eléggé rendkívüliek, amelyekhez egy percen belül eljutunk!
Próbáljuk elképzelni a teljes világegyetem fázisterét! E fázistér minden egyes pontja különböző lehetséges kiindulási pontot ábrázol. Egy „tűvel” felfegyverkezett Teremtőt képzelünk el, aki kiválasztja a fázistér valamelyik pontját (7.19. ábra). A tű mindegyik különböző elhelyezése különböző világegyetemet hoz létre. A Teremtő céljainak megfelelő pontosság az így létrehozott világegyetem entrópiájától függ. Viszonylag „könnyű” volna nagy entrópiájú univerzumot teremteni, mert ekkor a tű a fázistér egy nagy térfogatába szúrhatna bele. (Emlékezzünk arra, hogy az entrópia a fázistér-térfogat logaritmusával arányos.) Ám hogy a világot alacsony entrópiájú állapotból indítsa – hogy valóban legyen egy második főtétel –, a Teremtőnek a fázistér egy sokkal kisebb térfogatába kell céloznia. Milyen kicsi legyen ez a tartomány, hogy az így létrejövő világegyetem közelről emlékeztessen arra, amelyben élünk? A kérdés megválaszolásához először Jacob Bekenstein (1972) és Stephen Hawking (1975) egy igen nevezetes képletéhez kell fordulnunk, amely megmondja, mi kell legyen egy fekete lyuk entrópiája.
kellene céloznia – a teljes térfogatnak kb.
részébe. (A tű és a megcélzott pont nem méretarányos.)
Tekintsünk egy fekete lyukat, és tegyük fel, hogy horizontjának felülete A. A fekete lyuk entrópiáját megadó Bekenstein–Hawking-képlet:
ahol k a Boltzmann-állandó, c a fénysebesség, G a Newton-féle gravitációs állandó és ħ a Planck-állandó osztva 2π-vel. A képlet lényeges része az A/4 tényező. A zárójelben álló rész csupán a szükséges fizikai állandókat tartalmazza. Egy fekete lyuk entrópiája így arányos a felületével. Gömbszimmetrikus fekete lyuknál ez a felület arányos a lyuk tömegének négyzetével:
A = m2 × 8π(G2/c2).
Beírva ezt a Bekenstein–Hawking-képletbe azt kapjuk, hogy egy fekete lyuk entrópiája tömegének négyzetével arányos:
SBH = m2 × 2π(kcG/ħ).
Így a fekete lyuk egységnyi tömegére jutó entrópia (SBH/m) a tömeggel arányos, annál nagyobb, minél nagyobb a fekete lyuk. Ezért adott tömeg – vagy Einstein E = mc2 képlete értelmében adott energia – mellett az entrópia akkor a legnagyobb, ha az egész anyag egy fekete lyukba omlik össze! Továbbmenve, két fekete lyuk entrópiája (óriási mértékben) megnövekszik, ha egymást kölcsönösen felszíva egyetlen fekete lyukká olvadnak össze! Nagy fekete lyukak, mint amilyenek a galaktikus középpontokban valószínűen találhatók, elképesztően nagy mennyiségű entrópiával rendelkeznek – messze nagyobbal, mint amilyenekkel más típusú fizikai helyzetekben találkozunk.
Csekély módosításra szorul az az állítás, hogy a legnagyobb akkor lesz az entrópia, ha az összes tömeg egyetlen fekete lyukban sűrűsödik össze. Hawking vizsgálata a fekete lyukak termodinamikájáról azt mutatja, hogy egy fekete lyukhoz egy nem zérus hőmérsékletet is hozzá kell kapcsolnunk. Ennek egyik velejárója az, hogy a maximális entrópiájú állapotban a fekete lyukon belül nincs minden energia tömeg formában, hanem egyensúly alakul ki a „sugárzás hőfürdőjével”. E sugárzás hőmérséklete ésszerű méretű fekete lyuknál valóban nagyon kicsi. Egy naptömegnyi fekete lyuknál például kb. 10–7 K, ami valamivel kisebb, mint a laboratóriumban a mai napig mért legalacsonyabb hőmérséklet, és igen jelentősen kisebb, mint a csillagközi tér 2,7 K hőmérséklete. Nagyobb fekete lyukakra a Hawking-hőmérséklet még alacsonyabb!
Vizsgálatunkban a Hawking-hőmérsékletnek csak akkor lesz jelentősége, ha vagy: (i) sokkal kisebb fekete lyukak, ún. mini fekete lyukak létezhetnek világunkban; vagy (ii) a világegyetem nem omlik össze korábban, mint a Hawking-féle párolgási idő – ami alatt a fekete lyuk teljesen elpárologna. Ami (i)-t illeti, mini fekete lyukak csak megfelelően kaotikus ősrobbanásban keletkezhetnek. Világegyetemünkben ilyenek nem lehetnek nagy számban, különben hatásaikat már megfigyelték volna; mi több, abban a szemléletben, amely szerint a dolgokat itt kifejtem, egyáltalán nincsenek. Ami (ii)-t illeti, az egy naptömegű fekete lyuk Hawking-féle párolgási ideje úgy 1054-szer nagyobb az univerzum jelenlegi koránál, nagyobb fekete lyukakra még sokkal nagyobb. Nem valószínű, hogy ezek a jelenségek lényegesen módosítanák az előbbi érvelést.
Hogy némi fogalmunk legyen a fekete lyuk entrópiájának nagyságáról, nézzük meg azt, amiről korábban úgy vélték, hogy a legnagyobb járulékot adja a világegyetem entrópiájához, nevezetesen a 2,7 K fokos feketetest-háttérsugárzást. Az asztrofizikusokat letaglózta az a hatalmas mennyiségű entrópia, amit ez a sugárzás tartalmaz, amely messze felülmúl minden közönséges entrópiaértéket, amellyel más folyamatokban (például a Napban) találkozunk. A háttérsugárzás entrópiája nagyjából 108 bariononként („természetes egységekben”, ahol a Boltzmann-állandó egységnyi). (Ez azt jelenti, hogy minden barionra 108 foton jut a háttérsugárzásból.) Ezért ha a barionok összes száma 1080, akkor az Univerzum háttérsugárzásának teljes entrópiája
1088.
Ha fekete lyukak nem lennének, akkor ez a szám adná meg a világegyetem teljes entrópiáját, mert mellette minden más, közönséges folyamat entrópiája eltörpül. A Nap egy barionjára jutó entrópia például egységnyi nagyságrendű. Másrészt viszont, a feketelyuk-mértékkel mérve, a háttérsugárzás entrópiája „hangyányi”. Minthogy a Bekenstein–Hawking-képlet azt mondja, hogy az egy naptömegű fekete lyukban az entrópia bariononként természetes egységekben kb. 1020, ezért ha az egész világegyetem naptömegű fekete lyukakból állna, akkor a teljes entrópia az előbb megadottnál sokkal nagyobb, nevezetesen
10100
lenne. A világegyetem természetesen nem ilyen, ám ez a szám már mond valamit arról, mennyire „kicsinek” kell tekintenünk a háttérsugárzás entrópiáját, amikor a gravitáció könyörtelen hatásait is figyelembe vesszük.
Próbáljunk meg egy kicsivel realisztikusabbak lenni! Ne népesítsük be galaxisainkat teljesen fekete lyukakkal, vegyük úgy, hogy főként közönséges csillagokat – nagyságrendben 1011-t – tartalmaznak, és mindegyik magjában van egy egymillió (azaz 106) naptömegű fekete lyuk (ami saját Tejútrendszerünknél ésszerűnek látszik). A számítások azt mutatják, hogy az egy barionra jutó entrópia most valamivel még az előbbi hatalmas számnál is nagyobb, 1021, tehát a teljes entrópia természetes egységekben
10101.
Előre megjósolhatjuk, hogy nagyon hosszú idő múlva a galaxisok tömegének nagy hányada a középpontban ülő fekete lyukba kerül. Amikor ez bekövetkezik, az egy barionra jutó entrópia 1031 lesz, a teljes entrópia pedig
10111.
Azonban zárt világegyetemet vizsgálunk, amelynek végül össze kell esnie; ezért nem ésszerűtlen, ha a Bekenstein–Hawking-képletet használva úgy becsüljük meg a végső roppanás entrópiáját, mintha az egész világegyetem egy fekete lyukat képezne. Így 1043 nagyságú entrópiát kapunk bariononként, és az abszolút elképesztő
10123
értéket a Nagy Roppanás teljes entrópiájára.
E szám alapján megbecsülhetjük a Teremtő rendelkezésére álló V teljes fázistér-térfogatot, mert ez az entrópia a (messze) legnagyobb tartomány térfogatának logaritmusával egyenlő. Minthogy 10123 a térfogat logaritmusa, a térfogat a 10123-ik hatvánnyal kell egyenlő legyen, azaz
természetes egységekben! (A figyelmes Olvasó észreveheti, hogy az
számot kellett volna írnom, ám az ilyen nagyságú számoknál az e és a 10 lényegében felcserélhető!) Milyen nagy volt az az eredeti W fázistér-térfogat, amelyet a Teremtőnek meg kellett céloznia, hogy olyan világegyetemet alkosson, amely összhangban van a termodinamika második főtételével, és azzal, amelyet ma megfigyelünk? Nem sokat számít, hogy a
értéket vesszük, az egyiket a galaktikus fekete lyukak, a másikat a háttérsugárzás adja, vagy egy sokkal kisebbet (és ténylegesen sokkal alkalmasabbat), amely az igazi szám volt a Nagy Robbanásnál. Akár így, akár úgy, V és W hányadosa közelítőleg
Ez most megmondja nekünk, mennyire pontosan kellett céloznia a Teremtőnek: ez a pontosság
Ez valami fantasztikus szám. A közönséges tízes jelölésben még leírni sem tudnánk: egy „1”-est 10123 „0” követne! Még ha a teljes világegyetem minden egyes protonjára és neutronjára írnánk egy „0”-t – és ráadásul még az összes többi részecskét is beállítanánk e sorba –, messze nem tudnánk még akkor sem leírni e számot. A világegyetem útjára indításához szükséges pontosság láthatóan semmivel sem kisebb, mint mindaz a rendkívüli pontosság, amelyhez már hozzászoktunk a (Newton-, Maxwell-, Einstein-) szuper dinamikai egyenletekben, amelyek a dolgok viselkedését kormányozzák pillanatról pillanatra.
De miért volt a Nagy Robbanás olyan pontosan szervezett, mikor a Nagy Roppanás (vagy a szingularitások a fekete lyukakban) várhatóan teljesen kaotikus? E kérdés, úgy tetszik, a téridőgörbület WEYL részének a téridő-szingularitásokban mutatott viselkedését érinti. Azt találjuk, hogy a kezdeti téridő-szingularitásoknál fennáll a
WEYL = 0
(vagy ehhez nagyon hasonló más) megszorítás – de a végső szingularitásoknál nem –, és ez, úgy látszik, a Teremtő választását a fázistér nagyon kis tartományára korlátozza. A feltevést, mely szerint a megszorítás érvényes minden kezdeti téridő-szingularitásra (de a végsőkre nem), Weyl-féle görbületi hipotézisnek nevezem. Így tehát azt kellene megértenünk, miért kell ilyen időaszimmetrikus hipotézist alkalmaznunk, ha ki akarjuk deríteni, honnan ered a második főtétel.153
Honnan szerezhetünk további információt a második főtétel eredetéről? Úgy látszik, zsákutcába jutottunk. Meg kell értenünk, miért olyan a téridő-szingularitások szerkezete, mint amilyennek mutatkozik; ám a téridő-szingularitások olyan tartományok, ahol fizikai megértésünk eléri korlátait. A szingularitások létezéséből keletkező zsákutcát olykor egy másikhoz hasonlítják: ezzel a fizikusok a század elején találkoztak az atomok stabilitásával kapcsolatban (lásd 6. fejezet). A jól megalapozott klasszikus elmélet mindkét esetben a „végtelen” választ adta, ezzel magát a feladatra alkalmatlannak nyilvánította. Az atomok szinguláris elektromágneses összeomlását a kvantumelmélet oldotta fel; hasonlóképpen a kvantumelméletnek kellene egy véges elméletet állítania a „végtelen” klasszikus téridő-szingularitások helyébe a csillagok gravitációs összeomlásában. Ám ez nem lehet a közönséges kvantumelmélet. Magának a tér és idő szerkezetének kvantumelmélete kell legyen. Ha létezne ilyen, akkor „kvantumgravitációnak” hívnák. Hiánya nem a fizikusok erőfeszítésein, ügyességén, leleményességén múlik. Sok elsőrangú tudós elme szentelte magát egy ilyen elmélet kidolgozásának, ám siker nélkül. Ez az a zsákutca, amelybe végül bevittek szándékaink, hogy megértsük az idő irányítottságát, folyását.
Az Olvasó joggal kérdheti, mire jutottunk az utazásunk során. Kutatásunkban, hogy megértsük, miért halad az idő csak az egyik irányban, a másikban nem, el kellett utaznunk az idők végéig, ahol a maga a térfogalom is szétmállik. Mit tanultunk mindebből? Azt, hogy elméleteink még nem megfelelőek a válasz megadására, de mennyiben segít ez bennünket az értelem megértésére irányuló igyekezetünkben? A megfelelő elmélet hiánya ellenére azt hiszem, hogy utazásunk során valóban fontos leckéket tanulhattunk meg. Most vissza kell fordulnunk hazafelé. Visszautunk még spekulatívabb lesz, ám véleményem szerint más ésszerű választásunk nincs!
...A feltevést, mely szerint a megszorítás érvényes minden kezdeti téridő-szingularitásra (de a végsőkre nem), Weyl-féle görbületi hipotézisnek nevezem. Így tehát azt kellene megértenünk, miért kell ilyen időaszimmetrikus hipotézist alkalmaznunk, ha ki akarjuk deríteni, honnan ered a második főtétel.153...
A "Weyl-féle görbületi hipotézis" és a termodinamika második főtétele eredetének kérdése, mint az 'ősokok' kérdése. Hogyan is válaszolt Lali az entrópiára vonatkozó kérdésemre?:nehéz...
153 Van egy jelenleg népszerű szemléletmód, az ún. „inflatorikus forgatókönyv”, amely arra irányul, hogy megmagyarázza, miért olyan egyenletes a világegyetem nagy skálán. Eszerint az univerzum nagyon korai szakaszában hatalmas táguláson ment keresztül – sokkal nagyobb méretűn, mint a standard modell „közönséges” tágulása. Az elképzelés az, hogy ez a tágulás minden szabálytalanságot kisimított. Ám valamiféle még nagyobb kezdeti megszorítás nélkül, mint amilyet a Weyl-féle görbületi hipotézis már szolgáltat, az infláció nem működik. Nem vezet be semmilyen idő-aszimmetrikus elemet, amely magyarázni tudná a kezdeti és végső szingularitások különbözőségét. (Mi több, nem megalapozott fizikai elméletekre – a GUT elméletekre – támaszkodik, amelyek helyzete, az 5. fejezetben használt minősítéssel, nem jobb, mint KÍSÉRLETI. Az „infláció” egy kritikai ismertetését illetően, összefüggésben az e fejezetbeli elképzelésekkel, lásd Penrose 1989b.)
Ocham borotvája. Penrose láthatólag nem szíveli az olyan magyarázatokat, amelyek egy eleddig ismeretlen, vagy megválaszolatlan jelenséget nem a meglévő tudásunkra alapozva próbálnak leírni, hanem a levezetésükhöz még további ellenőrizhetetlen, nem bizonyított, vagy hibás, ingatag fizikai alapokra épített feltevéseket vezetnek be.
Mit tanultunk mindebből? Azt, hogy elméleteink még nem megfelelőek a válasz megadására, de mennyiben segít ez bennünket az értelem megértésére irányuló igyekezetünkben? -
kérdi, de ez egyáltalán nem a reménytelenség kérdése.
8. Kutatjuk a kvantumgravitációt
Miért a kvantumgravitáció?
Mi újat lehet megtanulnunk az agyra és értelemre vonatkozóan abból, amivel az előző fejezetben találkoztunk? Bár felvillantak azok a mindent átfogó fizikai elvek, amelyek „időfolyás” érzékelésünk irányítottságának alapjául szolgálnak, mindeddig nem látszik, hogy bepillantást nyertünk volna a kérdésbe, miért érzékeljük az idő folyását, vagy miért érzékelünk egyáltalán. Véleményem szerint sokkal radikálisabb elképzelésekre van szükség. Előadásom eddig nem volt különösebben radikális, bár olykor a szokásostól eltérő hangsúlyokat használtam. Megismerkedtünk a termodinamika második főtételével, és igyekeztem meggyőzni az Olvasót, hogy e törvényt – amilyen speciális formában a Természet kiválasztotta, hogy átnyújtsa nekünk – a világegyetem Nagy Robbanáseredetére fennálló nagyon erős geometriai megszorításig lehet visszavezetni: ez a Weyl-féle görbületi hipotézis. Egyes kozmológusok esetleg némiképp eltérően szeretik jellemezni e kezdeti megszorítást, ám a kezdeti szingularitásra mindenképpen ki kell ilyet róni. A következtetések, amelyeket e hipotézisből felvázolni készülök, sokkal kevésbé lesznek hagyományosak, mint maga a hipotézis. Azt állítom, hogy a kvantumelmélet kereteit kell megváltoztatnunk!
E változtatás akkor jut szerephez, amikor megfelelően egyesítjük a kvantummechanikát és az általános relativitáselméletet, azaz megalkotjuk a kvantumgravitáció keresett elméletét. A legtöbb fizikus nem hiszi, hogy a kvantumelméletet meg kellene változtatni, és így egyesíteni az általános relativitáselmélettel. Mi több, úgy érvelnének, hogy az agyunk működésében lényeges skálán bármiféle kvantumgravitáció fizikai hatásai teljesen lényegtelenek kell legyenek! Azt mondanák (nagyon ésszerűen), hogy noha az ilyen fizikai jelenségek valóban fontosak lehetnek a Planck-hosszúság154 néven ismert elképesztően kicsiny távolságskálán – amely 10–35 m, néhány 100 000 000 000 000 000 000-szer kisebb a legparányibb szubatomi részecske méreténél –, közvetlen jelentőségük nem lehet semmiféle jelenségnél a sokkal-sokkal nagyobb, mondjuk 10–12 m-ig terjedő „közönséges” skálákon, ahol az agyműködésben fontos kémiai vagy elektromos folyamatok uralkodnak. Valóban, még a klasszikus (azaz nem kvantumos) gravitációnak sincs majdnem semmi befolyása ezekre az elektromos és kémiai folyamatokra. Ha a klasszikus gravitációnak nincs hatása, akkor hogy a csudában lehetne a klasszikus elmélet bármilyen apró „kvantumos korrekciójának”? Továbbmenve: minthogy soha nem figyeltek meg eltéréseket a kvantumelmélettől, még inkább ésszerűtlennek látszik azt képzelni, hogy bármilyen feltételezett parányi eltérés a szabványos kvantumelmélettől szerepet játszhat a szellemi jelenségekben!
Érvelésem egészen más lesz. Nem azzal törődöm, milyen hatásai lehetnek a kvantummechanikának a téridő szerkezetéről alkotott elméletünkre (Einstein általános relativitáselméletére), hanem a fordított kérdéssel: milyen hatásai lehetnek Einstein téridőelméletének a kvantummechanika szerkezetére. Hangsúlyozom, hogy egy nem hagyományos nézőpontot vázolok fel. Nem hagyományos az, hogy az általános relativitásnak egyáltalán bármiféle hatása legyen a kvantummechanika szerkezetére! A hagyományokat tisztelő fizikusok nagyon vonakodnak azt gondolni, hogy a kvantummechanika megszokott szerkezetébe bármilyen módon bele kell nyúlni. Noha igaz, hogy a kvantumelmélet szabályainak közvetlen alkalmazása Einstein elméletére láthatóan leküzdhetetlen nehézségekbe ütközik, az e területen dolgozó kutatók hajlamosak ebből arra következtetni, hogy Einstein elméletét kell módosítani, nem a kvantumelméletet.155 Az én nézőpontom majdnem ellentétes ezzel. Úgy vélem, hogy a problémák magán a kvantumelméleten belül alapvetőek. Emlékezzünk az összhang hiányára a kvantummechanika U és R eljárásai között (U a tökéletesen determinisztikus Schrödinger-egyenletnek engedelmeskedik – unitér fejlődésnek hívják –, R pedig a valószínűségi állapotvektor-redukció, amelyet akkor kell alkalmaznunk, amikor „megfigyelés” történt.) Nézetem szerint ez olyan összeférhetetlenség, amelyet nem lehet megfelelően feloldani csupán a kvantummechanika alkalmas „értelmezésével” (noha az általános nézet szerint valahogyan meg kell tudni ezt tenni), hanem csak radikálisan új elmélettel, amely szerint a két eljárás, U és R különböző (és kitűnő) közelítései egyetlen átfogóbb és egzakt eljárásnak. Ezért úgy gondolom, hogy még a kvantummechanika csodálatosan pontos elméletét is meg kell változtatnunk, és e változtatás természetére Einstein általános relativitáselméletéből jön komoly útmutatás. Még tovább megyek, és azt mondom, hogy ténylegesen a kvantumgravitáció keresett elmélete az, amelynek egyik alapvető összetevőjeként tartalmaznia kell e feltételezett összetett U/R eljárást.
A hagyományos szemléletben viszont a kvantumgravitáció minden közvetlen velejárója elvontabb természetű volna. Említettem a várakozást, hogy a téridő szerkezete alapvetően megváltozik a Planck-hosszúság képtelenül parányi skáláján. Fennáll az a (véleményem szerint igazolt) hiedelem is, hogy végső soron a kvantumgravitációnak kellene alapjaiban meghatároznia az „elemi részecskék” jelenleg megfigyelt seregletének természetét. Ma például nincs jó elmélet annak magyarázatára, miért éppen akkorák a részecskék tömegei, amekkorák – márpedig a „tömeg” fogalom szoros kapcsolatban áll a gravitáció fogalmával. (A tömeg a gravitáció kizárólagos „forrása”.) Értelmes várakozás az is, hogy (a svéd fizikus, Oskar Klein által 1955 körül felvetett gondolat szerint) a kvantumgravitáció helyes elmélete kell eltávolítsa a hagyományos kvantummező-elméletet sújtó végteleneket (lásd 6. fejezet). A fizika egy egység, és az igazi kvantumgravitáció elmélete, amikor végül a birtokunkban lesz, biztosan jelentős részét képezi majd a Természet egyetemes törvényeiről alkotott részletes tudásunknak.
Ám ettől még messze vagyunk. Mi több, minden feltételezett kvantumgravitáció-elmélet bizonyára nagyon távol esik az agy viselkedését szabályozó jelenségektől. Az agyműködéstől különösen távolinak látszik a kvantumgravitációnak az az (általánosan elfogadott) szerepe, amely a zsákutcából való kivezetéshez szükséges, amelybe az előző fejezet végén kerültünk: a téridő-szingularitások problémája. Ezek Einstein klasszikus elméletének szingularitásai, amelyek a Nagy Robbanásnál és a fekete lyukakban lépnek fel – és a Nagy Roppanásnál is, ha világegyetemünk végül úgy dönt, hogy önmagába omlik össze. Igen, ez a szerep nagyon távolinak tűnhet. Érveket hozok azonban fel amellett, hogy létezik a logikai kapcsolatnak egy tünékeny, de fontos szála. Próbáljuk megnézni, mi is ez a kapcsolat.
155 Ilyen népszerű módosítások a következőek: (i) a RICCI = ENERGIA Einstein-egyenletek megváltoztatása („magasabb rendű Lagrange-függvények” segítségével); (ii) a táridő dimenziószámának megváltoztatása négyről egy nagyobb számra (mint az ún. „Kaluza–Klein-típusú elméletekben”); (iii) a „szuperszimmetria” bevezetése (egy, a bozonok és fermionok kvantumos viselkedéséből kölcsönvett elképzelés beépítve egy átfogó rendszerbe és alkalmazva, nem egészen logikusan, a téridő-koordinátákra); (iv) a húrelmélet [egy jelenleg népszerű, radikális elgondolás, amelyben a „világvonalakat” a „húrtörténetek” helyettesítik – rendszerint összekombinálva az (ii) és (iii) elképzelésekkel]. Mindezek a javaslatok népszerűségük és erőteljes előadásuk ellenére határozottan a KÍSÉRLETI kategóriába tartoznak az 5. fejezet osztályozása szerint.
Alig várom már ezt a tünékeny, ám fontos szálat, hogy megjelenjék.
Mi van a Weyl-féle görbületi hipotézis mögött?
Mint azt megjegyeztem, még a hagyományos nézőpont is azt mondja, hogy a kvantumgravitáció jön majd a klasszikus általános relativitáselmélet segítségére, hogy megoldja a téridő-szingularitások rejtélyét. Így a kvantumgravitáció kell ellásson bennünket egy összefüggő fizikai képpel a klasszikus elmélet értelmetlen „végtelen” válaszai helyett. Ezzel a nézettel biztosan egyetértek: ez valóban világos hely, ahol a kvantumgravitációnak le kell tennie névjegyét. Ám az elméletiek, úgy látszik, nem sokat törődnek azzal a meglepő ténnyel, hogy a kvantumgravitáció névjegye otrombán időaszimmetrikus! A Nagy Robbanásnál – a múltbéli szingularitásnál – a kvantumgravitációnak egy a
WEYL = 0
feltételhez hasonlót kell biztosítania abban a pillanatban, amikor értelmessé válik a téridő-geometria klasszikus fogalmainak használata. A fekete lyukak belsejében lévő szingularitásoknál és a (lehetséges) Nagy Roppanásnál – a jövőbéli szingularitásoknál – viszont nincs ilyen megszorítás, és azt várjuk, hogy a Weyl-tenzor végtelenné válik:
WEYL → ∞,
ahogy a szingularitáshoz közeledünk. Véleményem szerint világos a jelzés, hogy az elméletnek, amelyet keresünk, az időben aszimmetrikusnak kell lennie:
a keresett kvantumgravitáció időaszimmetrikus elmélet kell legyen.
Figyelmeztetem itt az Olvasót, hogy e következtetés, annak ellenére, hogy a dolgok bemutatásának általam választott módjából láthatóan szükségszerűen adódik, nem elfogadott bölcsesség! A terület legtöbb kutatója nagyon nem akarja e szemléletet elfogadni. Az ok, úgy látszik, az, hogy a hagyományos és jól megértett kvantálási eljárásokban (ahogy most állnak) nincs világos lehetőség időaszimmetrikus156 kvantált elmélet létrehozására, amikor a klasszikus elmélet, amelyre ezeket az eljárásokat alkalmazzák (a szabványos általános relativitás vagy valamelyik népszerű módosítása), maga időszimmetrikus. Ezek szerint (ha egyáltalán foglalkoznak ilyen kérdésekkel – ami nem gyakori!) az ilyen gravitációkvantálóknak máshol kell keresniük a Nagy Robbanás alacsony entrópiájának „magyarázatát”.
Talán sok fizikus érvelne úgy, hogy egy hipotézis, mint a Weyl-görbület kezdeti eltűnését kimondó, lévén „határfeltétel”-választás és nem fizikai törvény, nem olyan valami, amit a fizikának meg kell magyaráznia. Ők úgy érvelnek, hogy kaptunk egy „isteni cselekedetet”, és nem kell törekednünk megérteni, miért az egyik határfeltételt kaptuk, és nem egy másikat. Ám mint láttuk, a kényszer, amit e hipotézis a „Teremtő tűjére” kirótt, nem kevésbé különleges és pontos, mint az az egész figyelemre méltó és finoman szervezett koreográfia, amelyet a Newton, Maxwell, Einstein, Schrödinger, Dirac és mások egyenletein keresztül megértett dinamikai törvények alkotnak. Noha a termodinamika második főtétele homályosnak és statisztikus jellegűnek látszódhat, egy nagyon nagy pontosságú geometriai kényszerből származik. Számomra ésszerűtlennek látszik, hogy ne akarjuk tudományosan megérteni a kényszereket, amelyek a „kezdeti feltételben”, a Nagy Robbanásban működtek, amikor a tudományos megközelítés oly értékesnek bizonyult a dinamikai egyenletek megértésében. Én úgy gondolkodom, hogy az előbbi éppen olyan része a tudománynak, mint az utóbbi, noha egyelőre nem értjük jól.
A tudomány története megmutatta, mennyire értékes ez az elképzelés, amely szerint a fizika dinamikai egyenleteit (Newton-törvényeket, Maxwell-egyenleteket stb.) elválasztják az ún. határfeltételektől – amelyeket azért kell kiszabni, hogy az egyenletek fizikailag megfelelő megoldását (megoldásait) ki lehessen választani a nem megfelelőek mocsarából. Történetileg a dinamikai egyenletek lettek egyszerű alakúak. A részecskék mozgásai egyszerű törvényeket elégítenek ki, de a részecskék tényleges elrendezései, amelyekkel a világegyetemben találkozunk, már gyakran nem ilyenek. Olykor ezek az elrendezések első ránézésre egyszerűeknek tűnnek – mint a bolygómozgás Kepler által kiderített elliptikus pályái –, de ez az egyszerűség olyankor a dinamikai törvények következménye. A mélyebb megértést mindig a dinamikai törvényekből szereztük, és az ilyen egyszerű elrendezések általában csupán közelítései sokkal bonyolultabbaknak, mint például a ténylegesen megfigyelt, perturbált (nem egészen elliptikus) bolygómozgásoknak, amelyeket Newton dinamikai egyenletei magyaráznak. A határfeltételek a szóban forgó rendszer „indításához” szolgálnak, utána a dinamikai egyenletek veszik át az irányítást. A természettudományok egyik legfontosabb felismerése az, hogy a dinamikai viselkedést elválaszthatjuk attól a kérdéstől, hogy a világegyetem tényleges tartalma hogy van elrendezve.
Azt mondtam, hogy ez a szétválasztás dinamikai egyenletekre és határfeltételekre történetileg létfontosságú volt. Hogy az ilyen szétválasztás egyáltalán lehetséges, az az egyenletek speciális típusának (differenciálegyenleteknek) egyik tulajdonsága, a fizikában mindig ilyenek fordulnak elő. Nem hiszem azonban, hogy e felosztás meg fog maradni. Véleményem szerint, amikor majd végleg megértjük a törvényeket vagy elveket, amelyek világegyetemünk viselkedését ténylegesen szabályozzák – és nem csupán a csodálatos közelítéseket, amelyeket kezdünk megérteni, és amelyek a mai SZUPER elméleteinket képezik –, akkor azt fogjuk látni, hogy e megkülönböztetés dinamikai egyenletek és határfeltételek között eltűnik. Lesz helyette valamilyen csodálatosan következetes, átfogó rendszer. Természetesen, mikor ezt mondom, saját, személyes véleményemet fejezem ki. Lehet, hogy sokan nem értenek velem egyet. De agyamban homályosan ez a nézőpont rajzolódik ki, amikor megpróbálom kideríteni a kvantumgravitáció ismeretlen elméletének velejáróit. (E nézőpont befolyásolni fogja az utolsó fejezet egyes spekulatívabb megfontolásait is.)
Hogyan tárhatjuk fel egy ismeretlen elmélet következményeit? Lehet, hogy a dolgok távolról sem olyan reménytelenek, mint amilyennek látszanak. A kulcs a következetesség! Az Olvasót először arra kérem, fogadja el, hogy feltételezett elméletünk – amelyre a KKG („korrekt kvantumgravitáció”!) jelölést fogom használni – magyarázatát fogja adni a Weyl-féle görbületi hipotézisnek (WGH). Ez azt jelenti, hogy a kezdeti szingularitásokra fennáll a megszorítás, hogy a szingularitás közvetlen jövőjében WEYL = 0. E megszorítás összhangban kell legyen a KKG törvényeivel, ezért fenn kell álljon tetszőleges „kezdeti szingularitásra”, nem csak a „Nagy Robbanásnak” nevezett speciálisra. Nem azt mondom, hogy világegyetemünkben kell lennie más kezdeti szingularitásnak, mint a Nagy Robbanásnak, az a lényeg, hogy ha volna, akkor erre is fennállna a WGH megszorítás. A kezdeti szingularitás olyan, hogy belőle, elvileg, részecskék jöhetnének ki. Éppen ellentétesen viselkednek a fekete lyukak szingularitásai lévén azok a végső szingularitások, amelyekbe a részecskék beeshetnek.
Egy lehetséges, a Nagy Robbanástól eltérő típusú, kezdeti szingularitás a fehér lyukban lévő – ez, mint a 7. fejezetből visszaidézhetjük, a fekete lyuk időmegfordítottja (nézzük meg ismét a 7.14. ábrát). Láttuk azonban, hogy a fekete lyukakon belül lévő szingularitások a WEYL → ∞ feltételt elégítik ki, így ennek egy fehér lyukra is fenn kell állnia. De ez most egy kezdeti szingularitás, amelyre a WGH megköveteli, hogy WEYL = 0 legyen. Ezért a WGH kizárja a fehér lyukak jelenlétét világegyetemünkben! (Szerencsére ez nemcsak termodinamikai szempontokból kívánatos – minthogy a fehér lyukak nagyon nem engedelmeskednek a második főtételnek –, hanem a megfigyelésekkel is összhangban van! Különböző asztrofizikusok időnként fehér lyukak létezését követelték meg, hogy bizonyos jelenségeket megmagyarázzanak, ám ez mindig több problémát vet fel, mint amennyit megold.) Megjegyzem, hogy magát a Nagy Robbanást nem nevezem „fehér lyuknak”. Egy fehér lyukban lokalizált kezdeti szingularitás bújik meg, amely nem képes teljesíteni a WEYL = 0 feltételt; ám a mindent átfogó Nagy Robbanásban lehet WEYL = 0, létezését a WGH megengedi, feltéve, hogy e megszorítás fennáll.
Van egy más típusú lehetséges „kezdeti szingularitás”: nevezetesen egy olyan fekete lyuk felrobbanásának eseménye, amely (mondjuk) 1064 évi Hawking-párolgás után végül eltűnt (lásd a 7. és a 8. fejezetet)! Sokat töprengtek e (nagyon elfogadható) feltételezett jelenség pontos természetén. Úgy gondolom, hogy ez valószínűleg nem kerül összeütközésbe a WGH-val. Egy ilyen (lokalizált) robbanás pillanatszerű és szimmetrikus lehetne, nem látok ellentmondást a WEYL = 0 hipotézissel. (Mindenesetre, feltételezve, hogy mini fekete lyukak nincsenek (vö. 7. fejezet), valószínű, hogy az első ilyen robbanás csak azután fog bekövetkezni, hogy a világegyetem már 1054-szer annyi ideig létezett, mint mai T életkora! Hogy érzékeljük, milyen hosszú idő 1054 T, képzeljük azt, hogy T-t összezsugorítjuk a legrövidebb mérhető időre – az instabil részecskék legkisebb bomlási idejére –: ekkor jelenlegi világegyetemünk tényleges kora ezen a skálán milliószor milliónál is nagyobb szorzótényezővel maradna el a 1054-től!
Egyesek az általam javasolttól eltérő vonalat követnek. Úgy érvelnek,157 hogy a KKG-nek nem kellene időaszimmetrikusnak lennie, ám meg kellene engednie két típusú szingularitásszerkezetet; az egyik megkövetelné a WEYL = 0 feltételt, a másik megengedné, hogy WEYL → ∞. Világegyetemünkben történetesen az első típusú szingularitás van, és időirány-érzékelésünk (a következetes második főtétel miatt) olyan, hogy e szingularitást odahelyezzük, amit „múltnak” hívunk, és nem oda, amit „jövőnek”. Ám én úgy látom, hogy ez az érvelés, ahogy van, nem megfelelő. Nem magyarázza meg, miért nincs más, WEYL → ∞ típusú kezdeti szingularitás (vagy egy másik WEYL = 0 típusú). Mit mond e szemlélet, miért nincs a világegyetem teleszórva fehér lyukakkal? Minthogy feltételezhetően tele van szórva feketékkel, meg kell magyarázni, miért nincsenek fehérek.158
Egy másik érvelés, amely olykor megjelenik ebben az összefüggésben, az úgynevezett emberközpontú elv (vö. Barrow és Tipler 1986). Eszerint azt a speciális világegyetemet, amelyet ténylegesen benépesítünk, az összes lehetséges világegyetem közül kiválasztja az a tény, hogy megfigyeléséhez nekünk (vagy legalább valamilyen érző teremtményeknek) jelen kell lennünk! (Ezt az elvet a 10. fejezetben ismét tárgyalni fogom.) Ebből az érvelésből azt az állítást vezetik le, hogy intelligens lények csak nagyon speciális típusú nagy robbanásban született világegyetemben élhetnek – ezért az elv következménye lehet valami WGH-hoz hasonló feltétel. Ám az érvelés sehol nem képes a szükséges, a 7. fejezetben megkapott
szám, a Nagy Robbanás „különlegessége” közelébe jutni. Nagyon durva számítás azt mutatja, hogy lakóival együtt a teljes naprendszer sokkal „olcsóbban” létrejöhetett volna a részecskék véletlenszerű ütközéseiben, nevezetesen „csak” egy rész a 1010-nál sokkal kisebben „valószínűtlenséggel” (fázistér-térfogatokban mérve). Ez minden, amit az emberközpontú elv tenni tud értünk, és még rettenetesen messze vagyunk a kívánt számtól. Mi több, az előbb említett nézőponthoz hasonlóan az emberközpontú elv sem kínál magyarázatot a fehér lyukak hiányára.
156 Noha a kvantálási eljárások nem mindig őrzik meg a klasszikus elmélet szimmetriáit (vö. Treiman 1985, Ashtekar és mások 1989), itt egyszerre négy szimmetria sértésére van szükség, melyek jelölése általában T, PT, CT és CPT. Ez (különösen a CPT-sértés) meghaladni látszik a hagyományos kvantálási módszerek erejét.
157 Amennyire fel tudom fogni, egy ilyen jellegű szemléletmód hallgatólagosan ott van Hawking javaslataiban e dolgok kvantumgravitációs magyarázatára (Hawking 1987, 1988). Hartle és Hawking (1984) egy javaslata a kezdeti állapot kvantumgravitációs eredetére esetleg elméleti jelentőséget adhat egy WEYL = 0 típusú kezdeti feltételnek, ám (véleményem szerint) lényeges időaszimmetrikus bemenet mindeddig hiányzik ezekből az elképzelésekből.
158 Lehet (helyesen) úgy érvelni, hogy a megfigyelések semmiképpen nem elegendőek állításom alátámasztására, miszerint a világegyetemben fekete lyukak vannak, de fehérek nincsenek. Am érvelésem alapvetően elméleti. A fekete lyukak összhangban vannak a termodinamika második főtételével, a fehérek viszont nincsenek! (Természetesen egyszerűen posztulálhatnánk a második főtételt és a fehér lyukak hiányát; ám ennél mélyebben próbáljuk keresni a második főtétel eredetét.)
Talán sok fizikus érvelne úgy, hogy egy hipotézis, mint a Weyl-görbület kezdeti eltűnését kimondó, lévén „határfeltétel”-választás és nem fizikai törvény, nem olyan valami, amit a fizikának meg kell magyaráznia. Ők úgy érvelnek, hogy kaptunk egy „isteni cselekedetet”, és nem kell törekednünk megérteni, miért az egyik határfeltételt kaptuk, és nem egy másikat. Ám mint láttuk, a kényszer, amit e hipotézis a „Teremtő tűjére” kirótt, nem kevésbé különleges és pontos, mint az az egész figyelemre méltó és finoman szervezett koreográfia, amelyet a Newton, Maxwell, Einstein, Schrödinger, Dirac és mások egyenletein keresztül megértett dinamikai törvények alkotnak. Noha a termodinamika második főtétele homályosnak és statisztikus jellegűnek látszódhat, egy nagyon nagy pontosságú geometriai kényszerből származik. Számomra ésszerűtlennek látszik, hogy ne akarjuk tudományosan megérteni a kényszereket, amelyek a „kezdeti feltételben”, a Nagy Robbanásban működtek, amikor a tudományos megközelítés oly értékesnek bizonyult a dinamikai egyenletek megértésében. Én úgy gondolkodom, hogy az előbbi éppen olyan része a tudománynak, mint az utóbbi, noha egyelőre nem értjük jól.
...
Én úgy gondolkodom, hogy az előbbi éppen olyan része a tudománynak, mint az utóbbi, noha egyelőre nem értjük jól.- A megértésnek ez a legyőzhetetlen vágya hajtja még 92 éves korában is.
Időaszimmetria az állapotvektor-redukcióban
Úgy látszik, valóban itt maradtunk azzal a következtetéssel, hogy a KKG időaszimmetrikus elmélet kell legyen, amelynek egyik következménye a WGH (vagy valami nagyon hasonló). Hogyan lehetséges idősszimmetrikus elméletet kapnunk két időszimmetrikus alkotórészből: a kvantumelméletből és az általános relativitáselméletből? Kiderül, hogy erre van egy sor elképzelhető technikai lehetőség, amelyek egyike sincs még igazán feltárva (vö. Ashtekar és mások 1989). Am én ettől eltérő irányban óhajtok vizsgálódni. Jeleztem, hogy a kvantumelmélet „időszimmetrikus”, de ez valójában csak az elmélet U részére (Schrödinger-egyenlet stb.) vonatkozik. A 7. fejezet elején a fizikai törvények időszimmetriájáról folytatott vizsgálataimban megfontoltan távol tartottam magam az R résztől (a hullámfüggvény-redukciótól). Uralkodónak látszik az a nézet, hogy R szintén időszimmetrikus kell legyen. Lehet azért, mert sokan viszolyognak attól, hogy R-et tényleges, U-tól független „eljárásnak” tekintsék; ekkor U időszimmetriája maga után kellene vonja R időszimmetriáját is. Szeretnék érvelni, hogy ez nincs így: R időaszimmetrikus – legalábbis akkor, ha egyszerűen azt a fizikusok által elfogadott eljárást jelenti, amellyel valószínűségeket számítanak a kvantummechanikában.
Hadd emlékeztessem először az Olvasót a kvantummechanikában alkalmazott eljárásra, amelyet állapotvektor-redukciónak (R) neveznek (6.23. ábra). A 8.1. ábrán felvázoltam a |ψ〉 állapotvektor különös fejlődését a kvantummechanikában. E fejlődés legnagyobb részében az U unitér fejlődést követi (Schrödinger-egyenlet), de bizonyos időpontokban, amikor egy „megfigyelés” (vagy „mérés”) megtörténtét feltételezzük, az R eljárást fogadjuk el, ekkor a |ψ〉 állapotvektor egy másik állapotvektorba, mondjuk ∣χ〉-be ugrik át, ahol ∣χ〉 egyike a két vagy több, ∣χ〉, ∣φ〉, ∣θ〉, … ortogonális alternatívának, amelyeket a végrehajtott speciális O megfigyelés természete határoz meg. A |ψ〉-ból ∣χ〉-be való átugrás p valószínűségét az a mennyiség adja meg, amennyivel |ψ〉 négyzetes hossza, |ψ〉2 csökken, amikor (a Hilbert-tér) ∣χ〉 irányára vetítjük. (Ez matematikailag ugyanaz a mennyiség, mint amennyivel ∣χ〉2 csökkenne, ha ∣χ〉-t vetítenénk |ψ〉 irányába.) Ez az eljárás időaszimmetrikus, mert az O megfigyelés után közvetlenül az állapotvektor egyike az O által meghatározott ∣χ〉, ∣φ〉, ∣θ〉, … alternatív lehetőségeknek, míg közvetlenül O előtt az állapotvektor |ψ〉, amely nem feltétlenül egyike az adott alternatíváknak. Am ez az aszimmetria csak látszólagos, és az állapotvektor fejlődésének egy különböző nézőpontját véve orvosolható. Tekintsünk egy időfordított kvantummechanikai fejlődést. E különcködő leírást a 8.2. ábra mutatja. Vegyük most az állapotot ∣χ〉-nek közvetlenül O előtt, és nem utána, és alkalmazzuk az unitér fejlődést időben visszafelé, a megelőző O’ megfigyelés időpontjáig. Tegyük fel, hogy e visszafelé fejlődő állapot ∣χ〉-vé válik (közvetlenül az O’ megfigyelés jövőjéig). A 8.1. ábra rendes, előre fejlődő leírásában valamilyen más, |ψ〉 állapotunk volt O’ közvetlen jövőjében (ez volt az O’ megfigyelés eredménye, utána |ψ’〉 a rendes leírásban fejlődött előre az O-nál meglévő |ψ〉-be). Na már most, fordított leírásunkban a |ψ’〉 állapotvektornak is megvan a szerepe: ez adja meg a rendszer állapotát közvetlenül O’ múltjában. A |ψ’〉 állapotvektor írja le az O’-ben ténylegesen megfigyelt állapotot, ezért a hátrafelé fejlesztő nézőpontunkban most azt gondoljuk, hogy |ψ’〉 az az állapot, amely a megfordított idő értelemben az O’ megfigyelés „eredménye”. Az O’ megfigyelés eredményét az O-éhoz viszonyító p’ kvantumos valószínűséget most az adja meg, milyen mértékben csökken ∣χ’〉2 ∣χ’〉-nek |ψ’〉 irányára való vetítése során (ez egyenlő azzal, amilyen mértékben |ψ’〉2 csökken |ψ’〉-nek ∣χ’〉 irányára való vetítésekor). Az U művelet alaptulajdonsága, hogy pontosan ugyanazt az értéket kapjuk, mint előbb.159
Úgy látszik tehát, hogy megállapítottuk, a kvantumelmélet időszimmetrikus még akkor is, ha a közönséges unitér U fejlődés mellett az R állapotvektor redukció által leírt nemfolytonos eljárást is figyelembe vesszük. Azonban ez nem így van. A p kvantumos valószínűség – bármelyik úton számolva – az O eredményének (nevezetesen ∣χ〉-nek) valószínűségét írja le, ha O’ eredménye (nevezetesen |ψ’〉 adott. Ez nem szükségképpen egyezik meg O’ eredményének valószínűségével adott O eredmény mellett. Ez utóbbi160 volna az, amit időfordított kvantummechanikánknak valójában adnia kellene. Figyelemre méltó, milyen sok fizikus tételezi fel hallgatólagosan, hogy e két valószínűség azonos. (Magam is bűnös voltam ebben, vö. Penrose 1979b, 584. o.) Ám valószínű, hogy igencsak különbözőek, és a kvantummechanika ténylegesen csak az előbbit adja meg helyesen!
Nézzük meg ezt egy nagyon egyszerű, speciális esetben! Tegyük fel, hogy van egy L lámpánk és egy D fotocellánk (azaz fotondetektorunk)! Legyen L és D között egy félig ezüstözött T tükör, amely valamilyen szöget, mondjuk 45°-osat zár be az L-et és D-t összekötő szakasszal (lásd 8.3. ábra). Tegyük fel, hogy a lámpa véletlenszerű időpontokban fotonokat bocsát ki, és hogy a lámpa felépítése olyan (lehetne például parabolatükröket használni), hogy ezek a fotonok mindig nagyon pontosan megcélozzák D-t. Amikor a fotocella egy fotont észlel, akkor ezt feljegyzi, és feltételezzük, hogy 100%-osan megbízható. Feltehetjük azt is, hogy amikor egy foton kirepül, akkor ezt a tényt feljegyezzük L-nél, megint 100%-os megbízhatósággal. (Ezek az ideális követelmények nincsenek ellentmondásban a kvantummechanikai elvekkel, noha a gyakorlatban nehézségeket okozhat az ilyen hatásfok megközelítése.)
A félig ezüstözött T tükör olyan, hogy a ráeső fotonoknak pontosan a felét visszaveri, a másik felét átengedi. Helyesebb azonban, ha kvantummechanikailag gondolkozunk. A foton hullámfüggvénye beleütközik a tükörbe, és kettéhasad ![]()
az amplitúdója a hullám visszavert részének,
az átengedett résznek. A két részt „együttélőnek” kell tekinteni (a rendes előrehaladó idő leírásban) mindaddig, amíg egy „megfigyelés” nem történik. Abban a pillanatban az együtt élő alternatívák tényleges alternatívákban oldódnak fel – egyikben vagy másikban –, ezek valószínűségeit az amplitúdók (abszolútérték-) négyzetei adják meg, ez most mindkét esetre
Ha elvégezzük a megfigyelést, akkor valóban azt találjuk, hogy mind a foton visszaverődésének, mind az áthaladásának a valószínűsége egyketted.
Nézzük meg, hogyan valósul ez meg kísérletünkben. Tegyük fel, hogy L-nél feljegyezték, hogy kibocsátott egy fotont. A foton hullámfüggvénye a tükörnél kettéhasad, és
amplitúdóval eléri D-t, a fotocella vagy jelez, vagy nem jelez, mindkettőnek egyketted a valószínűsége. A hullámfüggvény másik része eléri a laboratórium falának A pontját (lásd 8.3. ábra), ismét ![]()
amplitúdóval. Ha D nem jelez, akkor úgy kell tekinteni, hogy a foton a falba ütközött az A pontnál. Ha A-ba egy másik fotocellát helyeznénk, akkor az mindig jelezne, amikor D nem jelez – feltéve, hogy L valóban feljegyezte egy foton kibocsátását – és nem jelezne, amikor D jelez. Ebben az értelemben nem szükséges A-ba fotocellát tenni. Pusztán L és D figyelésével következtetni tudunk arra, mit tenne a fotocella A-ban, ha ott volna.
Világosan kell látni, hogyan megy a kvantummechanikai számítás. Feltesszük a kérdést:
„Ha adva van, hogy L jelez, mi a valószínűsége annak, hogy D jelez?”
A válaszhoz megjegyezzük, hogy a foton
amplitúdóval az LTD utat,
amplitúdóval az LTA utat járja be. Négyzetre emeléssel kapjuk, hogy a megfelelő valószínűségek 1/2, illetve 1/2, hogy elérje D-t, illetve A-t. Kérdésünkre a kvantummechanikai válasz ezért
„egyketted”.
Kísérleti úton valóban ezt a választ kapnánk.
Használhatnánk ugyanígy a különc „időfordított” eljárást, hogy megkapjuk ugyanezt a választ. Tegyük fel, hogy feljegyezzük, hogy D jelez. Tekintsük a foton idő hátra hullámfüggvényét, feltéve, hogy végül eléri D-t. Ahogy nyomon követjük visszafelé az időben, a foton visszafelé megy D-ből, amíg eléri az T tükröt. Ennél a pontnál a hullámfüggvény kettéválik,
amplitúdóval eléri az L lámpát, ![]()
amplitúdóval visszaverődik T-nél és egy másik pontot ér el a laboratórium falában, nevezetesen a 8.3. ábra B pontját. Négyzetre emelve megint egykettedet kapunk a két valószínűségre. Ám óvatosan kell megfogalmaznunk, milyen kérdésre válaszolnak ezek a valószínűségek. E két kérdés a következő:
„Ha adott, hogy L jelez, mi a valószínűsége annak, hogy D jelez?”,
éppúgy, mint előbb, és a furcsább kérdés:
„Ha adott, hogy a foton kidobódik a falból B-nél, mi a valószínűsége annak, hogy D jelez?”
Úgy tekinthetjük, hogy e két válasz egyfajta értelemben kísérletileg „korrekt”, noha a második (kibocsátás a falból) következtetés, nem pedig egy tényleges kísérletsorozat eredménye! Ám egyik kérdés sem az időfordítottja annak, amit az előbb kérdeztünk. Ez a következő volna:
„Ha adott, hogy D jelez, mi a valószínűsége annak, hogy L jelez?”
Megjegyezzük, hogy erre a kérdésre a korrekt kísérleti válasz egyáltalán nem „egyketted”, hanem
„egy”.
Ha a fotocella jelez, akkor gyakorlatilag biztos, hogy a foton a lámpából jött, és nem a laboratórium falából! Időfordított kérdésünkre a kvantummechanikai számítás tökéletesen rossz választ adott!
Ennek velejárója az, hogy a kvantummechanika R részének szabályai az ilyen időfordított kérdésekre egyszerűen nem használhatók. Amikor egy múltbéli állapot valószínűségét óhajtjuk kiszámítani egy ismert jövőbéli állapot alapján, akkor teljesen rossz választ kapunk, ha a szabványos R eljárást próbáljuk elfogadni, azaz vesszük egyszerűen a kvantummechanikai amplitúdót és abszolút értékét négyzetre emeljük. A jövőbeli állapotok valószínűségeinek kiszámítása a múltbéliek alapján, csak itt működik ez az eljárás – itt csodálatosan! Számomra ennek alapján világosnak látszik, hogy az R eljárás nem lehet időszimmetrikus (és mellékesen ezért nem származtatható le az időszimmetrikus U eljárásból).
Sokan gondolhatják úgy, hogy az időszimmetriával való ilyen ellentmondásnak az oka az, hogy az érvelésbe valahol becsúszott a termodinamika második főtétele, ez vezetett be időaszimmetriát, amely az amplitúdó négyzetre emelésének eljárásában nincs jelen. Az valóban igaznak látszik, hogy minden fizikai mérőeszköz, amely képes végrehajtani az R eljárást, magával kell hozzon „termodinamikai irreverzibilitást” – ezért amikor mérés történik, az entrópia nő. Azt hiszem, nagyon valószínű, hogy a második főtétel lényeges módon jelen van a mérési folyamatban. Mi több, nem sok fizikai értelme látszik annak, hogy megpróbáljuk időben megfordítani egy kvantummechanikai mérés teljes műveletét, mint az előbb leírt (idealizált) folyamatot, beleértve az összes végrehajtott mérés feljegyzését. Nem foglalkoztam azzal a kérdéssel, milyen messze lehet elmenni egy kísérlet tényleges időbeli megfordításában. Csupán az alkalmazhatóságát vizsgáltam annak a nevezetes kvantummechanikai eljárásnak, amely helyes valószínűségekre jut az amplitúdók abszolút értékeinek négyzetre emelésével. Érdekes tény, hogy ez az egyszerű eljárás a jövő irányában alkalmazható anélkül, hogy a rendszerről bármi más ismeretre szükségünk volna. Valójában az elméletnek része, hogy e valószínűségeket nem tudjuk befolyásolni: a kvantumelméleti valószínűségek teljesen sztochasztikusak! Ha azonban megpróbáljuk az eljárást a múlt irányában alkalmazni (azaz nem jósolni, hanem visszaelemezni), akkor lehangolóan rossz eredményekre jutunk. Felhozhatunk kifogásokat, mentő körülményeket vagy egyéb tényezőket annak magyarázatára, miért nem alkalmazható helyesen az amplitúdó négyzetre emelésének eljárása a múlt irányában, de a tény tény marad. Ilyen kifogásokra a jövő irányában egyszerűen nincs szükség! Az R eljárás, ahogy azt ténylegesen használjuk, nem időszimmetrikus.
159 Ezek a tények valamivel jobban láthatóak a 6. fejezet 119. jegyzetében megadott 〈ψ∣χ〉 skalárszorzat művelet felhasználásával. Az idő előre leírásban a p valószínűség p = ∣〈ψ∣χ〉∣2 = ∣〈χ∣ψ〉∣2, az idő hátra leírásban p = ∣〈χ’∣ψ’〉∣2 = ∣〈ψ’∣χ’〉∣2. Ezek egyenlősége a 〈ψ’∣χ’〉 = 〈ψ∣χ〉 egyenlőségből következik, ami lényegében az „unitér fejlődést” jelenti.
160 Egyes Olvasókat zavarhat a kérdés: mi a valószínűsége egy múltbéli eseménynek, ha adott egy jövőbeli esemény! Lényeges probléma azonban itt nincsen. Képzeljük el a világegyetem teljes történetét téridőtérképen. Hogy megtaláljuk a p esemény valószínűségét, ha adott, hogy q megtörténik, képzeljük el, hogy megvizsgáljuk q minden lehetséges bekövetkezését, és megszámoljuk, ezek hányadrészében következik be p is. Ez a keresett valószínűség. Nem számít, hogy q olyan esemény, amely rendesen időben p-nél később vagy előbb történik meg.
Hawking doboza: kapcsolat a Weyl-féle görbületi hipotézissel?
Lehet, hogy így van, gondolja bizonyára az Olvasó, de mi köze van ennek az egésznek a WGH-hoz vagy a KKG-hez? Igaz, a második főtétel, ahogy ma működik, része lehet az R műveletnek, ám hol van észrevehető szerepe a téridő-szingularitásoknak vagy a kvantumgravitációnak ezekben a folyamatos, „mindennapos” állapotvektor-redukciókban? Hogy e kérdéshez eljussunk, le fogok írni egy szokatlan „gondolatkísérletet”, amelyet eredetileg Stephen Hawking javasolt, bár ő más célból tette ezt, mint amiért én most előhozom.
Képzeljünk el egy hatalmas méretű, zárt dobozt! Falai teljesen visszaverőek, áthatolhatatlanok bármilyen hatás számára. Nem mehet keresztül rajta semmilyen anyagi objektum, sem elektromágneses jel, sem neutrínó vagy bármi más. Mindennek vissza kell verődnie rajta, akár kívülről érkezik, akár belülről. Még a gravitáció hatásai sem juthatnak át. Nincs olyan anyag, amelyből ilyen falakat lehetne építeni. A „kísérletet”, amelyet leírok, senki nem tudná ténylegesen végrehajtani. (Nem is akarná, amint látni fogjuk!) Nem ez a lényeg. Egy gondolatkísérletben általános elveket igyekszünk feltárni olyan kísérlet elméleti vizsgálata útján, amelyet elvégezhetnénk. A technikai nehézségeket figyelmen kívül hagyjuk, feltéve, hogy nem befolyásolják a vizsgált általános elveket. (Emlékezzünk Schrödinger macskájára a 6. fejezetből.) Esetünkben a doboz falai elkészítésének nehézségeit tisztán „technikaiaknak” tekintjük, ezért nem törődünk velük.
A dobozban valamilyen fajtájú anyag van nagy mennyiségben. Nem sokat számít, hogy mi ez az anyag. Bennünket csak az M teljes tömeg érdekel, amely nagyon nagy kell legyen, és a tömeget tartalmazó nagy doboz V térfogata. Mit csináljunk drágán elkészített dobozunkkal és teljesen érdektelen tartalmával? A kísérlet az elképzelhető legunalmasabb kísérlet. Hagyjuk a dobozt érintetlenül – mindörökre!
A bennünket foglalkoztató kérdés a doboz tartalmának végső sorsa. Entrópiájának a termodinamika második főtétele szerint növekednie kell. Növekednie mindaddig, amíg el nem éri a maximális értéket, amikor az anyag „hőmérsékleti egyensúlyba” jut. Ettől kezdve semmi nem történne, ha nem lennének „ingadozások”, amelyek során átmenetileg a hőmérsékleti egyensúlytól (viszonylag) nagy eltérések lépnek fel. Feltételeztük, hogy M elég nagy és V megfelelően választott (nagyon nagy, de nem túl nagy), ezért amikor a „hőmérsékleti egyensúly” beáll, az anyag legnagyobb része egy fekete lyukká omlott össze, kívüle csak egy kis anyag és sugárzás van – amely egy ún. (nagyon hideg!) „hőfürdőt” képez, ebbe merül a fekete lyuk. A határozottság kedvéért válasszuk M-et a naprendszer tömegének, V-t a Tejút méretének! Ekkor a „fürdő” hőmérséklete csak kb. 10–7 fok volna az abszolút nulla felett!
Hogy világosabban megértsük ennek az egyensúlynak és az ingadozásoknak a természetét, hadd idézzem fel a fázistér fogalmát, amellyel az 5. és 7. fejezetekben találkoztunk, különösen az entrópia meghatározásával kapcsolatban. A 8.4. ábrán vázlatos képét látjuk a Hawking-doboz tartalma egész P fázisterének. Emlékezzünk rá, hogy a fázistér egy nagy dimenziószámú tér, amelynek minden egyes pontja a vizsgált rendszernek – most a doboz tartalmának – egy lehetséges teljes állapotát jelképezi. Így P minden egyes pontja megadja a dobozban lévő összes részecske helyzetét és impulzusát, ezzel együtt az összes szükséges információt a téridő-geometriáról a dobozon belül. P-nek B résztartománya a 8.4. ábra jobb oldalán azokat az állapotoknak az összességét ábrázolja, amelyekben a dobozban van egy fekete lyuk (benne azokat az állapotokat is, amelyekben egynél több fekete lyuk van), míg az A résztartomány a bal oldalon azoknak az állapotoknak az összességét, amelyekben nincs fekete lyuk. Fel kell tételeznünk, hogy mindkét résztartomány tovább osztódik kis tartományokra a „durva szemcsézésnek” megfelelően, ami szükséges az entrópia pontos definíciójához (vö. 7.3. ábra), de ezek a részletek nem érdekelnek bennünket. Most mindössze azt kell megjegyeznünk, hogy e tartományok legnagyobbja – amely a hőmérsékleti egyensúlyt képviseli egy fekete lyukkal – a B fő része, míg A (valamivel kisebb) fő része azt képviseli, ami hőmérsékleti egyensúlynak látszik, kivéve azt, hogy fekete lyuk nincs jelen.
Emlékezzünk arra, hogy minden fázistérben megadható egy nyílmező (vektormező), amely a fizikai rendszer időbeli fejlődését ábrázolja (lásd 5. fejezet, valamint az 5.11. ábra). Ezért hogy megtudjuk, mi fog történni rendszerünkben, egyszerűen követnünk kell a nyilakat P-ben (lásd 8.5. ábra). Egyes nyilak átvezetnek az A tartományból a B tartományba. Ez akkor következik be, amikor az anyag gravitációs összehúzódása során először képződik egy fekete lyuk. Vannak-e nyilak, amelyek visszavezetnek a B tartományból az A-ba? Igen, vannak, de csak akkor, ha figyelembe vesszük a Hawking-párolgás jelenségét, amelyre korábban hivatkoztunk (lásd 7. és 8. fejezet). A szigorú, klasszikus általános relativitáselmélet szerint a fekete lyukak csak elnyelni tudják a dolgokat, kibocsátani nem. Azonban a kvantummechanikai jelenségeket figyelembe véve Hawking (1975) meg tudta mutatni, hogy a fekete lyukaknak a kvantumszinten képeseknek kellene lenniük kibocsátani dolgokat, ez a folyamat a Hawking-sugárzás. (Ez a „virtuális párkeltés” kvantumos folyamata útján következik be, részecskék és antirészecskék – átmenetileg – folyamatosan képződnek a vákuumból, rendesen csupán szétsugároznak közvetlenül a keletkezés után, nyomot nem hagynak. Amikor azonban egy fekete lyuk jelen van, az a pár egyik részecskéjét „elnyelheti”, még mielőtt a szétsugárzás bekövetkezne, a másik kiszökhet a lyukból. A kiszökő részecskék képezik a Hawking-sugárzást.) A dolgok rendes meneténél e Hawking-sugárzás nagyon parányi. Azonban a hőmérsékleti egyensúly állapotában az energia mennyisége, amelyet a fekete lyuk a Hawking-sugárzásban veszít, pontosan ellensúlyozza azt az energiát, amelyet más „termikus részecskék” elnyelésével szerez, ha ezek történetesen a fekete lyuk „hőfürdőjében” keringenek. Alkalmanként, egy „ingadozásban” a lyuk egy kissé sokat bocsáthat ki, vagy egy kissé keveset nyelhet el, ezáltal energiát veszíthet. Ekkor (Einstein E = mc2 egyenlete szerint) tömeget veszít, és a Hawking-sugárzás szabályai szerint parányival forróbb lesz. Nagyon-nagyon ritkán, amikor az ingadozás elég nagy, az is lehetséges, hogy a fekete lyuk egyre forróbb lesz, egyre több energiát veszít, egyre kisebb lesz, míg végül egy heves robbanásban (feltehetően) teljesen eltűnik! Amikor ez megtörténik (feltéve, hogy a dobozban nincs más fekete lyuk), akkor áll elő az a helyzet, hogy a P fázistérben átmegyünk a B tartományból az A-ba, tehát valóban vannak nyilak B-ből A-ba!
Ezen a ponton egy megjegyzést kell tennem arról, mit értünk „ingadozás” alatt. Emlékezzünk a durvaszemcsés tartományokra, amelyeket az előző fejezetben vizsgáltunk. Az egyazon tartományhoz tartozó fázistérpontokat egymástól (makroszkopikusan) „megkülönböztethetetlennek” tekintjük. Az entrópia azért növekszik, mert a nyilakat követve az idő haladtával egyre nagyobb és nagyobb tartományokba jutunk. A fázispont végül mind közt a leghatalmasabb tartományba kerül, amely a hőmérsékleti egyensúlynak (a maximális entrópiának) felel meg. Ez azonban csak egy pontig igaz. Ha elég sokáig várunk, akkor a fázispont végül is megtalál egy kisebb tartományt, és ekkor az entrópia csökken. Ez rendesen nem tart (viszonylag) sokáig, az entrópia hamarosan ismét visszaáll az előbbi értékre, amint a fázistérpont visszalép a legnagyobb tartományba. Ez egy ingadozás, az entrópia pillanatnyi csökkenésével. Az entrópia rendszerint nem nagyon sokkal csökken, de nagyon-nagyon ritkán bekövetkezik egy hatalmas ingadozás, és az entrópia lényegesen csökkenhet – és esetleg jelentős ideig alacsony marad.
Ez a fajta dolog szükséges ahhoz, hogy a Hawking-párolgás révén a B tartományból az A tartományba jussunk. Nagyon nagy ingadozásra van szükség, mert a nyilak mentén egy kis tartományon keresztül vezet az út B-ből A-ba. Hasonlóképpen, amikor fázistérpontunk A fő tartományában fekszik (amely a hőmérsékleti egyensúly állapotát képviseli fekete lyuk nélkül), akkor is nagyon hosszú idő telik el, míg bekövetkezik egy gravitációs összeomlás, és a pont átmegy B-be. Megint egy nagy ingadozásra van szükség. (A hőmérsékleti sugárzás nem viseli el könnyen a gravitációs kollapszust!)
Több nyíl vezet-e A-ból B-be, mint B-ből A-ba, vagy egyenlő a kétféle nyilak száma? Ez fontos kérdés számunkra. A kérdést másképp fogalmazva: „könnyebb-e” a természetnek fekete lyukat létrehozni termikus részecskék gravitációs összehúzásával, mint megszabadulni egy fekete lyuktól Hawking-sugárzással, vagy a kettő egyformán „nehéz”? Szigorúan szólva nem a nyilak „száma” az érdekes, hanem a fázistér-térfogat áramlási sebessége. Gondoljuk azt, hogy a fázistér meg van töltve valamilyen (sokdimenziójú) összenyomhatatlan folyadékkal. A nyilak e folyadék áramlását jelképezik. Emlékezzünk vissza a Liouville-tételre, amelyet az 5. fejezetben beszéltünk meg. Ez a tétel azt állítja, hogy a fázistér térfogata az áramlás során megmarad, ami azt jelenti, hogy folyadékunk valóban összenyomhatatlan! A Liouville-tétel, úgy látszik, azt mondja nekünk, hogy az A-ból B-be való áramlás egyenlő kell legyen a B-ből A-ba való áramlással, mert a fázistér-„folyadék”, lévén összenyomhatatlan, nem gyűlhet össze egyik vagy másik oldalon. Így úgy látszik, hogy pontosan egyenlő „nehéz” kell legyen fekete lyukat építeni hőmérsékleti sugárzásból, mint lerombolni azt!
Ez volt Hawking saját következtetése, noha ő némileg eltérő meggondolások alapján jutott erre. Fő érvelése az volt, hogy a problémában szerepet játszó minden alapvető fizika (általános relativitáselmélet, termodinamika, a kvantumelmélet szabványos unitér eljárásai) időszimmetrikus, ezért ha visszafelé járatjuk az órát, ugyanazt a választ kell kapnunk, mint amit az előre járatásnál. Ez egyszerűen csak P nyilainak megfordítását jelenti. Valóban ebből az érvelésből is következne, hogy pontosan ugyanannyi nyílnak kell vezetnie A-ból B-be, mint amennyinek B-ből A-ba, feltéve, hogy a B tartomány időmegfordítottja újra a B tartomány (és ugyanúgy az A tartományé az A tartomány). Ez a kikötés egyenértékű Hawking figyelemre méltó javaslatával, amely szerint a fekete lyukak és időmegfordítottjaik, a fehér lyukak fizikailag azonosak! Érvelése az volt, hogy időszimmetrikus fizikában a hőmérsékleti egyensúly állapotának is időszimmetrikusnak kellene lennie. Nem óhajtok elmerülni e meglepő lehetőség részletes vizsgálatában. Hawking elképzelése szerint a kvantummechanikai Hawking-sugárzást valahogyan a fekete lyuk klasszikus „anyagelnyelése” időmegfordítottjának lehetne tekinteni. E javaslat, bár szellemes, komoly elméleti nehézségekbe ütközik; én magam nem hiszem, hogy életképessé tehető.
A javaslat mindenesetre nem igazán fér össze azokkal az elképzelésekkel, amelyeket felvetettem. Úgy érveltem, hogy míg a fekete lyukaknak létezniük kell, a fehér lyukaknak a Weyl-féle görbületi hipotézis miatt ez tilos! A WGH időaszimmetriát vezet be a meggondolásba, amit Hawking nem vett figyelembe. Rá kell mutatnunk arra, hogy mert a fekete lyukak és téridő-szingularitásaik valóban nagyon komoly részei annak, ami a Hawking-doboz belsejében történik, ezért az ilyen szingularitások viselkedését előíró ismeretlen fizika biztosan szerephez jut. Hawking arra az álláspontra helyezkedik, hogy az ismeretlen fizikának egy időszimmetrikus kvantumgravitáció-elméletnek kell lennie, míg én azt állítom, hogy az az időaszimmetrikus KKG! Nézetem szerint a KKG egyik fő velejárója a WGH kell legyen (és következésképp a termodinamika második főtétele jelenleg ismert formájában), ezért meg kell próbálnunk kideríteni, milyen következményei vannak a WGH-nak jelenlegi problémánk szempontjából.
Nézzük meg, hogyan befolyásolja a WGH P-beli „összenyomhatatlan folyadékunk” áramlását. Egy feketelyuk-szingularitás hatása a téridőben az, hogy elnyel és megsemmisít minden anyagot, amely beleütközik. Ami jelen esetünkben még fontosabb: információt semmisít meg! Ennek hatása P-ben az, hogy egyes áramvonalak összeolvadnak (lásd a 8.6. ábrát). Két, korábban különböző állapot azonossá válhat, mihelyt az őket megkülönböztető információ megsemmisül. Amikor P-ben áramvonalak olvadnak egybe, akkor a Liouville-tétel ténylegesen megsérül. „Folyadékunk” többé nem összenyomhatatlan, hanem a B tartományban folyamatosan megsemmisül!
Most, úgy látszik, bajba jutottunk. Ha „folyadékunk” folyamatosan megsemmisül a B tartományban, akkor A-ból B-be több áramvonal kell menjen, mint B-ből A-ba – tehát „könnyebb” létrehozni egy fekete lyukat, mint megsemmisíteni! Ennek valóban volna értelme, ha nem úgy állna, hogy most több „folyadék” folyik ki az A tartományból, mint amennyi oda belép. Fekete lyukak az A tartományban nincsenek – a fehér lyukak létét a WGH kizárja –, ezért a Liouville-tételnek az A tartományban teljesülnie kellene! Ám úgy látszik, az A tartományban szükségünk van valamilyen „folyadékkeltési” módra, hogy pótoljuk a B-beli veszteséget. Milyen mechanizmus szolgálhat ott az áramvonalak számának növelésére? Úgy látszik, azt követeljük, hogy ugyanannak az állapotnak olykor egynél több lehetséges folytatása lehessen (azaz az áramvonalak szétváljanak). Egy fizikai rendszer jövőbeli fejlődésének ez a fajta bizonytalansága kvantumelmélet „szagú” – az R részre emlékeztet. Lehetséges-e, hogy valamilyen értelemben R a „WGH-érem másik oldala”? Ahogy a WGH okozza az áramvonalak egybeolvadását B-ben, a kvantummechanikai R eljárás okozza szétválásukat. Azt állítom, hogy az állapotvektor-redukció (R) objektív kvantummechanikai folyamata az, ami az áramvonalak szétválását okozza, így egyenlíti ki pontosan az áramvonalak WGH okozta egybeolvadását (8.6. ábra)!
Hogy ilyen szétválás (bifurkáció) bekövetkezzék, ahhoz, mint már láttuk, R-nek időaszimmetrikusnak kell lennie: emlékezzünk kísérletünkre a lámpával, fotocellával és félig ezüstözött tükörrel. Amikor a lámpa kibocsát egy fotont, a folyamatnak két (egyenlően valószínű) alternatívája van: a foton vagy a fotocellát éri el, és az jelez, vagy a falat az A pontban, és a fotocella nem jelez.
E kísérlet fázisterében egy áramvonal ábrázolja a foton kibocsátását, ez válik ketté: az egyik azt a helyzetet írja le, amikor a fotocella megszólal, a másik azt, amikor nem szólal meg. Ez valódi bifurkáció, mert csak egy megengedett bemenet van és két lehetséges kimenet. A másik bemenet, amelyet figyelembe kellett volna venni, az a lehetőség, hogy a fotont a laboratórium fala bocsátotta ki a B pontban, így volna két bemenet és két kimenet. Ám ezt az alternatív bemenetet kizártuk a termodinamika második főtételével való összeférhetetlenség alapján – azaz az itt kifejtett nézőpont szerint, amely a fejlődést a múltba követi vissza, és amelynek végén a WGH áll.
Szeretném újból megismételni, hogy az általam kifejtett nézőpont nem igazán „hagyományos” – noha egyáltalán nem világos számomra, mit mondana a „hagyományos” fizikus, hogy az összes felmerülő problémát megoldja. (Gyanítom, hogy nem sokan törték sokat a fejüket ezeken a kérdéseken.) Számos különböző véleményt hallottam. Időnként például egyes fizikusok azt állítják, hogy a Hawking-sugárzás soha nem tüntet el teljesen egy fekete lyukat, mindig marad valamilyen kis „rög”. (E nézet szerint nem vezetnek nyilak B-ből A-ba!) Ez tulajdonképpen csak kevéssé különbözik érvelésemtől (valójában megerősíti). Következtetéseim azonban elkerülhetők, ha azt posztuláljuk, hogy a P fázistér teljes térfogata végtelen, ám ez ellentmondásban van bizonyos, a fekete lyukak entrópiájával és egy korlátos (kvantumos) rendszer fázisterének természetével kapcsolatos, meglehetősen alapvető elképzelésekkel; következtetéseim elkerülésének más technikai módjai, amelyekről hallottam, sem tűnnek elfogadhatóbbaknak. Egy lényegesen komolyabb ellenvetés: a Hawking-doboz elkészítésében fellelhető idealizációk túlságosan nagyok, és az a feltevés, hogy ilyet lehet építeni, bizonyos elvi kérdéseknek mond ellent. Ebben magam is bizonytalan vagyok, de hajlok arra, hogy a szükséges idealizációk valójában lenyelhetőek!
Van végül egy komoly pont, amelyet elkendőztem. A vizsgálatot azzal a feltételezéssel kezdtem, hogy van egy klasszikus fázisterünk – a Liouville-tétel a klasszikus fizikára érvényes. Ám ezután a Hawking-sugárzás kvantumos jelenségével kellett foglalkoznunk. (És a kvantumelméletre ténylegesen szükség van P véges térfogata és véges dimenziószáma érdekében is.) Amint azt a 6. fejezetben láttuk, a fázistér kvantumos változata a Hilbert-tér, ezért a gondolatmenetben a fázistér helyett feltételezhetően végig a Hilbert-teret kellene használnunk. A Hilbert-térben megvan a Liouville-tétel analogonja. Abból származik, amit az U időfejlődés „unitér” természetének neveznek. Lehet, hogy egész érvelésem elmondható a klasszikus fázistér helyett a Hilbert-térrel, ám nehéz látni, hogyan vizsgáljuk ilyen módon a fekete lyukak téridő-geometriájának klasszikus jelenségeit. Véleményem az, hogy a helyes elmélethez sem a Hilbert-tér, sem a klasszikus fázistér nem megfelelő, hanem egy eddig nem ismert típusú matematikai teret kellene használni, amely a kettő között van valahol. Érvelésemet ezek szerint csak heurisztikus szintűnek kell venni, és inkább csak szuggesztív, mintsem eldöntő. Mindazonáltal úgy gondolom, erősen amellett szól, hogy a WGH és R mély kapcsolatban áll egymással, és hogy következésképpen R valóban kvantumgravitációs hatás kell legyen.
Megismétlem következtetéseimet: azt a javaslatot vetem föl, hogy a kvantummechanikai állapotvektor-redukció valójában a WGH-érem másik oldala. E nézet szerint keresett „korrekt kvantumgravitáció”- elméletünk két fő velejárója a WGH és az R. A WGH hatása az áramvonalak egybefolyása a fázistérben, míg R hatása az áramvonalak az előbbit pontosan egyensúlyozó szétágazása. Mindkét folyamat szoros kapcsolatban áll a termodinamika második főtételével.
Megjegyzem, hogy az áramvonalak egybefolyása kizárólag a B tartományban megy végbe, míg a szétágazás történhet vagy A-ban, vagy B-ben. Emlékezzünk rá, hogy A képviseli a fekete lyukak hiányát, így az állapotvektor-redukció valóban megtörténhet, amikor fekete lyukak nincsenek. Világos, hogy nincs szükség a laboratóriumban egy fekete lyukra ahhoz, hogy R végrehajtódjék (mint az előbb tárgyalt fotonkísérletünkben). Csak az általános egyensúly a lényeges a lehetséges dolgok között, amelyek egy helyzetben megtörténhetnek. A kifejtett nézőpont szerint a determinizmus hiányának csak a fekete lyukak képződésének (és következésképp az információ megsemmisülésének) lehetőségét kell egyensúlyoznia a kvantumelméletben!
...
Megismétlem következtetéseimet: azt a javaslatot vetem föl, hogy a kvantummechanikai állapotvektor-redukció valójában a WGH-érem másik oldala. E nézet szerint keresett „korrekt kvantumgravitáció”- elméletünk két fő velejárója a WGH és az R. A WGH hatása az áramvonalak egybefolyása a fázistérben, míg R hatása az áramvonalak az előbbit pontosan egyensúlyozó szétágazása. Mindkét folyamat szoros kapcsolatban áll a termodinamika második főtételével.- A tünékeny logikai kapcsolat.
Mikor redukálódik az állapotvektor?
Tegyük fel, az előző érvelés alapján elfogadjuk, hogy az állapotvektor redukciója végül is valamiféle gravitációs jelenség lehet. Határozottabbá lehet-e tenni R és a gravitáció kapcsolatát? E szemlélet alapján mikor következik be ténylegesen az állapotvektor redukciója?
Szeretnék először rámutatni, hogy még a kvantumgravitáció elméletének „hagyományosabb” megközelítéseinél is komoly technikai nehézségek lépnek fel, amikor az általános relativitás elveit a kvantumelmélet szabályaival egyeztetik össze. Ezek a szabályok (főként az impulzus értelmezése, amely szerint a hely szerinti differenciálhányadosként jelenik meg a Schrödinger-egyenletben, lásd 6. fejezet) határozottan nem jól illenek össze a görbült téridő-geometria elképzeléseivel. Az én nézetem az, hogy amint „jelentőssé” válik a téridő görbülete, a kvantumos lineáris szuperpozíció szabályainak el kell romlaniuk. Ez az a hely, ahol a potenciálisan alternatív állapotok komplex amplitúdós szuperpozíciói átadják helyüket a valószínűségekkel súlyozott tényleges alternatíváknak – és az alternatívák egyike ténylegesen megvalósul.
Mit értek „jelentős” mértékű görbületen? Azt a szintet, amikor a bevezetett görbület nagysága hozzávetőlegesen az egy graviton161 szintet éri el, vagy annál nagyobb. (Emlékezzünk rá, hogy a kvantumelmélet szabályai szerint az elektromágneses mező „fotonoknak” nevezett egységekben „kvantált”. Amikor a mezőt különálló frekvenciákra bontjuk szét, a ν frekvenciájú rész csak egész számú fotont tartalmazhat, amelyek egyenkénti energiája hν. Feltehetően hasonló szabályok érvényesek a gravitációs mezőre.) Egy graviton a görbület legkisebb egysége, amit a kvantumelmélet megenged. Az elképzelés az, hogy amint e szintet elérjük, a lineáris szuperpozíciónak az U eljárás szerinti közönséges szabályai a gravitonokra alkalmazva módosulnak, és fellép valamiféle időaszimmetrikus „nemlineáris instabilitás”. Ekkor már nem az örökké „együttélő” komplex lineáris szuperpozícióink lesznek, hanem az egyik alternatíva győzedelmeskedik, és a rendszer „beugrik” ebbe az állapotba. Az alternatívák közötti választás véletlenszerű, vagy esetleg van valami mélyebb megalapozása. A valóság azonban most már az egyik vagy a másik. Az R eljárás végbement.
Megjegyezzük, hogy ezen elképzelés szerint az R eljárás teljesen objektív és spontán módon következik be, minden emberi beavatkozástól függetlenül. Az elképzelés az, hogy az „egygraviton-szintnek” kényelmesen kell beilleszkednie az atomok, molekulák stb. „kvantumszintje” – ahol jól működnek a közönséges kvantumelmélet lineáris szabályai (U) – és mindennapos tapasztalataink „klasszikus szintje” közé. Milyen „nagy” az egygraviton-szint? Hangsúlyoznunk kell, hogy ez nem igazán a fizikai méret kérdése: sokkal inkább a tömeg- és energiaeloszlásé. Láttuk, hogy a kvantumos interferenciajelenségek nagy távolságokon is felléphetnek, feltéve hogy az energia nem nagy. (Emlékezzünk a foton önmagával való interferenciájára és Clausen és Aspect EPR-kísérletére.) A jellegzetes kvantumgravitációs tömegskála a Planck-tömeg néven ismert
mP = 10–5 gramm
(közelítőleg). Ez látszólag sokkal nagyobb a kívántnál, minthogy jóval kisebb tömegű objektumok, például a porszemek klasszikus viselkedése közvetlenül észlelhető. (Az mP tömeg valamivel kisebb egy bolha tömegénél.) Nem hiszem azonban, hogy az egygravitonos feltétel ennyire durván érvényes. Megpróbálok egy kicsivel világosabb lenni, ám az írás idején még sok a homály és a kétség arra vonatkozóan, hogyan kell e feltételt pontosan alkalmazni.
Tekintsük először egy részecske megfigyelésének nagyon közvetlen módját, nevezetesen a Wilson-féle ködkamra használatát. Van egy párával teli kamránk éppen a cseppekké való kicsapódás küszöbén. Amikor egy gyorsan mozgó, töltött részecske, amely mondjuk egy, a kamrán kívül elhelyezett radioaktív atom bomlásában keletkezett, belép a kamrába, akkor a gőzön való áthaladása során egyes, a pályájához közeli atomokat ionizál (elektronokat szakít le róluk, így azok töltötté válnak). Ezek az ionizált atomok lesznek a központok, amelyek körül kis cseppek csapódnak ki a gőzből. A cseppek által kialakított nyomot a kísérletező közvetlenül megfigyelheti (8.7. ábra).
Mi most ennek a kvantummechanikai leírása? Radioaktív atomunk bomlásának pillanatában kibocsát egy részecskét. E kibocsátott részecske sokféle lehetséges irányban mozoghat. Lesz egy amplitúdója ennek az iránynak, lesz egy annak, és lesz minden más iránynak is, mindezek együtt jelentkeznek kvantumos lineáris szuperpozícióban. E szuperponált alternatívák összessége egy, az elbomló atomból kifutó gömbhullámot képez: a kibocsátott részecske hullámfüggvényét. Amint az összes lehetséges részecskenyom belép a ködkamrába, ionizált atomok egy füzérével kapcsolódik össze, melyek mindegyike kicsapódási középpontként kezd működni. Az ionizált atomok ezen összes különböző lehetséges füzérei szintén kvantumos lineáris szuperpozícióban kell együttéljenek, ezért most van egy lineáris szuperpozíciónak kicsapódó cseppek nagyszámú különböző füzéréből. E komplex kvantumos lineáris szuperpozíció valamelyik fejlődési fokozatában tényleges alternatívák valós valószínűségsúlyozott együttesévé válik, amint a komplex amplitúdósúlyokat az R eljárás szerint abszolútérték-négyzeteik váltják fel. A tapasztalat valódi fizikai világában csak egyikük valósul meg, és ezt a speciális alternatívát figyeli meg a kísérletező. Az általam javasolt nézőpont szerint ez a lépés akkor következik be, amint a különböző alternatívák gravitációs mezői közötti különbség eléri az egygraviton-szintet.
Mikor történik ez meg? Nagyon durva számítás162 szerint, ha csupán egy teljesen egyenletes gömb alakú csepp volna, úgy az egygravitonos lépcső akkor jelentkezne, amikor a csepp nagyjából mP egy századára nőne, ami egy tízmilliomod gramm. Sok bizonytalanság van e számításban (elvi nehézségeket is beleértve), és a méret a kényelmesnél kicsit nagyobb, de nem teljesen ésszerűtlen. Később remélhetőleg lesznek pontosabb eredmények is, és lehetséges lesz a cseppek egész füzérét kezelni, nem csak egyetlen cseppet. Jelentős különbségeket eredményezhet annak figyelembevétele is, hogy a cseppek nem teljesen egyenletesek, hanem nagyon nagyszámú parányi atomból épülnek fel. Mi több, magát az „egygraviton-feltételt” is matematikailag lényegesen pontosabbá kell tenni.
A fenti helyzetben azt tekintettem át, mi lehet egy kvantumos folyamat (egy radioaktív atom bomlása) tényleges megfigyelése, amikor is a kvantumos jelenségeket felnagyítjuk addig a pontig, amelynél a különböző kvantum alternatívák különböző, közvetlenül megfigyelhető makroszkopikus alternatívákat hoznak létre. Nézetem szerint R akkor is objektíven mehetne végbe, amikor ilyen látható nagyítás nincs jelen. Tegyük fel, hogy részecskénk nem ködkamrába lép be, hanem egy nagy doboz olyan sűrűségű gázba (vagy folyadékba), hogy gyakorlatilag biztosan ütközik a gáz nagyszámú atomjával, vagy másképp megzavarja azokat. Tekintsünk a részecske számára csupán két alternatívát mint a kezdeti komplex lineáris szuperpozíció részeit: lehet, hogy egyáltalán nem lép be a dobozba, vagy belép egy speciális út mentén, és ütközik a gáz valamelyik atomjával. A második esetben ez a gázatom nagy sebességgel mozog tovább úgy, ahogy máskülönben, ha a részecskével nem ütközött volna, nem tenné, és ezután egy másik atommal fog ütközni. Ekkor már két atom mozog ilyen különleges módon, és hamarosan az atomi mozgások egész láncolata fejlődik ki a gázban, amely nem alakulna ki, ha a részecske nem lépne be a dobozba (8.8. ábra). Hamarosan a gáz minden atomja megzavarodik ettől a mozgástól.
Gondoljuk most meg, hogyan kellene leírnunk ezt kvantummechanikailag? Kezdetben csak az eredeti részecskénk különböző helyzetei jelennek meg a komplex lineáris szuperpozícióban – mint a részecske hullámfüggvényének részei. Ám hamarosan a gáz összes atomját be kell vennünk. Tekintsük a részecske által választható két út komplex szuperpozícióját, az egyiknél belép a dobozba, a másiknál nem. A szabványos kvantummechanika szerint ki kell terjesztenünk e szuperpozíciót a gáz összes atomjára: két olyan állapotot kell szuperponálnunk, ahol az egyik állapotban az összes gázatom elmozdult a másikban elfoglalt helyzetéből. Tekintsük most az egyedi atomok összességének gravitációs mezői közötti különbséget. Noha a gáz egészének eloszlása tulajdonképpen azonos a két szuperponálandó állapotban (és az együttes gravitációs mezők gyakorlatilag azonosak), ha az egyik mezőt levonjuk a másikból, akkor egy (nagyon oszcilláló) különbségmezőt kapunk, amely nyugodtan lehet „jelentős” abban az értelemben, ahogy itt beszélünk róla – könnyen felülmúlhatja az egygraviton-szintet. Amint ez bekövetkezik, megtörténik az állapotvektor-redukció: a rendszer tényleges állapotában a részecske vagy belépett a gázba, vagy nem. A komplex lineáris szuperpozíció statisztikusan súlyozott alternatívákra redukálódik, és ténylegesen csak egyikük valósul meg.
Mindez csak csírája egy elképzelésnek, amelyet a nagyon keresett új elméletnek gondolok.163 Bármely teljesen kielégítő rendszer, úgy vélem, nagyon radikális új elképzeléseket kell tartalmazzon a téridő-geometria természetéről, közöttük valószínűleg egy lényegesen nemlokális leírást.164 E hitem egyik legkényszerítőbb oka az EPR-típusú kísérletekből ered (lásd 6. fejezet), amelyekben egy „megfigyelés” egy terem egyik sarkában az állapotvektor egyidejű redukcióját eredményezheti a másikban. Az állapotvektor-redukció egy olyan teljesen objektív elméletének felépítése, amely összhangban van a relativitás szellemével, igen komoly kihívás, mert az „egyidejűség” fogalma idegen a relativitáselmélettől, minthogy függvénye a megfigyelő mozgásának. Véleményem az, hogy a fizikai valóságról alkotott jelenlegi képünk, különösen az idő természetét illetően, megérett a nagy átalakításra – talán még nagyobbra, mint amilyet a mai relativitáselmélet és kvantummechanika már magával hozott.
Vissza kell térnünk az eredeti kérdésre. Hogyan kapcsolódik mindez ahhoz a fizikához, amely agyunk működését szabályozza? Mi köze lehet ennek gondolatainkhoz és érzéseinkhez? Hogy megkíséreljünk valamilyen választ adni, először meg kell vizsgálnunk, milyen az agyunk felépítése. Utána majd visszatérek ahhoz, amit az alapvető kérdésnek gondolok: miféle új fizikai hatás lép be valószínűen, amikor tudatosan gondolkodunk vagy érzékelünk?
161 Meg kell engednünk, hogy ezek ún. longitudinális gravitonok legyenek – a „virtuális” gravitonok, amelyek egy sztatikus gravitációs mezőt alkotnak. Sajnos az ilyen dolgok világos és „invariáns” matematikai meghatározásánál elméleti nehézségek lépnek föl.
162 Eredeti durva próbálkozásaimat ennek az értéknek kiszámítására Abhay Ashtekar jelentősen megjavította, itt most az ő eredményét használom (lásd Penrose 1987a). Ő azonban hangsúlyozta, hogy egyes feltevésekben, amelyeket használni kényszerülünk, nagyfokú önkényesség van, ezért megfelelő óvatosságot kell tanúsítanunk a pontos tömegérték elfogadásánál.
163 Az irodalomban időről időre változatos próbálkozások jelennek meg az állapotvektor-redukció objektív elméletének felállítására. A legfontosabbak Károlyházy (1974), Károlyházy, Frenkel és Lukács (1986), Komar (1969), Pearle (1985, 1988), Ghirardi, Rimini és Weber (1986).
164 Az évek során magam is megpróbáltam kidolgozni a téridő egy nemlokális elméletét, főként más irányokból, az ún. „twisztorelmélettől” ösztönözve (lásd Penrose és Rindler 1986, Huggett és Tod 1985, Ward és Wells 1989). Ám ebből az elméletből a legjobb indulat mellett is hiányolnunk kell lényeges alkotórészeket, és nem volna helyénvaló, ha itt most ennek vizsgálatával foglalkoznánk.
1./ Az én nézetem az, hogy amint „jelentőssé” válik a téridő görbülete, a kvantumos lineáris szuperpozíció szabályainak el kell romlaniuk. Ez az a hely, ahol a potenciálisan alternatív állapotok komplex amplitúdós szuperpozíciói átadják helyüket a valószínűségekkel súlyozott tényleges alternatíváknak – és az alternatívák egyike ténylegesen megvalósul.
Mit értek „jelentős” mértékű görbületen? Azt a szintet, amikor a bevezetett görbület nagysága hozzávetőlegesen az egy graviton161 szintet éri el, vagy annál nagyobb. (Emlékezzünk rá, hogy a kvantumelmélet szabályai szerint az elektromágneses mező „fotonoknak” nevezett egységekben „kvantált”. Amikor a mezőt különálló frekvenciákra bontjuk szét, a ν frekvenciájú rész csak egész számú fotont tartalmazhat, amelyek egyenkénti energiája hν. Feltehetően hasonló szabályok érvényesek a gravitációs mezőre.) Egy graviton a görbület legkisebb egysége, amit a kvantumelmélet megenged. Az elképzelés az, hogy amint e szintet elérjük, a lineáris szuperpozíciónak az U eljárás szerinti közönséges szabályai a gravitonokra alkalmazva módosulnak, és fellép valamiféle időaszimmetrikus „nemlineáris instabilitás”. Ekkor már nem az örökké „együttélő” komplex lineáris szuperpozícióink lesznek, hanem az egyik alternatíva győzedelmeskedik, és a rendszer „beugrik” ebbe az állapotba. Az alternatívák közötti választás véletlenszerű, vagy esetleg van valami mélyebb megalapozása. A valóság azonban most már az egyik vagy a másik. Az R eljárás végbement.
Megjegyezzük, hogy ezen elképzelés szerint az R eljárás teljesen objektív és spontán módon következik be, minden emberi beavatkozástól függetlenül. Az elképzelés az, hogy az „egygraviton-szintnek” kényelmesen kell beilleszkednie az atomok, molekulák stb. „kvantumszintje” – ahol jól működnek a közönséges kvantumelmélet lineáris szabályai (U) – és mindennapos tapasztalataink „klasszikus szintje” közé. Milyen „nagy” az egygraviton-szint? Hangsúlyoznunk kell, hogy ez nem igazán a fizikai méret kérdése: sokkal inkább a tömeg- és energiaeloszlásé. Láttuk, hogy a kvantumos interferenciajelenségek nagy távolságokon is felléphetnek, feltéve hogy az energia nem nagy. (Emlékezzünk a foton önmagával való interferenciájára és Clausen és Aspect EPR-kísérletére.) A jellegzetes kvantumgravitációs tömegskála a Planck-tömeg néven ismert
mP = 10–5 gramm
(közelítőleg). Ez látszólag sokkal nagyobb a kívántnál, minthogy jóval kisebb tömegű objektumok, például a porszemek klasszikus viselkedése közvetlenül észlelhető. (Az mP tömeg valamivel kisebb egy bolha tömegénél.) Nem hiszem azonban, hogy az egygravitonos feltétel ennyire durván érvényes. Megpróbálok egy kicsivel világosabb lenni, ám az írás idején még sok a homály és a kétség arra vonatkozóan, hogyan kell e feltételt pontosan alkalmazni. -írja.
2./
3./
Vissza kell térnünk az eredeti kérdésre. Hogyan kapcsolódik mindez ahhoz a fizikához, amely agyunk működését szabályozza? Mi köze lehet ennek gondolatainkhoz és érzéseinkhez?
9. Igazi agyak és modellagyak
Milyen is az agy?
Fejünkben van egy csodálatos szerkezet, amely irányítja cselekedeteinket, és valahogyan tudatossá teszi bennünk a környező világot. Mégis, ahogy Alan Turing egyszer megfogalmazta,165 leginkább egy tál hideg zabkására emlékeztet! Nehéz elképzelni, hogy egy megjelenésével ennyire keveset ígérő objektum hogyan képes azokra a csodákra, amelyekről tudomásunk van. A közelebbi vizsgálat azonban lassan felfedi, hogy szerkezete sokkal bonyolultabb, szervezettsége kifinomultabb (9.1. ábra). Felül a nagy, tekervényes (és leginkább kásaszerű) rész a nagyagy. Középen tisztán két részre oszlik, a bal és jobb féltekékre, elöl és hátul lényegesen kevésbé tisztán a homloklebenyre és három másikra: a fali, a halántéki és a nyakszirti lebenyre. Tovább lefelé, hátul található az agynak egy kisebb és inkább gömbszerű része – talán két gyapjúgombolyagra emlékeztet –, a kisagy. Mélyen belül, a nagyagy alatt egy sor furcsa, bonyolultnak látszó szerkezet bújik meg: a híd és a nyúltvelő (benne a retikuláris formáció, ez a tartomány később érdekes lesz számunkra), amelyek az agytörzs alsó részét alkotják, a talamusz, a hipotalamusz, a hippocampus, a kérgestest és sok egyéb különös nevű képződmény.
Az a rész, amelyre az emberi lényeknek, úgy érzik, a legbüszkébbeknek kell lenniük, a nagyagy – nem csak azért, mert az emberi agy legnagyobb része, hanem mert az embernél arányaiban is nagyobb, mint az állatoknál. (Az ember kisagya is nagyobb, mint a legtöbb állaté.) A nagyagynak és a kisagynak viszonylag vékony külső szürkeállomány rétege és nagyobb belső fehérállomány rétege van. E szürkeállományok a nagyagykéreg és kisagykéreg nevet viselik. A szürkeállomány az, ahol a különféle számítási feladatok végrehajtása történik, míg a fehérállomány hosszú idegszálakat tartalmaz, amelyek jeleket visznek az agy egyik részéből a másikba.
A nagyagykéreg különböző részei nagyon speciális feladatokat látnak el. A látókéreg a nyakszirti lebeny egyik tartománya az agy hátsó részén, itt történik a látás érzékelése és értelmezése. Különös, hogy a Természet ezt a tartományt választotta a szemből érkező jelek értelmezésére, noha a szem, legalábbis az embernél, a fej elülső részén helyezkedik el! Ám a Természet ennél még furcsábbat is alkotott. A nagyagy jobb féltekéje majdnem kizárólag a test bal oldalával, bal féltekéje pedig a test jobb oldalával foglalkozik, tehát gyakorlatilag minden idegnek át kell térnie egyik oldalról a másikra, amikor belép a nagyagyba, vagy elhagyja azt! A látókéreg jobb oldala nem a bal szemmel, hanem mindkét szem bal oldali látómezejével kapcsolódik, a bal oldali látókéreg hasonlóképpen mindkét szem jobb oldali látómezejével. Ez azt jelenti, hogy mindkét szem ideghártyájának jobb oldali idegei a jobb oldali, bal oldali idegei a bal oldali látókéreghez kell fussanak (emlékezzünk rá, hogy az ideghártyán a kép fordított állású). (Lásd 9.2. ábra.) Ily módon a bal oldali látómező egy nagyon jól meghatározott leképezése jön létre a jobb oldali látókéregben, és fordítva.
A fültől érkező jelek szintén áttérnek az agy ellentétes oldalára ezen a furcsa módon. A jobb hallókéreg (a jobb halántéki lebeny része) főként a balról észlelt hangokkal foglalkozik, a bal hallókéreg a jobbról észleltekkel. A szaglás kivétel az általános szabályok alól. A nagyagy elülső részén (a frontális lebenyben) elhelyezkedő jobb szaglókéreg főként a jobb orrüreggel, a bal a bal orrüreggel foglalkozik.
A tapintás érzékelése a fali lebeny egyik tartományában az ún. szomatoszenzoros (testérzékelő) kéregben történik. Ez a tartomány közvetlenül a homloklebeny és fali lebeny határfelülete mögött helyezkedik el. Nagyon jellegzetes a megfeleltetés a testfelület különböző részei és a szomatoszenzoros kéreg tartományai között. Ezt olykor grafikusan szemléltetik a „szomatoszenzoros emberkével”, amely egy, a szomatoszenzoros kéreg mentén elfekvő, torzított emberalak (lásd 9.3. ábra). A jobb szomatoszenzoros kéreg a test bal oldaláról jövő érzetekkel foglalkozik, a bal a jobb oldalról jövőkkel. Van a homloklebenynek egy megfelelő tartománya, amely éppen a homloklebeny és fali lebeny határfelülete előtt található, az ún. motoros (mozgató) kéreg. Ez a test különböző részei mozgásának aktiválásával foglalkozik, és itt is megtalálható a nagyon jellegzetes megfeleltetés a test különféle izmai és a motoros kéreg tartományai között. E megfeleltetést a 9.4. ábra „motoros emberkéje” ábrázolja. A jobb motoros kéreg a test bal oldalát, a bal a jobb oldalt irányítja.
A nagyagykéreg most felsorolt (látó-, halló-, szagló-, szomatoszenzoros és motoros) tartományait elsődlegeseknek nevezik, mert ezek kapcsolódnak a legközvetlenebbül az agy bemeneteihez és kimeneteihez. Ezen elsődleges tartományok közelében vannak a nagyagykéreg másodlagos tartományai, amelyek az absztrakció egy finomabb és bonyolultabb szintjét valósítják meg (lásd 9.5. ábra). Az érzékelés információi, amelyek a látó, halló és szomatoszenzoros kérgekbe érkeznek, a kapcsolt másodlagos tartományokban kerülnek feldolgozásra, a másodlagos motoros tartomány a kigondolt mozgástervekkel foglalkozik, amelyeket az elsődleges motoros kéreg fordít le tényleges izommozgásra a különböző meghatározott irányokban. (Megfontolásainkból hagyjuk ki a szaglókérget, mert az másképpen viselkedik, és meglehetősen keveset tudunk róla.) A nagyagykéreg maradék tartományait harmadlagosaknak (vagy asszociációs kéregnek) hívják. Az agy legelvontabb és leginkább kifinomult működése főként e területeken megy végbe. A sok különböző érzékelő tartomány információit az agy – összhangban, bizonyos mértékig, a külső részekkel – itt kapcsolja össze, nagyon összetett módon elemzi, emlékeket raktároz, képeket készít a külvilágról, általános terveket állít fel és értékel, megérti vagy kialakítja a beszédet.
A beszéd különösen érdekes, mert általában azt gondolják, hogy ez az emberi intelligenciának nagyon jellegzetes képessége. Furcsa, hogy a beszédközpontok (legalábbis a jobbkezes emberek hatalmas többségénél és a legtöbb balkezesnél is) főleg az agy bal oldalán találhatók. A lényeges területek a Broca-mező a homloklebeny alsó, hátsó részén és a Wernicke-mező a halántéklebeny felső, hátsó részén (lásd 9.6. ábra). A Broca-mező a mondatok kialakításával, a Wernicke-mező a nyelv értelmezésével foglalkozik. A Broca-mező sérülése elrontja a beszédet, de a megértést nem bántja, míg a Wernicke-mező sérülése esetén a beszéd folyamatos, de tartalma kevés. A két mezőt egy idegköteg, az ívelt fasciculus kapcsolja össze. Ha ez megsérül, akkor a megértés nem romlik, a beszéd folyamatos marad, de a megértés nem fejezhető ki szóban.
Most már kialakíthatunk egy nagyon durva képet arról, mit csinál a nagyagy. Az agy bemenete látható, hallható, tapintható és más jelekből áll össze, amelyeket először a nagyagyban (főként) a hátsó (fali, halántéki és nyakszirti) lebenyek elsődleges részei jegyeznek fel. Az agy kimenetét a test mozgásai aktiválásának formájában főként a nagyagy homloklebenyének elsődleges részei állítják elő. A kettő között feldolgozási folyamat megy végbe. Általában az agyműködés szerepváltással, funkcióátadással írható le, amely a hátsó lebenyek elsődleges részeitől indul, áthúzódik a másodlagos részekre, ahol a bemeneti adatok elemzése folyik, majd a hátsó lebenyek harmadlagos részeire, ahol az adatok teljes megértése történik (például a beszéd megértése a Wernicke-mezőn). Ezt a feldolgozott információt az ívelt fasciculus – az előbb említett idegköteg, most már az agy mindkét oldalán – elszállítja a homloklebenyhez, amelynek harmadlagos tartományaiban általános cselekvési tervek készülnek (például a beszéd kialakítása a Broca-mezőn). Ezeket a másodlagos motoros területek a testmozgások specifikusabb fogalmaivá alakítják, végül az agyműködés átterjed az elsődleges motoros kéregre, amely a test különféle izomcsoportjai felé (gyakran egyszerre többhöz) küld jeleket.
Egy szuperszámítógép képe rajzolódik ki előttünk. Az EMI hívei (vö. 1. fejezet) azt tartanák, hogy az egész az algoritmikus számítógép egy legmagasabb szintű példája – valójában egy Turing-gép –, ahol van egy bemenet (mint a Turing-gép bemeneti szalagja a bal oldalon) és egy kimenet (mint a gép kimeneti szalagja a jobb oldalon), és mindenfajta bonyolult számítás a kettő között megy végbe. Az agy természetesen függetlenül, meghatározott érzékelő bemenetek nélkül is képes működni. Ez akkor következik be, amikor valaki gondolkodik, számol vagy eltűnődik a múlt emlékein. Az EMI hívei számára ezek az agyműködések egyszerűen további algoritmikus tevékenységet jelentenek, és szerintük a „tudatosság” jelensége akkor lép fel, amikor az ilyen belső aktivitás eléri a kifinomultság megfelelő szintjét.
Nem szabad azonban túlságosan sietnünk a kész magyarázatokkal. A nagyagy működésének előbb vázolt általános képe csak nagyon durva kép. Még a látás érzékelése sem annyira egyszerű, ahogy azt elmondtam. A kéregnek van néhány egyéb (bár parányibb) tartománya, ahová a látómező, nyilvánvalóan különféle más célokból, leképeződik. (Látásunk tudatossága valószínűleg nem ide tartozik.) Vannak egyéb kiegészítő szenzoros és motoros tartományok is a nagyagykéregben szétszórva (a szem mozgásait például a hátsó lebenyek egyes pontjaiban lehet aktiválni).
Leírásomban még nem is említettem a nagyagyon kívüli részek szerepét. Mi a szerepe például a kisagynak? Láthatóan a test pontos koordinálásáért és vezérléséért felelős – a mozgás időzítéséért, egyensúlyáért és finomságáért. Képzeljük magunk elé egy táncos áradó művészetét, egy hivatásos teniszjátékos könnyed pontosságát, egy autóversenyző villámgyors vezetését, egy festő vagy zenész kezének biztos mozgását; gondoljunk egy gazella kecses ugrásaira vagy egy lopakodó macskára. A kisagy nélkül az ilyen pontosság nem volna lehetséges, és minden mozgás sutává és otrombává válna. Úgy látszik, hogy amikor valaki megtanul egy új mozgást, legyen az séta vagy autóvezetés, kezdetben minden mozdulatát részletesen végig kell gondolnia, és így a nagyagy ellenőrzése alatt áll; de mikor már jól elsajátította azt – és „második énjévé” vált –, akkor a kisagy veszi át a szabályozást. Mi több: mindennapos tapasztalat, hogy ha egy mozgásban, amelyet már begyakorolt, valaki gondol arra, amit csinál, akkor a könnyed szabályozás átmenetileg elveszhet. A rágondolás, úgy látszik, a nagyagyi ellenőrzés felélesztésével jár, a folyamatos és pontos kisagyi működés elvész. Kétségtelen, hogy az ilyen leírások túlságosan is leegyszerűsítettek, mégis jól összefoglalják a kisagy szerepét.166
A nagyagy működésének korábbi leírásában az is félrevezető volt, hogy az agy egyéb részeit figyelmen kívül hagytam. A hippocampus például létfontosságú szerepet játszik a hosszú távú (állandó) memória felépítésében, a tényleges emlékek valahol a nagyagykéregben tárolódnak – valószínűleg sok helyen egyszerre. Az agy rövid távon más módokon is meg tud őrizni képeket; percekig, sőt órákig képes azokat megtartani (talán az „emlékezetben”). Ám hogy vissza tudjon idézni ilyen képeket, miután figyelme már elterelődött róluk, ahhoz valahol állandósítva le kell rakni azokat, és ebben lényeges a hippocampus szerepe. (Sérülése félelmetes helyzetet teremt: az egyén nem képes új emlékek megőrzésére, miután figyelme már elterelődött azokról.) A kérgestest az a tartomány, amely révén a jobb és bal nagyagyi félteke érintkezik egymással. (Eltávolításának néhány meglepő következményét később majd látni fogjuk.) A hipotalamusz az érzelmek – öröm, düh, félelem, kétségbeesés, éhség – székhelye, közvetíti mind szellemi, mind fizikai megnyilvánulásaikat. A jelek folyamatosan áramlanak a hipotalamusz és a nagyagy különböző részei között. A talamusz fontos feldolgozó központ és közvetítőállomás, sok idegi bemenetet továbbít a külvilágból a nagyagykéreghez. A retikuláris formáció az agy egészének vagy különböző részeinek általános készültségi és tudatossági állapotáért felelős. Számos idegpálya kapcsolja össze ezeket, és sok más, létfontosságú területet.
A fenti leírás csak áttekintés az agy legfontosabb részeiről. E szakaszt azzal fejezem be, hogy valamivel többet mondok az agy szervezéséről mint egészről. Különböző részeit három tartományba lehet besorolni, amelyek a gerincoszloptól távolodva sorban az utóagy (vagy rhombencephalon), a középagy (vagy mesencephalon) és az előagy (vagy prosencephalon). A korai embrionális állapotban e három tartomány, ebben a sorrendben, három hólyag a gerincoszlop végénél. A legutolsó, a fejlődő előagy a két oldalon két hólyagszerű dudort növeszt, ezekből lesznek a nagyagyi féltekék. A teljesen kifejlődött előagy az agy sok fontos részét foglalja magában – nemcsak a nagyagyat, hanem a kérgestestet, a talamuszt, a hipotalamuszt, a hippocampust és sok más részt is. A kisagy az utóagy része. A retikuláris formáció egyik része a középagyban, a másik az utóagyban van. Törzsfejlődési értelemben az előagy a „legújabb”, az utóagy a „legrégibb”.
Remélem, e rövid vázlat, noha sok tekintetben elégtelen, ad valami elképzelést az Olvasónak arról, milyen is az emberi agy, és hogy általában mit csinál. Mindeddig alig érintettem a tudatosság központi kérdését. Foglalkozzunk a következőkben ezzel.
165 Egy BBC rádióadásban; lásd Hodges (1983), 7. fejezet.
166 A nagyagy „keresztező” viselkedése a kisagynál érdekes módon nincs meg, a kisagy jobb fele nagyjából a
Hol van a tudatosság székhelye?
Sok különböző nézet látott napvilágot az agy állapotának és a tudatosság jelenségének kapcsolatát illetően. Figyelemre méltóan kevéssé egyeznek a vélemények egy ilyen nyilvánvalóan fontos kérdésben. Világos azonban, hogy a tudatosság megnyilvánulásában az agynak nem minden területe vesz egyformán részt. Például, amint az előbbiekben utaltam rá, a kisagy sokkal inkább látszik „automatának”, mint a nagyagy. A kisagyi szabályozás alatti cselekvések majdnem „önmaguktól” mennek végbe, anélkül, hogy „gondolni” kellene rájuk. Míg valaki tudatosan elhatározhatja, hogy elsétál egyik helyről a másikra, az ellenőrzött mozgáshoz szükséges részletes izommozgások alaposan kidolgozott terve nagyon gyakran nem válik tudatossá. Ugyanez mondható a nem tudatos, reflexszerű cselekvésekről, amikor például visszarántjuk kezünket a forró kályhától, amit lehet, hogy nem is az agy közvetít, hanem a gerincoszlop felső része. Ebből legalábbis jó okunk lehet arra következtetni, hogy a tudatosság jelenségének valószínűleg több köze van a nagyagy tevékenységéhez, mint a kisagyéhoz vagy a gerincagyéhoz.
Másrészt egyáltalán nem világos, hogy a nagyagy tevékenységének önmagában mindig be kell-e avatkoznia tudatosságunkba. Például, ahogy az előbbiekben leírtam, a séta rendes tevékenységében, amikor nem vagyunk tudatában izmaink és végtagjaink részletes működésének – lévén ennek szabályozása nagyrészt kisagyi (segítenek benne az agy és a gerincagy más részei) –, a nagyagy elsődleges motoros tartományai, úgy látszik, szintén részt vesznek. Mi több, ugyanez igaz az elsődleges szenzoros tartományokra: lehet, hogy séta közben nem vagyunk tudatában a talpunkra gyakorolt változó nyomásnak, ám a szomatoszenzoros kéreg megfelelő tartományai folyamatosan aktiválódnak.
Wilder Penfield, a neves kanadai idegsebész (aki az 1940-es és 50-es években kiemelkedő tevékenységet végzett az emberi agy motoros és szenzoros tartományainak részletes feltérképezésében) azt bizonygatta, hogy tudatosságunk nem kapcsolódik pusztán a nagyagyi tevékenységhez. Tudatos alanyokon elvégzett számos agyműtét tapasztalatai alapján azt állította, hogy az általa felső agytörzsnek nevezett területet, amely nagyjából a talamuszt és a középagyat tartalmazza (vö. Penfield és Jasper 1947) – bár ő főként a retikuláris formációra gondolt –, kell valamilyen értelemben a „tudatosság székhelyének” tekinteni. A felső agytörzs összeköttetésben áll a nagyaggyal, és Penfield azt állította, hogy „tudatos felismerés” vagy „tudatosan elhatározott cselekvés” akkor jön létre, amikor az agytörzs e tartománya közvetlen összeköttetésben áll a nagyagykéreg megfelelő tartományával, nevezetesen az érzetekkel, gondolatokkal, emlékekkel társított speciális területtel, vagy cselekvéseket érzékelünk vagy idézünk elő tudatosan. Rámutatott arra, hogy noha képes ingerelni például az alany motoros agykérgének azon tartományát, amely a jobb kar mozgását okozza (és a jobb kar valóban mozog), ez nem idézi elő azt, hogy az alany akarja mozgatni jobb karját. (Valóban az alany még ki is nyújthatja bal karját és megállíthatja jobb karjának mozgását – mint Peter Sellers ismert filmszerepében, a Dr. Strangelove-ban!) Penfield azt sugallta, hogy a mozgás kívánsága sokkal inkább kötődhet a talamuszhoz, mint a nagyagykéreghez. Nézete szerint a tudatosság a felső agytörzs aktivitásának megnyilatkozása, de minthogy még valamire szükség van, aminek tudatában vagyunk, ezért nemcsak az agytörzs keveredik bele az ügybe, hanem a nagyagykéreg valamelyik tartománya is, amelyik abban a pillanatban összeköttetésben áll a felső agytörzzsel, és amelynek aktivitása megjeleníti e tudatosság szubjektumát (érzet, benyomás vagy emlék) vagy objektumát (szándékos cselekvés).
Más idegélettan-kutatók is állították, hogy különösen a retikuláris formáció tekinthető a tudatosság „székhelyének”, ha valóban létezik ilyen székhely. A retikuláris formáció mindenekelőtt az agy általános készültségi állapotáért felelős (Moruzzi és Magoun 1949). Sérülésének eszméletlenség a következménye. Amikor az agy éber, tudatos állapotban van, akkor a retikuláris formáció aktív; ellenkező esetben nem. Valóban: világos kapcsolat látszik a retikuláris formáció aktivitása és az egyén állapota között, amelyet rendesen „tudatosnak” nevezünk. A dolgot azonban bonyolítja az a tény, hogy az álom állapotában, amikor az egyén valóban „tudatos” abban az értelemben, hogy az álomnak magának tudatában van, a retikuláris formáció rendesen aktív részei nem látszanak aktívnak. Egy másik dolog, amely szintén visszatartja az embereket attól, hogy a retikuláris formációnak ilyen megtisztelő rangot tulajdonítsanak, az, hogy a fejlődést tekintve nagyon régi része az agynak. Ha a tudatossághoz csupán egy aktív retikuláris formációra van szükség, akkor a békák, gyíkok, sőt a tőkehalak is tudatosak!
Én ezt az utolsó érvet nem tekintem nagyon erősnek. Mi bizonyítékunk van arra, hogy a gyíkok és tőkehalak nem rendelkeznek valamilyen alacsony szintű tudatossággal? Milyen jogon állítjuk, mint egyesek teszik, hogy bolygónkon egyedül az emberi lények vannak megáldva a képességgel, hogy „tudatában” legyenek valaminek? A földi teremtmények között mi vagyunk-e az egyetlenek, akik „lenni” lehetünk képesek? Kétlem. Noha a békák és gyíkok és különösen a tőkehalak nem nagyon erősítik bennem a meggyőződést, hogy szükségszerűen „van ott valaki”, aki visszabámul rám, amikor nézem őket, benyomásom egy „lélek jelenlétéről” nagyon erős, amikor egy kutyát vagy macskát látok, vagy különösen akkor, amikor egy emberszabású majom néz engem az állatkertben. Nem állítom, hogy úgy éreznek, mint én, még azt sem, hogy sok finomság van abban, amit éreznek. Nem hiszem, hogy „öntudatosak” bármiféle erős értelemben (noha úgy sejtem, hogy az öntudatosság eleme jelen lehet167). Mindössze azt állítom, hogy olykor egyszerűen éreznek! Elfogadnám, hogy – mint az álom állapotában – a tudatosság valamilyen formája jelen van, de feltehetően egészen alacsony szinten. Ha a retikuláris formáció egyes részei valamilyen módon kizárólagosan felelősek a tudatosságért, akkor az álom állapotában ezeknek, bár alacsony szinten, de aktívaknak kellene lenniük.
Egy másik nézőpont szerint (O’Keefe 1985) a hippocampus működése az, aminek több köze van a tudatos állapothoz. Mint korábban megjegyeztem, a hippocampus döntő fontosságú a hosszú távú emlékek raktározásában. Fel lehet vetni, hogy az állandó memória létrehozása összekapcsolódik a tudattal, és ha ez igaz, akkor a hippocampus valóban központi szerepet játszik a tudatosság jelenségében.
Mások azt tartják, hogy a nagyagykéreg maga felelős a tudatosságért. Minthogy a nagyagy az ember büszkesége (bár a delfineké ugyanolyan nagy!), és minthogy az intelligenciával legszorosabb kapcsolatban álló szellemi tevékenységet a nagyagy végzi, ezért az ember lelke biztosan itt lakozik! Feltehetően ez volna például az EMI nézőpont következtetése. Ha a „tudatosság” csupán egy algoritmus összetettségével – vagy esetleg „mélységével” vagy valamilyen „bonyolultsági fokkal” – összefüggő tulajdonság, akkor, az EMI szemlélet szerint, a nagyagykéreg által elvégzett bonyolult algoritmusok volnának a legerősebb bizonyítékai annak, hogy ez a tartomány képes a tudat megvalósítására.
Sok filozófus és pszichológus hangoztatja azt a nézetét, hogy az emberi tudat nagyon szorosan kötődik az emberi nyelvhez. Eszerint csupán nyelvbéli képességeink folytán jutunk a kifinomult gondolkodáshoz, amely emberi voltunk igazi jele – magának a lelkünknek a kifejezése. E nézet szerint a nyelv az, ami megkülönböztet az állatoktól, és mentséget nyújt arra, hogy megfosztjuk őket szabadságuktól, és leöljük őket, amikor szükségét érezzük. A nyelv engedi meg, hogy filozofáljunk, hogy leírjuk, mit érzünk, hogy meggyőzhessünk másokat arról, hogy mi tudatában vagyunk a külső világnak és saját magunknak is. E szemlélet a nyelvet tekinti tudatosságunk kulcsának.
Vissza kell most idéznünk, hogy a nyelv központjai (az emberek hatalmas többségénél) az agynak éppen a bal oldalán vannak (Broca- és Wernicke-mezők). A most elmondott nézőpont tehát magával vonná azt, hogy a tudatosság csupán a bal oldali nagyagykéreghez kötődik, a jobb oldalihoz nem! Valóban ez a véleménye számos idegélettan-kutatónak [különösen John Eccles (1973) hangoztatja ezt], bár nekem mint kívülállónak, e nézet nagyon furcsának tetszik. Az okokat el fogom magyarázni.
167 Meggyőző bizonyítékok szólnak amellett, hogy legalábbis a csimpánzok képesek az öntudatosságra, ezt mutatják azok a kísérletek, amelyekben megengedték, hogy tükrökkel játsszanak (vö. Oakley 1985, 4. és 5. fejezet).
Agyhasításos kísérletek
Sok megfigyelést végeztek olyan emberi lényeken (és állatokon), akiknek kérgestestét teljesen átvágták, ezért a nagyagykéreg bal és jobb féltekéje nem volt képes kommunikálni egymással. Az embereknél168 a kérgestest átvágása műtéti gyógykezelésként történt, úgy találták, hogy ezzel hatásosan tudják kezelni az epilepszia különösen súlyos formáját, amelyben ezek az emberek szenvedtek. Roger Sperry és munkatársai számos pszichológiai tesztet végeztek velük műtétük után bizonyos idővel. Úgy helyezték el őket, hogy bal és jobb látómezejüket teljesen független ingerek érjék, így a bal félteke csak a jobb oldalról, a jobb félteke csak a bal oldalról kapott vizuális információt. Ha egy ceruzát villantottak fel a jobb oldalon, és egy csészét a balon, akkor a személy azt mondta, „Ez egy ceruza”, mert az agy beszédre képes oldala a ceruzát érzékelte. Azonban a bal kéz képes volt kiválasztani egy csészealjat egy darab papírral szemben, mint ami a csészével összekapcsolható. A bal kéz a jobb félteke ellenőrzése alatt áll, és ez a félteke, bár beszédre képtelen, el tud végezni bizonyos egészen összetett és jellegzetesen emberi műveleteket. Azt állították például, hogy rendes körülmények között a geometriai gondolkodás (különösen három dimenzióban) és a zene is főleg a jobb félteke dolga, ezzel ellensúlyozza a bal szóbeli és elemző képességeit. A jobb agy képes megérteni közneveket vagy elemi mondatokat, és végre tud hajtani nagyon egyszerű aritmetikai feladatokat.
E hasított agyú alanyoknál az a legmeglepőbb, hogy a két oldal gyakorlatilag független egyénként látszik viselkedni, a kísérletező mindkettővel külön-külön kommunikálhat – noha ez a jobb féltekével nehezebb és primitívebb szintű, mint a ballal, mert az előbbinél hiányzik a beszéd képessége. Az alany nagyagyának egyik fele egyszerű módon kommunikálhat a másikkal, például figyelve a másik oldal által vezérelt kar mozgását, vagy esetleg árulkodó hangokat (egy csészealj csörömpölését) hallgatva. Ám gondosan ellenőrzött laboratóriumi feltételek mellett még ez a primitív kommunikáció is megszüntethető a két oldal között. Homályos érzelmi kapcsolat azonban még mindig maradhat, feltehetően azért, mert a ketté nem vágott szerkezetek, mint például a hipotalamusz, még összeköttetésben állnak mindkét oldallal.
Kínálkozik a kérdés: két különálló tudatos egyén lakozik-e testünkben? Ez a kérdés sok vita tárgya volt. Egyesek szerint a válasz biztosan „igen”, mások azt állítják, hogy egyik oldal sem tekinthető önmagában egyénnek. Vannak, akik így érvelnek: az a tény, hogy az érzelmek a két oldal számára közösek lehetnek, bizonyítéka annak, hogy mégiscsak egyetlen egyénről van szó. Egy másik nézőpont szerint csak a bal félteke képvisel tudatos egyént, a jobb csak automata. Ezt, úgy látszik, olyanok gondolják, akik a nyelvet a tudatosság lényeges összetevőjének tartják. Valóban csak a bal félteke képes meggyőzően „Igen!” választ adni a szóbeli kérdésre: „Tudatos Ön?” A jobb félteke, mint egy kutya, macska vagy csimpánz, még kibetűzni is nagyon nehezen képes a kérdést alkotó szavakat, és képtelen a választ megfelelően szavakba önteni.
A kérdést mégsem lehet ily könnyen elintézni. Egy komoly érdeklődést kiváltó újabb kísérletben Donald Wilson és munkatársai (Wilson és mások 1977; Gazzaniga, LeDoux és Wilson 1977) egy „P. S.” nevű, kettéhasított agyú alanyt vizsgáltak. A műtét után csak a bal félteke tudott beszélni, de mindkettő megértette a beszédet; később a jobb félteke is megtanult beszélni! Nyilvánvalóan mindkét félteke tudatos volt. Mi több, külön-külön látszottak tudatosnak, mert különböző örömeik és vágyaik voltak. Például a bal félteke leírta, hogy műszaki rajzoló szeretne lenni, a jobb pedig azt, hogy autóversenyző!
Magam egyszerűen nem tudom elhinni azt a gyakori állítást, hogy a közönséges emberi nyelv szükséges a gondolkodáshoz vagy a tudatossághoz. (A következő fejezetben majd ismertetem okaimat.) Ezért azok pártját fogom, akik általánosságban úgy vélik, hogy a kettéhasított agyú alany két fele egymástól függetlenül lehet tudatos. P. S. példája erősen alátámasztja, hogy legalábbis ebben a speciális esetben valóban mindkét fél az lehet. Véleményem szerint P. S. és a többiek között ebben a vonatkozásban az egyetlen igazi különbség az, hogy az ő jobb oldali tudata ténylegesen is meg tud győzni másokat a létezéséről!
Ha elfogadjuk, hogy P. S.-nek valóban két független értelme van, akkor figyelemre méltó helyzet áll elő. A műtét előtt feltételezhetően minden hasított agyú alany csak egyetlen tudattal rendelkezett; utána azonban kettővel! Valamilyen módon az eredeti egyetlen tudat vált ketté. Felidézhetjük az 1. fejezet hipotetikus utazóját, aki alávetette magát a távfuvarozó masinának, és aki (szándékán kívül) annak ébredt tudatára, hogy állítólagos „tényleges” énje megérkezett a Vénuszra. Az ő tudatának kettéválása látszólag paradoxonhoz vezet. Megkérdezhetjük ugyanis, hogy tudatának árama „ténylegesen” milyen utat követett: „Ha Ön volt az utazó, akkor melyikük végül is az »Ön«?” A távfuvarozó masina elintézhető azzal, hogy sci-fi, ám P. S. esetében látszólag analóg helyzettel van dolgunk, de ez valóban megtörtént! P. S. melyik tudatossága „azonos” a műtét előtti P. S.-sel? Sok filozófus bizonyára elutasítaná a kérdést mint értelmetlent. Nem látszik ugyanis mód az eldöntésére. Az operáció előtt a két félteke osztozott egy tudatos létezés emlékeiben, és nem kétséges, hogy mindkettő állíthatná, hogy ő az igazi. Ez figyelemre méltó lehet, de önmagában nem paradoxon. Mindazonáltal van valami határozottan rejtélyszerű az egészben.
A rejtély még tovább fokozódna, ha a két tudatot később megint össze lehetne valahogy hozni. A kérgestest átvágott idegeinek újraegyesítése a jelenlegi technika mellett nem jön számításba, ám el lehet képzelni valami enyhébb dolgot, mint az idegrostok tényleges átvágását. Esetleg be lehetne időlegesen fagyasztani ezeket az idegeket, vagy valamilyen szerrel megbénítani. Nincs tudomásom arról, hogy végrehajtottak volna ilyen kísérletet, de feltételezem, hogy technikailag hamarosan kivihetővé válik. A kérgestest újraaktiválása után feltételezhetően megint csak egy tudatosság létezne. Képzelje el, hogy ez éppen Ön! Milyen érzés volna, hogy valamikor a múltban két különálló ember volt, külön „énekkel”?
168 Az első ilyen jellegű kísérleteket macskákon végezték (vö. Myers és Sperry 1953). Az agyhasítási kísérletekről további információra lásd Sperry (1966), Gazzaniga (1970), MacKay (1987).
Vaklátás
Az agyhasításos kísérletek legalábbis jelzik, hogy nem lehet egyetlen „tudatosságszékhely”. Vannak azonban más kísérletek, amelyek azt látszanak alátámasztani, hogy a nagyagykéreg egyes részei jobban összekapcsolhatók a tudatossággal, mint mások. Az egyik ilyen a vaklátás jelenségével függ össze. A látókéreg egy tartományának sérülése vakságot okozhat a megfelelő látómezőben. A látómező e tartományában lévő tárgyat az alany nem észleli, mert erre a tartományra vonatkozóan vak.
Egyes furcsa felfedezések (vö. Weiskrantz 1987) azonban arra utalnak, hogy a dolgok nem ennyire egyszerűek. Egy D. B. nevű beteg látókérge egy részét el kellett távolítani, ennek az lett a következménye, hogy látómezejének egy bizonyos tartományában semmit sem látott. Ám ha valamit erre a területre helyeztek, és megkérdezték D. B.-t, mit sejt, mi az a valami (rendszerint egy kereszt vagy kör alakú jel, vagy valamilyen szögben megdöntött vonaldarab), akkor közel 100% pontossággal helyes választ adott! E „sejtések” pontossága magát D. B.-t is meglepte, de megerősítette, hogy abban a tartományban semmit sem képes érzékelni.169
Az ideghártyától kapott képeket az agy bizonyos, a látókéregtől különböző tartományokban is feldolgozza, az ilyen rejtettebb tartományok egyike az alsóbb, halántéki lebenyben fekszik. Valószínű, hogy D. B. „sejtéseit” ezen alsóbb halántéki tartományból szerzett információra alapozhatta. E területek aktiválása által semmit nem észlelt közvetlenül, tudatosan, az információ mégis ott volt, és D. B. „sejtéseinek” helyességében lepleződött le. Némi gyakorlás után D. B. korlátozott mértékű valódi tudatosságot fejlesztett ki e tartományokra vonatkozóan.
Mindez azt látszik mutatni, hogy a nagyagykéreg egyes területei (például a látókéreg) jobban kapcsolódnak a tudatos érzékeléshez, mint mások, de azt is, hogy gyakorlással e más területek közül bizonyosak láthatóan kapcsolatba hozhatók a közvetlen tudatossággal.
169 A vaklátást némileg kiegészíti a „vakság tagadása” néven ismert helyzet, amelyben egy személy, aki ténylegesen teljesen vak, ragaszkodik ahhoz, hogy egészen jól lát, úgy látszik, vizuálisan tudatosul benne a kikövetkeztetett környezet! (Lásd Churchland 1984, 143. o.)
Információfeldolgozás a látókéregben
Az agy részei közül a legjobban a látókéregnél értjük azt, hogyan kezeli a kapott információt; működésének magyarázatára változatos modelleket készítettek.170 A vizuális információ feldolgozásának egy része még az ideghártyában megtörténik, mielőtt az elérné a látókérget. (Az ideghártyát valójában az agy részének kell tekintenünk!) Az első kísérletek egyike, amely útmutatást adott arra vonatkozóan, hogyan megy végbe a feldolgozás a látókéregben, az volt, amelyért David Hubel és Torsten Wiesel 1981-ben elnyerték a Nobel-díjat. Kísérleteikben meg tudták mutatni, hogy egy macska látókérgében bizonyos sejtek a látómező azon vonalaira fogékonyak, amelyek meghatározott szögben dőlnek. Más, közeli sejtek a más meredekségű vonalakat dolgozzák fel. Nem nagyon számított, mi az, ami ilyen szögben áll. Lehetett az a sötét és világos terület határvonala, vagy egy sötét vonal világos háttérben. A vizsgált speciális sejtek ezt az egyetlen tulajdonságot, „a meredekség szögét” dolgozták fel. Megint más sejtek meghatározott színekre vagy a jobb és a bal szem által észleltek közötti különbségekre fogékonyak, így válik lehetővé a mélységbeli érzékelés. Az elsődleges befogadó tartományoktól távolodva olyan sejteket találunk, amelyek látásérzékelésünk egyre finomabb részleteire érzékenyek. Amikor például ránézünk a 9.7. ábra rajzára, egy teljes fehér háromszöget érzékelünk; pedig a háromszöget alkotó vonalak nincsenek teljesen rajta az ábrán, csak következtetünk rájuk. A (másodlagosnak nevezett) látókéregben ténylegesen találtak sejteket, amelyek képesek feljegyezni e kikövetkeztetett vonalak helyzetét!
A 70-es évek elején megjelentek az irodalomban olyan állítások,171 hogy egy majom látókérgében felfedeztek egy sejtet, amely csak akkor válaszolt, amikor egy arc képe jelent meg az ideghártyán. Ennek alapján fogalmazták meg a „nagymamasejt-hipotézist”, amely szerint vannak az agyban bizonyos sejtek, amelyek csak akkor válaszolnak, amikor az alany nagyanyja belép a szobába! Valóban vannak újabb felfedezések, amelyek arra utalnak, hogy bizonyos sejtek csak speciális szavakra fogékonyak. Ez talán valamilyen módon a nagymamasejt-hipotézis igazolása felé vezet?
Nyilvánvaló, hogy az agyműködés részleteit illetően rengeteg tanulnivalónk van még. Nagyon kevéssé tudjuk, hogyan tesznek eleget feladataiknak a magasabb agyközpontok. Tegyük most félre ezt a kérdést, és fordítsuk figyelmünket az agy sejtjeire, amelyek képessé teszik ezekre a figyelemre méltó mutatványokra.
170 A látókéreg működésének olvasmányos leírására lásd Hubel (1988), 419. o..
171 Lásd Hubel (1988), 221. o. Korábbi kísérletek olyan sejteket derítettek fel, amelyek csak egy kéz képére érzékenyek.
1./
Az agy részei közül a legjobban a látókéregnél értjük azt, hogyan kezeli a kapott információt; működésének magyarázatára változatos modelleket készítettek.170 A vizuális információ feldolgozásának egy része még az ideghártyában megtörténik, mielőtt az elérné a látókérget. (Az ideghártyát valójában az agy részének kell tekintenünk!)
...
(Az ideghártyát valójában az agy részének kell tekintenünk!)
"Az ideghártya, másnéven retina a pupillán keresztül a szembe érkező fényt továbbítja az agyba, biztosítva a látást. Amennyiben az ideghártyát sérülés éri, a látás módosulhat.
olvasom az Internetről, mert – szégyen – az előzőekben olvasottakból nem volt egyértelmű számomra, hogy hol is van az ideghártya, azt hittem mindenfajta idegi érzékelésnek van egy hártyája…
Hogy elfelejtettem…amit olyan régen tanultam, hiszen a hallásnál az ideghártya szerepét, vagyis az ingerület átadást a szőrsejtek biztosítják, amelyek a rezgést elektromos jelekké alakítják.
"A belső fülben található a csigajárat és azok a rendkívül érzékeny szőrszálak, melyek minden rezgésre megremegnek. A szőrsejtek a rezgést elektromos jelekké alakítják, melyek majd az agyba jutnak, ami végül hangként (pl. beszédként, zajként, stb.) értelmezi azokat."
"Öt érzék ezer muzsikája" - a címe kedvenc könyveim egyikének. Bármilyen csábítónak tűnik is itt és most elmerülni az Interneten fellelhető - és onnan le is tölthető - vonatkozó tudományos és ismeretterjesztő könyvekben, ezt most nem lehet, mert akkor a történet - és ez az írásom is - végtelenné válna.
...Mert ott van például a Pszichológia tudománya, ami hajdanán (többek között a katonai időm 11 hónapja alatt is) annyira érdekelt.
...
Emlékek itt belül. Hogyan lehetne lejutni hozzájuk, felszínre hozni őket? van rá módszer? És itt van a kérdésemre rögtön egy elkeserítő válasz Pléh Csaba: Pszichológia c. könyvéből:
...
Hogyan működnek az idegi jelek?
Az agy (valamint a gerincoszlop és az ideghártya) által végzett minden feldolgozási műveletet a test figyelemreméltóan sokoldalú idegsejtjei, az ún. neuronok teszik lehetővé.172 Próbáljuk megnézni, milyen is egy neuron. A 9.8. ábrán ennek rajza látható. Van egy központi, némileg csillagszerű, gyakran inkább retekhez hasonlító gumó, a sejttest, amely a sejtmagot tartalmazza. Ennek egyik végéből egy hosszú idegszál nyúlik ki – olykor valóban nagyon hosszú ahhoz képest, hogy egyetlen mikroszkopikus sejtnek tekintjük és nevezzük (az emberben gyakran néhány centiméteres is lehet) –, ez az axon. Az axon egy „huzal”, amely a sejt kimeneti jelét továbbítja. Az axon sokszor kettéválik, sok kisebb ág sarjadzhat ki belőle. Az így létrejövő idegszálak végein egy kis csomó, a végfácska található. A sejttest másik végén, gyakran mindenféle irányban szétágazva láthatók a faszerű dendritek, ezek szállítják a bemeneti adatokat a sejttesthez. (Esetenként végfácskák is vannak a dendriteken, ezek létesítik az ún. dendrodendritikus szinapszisokat a dendritek között. Tárgyalásomban ezeket figyelmen kívül hagyom, minthogy az általuk okozott bonyodalom lényegtelen.)
Az egész sejtet, sejttestet, axont, végfácskákat, dendriteket, lévén önálló egység, sejthártya veszi körül. Hogy a jelek az egyik neurontól a másikhoz eljussanak, valahogyan „át kell ugraniuk” a közöttük lévő „gáton”. Ez a szinapszis néven ismert kapcsolatban történik, amelyben az egyik neuron végfácskája egy másik neuron egy pontjához kötődik vagy a sejttesten, vagy az egyik dendriten (lásd 9.9. ábra). A végfácska és a sejttest vagy dendrit között, amelyhez előbbi kapcsolódik, nagyon szűk rés van, ennek neve szinaptikus szakadék (lásd 9.10. ábra). A neuronok közötti jelnek át kell jutnia ezen a résen.
Milyen formát öltenek az idegszálak mentén terjedő, a szinaptikus szakadékokon átjutó jelek? Mi készteti a következő neuront, hogy jelet bocsásson ki? Az olyan kívülálló számára, mint magam is vagyok, a Természet által választott eljárások rendkívülinek – és teljesen elbűvölőnek látszanak! Azt gondolhatnánk, hogy a jelek a drótban haladó elektromos áramhoz hasonlíthatnának, de a helyzet ennél sokkal bonyolultabb.
Egy idegszál lényegében egy hengeres cső, amely közönséges konyhasó (nátrium-klorid) és kálium-klorid oldatainak elegyét tartalmazza, főleg az utóbbit, így a csőben nátrium-, kálium- és kloridionok vannak (9.11. ábra). Ezek az ionok kívül is megtalálhatók, de más arányokban, kívül több a nátriumion, mint a kálium. Az ideg nyugalmi állapotában a csőben negatív eredő elektromos töltés van (azaz több a kloridion, mint a nátrium- és káliumion együttesen – emlékezzünk arra, hogy a nátrium- és káliumion pozitív, a kloridion negatív töltésű), a csövön kívül pozitív (azaz több a nátrium- és kálium-, mint a kloridion). A sejthártya, amely a henger felületét képezi, valamennyire „lyukas”, ezért az ionok igyekeznek átszivárogni rajta és eltüntetni a töltéskülönbséget. Ezt ellensúlyozza, és a negatív töltés túlsúlyát belül fenntartja egy „metabolikus pumpa”, amely a hártyán keresztül lassan visszanyomja a nátriumionokat. Ez részben arra is szolgál, hogy fenntartsa belül a kálium túlsúlyát a nátriummal szemben. Van egy másik (valamivel kisebb méretű) metabolikus pumpa, amely káliumionokat nyom be kívülről, ezzel járul hozzá a káliumionok belső túlsúlyához (noha a töltésegyensúly ellen dolgozik).
A szál mentén terjedő jel létrehoz egy olyan tartományt, amelyben a töltéstúlsúly ellentétes (azaz belül pozitív, kívül negatív), ez a tartomány is mozog (9.12. ábra). Képzeljük azt, hogy ott ülünk az idegroston az ilyen fordított töltésű tartomány előtt. Amint közeledik, elektromos mezeje kis „ajtókat”, ún. nátriumkapukat nyit a sejthártyán; ezeken a nátriumionok kívülről visszafolyhatnak a belső részbe (az elektromos mező és a sűrűségkülönbségek következtében kialakult nyomás, az ún. „ozmózis” hatására). Ennek eredményeképpen a töltés belül lesz pozitív, kívül pedig negatív. Amikor ez megtörténik, akkor a töltésfordított tartomány, amely a jelet képezi, elérkezik hozzánk. Ekkor újabb kis „ajtók” (káliumkapuk) nyílnak, amelyeken a káliumionok folyhatnak vissza belülről, és megkezdődik a negatív töltések belső túlsúlyának helyreállítása. A jel továbbhaladt! Végül, amikor a jel már elhagyta a vizsgált szakaszt, akkor a pumpák lassú, de könyörtelen működése visszanyomja a nátriumionokat kívülre, a káliumionokat belülre. Az idegszál nyugalmi állapota visszaáll, kész fogadni a következő jelet.
Hangsúlyoznunk kell, hogy a jel egyszerűen egy, a szál mentén terjedő töltésfordított tartomány. Az anyag maga (az ionok) nagyon kevéssé mozog – csak ki és be a sejthártyán keresztül!
Ez a furcsa, egzotikus mechanizmus nagyon hatásosan működik. Alkalmazása egyetemleges, gerinceseknél és gerincteleneknél egyaránt megtalálható. A gerincesek azonban egy további újítást hajtottak végre, náluk az idegrostot szigetelő réteg veszi körül fehér, zsíros anyagból, ez az ún. myelin. (A myelinréteg adja a színét az agy „fehér anyagának”) E szigetelés teszi lehetővé, hogy az idegjelek (a „közvetítőállomások” között) gyengülés nélkül és igen tekintélyes – egészen 120 méter per másodpercig terjedő – sebességgel mozogjanak.
Amikor a jel egy végfácskához érkezik, akkor az kémiai anyagot, ún. neurotranszmittert bocsát ki magából. Ez az anyag a szinaptikus szakadékon keresztül átjut egy másik neuronhoz – vagy egyik dendritjének, vagy magának a sejttestnek egyik pontjához. Na már most, egyes, neuronok végfácskái olyan neurotranszmitter vegyületet bocsátanak ki, amely „tüzelésre” serkenti a következő neuron sejttestét, azaz arra, hogy új jelet indítson el axonja mentén. Ezek a serkentő szinapszisok. Mások gátolják a következő neuron tüzelését, ezek a gátló szinapszisok. Az adott pillanatban aktív serkentő szinapszisok hatásai összeadódnak, az ugyancsak aktív gátlóak hatásai ebből levonódnak, és ha az eredő elér egy bizonyos kritikus küszöbértéket, akkor a következő neuron valóban tüzelni fog. (A serkentő szinapszisok pozitív elektromos potenciálkülönbséget hoznak létre a következő neuron belseje és külseje között, a gátlóak negatívat. Ezek a potenciálkülönbségek adódnak össze. A neuron akkor fog tüzelni, amikor e potenciálkülönbség a csatlakozó axonon kritikus szintet ér el, amikor a kálium nem képes elég gyorsan helyreállítani az egyensúlyt.)
172 A ma már jól megalapozott elméletet, mely szerint az idegrendszer különálló sejtekből, a neuronokból áll, 1900 körül a nagy spanyol neuroanatómus, Ramón y Cajal vetette fel nyomatékosan.
Számítógépes modellek
Az idegi átvitel egyik fontos tulajdonsága, hogy a jelek (nagy többségükben) teljesen „minden-vagy-semmi” jelenségek. A jel erőssége nem változik: vagy van jel, vagy nincs. Ez az idegrendszer működésének egy digitális számítógépéhez hasonló jelleget ad. Valójában igen sok hasonlóság van a nagyszámú összekapcsolt neuron tevékenysége és egy digitális számítógép belső működése között, főleg ha az utóbbi áramvezető drótjaira és logikai kapuira gondolunk (ezekről mindjárt többet mondok). Elvileg nem nehéz elkészíteni egy ilyen adott neuronrendszer számítógépes szimulációját. Természetesen vetődik fel a kérdés: nem jelenti-e ez azt, hogy bármilyen is az agy részletes huzalozása, az mindig modellezhető egy számítógéppel?
Hogy az összehasonlítás világosabb legyen, meg kell mondanom, mi is igazában egy logikai kapu. A számítógépben szintén „minden-vagy-semmi” helyzet áll elő, egy huzalon keresztül vagy érkezik áramlökés, vagy nem; erőssége, ha van, mindig ugyanakkora. Minthogy minden nagyon pontosan van időzítve, egy ilyen pulzus hiánya is határozott jel, amit a számítógép „észrevesz”. Valójában amikor a „logikai kapu” kifejezést használjuk, hallgatólagosan egy pulzus jelenlétére vagy hiányára gondolunk, amelynek rendre „igaz” vagy „hamis” jelentése van. Ennek semmi köze nincs a tényleges igazsághoz vagy hamissághoz; csupán az általánosan használt terminológiáról van szó. Rendeljük hozzá az „1” számjegyet az „igaz” jelhez (van jel), a „0” számjegyet a „hamis” jelhez (nincs jel), és mint a 4. fejezetben tettük, használjuk az „∧” jelet az „és” jelölésére (amely az az „állítás”, hogy mindkettő „igaz”, azaz a válasz akkor és csak akkor 1, ha mindkét eredmény 1), a „∨” jelet a „vagy” jelölésére (ami azt „jelenti”, hogy egyik vagy másik, vagy mindkettő „igaz”, azaz a válasz akkor és csak akkor 0, ha mindkét eredmény 0), a „⇒” jelet az „implikálja” jelölésére (azaz A ⇒ B azt jelenti, hogy „ha A igaz, akkor B igaz”, ami ekvivalens azzal, hogy „vagy A hamis, vagy B igaz”), a „” jelet az „akkor és csak akkor” jelölésére (mindkettő „igaz” vagy mindkettő „hamis”) és a „~” jelet a „nem” jelölésére („igaz”, ha „hamis”; „hamis”, ha „igaz”). E változatos logikai műveletek hatásait az ún. „igazságtáblák” segítségével lehet kifejezni:
ahol minden esetben A címkézi a sorokat (azaz A = 0 adja az első, A = 1 a második sort), B az oszlopokat. Ha például A = 0 és B = 1, ami mindegyik tábla jobb felső elemét adja, akkor A ⇒ B értékére a harmadik táblából 1-et kapunk. (Szóbeli példa a tényleges logikai kifejezésekkel: a „ha alszom, akkor boldog vagyok” állítás triviálisan teljesül abban a speciális esetben, ha ébren vagyok és boldog.) Végül a „nem” logikai kapu hatása egyszerűen:
~0 = 1 | és | ~1 = 0. |
Ezek a logikai kapuk alaptípusai. Van néhány egyéb is, de azok mind felépíthetők a felsoroltakból.173
Fel tudunk-e most építeni egy számítógépet neuronos kapcsolatokból? Meg fogom mutatni, hogy ez még a neurontüzelésnek az előbbiekben tárgyalt nagyon primitív formájával is lehetséges. Nézzük meg, hogyan lehet elvileg logikai kapukat építeni neuronkapcsolatokból. A számjegyek valamilyen új kódolási formájára van szükségünk, mert egy jel hiánya nem vezérel semmit. Válasszuk (teljesen önkényesen) a dupla pulzust az 1 (vagy „igaz”), a szimpla pulzust a 0 (vagy „hamis”) jelölésére, és vegyük azt az egyszerűsített rendszert, amelyben egy neuron tüzelési küszöbét mindig két egyidejű serkentő pulzus jelenti. Könnyű megépíteni egy „és” (azaz „∧”) kaput. Amint azt a 9.13. ábra mutatja, legyen a két bemeneti idegrost az egyetlen végfácska pár a kimeneti neuronon. (Ha mindkettő dupla pulzust ad, akkor az első és második pulzus egyaránt eléri a megkövetelt kétpulzusos küszöböt, míg ha valamelyik csak egyszeres pulzust szolgáltat, akkor csak az egyik pár éri azt el. Feltételezem, hogy a pulzusok időzítése nagyon pontos, és hogy a határozottság kedvéért a dupla pulzus esetén az első pár határozza meg az ütemet.) A „nem” kapu (azaz „~”) felépítése lényegesen bonyolultabb, egy lehetséges módja a 9.14. ábrán látható. A bemeneti jel itt egy axon mentén érkezik, amely két ágra oszlik. Az egyik kerülő utat tesz meg, éppen olyan hosszúságút, hogy a jelet pontosan egy dupla pulzus két pulzusa között eltelt idővel késleltesse, utána mindkét ág még egyszer kettéválik, az egyik ág mindkettőnél egy gátló neuronon végződik, de a késleltetett ág először még kettéhasad, és ezek egyike közvetlenül, a másik ismét késleltetve jut a gátló neuronra. Ennek a neuronnak a kimenete semmi, ha a bemenet egyszeres pulzus, és egy (késleltetett) dupla pulzus, ha a bemenet dupla pulzus. Az ezt a kimenetet szállító axon három ágra válik szét, mindhárom gátló végfácskákban végződik a végső serkentő neuronon. Az eredeti megosztott axon megmaradó két része megint kettéválik, és mind a négy ág a végső neuronon végződik most serkentő szinapszisokban. Az Olvasó ellenőrizheti, hogy e végső serkentő neuron a megkövetelt „nem” kimenetet szolgáltatja (azaz dupla pulzust, ha a bemenet egyszeres pulzus és egyszereset, ha a bemenet dupla). (Ez a séma abszurd módon bonyolultnak látszik, de jobbat nem ismerek!) Az Olvasó elszórakozhat még azzal, hogy a többi, előbb felsorolt logikai kapu közvetlen „neurális” konstrukcióját is megalkotja.
E konkrét példákat természetesen nem kell komoly modellnek tekinteni arra nézve, hogy mit csinál ténylegesen az agy. Csupán jelezni próbálom, hogy lényegében megvan a logikai ekvivalencia a neurontüzelés most megadott modellje és az elektronikus számítógép felépítése között. Könnyen látható, hogy egy számítógép a neuronkapcsolatok tetszőleges ilyen modelljét képes szimulálni; míg az előbb megadott részletes felépítések jelzik azt a tényt, hogy fordítva, a neuronrendszerek képesek egy számítógépet szimulálni – és ezért képesek úgy működni, mint egy (univerzális) Turing-gép. Noha a Turing-gépek tárgyalásánál a 2. fejezetben logikai kapukról nem volt szó,174 és noha ezeknél sokkal többre van szükségünk, ha egy általános Turing-gépet akarunk szimulálni, új elvi kérdés nem merül fel – feltéve, hogy egy Turing-gép végtelen szalagját egy nagy, de véges neuronbankkal közelíthetjük. Ez látszólag azt bizonyítja, hogy az agy és a számítógép lényegében egyenértékű!
Ám mielőtt túl gyorsan elfogadnánk e következtetést, meg kell vizsgálnunk az agy és a jelenlegi számítógépek működése közötti sokféle különbséget, amelyek lényegesek lehetnek. Leírásomban először is némiképp túlegyszerűsítettem a neuron tüzelését mint egy minden-vagy-semmi jelenséget. Ez az axon mentén haladó egyetlen pulzusra vonatkozott, ám amikor egy neuron ténylegesen „tüzel”, akkor gyors egymásutánban egész sor ilyen pulzust bocsát ki. A neuron még akkor is bocsát ki pulzusokat, amikor nem aktiválódik, csak ekkor lassúakat. Amikor tüzel, akkor az egymást követő pulzusok frekvenciája nő meg igen nagy mértékben. A neurontüzelésnek van valószínűségi oldala is. Ugyanaz az inger nem mindig hozza létre ugyanazt az eredményt. Továbbmenve: az agyműködésnek nincs meg az az egészen pontos üteme, amelyre az elektronikus számítógépeknél szükség van; és rá kell mutatnunk arra is, hogy a neuronok működése – másodpercenként maximálisan 1000 körüli sebességükkel – nagyon sokszor, kb. 10–6-szor lassúbb, mint a leggyorsabb elektronikus áramköröké. Az elektronikus számítógép nagyon pontos hálózatával szemben a neuronok tényleges kapcsolódásaiban nagyon sok a véletlenszerűség és az átfedés – bár ma már tudjuk, hogy az agy „huzalozása” (születéskor) sokkal-sokkal pontosabb, mint úgy ötven évvel ezelőtt gondolták.
A most elsoroltak legtöbbje az agy hátránya a számítógéppel való összehasonlításban. Vannak azonban más, az agy előnyére szolgáló tényezők is. A logikai kapuknak csak nagyon kevés (legfeljebb három vagy négy) be- és kimeneti huzaljuk van, míg a neuronok igen nagyszámú szinapszissal rendelkezhetnek. (Szélsőséges példaként a kisagy Purkinje-sejtek néven ismert neuronjain kb. 80 000 serkentő szinaptikus végződés található.) Az agy neuronjainak teljes száma is felülmúlja még a legnagyobb számítógép tranzisztorjainak számát is – e szám valószínűen 1011 az agynál, és „csak” 109 körüli a számítógépnél! Ez utóbbi azonban a jövőben várhatóan növekedni fog.175 Továbbmenve: az agysejtek nagy számát főként a kisagyban található temérdek kis szemcsesejt teszi ki – ezek száma harmincmilliárd (3 · 1010) körül van. Ha elhisszük, hogy egyszerűen a neuronok számának nagysága az, ami megengedi, hogy tudatos tapasztalataink legyenek, míg a jelenlegi számítógépeknek, úgy tetszik, nincsenek, akkor további magyarázatot kell találnunk arra, miért látszik a kisagy tevékenysége tökéletesen tudattalannak, miért társítható a tudatosság a nagyaggyal, noha csak kb. kétszer több (kb 7 · 1010) neuronja van, sokkal kisebb sűrűségben.
173 Valójában minden logikai kapu felépíthető csak a „~” és „∧” kapukból (sőt egyedül a ~(A∧B) műveletből is).
174 A logikai kapuk használata közelebb áll egy elektronikus számítógép felépítéséhez, mint a 2. fejezet részletes Turing-gép meggondolásai. Abban a fejezetben elméleti okokból volt a hangsúly Turing megközelítésén. A számítógép fejlesztés ugyanannyit nyert a kiváló magyar-amerikai matematikus, Neumann János munkásságából, mint Alan Turingéból.
175 Ezek az összehasonlítások sok tekintetben félrevezetőek. A mai számítógépek tranzisztorainak hatalmas többsége nem a logikai műveletekkel, hanem a „memóriával” kapcsolatos, és a memória kívülről mindig, lényegében tetszés szerinti mértékben, tovább bővíthető. A párhuzamos műveletek növekedésével több tranzisztor kerülhet közvetlen kapcsolatba a logikai műveletekkel, mint jelenleg.
Az agy alakíthatósága
Vannak egyéb eltérések is az agy és a számítógép működése között, amelyek szerintem sokkal fontosabbak, mint az eddig felsoroltak; ezek az agy alakíthatósága néven ismert jelenséggel függnek össze. Valójában az agyat nem tekinthetjük egyszerűen egy felhuzalozott neuronokból összerakott, állandó gyűjteménynek. A neuronok közötti kapcsolatok nem rögzítettek, mint lennének a fenti számítógépmodellben, hanem állandóan változnak. Nem azt mondom, hogy az axonok vagy dendritek helyzetei változnak. A bonyolult „huzalozás” nagy része lényegében a születésnél már kialakult. A szinaptikus kapcsolatokra gondolok, ahol a tényleges érintkezés zajlik a különböző neuronok között. Ezek gyakran a dendrittüskéken jönnek létre, amelyek a dendritek pici kidudorodásai, ide csatlakozhatnak a végfácskák (lásd 9.15. ábra). A „csatlakozás” nem jelent érintkezést, hanem az éppen megfelelő távolságú – nagyjából egy negyvenezred milliméternyi – szűk rést (szinaptikus szakadék). Ezek a dendrittüskék bizonyos körülmények között összezsugorodhatnak, a kapcsolat megszűnhet, vagy megnőhetnek (újak is nőhetnek), és új kapcsolatokat létesíthetnek. Ezért ha úgy gondolunk az agy neuronjainak kapcsolataira, mint amelyek lényegében egy számítógépet alkotnak, akkor ez olyan számítógép, amely állandóan változni képes!
A hosszú távú emlékezet raktározásának egyik élenjáró elmélete szerint a szinaptikus kapcsolatoknak ez a változása szolgáltatja a szükséges információ tárolásának módját. Ha ez így van, akkor láthatjuk, hogy az agy alakíthatósága nem csupán véletlen bonyodalom, hanem az agyműködés lényeges sajátossága. Milyen mechanizmus képezi e folyamatos változások alapját? Milyen gyorsak lehetnek a változások? A második kérdésre a válasz vitatott, de legalábbis az egyik iskola szerint az ilyen változások másodpercek alatt bekövetkezhetnek. Ezt várnánk akkor, ha az ilyen változások volnának felelősök az állandó memória tárolásáért, minthogy annak elraktározása valóban másodpercek dolga lehet (vö. Kandel 1976). Ennek lényeges következményei lehetnek számunkra, vissza fogok rá térni a következő fejezetben.
Mi a helyzet az agy alakíthatóságának mechanizmusaival? Egy (Donald Hebbtől származó, 1954) ötletes elmélet javaslata szerint léteznek bizonyos, a következő tulajdonsággal bíró szinapszisok (a „Hebb-szinapszisok”): az A és B neuron közötti Hebb-szinapszis erősödik, ha A tüzelését követi B tüzelése, gyengül, ha nem követi. Ez független attól, hogy a Hebb-szinapszis maga lényegesen közrejátszik-e B tüzelésében. Így a „tanulás” valamilyen formája jön létre. Változatos matematikai modelleket állítottak fel, amelyekkel ennek az elméletnek az alapján megpróbálták utánozni a tanulás/feladatmegoldás tevékenységet. Ezek az ún. ideghálózatok. Úgy látszik, az ilyen modellek valóban képesek valamiféle kezdetleges tanulásra, ám egyelőre messze vannak attól, hogy valószerű agymodellek legyenek. Mindenesetre valószínűnek látszik, hogy a szinaptikus kapcsolatok változásait szabályozó mechanizmusok sokkal bonyolultabbak a megemlítetteknél. Világos, hogy jobban meg kellene értsük ezeket.
Van egy másik, ezzel összefüggő vonatkozása a végfácskák neurotranszmitter felszabadításának. Olykor ez egyáltalán nem a szinaptikus szakadékokban történik meg, hanem belép az általános sejtközi folyadék, esetleg más, távoli neuronokat befolyásolva. Sokféle különböző neurokémiai anyag szabadulhat fel ezen a módon – és léteznek az emlékezésnek az elmondottól eltérő elméletei, amelyek az ilyen előfordulható vegyületek különböző lehetséges változataira alapoznak. Az agy állapotát bizonyára befolyásolhatja általában e vegyületek jelenléte, amelyek az agy más részeiben keletkeznek (például a hormonok). A neurokémia egész kérdése bonyolult, és nehéz átlátni, hogyan készíthetnénk egy megbízható, részletes számítógépes szimulációt mindarról, ami lényeges lehet ezen a területen.
Párhuzamos számítógépek és a tudatosság „egyetlen” volta
Sok ember van azon a véleményen, hogy a párhuzamos számítógépek fejlesztése jelenti az emberi agy képességeivel rendelkező gép megépítésének kulcsát. Tekintsük át nagy vonalakban ezt a jelenleg oly népszerű elképzelést. Egy párhuzamos számítógép, a sorossal ellentétben, nagyon nagyszámú, önálló számítást végez el a többitől függetlenül, és e nagyrészt autonóm műveletek eredményeit csak időnként kombinálja össze, hogy végrehajtsa az együttes számítási feladatot. A számítógépek ilyen felépítési típusát főként az a szándék motiválta, hogy utánozzák az idegrendszer működését, minthogy az agy különböző részei valóban elkülönült és egymástól független számítási feladatokat látszanak végrehajtani (ilyen például a vizuális információ feldolgozása a látókéregben).
Két dolgot kell tisztáznunk. Az első az, hogy elvileg nincs különbség egy párhuzamos és egy soros számítógép között. Tulajdonképpen mindkettő Turing-gép (vö. 2. fejezet). Különbségek csak a számítás hatásfokában vagy sebességében lehetnek. Vannak olyan típusú számítások, amelyeknél a párhuzamos szervezés valóban hatékonyabb, de semmi esetre sem mondhatjuk, hogy mindig ez a helyzet. A második pont az, hogy – legalábbis véleményem szerint – nagyon valószínűtlen, hogy a párhuzamos, klasszikus számítástechnika volna a kulcsa annak, ami tudatos gondolkodásunk során végbemegy. A tudatos gondolkodás egyik jellegzetes tulajdonsága (legalábbis amikor az egyén normális pszichológiai állapotban van, és nem alanya egy „agyhasításos” operációnak!) az „egyetlensége” – szemben nagyon sok egyidejűleg végbemenő független cselekvéssel.
A „Hogyan várhatják tőlem, hogy egyszerre több dologra gondoljak?” kijelentések mindennaposak. Lehetséges-e egyáltalán különböző dolgokat egyidejűleg tudatunkban tartani? Talán lehet néhány dolgot egyszerre, de ez inkább hasonlít a különböző témák közötti állandó előre-hátra repkedéshez, mintsem ahhoz, hogy egyidejűleg, tudatosan és egymástól függetlenül gondolnánk rájuk. Ha tudatosan két dologra gondolnánk egészen függetlenül egymástól, akkor ez inkább olyan volna, mintha csak időlegesen is, de két különálló tudatunk volna. A tapasztalat azonban azt mutatja, hogy (legalábbis normális embernél) egyetlen tudat létezik, amely homályosan több dologról tudhat, de amelyik tetszőleges időpontban csak egyetlen speciális dologra koncentrál.
Hogy mit értünk „egy dolog” alatt, az persze egyáltalán nem világos. A következő fejezetben találkozunk az „egyetlen gondolat” néhány nagyon figyelemreméltó példájával Poincaré és Mozart ihletésében. Ám nem kell ilyen messzire mennünk, hogy felismerjük: amiről egy személy bármelyik pillanatban tudomással bírhat, az nagyon bonyolult lehet. Képzeljük például el azt, amikor eldöntjük, mit fogunk vacsorázni. Egyetlen ilyen tudatos gondolat nagyon sok információt tartalmazhat, aminek teljes szóbeli kifejezése egészen hosszúra is nyúlhat.
Én úgy látom, hogy a tudatos felfogás eme „egyetlensége” teljesen ellenkezik a párhuzamos számítógép képével. Az a kép viszont sokkal megfelelőbb lehet az agy nem tudatos működésének modellezésére. Különféle független mozgások – séta, egy gomb begombolása, lélegzés vagy még a beszéd is – mind végrehajthatók egyidejűleg és többé-kevésbé önállóan, anélkül, hogy bármelyikre tudatosan gondolnánk!
Másrészt nekem úgy tetszik, hogy elképzelhető bizonyos kapcsolat a tudatosság eme „egyetlensége” és a kvantumos párhuzamosság között. Emlékezzünk rá, hogy a kvantumelmélet szerint a kvantumszinten különböző alternatívák élhetnek együtt lineáris szuperpozícióban! Így egyetlen kvantumállapot elvileg nagyszámú különböző tevékenységet tartalmazhat, amelyek mind egyidejűleg mennek végbe. Ezt értem kvantumos párhuzamosságon, és hamarosan megvizsgáljuk a „kvantumszámítógép” elméleti elképzelését, amelyben ez a kvantumos párhuzamosság elvileg felhasználható nagyszámú egyidejű számítás elvégzésére. Ha egy tudatos „szellemi állapot” valamiképp hasonló lehet egy kvantumállapothoz, akkor az „egyetlenség” vagy a globális gondolat valamely formája megfelelőbbnek bizonyulhat, mint a közönséges párhuzamos számítógép esetében. Vannak vonzó oldalai ennek az elképzelésnek, amelyekre a következő fejezetben vissza fogok térni. Ám mielőtt ezzel komolyan foglalkozhatnánk, fel kell tennünk a kérdést, lehet-e egyáltalán szerepük a kvantumos jelenségeknek az agy működésében.
...
1./– legalábbis véleményem szerint – nagyon valószínűtlen, hogy a párhuzamos, klasszikus számítástechnika volna a kulcsa annak, ami tudatos gondolkodásunk során végbemegy. A tudatos gondolkodás egyik jellegzetes tulajdonsága (legalábbis amikor az egyén normális pszichológiai állapotban van, és nem alanya egy „agyhasításos” operációnak!) az „egyetlensége” – szemben nagyon sok egyidejűleg végbemenő független cselekvéssel.
2./A „Hogyan várhatják tőlem, hogy egyszerre több dologra gondoljak?” kijelentések mindennaposak. Lehetséges-e egyáltalán különböző dolgokat egyidejűleg tudatunkban tartani? Talán lehet néhány dolgot egyszerre, de ez inkább hasonlít a különböző témák közötti állandó előre-hátra repkedéshez, mintsem ahhoz, hogy egyidejűleg, tudatosan és egymástól függetlenül gondolnánk rájuk. Ha tudatosan két dologra gondolnánk egészen függetlenül egymástól, akkor ez inkább olyan volna, mintha csak időlegesen is, de két különálló tudatunk volna. A tapasztalat azonban azt mutatja, hogy (legalábbis normális embernél) egyetlen tudat létezik, amely homályosan több dologról tudhat, de amelyik tetszőleges időpontban csak egyetlen speciális dologra koncentrál.
...…Úgyhogy lassabban annak a „Multitasking-üzemmódnak” a dicsőítésével (fülükön a fejhallgató: szól a zene, kezükben az „okostelefon” – hüvelykujjuk villámgyors mozgásával hozzák elő, vagy írják be az újabb is újabb információkat, miközben esetleg két szemükkel az asztali gép vagy a táblagép kijelzőjére tapadnak). Hagy ez elég időt a szűrésre, arra, hogy az egyén számára lényeges információk átkerüljenek a hosszútávú memóriába? Lassú – mondják kicsit lesajnálóan a „menedzserkalkulátorok”– a nem multitasking üzemmódú emberekre, majd kicsit enyhítik és árnyalják a képet: lassú, de alapos. A gyerekek persze mások, talán az ő agyuk rugalmassága a „multitasking”-módot jól tudja kezelni. Egy elég jó fantasztikus regény az „Indigó gyerekek”-ről szólt, a multitasking üzemmódú jövő embereiről, úgy emlékszem ez volt a címe is.
Van-e szerepe a kvantummechanikának az agyműködésben?
Az idegi tevékenység előbbi vizsgálata teljesen klasszikus volt, kivéve azt, hogy szükségszerűen foglalkozott olyan fizikai jelenségekkel, amelyek alapját részben kvantummechanikai okok képezik (például az egységnyi elektromos töltésű ionok, a nátrium- és káliumkapuk, a meghatározott kémiai potenciálok, amelyek eldöntik az idegi jelek be/ki kapcsoló jellegét, a neurotranszmitterek kémiája). Van-e egyéb világos szerepe valódi kvantummechanikai szabályozásnak valamely kulcsfontosságú helyen? Ez szükségszerűnek látszik, ha az előző fejezet végén elmondottaknak van valami igazi jelentőségük.
Ténylegesen van legalább egy világos hely, ahol a kvantumszintű működés fontos lehet az idegi tevékenységben, és ez az ideghártya. (Emlékezzünk vissza, hogy az ideghártya technikailag az agynak része!) Békákon végzett kísérletek azt mutatják, hogy alkalmas körülmények között a sötétséghez szokott ideghártyába ütköző egyetlen foton elegendő lehet egy makroszkopikus idegi jel kiváltásához (Baylor, Lamb és Yau 1979). Ugyanez az embernél is igaznak látszik (Hecht, Shlaer és Pirenne 1941), de ott egy további mechanizmus is jelen van, amely elnyomja az ilyen gyenge jeleket, hogy azok ne zavarják a felfogott képet túl nagy vizuális „zajjal”. Kb. hét foton együttes jelére van szükség ahhoz, hogy egy sötétséghez szokott ember ténylegesen tudatosítsa a jelet. Mindazonáltal úgy látszik, hogy az emberi ideghártyában vannak egyetlen fotonra érzékeny sejtek.
Minthogy vannak az emberi testben neuronok, amelyek önmagukban álló kvantumos eseményekkel vezérelhetők, nem ésszerűtlen azt kérdezni, találhatók-e ilyen típusú sejtek valahol az emberi agy fő részében? Amennyire tudom, erre nincs bizonyíték. A megvizsgált sejttípusok mind megkövetelik egy küszöb elérését, és nagyon nagy számú kvantumra van szükség, hogy a sejt tüzeljen. Lehet azonban azon töprengeni, hogy valahol az agy mélyén vannak egyetlen kvantumra érzékeny sejtek. Ha ez igaznak bizonyul, akkor a kvantummechanika jelentős szerephez jut az agyműködésben.
Még ez sem tűnik nagyon hasznosan kvantummechanikainak, minthogy a kvantum csupán egy jel kiváltásának egy módja. Nem kapunk jellegzetes kvantumos interferenciajelenségeket. Úgy látszik, hogy ebből legjobb esetben is csak a bizonytalanság származhat, fog-e egy neuron tüzelni, vagy sem; nehéz látni, hogyan jelenthet nagyobb hasznot számunkra.
Egyes kérdések azonban nem egészen ilyen egyszerűek. Térjünk vissza az ideghártyához. Tegyük fel, hogy egy foton érkezik be rá, amely előzőleg visszaverődött egy félig ezüstözött tükörről. A foton állapota egy komplex lineáris szuperpozícióval írható le, amelynek egyik tagja az ideghártya egy sejtjével ütköző foton, a másik viszont nem találkozik ideghártyasejttel, hanem mondjuk kimegy az ablakon keresztül az utcára (vö. 6.17. ábra). Amikor elérkezik az a pillanat, amelyiknél becsapódhatott az ideghártyára, és ameddig a kvantumelmélet lineáris U szabálya (azaz a Schrödinger-állapotvektor determinisztikus fejlődése, lásd 6. fejezet) fennáll, addig komplex lineáris szuperpozíciót fog alkotni az, hogy van idegi jel, és az, hogy nincs. Amikor ez bekerül az alany tudatába, akkor az csak a két alternatíva egyikét fogja fel, és a másik kvantumos eljárásnak, az R-nek kellett működésbe lépnie (állapotvektor-redukció, lásd 6. fejezet). (Amikor ezt mondom, figyelmen kívül hagyom a sokvilág-nézőpontot, lásd 6. fejezet, amelynek megvannak a maga problémái!) Az előző fejezet végén érintett gondolatmenet szerint meg kell kérdeznünk, vajon elegendő anyagot zavart-e meg a jel elhaladása, teljesül-e az egygraviton-feltétel. Noha igaz, hogy az ideghártya tekintélyes nagyítást vitt végbe, amikor a foton energiáját a tényleges jelben mozgó tömeggé alakította át – elérte esetleg a 1020-szorost is –, ez még mindig nagyon sokszor kisebb az mP Planck-tömegnél (kb. 108-szorosan). Egy idegi jel azonban észlelhető változást hoz létre a környező elektromos mezőben (egy toroidális mező mozog az idegszál mint tengely mentén). Ez a mező jelentősen megzavarhatja a környezetet, benne az egygraviton-feltétel könnyűszerrel teljesülhet. Ezért a felvázolt nézőpont szerint az R eljárás már azelőtt működésbe léphetett, mielőtt észleljük vagy nem észleljük a fény felvillanását. Tudatunkra az állapotvektor redukciójához eszerint nincs szükség!
1./
Mindazonáltal úgy látszik, hogy az emberi ideghártyában vannak egyetlen fotonra érzékeny sejtek.
Kvantumszámítógépek
Ha már azon spekulálunk, hogy az egyetlen kvantumra érzékeny neuronok fontos szerepet játszanak mélyen az agy belsejében, akkor megkérdezhetjük, milyen hatásaik lehetnek. Először felvázolom Deutsch kvantumszámítógép-koncepcióját (vö. még 4. fejezet), utána rátérek arra a kérdésre, lényeges lehet-e ez a mi szempontunkból.
Mint már az előbb jeleztem, az alapvető elképzelés az, hogy kihasználják a kvantumos párhuzamosságot, amely szerint két egészen különböző dolgot úgy kell tekinteni, mint amelyek kvantumos lineáris szuperpozícióban vesznek részt – mint a foton, amely egyidejűleg verődik vissza és halad át a félig ezüstözött tükrön, vagy esetleg egyidejűleg halad át két résen. A kvantumszámítógépnél ez a két szuperponált, különböző dolog két különböző számítás volna. A feltevés szerint bennünket nem az érdekel, hogy megkapjuk a választ mindkét számításból, hanem valami más, ami részleges információt szed ki a szuperponált párból. Végül, amikor mindkettő kész, akkor egy alkalmas „megfigyelést” tennénk a két számításon, így kapnánk a kívánt választ.176 Így eszközünk időt tud megtakarítani azzal, hogy a két számítást egyidejűleg végzi! Az ily módon való eljárásból eddig nem látszik jelentős nyereség, minthogy feltehetően sokkal közvetlenebb módon használhatnánk két különálló klasszikus számítógépet párhuzamosan (vagy egyetlen klasszikus párhuzamos gépet), mint a kvantumosat. Az igazi nyereség azonban akkor mutatkozhat, amikor nagyon nagyszámú párhuzamos számításra van szükség – esetleg meghatározatlanul nagyszámúra –, amelyeknek nem egyedi eredményei érdekelnek bennünket, hanem az összes eredmény valamilyen alkalmas kombinációja.
A részletekbe menve: a kvantumszámítógép felépítése a logikai kapuk kvantumos változatait tartalmazná, a kimenet a bemenetre alkalmazott „unitér művelet” eredménye volna – egy példa az U eljárás – és a számítógép teljes működése egy U eljárás végrehajtása volna elejétől a végéig, amíg egy végső „megfigyelési aktus” behozza R-et.
Deutsch elemzése szerint a kvantumszámítógépek nem használhatók nem algoritmikus műveletek végrehajtására (azaz egy Turing-gép erejét meghaladó dolgokra), de bizonyos nagyon mesterségesen kigondolt helyzetekben, bonyolultságelméleti értelemben (lásd 4. fejezet) nagyobb sebességet érhetnek el, mint egy szabványos Turing-gép. Ezen elemzések eredménye egy kis csalódást okozott, tekintettel arra, hogy mennyire mellbevágó elképzelésekről volt szó, de ne felejtsük, még a kezdet kezdetén vagyunk csupán.
Hogyan kapcsolódhat mindez a jelentős számú, egyetlen kvantumra érzékeny neuront tartalmazó agy működésével? Az analógiával az a fő probléma, hogy a kvantumos hatások nagyon gyorsan elvesznek a „zajban” – az agy túl „forró” objektum ahhoz, hogy jelentős ideig megőrizze a kvantumos koherenciát (azaz az U folyamatos működése által szépen leírt viselkedést). A saját kifejezéseimmel ez azt jelentené, hogy az egygravitonos feltétel folyamatosan teljesülne, így az R művelet állandóan megszakítaná az U-t.
A helyzet eddig nem látszik nagyon sokat ígérőnek, ha azt várjuk, hogy a kvantummechanikából kapunk valami hasznosat az agyra nézve. Talán végül is arra vagyunk ítélve, hogy számítógépek legyünk! Magam ezt nem hiszem. További vizsgálatokra van azonban szükség, hogy megtaláljuk a helyes utat.
176 Deutsch leírásában a kvantumelmélettel kapcsolatban szívesebben használja a „sokvilág”-nézőpontot. Fontos azonban megértenünk, hogy ez teljesen lényegtelen, a kvantumszámítógép fogalma egyformán alkalmazható, bármelyik nézőpontot is fogadjuk el a hagyományos kvantummechanikát illetően.
1./
Az igazi nyereség azonban akkor mutatkozhat, amikor nagyon nagyszámú párhuzamos számításra van szükség – esetleg meghatározatlanul nagyszámúra –, amelyeknek nem egyedi eredményei érdekelnek bennünket, hanem az összes eredmény valamilyen alkalmas kombinációja.
A részletekbe menve: a kvantumszámítógép felépítése a logikai kapuk kvantumos változatait tartalmazná, a kimenet a bemenetre alkalmazott „unitér művelet” eredménye volna – egy példa az U eljárás – és a számítógép teljes működése egy U eljárás végrehajtása volna elejétől a végéig, amíg egy végső „megfigyelési aktus” behozza R-et.
2./ Hogyan kapcsolódhat mindez a jelentős számú, egyetlen kvantumra érzékeny neuront tartalmazó agy működésével? Az analógiával az a fő probléma, hogy a kvantumos hatások nagyon gyorsan elvesznek a „zajban” – az agy túl „forró” objektum ahhoz, hogy jelentős ideig megőrizze a kvantumos koherenciát (azaz az U folyamatos működése által szépen leírt viselkedést). A saját kifejezéseimmel ez azt jelentené, hogy az egygravitonos feltétel folyamatosan teljesülne, így az R művelet állandóan megszakítaná az U-t.
A helyzet eddig nem látszik nagyon sokat ígérőnek, ha azt várjuk, hogy a kvantummechanikából kapunk valami hasznosat az agyra nézve. Talán végül is arra vagyunk ítélve, hogy számítógépek legyünk! Magam ezt nem hiszem. További vizsgálatokra van azonban szükség, hogy megtaláljuk a helyes utat. -írja és lelkesen tovább hív az úton.
Túl a kvantumelméleten?
Visszatérek egy olyan kérdéshez, amely a könyv nagy részén végigvonul. Alkalmas-e igazán az agy és az értelem leírására a világról alkotott képünk, amelyet a klasszikus és kvantumelmélet szabályai irányítanak olyan formában, ahogy e szabályokat jelenleg értjük? Agyunk bármilyen „közönséges” kvantumos leírása nyilvánvaló rejtélyt tartalmaz, minthogy a „megfigyelés” a hagyományos kvantumelmélet elfogadott értelmezésének lényeges alkotórésze. „Önmagát megfigyelőnek” tekintsük-e az agyat, amikor egy gondolat vagy érzékelés belép a tudatba? A hagyományos elmélet nem ad világos szabályt arra, hogyan kellene ezt a kvantummechanikának figyelembe vennie, és ezáltal a kvantummechanikát az agyra mint egészre alkalmazni. Egy feltételt szándékoztam megfogalmazni R beindulására (az „egygraviton-feltételt”), amely teljesen független a tudattól, és ha valami hasonló teljesen összefüggő elméletté volna fejleszthető, akkor lehetőség nyílna az agy egy sokkal világosabb kvantumos leírására, mint amilyenek ma léteznek.
Azt hiszem azonban, nem csak az agyműködés leírásánál merülnek fel ezek az alapvető problémák. Maguknak a digitális számítógépeknek a működése is a kvantumos jelenségeken alapszik – olyan jelenségeken, amelyek, véleményem szerint, nem mentesek a kvantumelméletben benne rejlő nehézségektől. Mi ez a „létfontosságú” kvantumos függés? Hogy megértsük a kvantummechanika szerepét a digitális számítástechnikában, először azt kell megkérdeznünk, hogyan akarhatjuk, hogy egy teljesen klasszikus objektum digitális számítógépként viselkedjen. Az 5. fejezetben megvizsgáltuk a Fredkin–Toffoli-féle klasszikus „biliárdgolyó-számítógépet”; de azt is megjegyeztük, hogy ez az elméleti „eszköz” bizonyos idealizációkon alapszik, amelyek félretolnak egy lényeges, a klasszikus rendszerekben benne rejlő instabilitási problémát. Ezt a problémát úgy írtuk le, mint szétszóródást a fázistérben az idő haladtával (5.14. ábra), amely majdnem elkerülhetetlenül vezet a klasszikus eszköz működési pontosságának állandó csökkenésére. Ami végül megállítja a pontosság ilyen elvesztését, az a kvantummechanika. A modern, elektronikus számítógépekben a diszkrét állapotok létezése (a 0-val és 1-gyel való kódolás lehetősége) szükséges ahhoz, hogy egyértelmű dologgá váljék, mikor van a számítógép az egyik vagy másik ilyen állapotban. Ez az igazi lényege a számítógép-működés „digitális” természetének. Ez a diszkrétség végső soron kvantummechanikai. (Emlékezzünk vissza az energiaállapotok, a színképfrekvenciák vagy a spin stb. kvantumos diszkrét voltára, vö. 6. fejezet). Még a régi mechanikus számolómasinák is azon alapultak, hogy különféle részeik szilárdak – a szilárdság szintén a kvantumelmélet diszkrétségének következménye.177
A kvantumos diszkrétség azonban nem kapható meg csupán U működéséből. Ha valami, akkor a Schrödinger-egyenlet még rosszabb a nemkívánatos szétszóródás és „pontosságvesztés” megakadályozásában, mint a klasszikus fizika egyenletei! U szerint egyetlen részecske térben kezdetben lokalizált hullámfüggvénye az idő haladtával egyre nagyobb és nagyobb tartományokra terjed szét (6. fejezet). A bonyolultabb rendszerek olykor szintén a lokalizáció ilyen ésszerűtlen hiányától szenvednének (emlékezzünk Schrödinger macskájára!), ha R időről időre nem lépne közbe. (Egy atom diszkrét állapotaiban például az energia, az impulzus és a teljes impulzusmomentum határozott. Egy általános állapot, amely „szétszóródik”, az ilyen diszkrét állapotok szuperpozíciója. R időnkénti hatása az, ami előírja, hogy az atom ténylegesen e diszkrét állapotok egyikében „legyen”.)
Én úgy látom, hogy sem a klasszikus, sem a kvantummechanika – az utóbbi valamilyen alapvető változtatás nélkül, amely R-et „tényleges” folyamattá tenné – soha nem képes megmagyarázni azt, hogyan gondolkodunk. Talán még a számítógépek digitális működéséhez is az U és R közötti összjáték mélyebb megértése szükséges. A számítógépeknél legalább azt tudjuk, hogy működésük (mert úgy terveztük!) algoritmikus, és nem próbáljuk rájuk erőltetni a fizikai törvényekben feltételezett nemalgoritmikus viselkedést. Ám a helyzet az aggyal és az értelemmel, állítom, egészen más. Egy nyilvánvaló példával meg lehet mutatni, hogy a (tudatos) gondolkodási folyamatoknak lényeges nemalgoritmikus összetevői is vannak. A következő fejezetben megpróbálom kifejteni okaimat, amiért hiszek az ilyen összetevőben, és eltöprengek azon, milyen figyelemre méltó fizikai hatások képezhetnek egyfajta, az agyműködést befolyásoló „tudatosságot”.
177 E megjegyzés nem érvényes, ha megengedjük, hogy a „klasszikus” alkotórészek teljes fogak, tengelyek stb. legyenek. Az alkotórészeket én közönséges (mondjuk pontszerű vagy gömbszerű) részecskéknek veszem.
1./
Alkalmas-e igazán az agy és az értelem leírására a világról alkotott képünk, amelyet a klasszikus és kvantumelmélet szabályai irányítanak olyan formában, ahogy e szabályokat jelenleg értjük? Agyunk bármilyen „közönséges” kvantumos leírása nyilvánvaló rejtélyt tartalmaz, minthogy a „megfigyelés” a hagyományos kvantumelmélet elfogadott értelmezésének lényeges alkotórésze. „Önmagát megfigyelőnek” tekintsük-e az agyat, amikor egy gondolat vagy érzékelés belép a tudatba? A hagyományos elmélet nem ad világos szabályt arra, hogyan kellene ezt a kvantummechanikának figyelembe vennie, és ezáltal a kvantummechanikát az agyra mint egészre alkalmazni. Egy feltételt szándékoztam megfogalmazni R beindulására (az „egygraviton-feltételt”), amely teljesen független a tudattól, és ha valami hasonló teljesen összefüggő elméletté volna fejleszthető, akkor lehetőség nyílna az agy egy sokkal világosabb kvantumos leírására, mint amilyenek ma léteznek.
2./
A kvantumos diszkrétség azonban nem kapható meg csupán U működéséből. Ha valami, akkor a Schrödinger-egyenlet még rosszabb a nemkívánatos szétszóródás és „pontosságvesztés” megakadályozásában, mint a klasszikus fizika egyenletei! U szerint egyetlen részecske térben kezdetben lokalizált hullámfüggvénye az idő haladtával egyre nagyobb és nagyobb tartományokra terjed szét (6. fejezet). A bonyolultabb rendszerek olykor szintén a lokalizáció ilyen ésszerűtlen hiányától szenvednének (emlékezzünk Schrödinger macskájára!), ha R időről időre nem lépne közbe.
3./
Én úgy látom, hogy sem a klasszikus, sem a kvantummechanika – az utóbbi valamilyen alapvető változtatás nélkül, amely R-et „tényleges” folyamattá tenné – soha nem képes megmagyarázni azt, hogyan gondolkodunk.
10. Hol rejtőzik az ész fizikája?
Mire való az értelem?
Az értelem–test probléma vizsgálatánál általában két különálló kérdésre összpontosul a figyelem: „Hogyan hozhat létre tudatosságot egy anyagi objektum (egy agy)?” – és megfordítva: „Hogyan lehetséges, hogy a tudat akaratának működése által ténylegesen befolyásolja az anyagi objektumok (fizikailag nyilvánvalóan determinált) mozgását?” E kettő az értelem–test probléma passzív és aktív oldala. Úgy tetszik, „értelmünkben” (vagy inkább „tudatosságunkban”) van egy nem anyagi „dolog”, amelyet egyrészt az anyagi világ idéz elő, másrészt amely befolyásolni képes az anyagi világot. Azonban itt, az utolsó fejezet elején inkább egy némileg eltérő és talán tudományosabb kérdéssel szeretnék foglalkozni, amely mind az aktív, mind a passzív probléma szempontjából lényeges – abban a reményben, hogy megválaszolása egy kissé közelebb visz bennünket a filozófia ezen évszázados alapproblémájának jobb megértéséhez. Kérdésem a következő: „Milyen kiválasztó előnyt nyújt a tudatosság annak, aki ténylegesen rendelkezik vele?”
A kérdés ilyen megfogalmazásában van néhány hallgatólagos feltevés. Először is a hit, hogy a tudatosság tudományosan leírható „dolog”. A feltevés az, hogy ez a „dolog” ténylegesen „csinál valamit” – és mi több, amit csinál, az birtokolójának hasznos, tehát egy tudat nélküli, de egyébként egyenértékű teremtmény kevésbé hatékony módon viselkedne. Másrészt azt is lehet gondolni, hogy a tudatosság egy eléggé alapos szabályozó rendszer birtoklásának csupán passzív velejárója, és önmagában valójában nem „csinál” semmit. (Feltehetően ez volna a nézete például az EMI híveinek.) Egy másik lehetőség esetleg az, hogy a tudatosság jelenségének van valami isteni vagy más, titokzatos – esetleg előttünk még nem ismert, teleologikus – célja, és e jelenségnek csupán a természetes kiválasztódás fogalmai keretében történő tárgyalása teljesen eltévesztené e „célt”. Gondolkodásmódomnak valamivel jobban megfelelne az effajta érvelés egy tudományosabb változata, nevezetesen az emberszabású elv, amely azt állítja, hogy világegyetemünk természetét erősen megszorítja az a követelmény, hogy megfigyeléséhez olyan érző lények jelenléte szükséges, mint amilyenek magunk vagyunk. (Erre az elvre futólag már hivatkoztam a 8. fejezetben, és később még visszatérek rá.)
E kérdések legtöbbjével a kellő időben majd foglalkozunk, ám először meg kell jegyeznünk, hogy az „értelem” kifejezés egy kissé félrevezető, amikor az „értelem–test” problémát emlegetjük. Gyakran beszélünk a „tudatalatti értelemről”. Ez azt mutatja, hogy az „értelem” és a „tudatosság” kifejezéseket nem tekintjük egymás szinonimáinak. Amikor a tudatalatti értelemről beszélünk, akkor esetleg homályos képünk van „valakiről ott hátul”, aki a színfalak mögött cselekszik, de közvetlenül rendszerint nem befolyásolja azt, amit felfogunk (kivéve talán az álmokat, a hallucinációkat, a rögeszméket vagy a freudi elszólásokat). A tudatalatti értelemnek esetleg megvan a saját tudatossága, csak ezt rendszerint egészen elválasztjuk értelmünk azon részétől, amelyre általában úgy hivatkozunk, hogy „mi magunk”.
Lehet, hogy az egész nem annyira erőltetett, mint amilyennek először tűnik. Vannak kísérletek, amelyek azt látszanak jelezni, hogy még akkor is lehet jelen valamiféle „tudatosság”, amikor a beteget teljes altatás közben operálják – abban az értelemben, hogy az akkor lezajló beszélgetések később „tudat alatt” befolyásolhatják az illetőt, és hipnózisban, mint amit valójában a műtét közben is „átélt”, olykor visszaidézhetők. Továbbmenve, olyan érzékelések, amelyeket a hipnotikus szuggesztió látszólag elzár a tudatosságtól, később újabb hipnózis alatt mint „tapasztaltak”, de valahogyan „máshol raktározottak”, felidézhetők (vö. Oakley és Eames 1985). Ezek a kérdések egyáltalán nem világosak számomra, bár nem hiszem, hogy helyes volna bármiféle közönséges „tudatosságot” tulajdonítani a tudatalatti értelemnek, és nem igazán kívánok ilyen fejtegetésekbe bocsátkozni. Mindazonáltal a tudatos és tudat alatti értelem szétválasztása biztosan kényes és bonyolult probléma, amelyre majd vissza kell térnünk.
Próbáljunk most, amennyire csak tudunk, egyenesen beszélni arról, mit értünk „tudatosságon”, és hogy mikor hisszük, hogy jelen van. Nem hiszem, hogy a megértésnek ebben a szakaszában bölcs dolog volna pontos meghatározásra törekednünk, nyugodtan támaszkodhatunk szubjektív benyomásainkra és intuitív józan eszünkre a tekintetben, mit jelent ez a kifejezés, és mikor valószínűsíthető, hogy a tudatosság tulajdonsága jelen van. Többé-kevésbé tudom, mikor vagyok tudatos, és úgy veszem, hogy más emberek nagyjából hasonlókat tapasztalnak, mint amiket én. Tudatosnak lenni, ahhoz, úgy látszik, valaminek kell tudatában lenni, egy érzékelésnek, fájdalomnak, melegnek, színpompás jelenetnek vagy zenei hangnak; vagy esetleg olyan érzésnek, mint a rejtély, kétségbeesés vagy boldogság; tudatomban lehet valamilyen múltbéli tapasztalat emléke, vagy az, hogy megértem másvalaki szavait, vagy saját új elképzeléseim; vagy akarhatok tudatosan beszélni vagy más cselekvést végrehajtani, például helyemről felállni. Tehetek egy „lépést vissza” is, és tudatosulhatnak bennem az ilyen szándékok, vagy a fájdalom érzése, vagy az emlékezés, vagy a megértés; vagy akár saját tudatosságom. Elalhatok, és bizonyos fokig még mindig tudatos lehetek, feltéve, hogy valamit álmodom; vagy esetleg az ébredés kezdetén tudatosan befolyásolhatom az álom irányát. Kész vagyok azt gondolni, hogy a tudatosságnak fokozatai vannak, és nem egyszerűen olyan valami, amely vagy van, vagy nincs. A „tudatosság” és „tudomás” szavakat lényegében egymás szinonimáinak tekintem (bár a „tudomás” talán valamivel passzívabb), ellenben az „értelem” és „lélek” szavaknak másodlagos jelentései is vannak, amelyek jelenleg jóval kevésbé definiálhatók. Lesz elég bajunk a „tudatosság” kifejezéssel önmagában is, ezért remélem, az Olvasó megbocsátja, ha az „értelem” és „lélek” további taglalásába nem megyek bele!
Ott van még a kérdés, hogy mit értünk az „intelligencia” kifejezésen. Ez az végül is, amivel a MI-kutatók foglalkoznak a „tudatosság” talán ködösebb problémája helyett. Alan Turing (1950) híres cikkében (vö. 1. fejezet) nem is utalt ilyen közvetlenül a „tudatosságra”, hanem a „gondolkodásra”, és a címben az „intelligencia” szó szerepelt. Ahogy én nézem a dolgokat, úgy az intelligencia kérdése a tudatosságéhoz képest másodlagos. Nem gondolom, hagy azt hinném, ténylegesen jelen lehet igazi intelligencia, hacsak nem párosul tudatossággal. Másrészt viszont, ha valóban az a helyzet, hogy a MI-kutatók képesek úgy szimulálni az intelligenciát, hogy tudatosságról nincs szó, akkor nem tekinthető kielégítőnek, ha nem definiáljuk az „intelligenciát”, beleértve az ilyen szimulált intelligenciát is. Ebben az esetben az „intelligencia” kérdése nem tartozna igazán mostani témánkhoz. Elsősorban a „tudatossággal” foglalkozunk.
Amikor kinyilvánítom hitemet, hogy az igazi intelligencia megköveteli a tudatosságot, akkor hallgatólagosan azt sugallom (minthogy nem hiszek az EMI állításában, mely szerint egy algoritmusnak csupán végrehajtása előidézi a tudatosságot), hogy az intelligencia nem szimulálható megfelelően algoritmikus módon, azaz számítógéppel a manapság használt értelemben. (Lásd a „Turing-próba” tárgyalását az 1. fejezetben.) Rövidesen erős érveket hozok fel amellett (lásd különösen a matematikai gondolkodás tárgyalását három szakasszal később), hogy a tudatosság működésében egy alapvetően nemalgoritmikus alkotórésznek is lennie kell.
Nézzük meg most azt a kérdést, hogy van-e működési különbség a tudatos és az azzal egyébként „ekvivalens” dolog között, amely nem az. Mindig leleplezi-e jelenlétét a tudatosság? Szeretném azt gondolni, hogy e kérdésre a válasz szükségszerűen „igen”. E hitemet azonban aligha bátorítja az egyetértésnek a teljes hiánya abban, hogy hol lelhető fel tudatosság az állatvilágban. Egyesek semmiféle állatnak nem engedik meg a tudat birtoklását (és egyesek még az i. e. 1000 előtt élt emberi lényeknek sem, vö. Janes 1980), míg mások tudatosságot tulajdonítanak egy rovarnak, egy féregnek, sőt talán még egy sziklának is! A magam részéről nagyon kétlem, hogy egy rovar vagy féreg – a szikláról nem is beszélve – számottevően, ha egyáltalán, tudatos lehet, ám az emlősök általánosságban némi valódi tudatosság benyomását keltik bennem. Az egyetértés e hiányából legalábbis arra kell következtetnünk, hogy a tudat megnyilvánulásának nincs általánosan elfogadott ismertetőjele. Lehetséges, hogy van ismérve a tudatos viselkedésnek, de nem egyetemesen elismert. Mindenesetre csak az aktív szerep az, ami jelezhetne. Nehéz látni, hogyan volna közvetlenül megállapítható a tudatosság puszta jelenléte az aktív oldal nélkül. Ezt megdöbbentően igazolják azok a tények, hogy az 1940-es években a kuráre kábítószert használták „altatóként” fiatal gyermekeken végrehajtott műtétekben – noha e szernek az igazi hatása abban áll, hogy megbénítja az izmok motoros idegeinek működését, így e szerencsétlen gyermekek tényleges haláltusájáról a sebész ott nem szerezhetett tudomást (vö. Dennett 1978, 5. fejezet).
Nézzük meg a tudatosság lehetséges aktív szerepét. Szükségszerűen az-e a helyzet, hogy a tudatosság képes működésben felismerhető aktív szerepre – és ez olykor valóban be is következik? Okaim, hogy ezt higgyem, némileg különbözőek. Először is ott van az, hogy „józan eszünket” használva gyakran érezzük úgy, hogy közvetlenül felfogjuk valaki más tudatosságát. Ez a benyomásunk nem nagyon szokott tévedni.178 Míg egy tudatos személy nem feltétlenül látszik annak (mint a kurárével kábított gyermekek), egy nem tudatosról nem valószínű, hogy tudatosnak látszik! Ezért valóban kell legyen valamilyen, a tudatosságra jellemző viselkedésmód (ha nem is mindig annak bizonysága), amelyre „józan eszű intuícióink” révén érzékenyek vagyunk.
Másodszor tekintsük a természetes kiválasztódás könyörtelen folyamatát. Nézzük ezt a folyamatot annak a ténynek a fényében, hogy amint azt az előző fejezetben láttuk, az agynak nem minden tevékenysége köthető közvetlenül a tudatossághoz. Valóban: az „öregebb” kisagy – a neuronsűrűségben mutatkozó hatalmas fölényével – nagyon összetett műveleteket látszik végrehajtani mindenféle közvetlen tudatosság nélkül. A Természet mégis úgy döntött, hogy kifejleszt olyan érző lényeket, mint mi vagyunk, és nem elégedett meg azokkal a teremtményekkel, amelyek egy teljesen tudattalan szabályozó mechanizmus irányítása alatt létezhetnek. Ha a tudatosság nem szolgál kiválasztódási célokat, akkor miért bajlódott a Természet a tudatos agyak kifejlesztésével, amikor a nem érző „automataagyak”, mint a kisagy, láthatóan ugyanúgy megtették volna?
Továbbmenve: van egy egyszerű okunk, hogy azt higgyük, a tudatosságnak kell legyen valamilyen aktív hatása, még ha nem is jár vele kiválasztódási előny. Mi az oka annak, hogy az olyan lények, mint mi, olykor – különösen amikor az ilyen dolgokon töprengenek – az „önmagukról” való kérdésekkel gyötrődnek? (Majdnem azt mondhatnám: „Miért olvassa Ön ezt a fejezetet?” vagy „Miért éreztem erős vágyat, hogy könyvet írjak erről a témáról?”) Nehéz elképzelni, hogy egy teljesen tudattalan automata ilyen dolgokra vesztegetné idejét? Minthogy viszont a tudatos lények időről időre láthatóan ilyen furcsa módon cselekednek, ezért viselkedésük eltér attól, ahogy viselkednének, ha nem volnának tudatosak – tehát a tudatosságnak van aktív hatása! Természetesen nem volna probléma szándékosan úgy programozni egy számítógépet, hogy ilyen furcsa viselkedést mutasson (lehetne például úgy, hogy morfondírozzon: „Ó kedvesem, mi az, hogy élet? Miért vagyok én itt? Mi a csuda ez az „önmagam”, amit érzek?”). De miért bajlódna a természetes kiválasztódás az ilyen fajjal, amikor a dzsungel könyörtelen törvénye bizonyára régen kiirtotta volna az ilyen haszontalan értelmetlenséget!
Nekem világosnak látszik, hogy a tűnődés és töprengés, amibe elmerülünk, amikor (esetleg időlegesen) filozófusokká válunk, nem olyan dolgok, amelyek önmagukért valóak, hanem (a természetes kiválasztódás szempontjából) a szükséges „málha”, amelyet cipelniük kell a valóban tudatos lényeknek, akiknek tudatosságát a természetes kiválasztódás eredményezte, de valami egészen különböző és feltehetően nagyon erőteljes okból. Olyan poggyász ez, amely nem túlságosan ártalmas, és amelyet, azt sejtem, könnyen (bár talán fukarul) szültek meg a természetes kiválasztódás fékezhetetlen erői. Alkalmanként, talán amikor szerencsés fajtánk olykor a békét és jólétet élvezi, és nem kell mindig az elemekkel (vagy szomszédainkkal) a túlélésért küzdeni, a poggyász tartalmának kincsein kezdünk tűnődni és kíváncsiskodni. Amikor másokat ilyen különös, filozofikus módon látunk viselkedni, akkor győződünk meg arról, hogy magunktól eltérő egyéniségekkel van dolgunk, akiknek szintén van értelmük.
178 Legalábbis a mai számítógép-technológia mellett (lásd a Turing-próba tárgyalását az 1. fejezetben).
Mit tesz valójában a tudatosság?
Fogadjuk el, hogy a tudatosság jelenléte egy teremtményben ténylegesen kiválasztódási előnyöket biztosít. Mi lehet ilyen előny? Hallottam olyan véleményt, hogy a tudatosság előnyt jelenthet a ragadozó számára, mert magát az áldozat „helyébe képzelve”, megpróbálja megsejteni, mit fog az valószínűen tenni a következő pillanatokban.
Az elképzelésben részigazság lehet, de bennem kételyt támaszt. Először is feltételezi a tudatosság bizonyos csíráját magánál az áldozatnál, minthogy aligha segítene, ha a ragadozó magát automatának képzelné, mert egy automata – a definíció szerint nem tudatos – nem olyan valami, ami egyáltalán „lenni” képes! Mindenesetre ugyanolyan jól el tudom képzelni, hogy egy teljesen tudattalan automata ragadozó programjának része lehet olyan szubrutin, amely automata zsákmányának tényleges programja. Nem látom logikailag szükségszerűnek, hogy a tudatosság egyáltalán belépjen ebbe a ragadozó–zsákmány kapcsolatba.
Azt természetesen nehéz látni, hogyan lehetnek a természetes kiválasztódás véletlenszerű folyamatai elég okosak ahhoz, hogy egy automata ragadozónak odaadják az áldozat programjának egy teljes másolatát. Ez sokkal inkább hangzik kémkedésnek, mint természetes kiválasztódásnak! Egy részprogram pedig (olyan értelemben, mint a Turing-gép „szalagjának” egy része vagy a szalagot megközelítő valami) aligha biztosít komoly kiválasztódási előnyt a ragadozónak. Szükségesnek látszik az egész szalag vagy legalább valamely önálló rész valószínűtlen birtoklása. Így, alternatívaként, lehet némi részigazság az elképzelésben, hogy a ragadozó – zsákmány gondolatmenetből inkább a tudatosság bizonyos eleme, mint egy számítógépes program következtethető ki. Ám ez nem a valódi kérdést látszik megcélozni, azt, hogy mi is az igazi különbség a tudatos és a „programozott” cselekvés között.
A felvázolt elképzelés a tudatosság egy gyakran emlegetett felfogásához látszik kapcsolódni, amely szerint egy rendszer akkor van „tudatában” valaminek, ha van modellje arról a dologról, és akkor válik „ön-tudatossá”, ha önmagáról van modellje. Ám egy számítógépes program, amely tartalmazza (mondjuk szubrutinként) egy másik számítógépes program valamilyen leírását, nem lesz tudatában e másodiknak; és az ön-hivatkozás sem ad ön-tudatosságot. A gyakran elhangzó állítások ellenére az effajta meggondolások, véleményem szerint, aligha érintik a tudatosság és ön-tudatosság valódi problémáit. Egy videokamera nincs tudatában az általa rögzített jeleneteknek; és ha tükör elé helyezzük, attól még nem lesz ön-tudatos (10.1. ábra).
Más vonalat óhajtok követni. Láttuk, hogy nem minden agyunk által végzett tevékenység köthető össze a tudatossággal (és különösen a kisagy működése látszik tudatalattinak). Mi az, amit tudatos gondolkodással meg tudunk tenni, de tudattalanul nem? A problémát nehezebben megfoghatóvá teszi az a tény, hogy bármit, ami eredetileg láthatóan tudatosságot követel, meg is tudunk tanulni, és később (talán a kisagy irányításával) tudattalanul is el tudunk végezni. A tudatosságra olyan helyzetek kezeléséhez van szükség, ahol új ítéleteket kell kialakítanunk, és ahol a szabályokat korábban még nem fektették le. Nehéz nagyon pontos különbséget tenni a tudatosságot megkövetelő és az azt meg nem követelő szellemi tevékenységek között. Esetleg, ahogy azt az EMI hívei (és mások is) állítják, amikor „új ítéleteket alkotunk”, akkor is jól meghatározott algoritmikus szabályokat alkalmazunk, csak homályosakat és „magas szintűeket”, amelyek működéséről nincs tudomásunk. Úgy gondolom azonban, hogy az előszeretettel használt terminológia, amely különbséget tesz tudatos és tudatalatti szellemi tevékenységünk között, legalábbis sugallja a nemalgoritmikus/algoritmikus szétválasztást:
Tudatosság szükséges „józan ész” „az igazság megítélése” „megértés” „művészi értékelés” | Tudatosság nem szükséges „automatikus” „értelem nélküli szabálykövetés” „programozott” „algoritmikus” |
Lehet, hogy ez a szétválasztás nem mindig elég világos, különösen azért, mert tudatos ítélkezésünkbe sok nem tudatos tényező is belejátszik: tapasztalat, intuíció, előítélet, még a rendes logikánk használata is. Azonban maguk az ítéletek, állítom, tudatosságunk működésének megnyilvánulásai. Ezért úgy gondolom, hogy amíg az agy tudattalan tevékenységei algoritmikus folyamatok, a tudatosság működése ettől egészen eltérő, olyan módon történik, amely semmiféle algoritmussal nem írható le.
Némileg mulatságos, hogy az itt előadott nézeteim majdnem megfordításai másokéinak, amelyekkel sokszor találkozom. Gyakran érvelnek úgy, hogy a tudatos értelem viselkedik érthető, „racionális” módon, és a tudattalan az, amely titokzatos. A MI-val dolgozó emberek gyakran állítják, hogy amennyiben valaki képes tudatosan megérteni egy gondolatmenetet, akkor azt is látja, hogyan kell azt egy számítógéppel elvégeztetni; a rejtélyes nem tudatos folyamatok azok, amelyekkel (egyelőre!) nem tudjuk, mit kezdjünk. Szerintem a tudatalatti folyamatok nyugodtan lehetnek algoritmikusak, csak nagyon bonyolultak, amelyeket roppant nehéz részletesen kibogozni. A teljesen tudatos gondolkodás, amely ésszerűen egészen logikus, megint (gyakran) formálissá tehető, mint amely algoritmikus, csak egészen eltérő szinten. Most nem a belső működésre (neuronok tüzelésére stb.) gondolok, hanem egész gondolatok kezelésére. E gondolatkezelés olykor algoritmikus jellegű (mint a korai logikában: az ókori görögöknek Arisztotelész által formába öntött szillogizmusai, vagy a matematikus George Boole szimbolikus logikája; vö. Gardner 1958), olykor nem az (mint a Gödel-tétel és a 4. fejezet egyes példái mutatják). Az ítéletalkotás, amely állításom szerint a tudatosság ismertetőjele, maga valami olyan, amelyről a MI-kutatók nem tudnák, hogyan programozzák számítógépbe.
Olykor azt az ellenvetést kapom, hogy ezen ítéletek kritériumai végül is nem tudatosak, miért tulajdonítom akkor az ítéleteket a tudatosságnak? Ám ez az ellenvetés éppen azon a ponton hibás, amelyről most beszélek. Nem azt mondom, hogy tudatosan megértjük, hogyan alakítjuk ki tudatos benyomásainkat és ítéleteinket. Ezzel összekeverném a szinteket, amelyekre éppen az előbb utaltam. A tudatos benyomásaink alapjait képező okok nem közvetlenül hozzáférhetőek a tudatosság számára. Ezeket mélyebb fizikai szinten kellene keresnünk, nem a tudatunkban lévő tényleges gondolatokén. (A későbbiekben megtorpedózok egy javaslatot!) Maguk a tudatos benyomások a (nemalgoritmikus) ítéletek.
Az előző fejezeteken végighúzódott az a gondolat, hogy tudatos gondolkodásunkban látszik valami nemalgoritmikus. Különösen a 4. fejezetben és ebben is főleg a Gödel-tétel alapján levont egyik következtetés volt az, hogy legalábbis a matematikában, a tudatos elmélkedés olykor képessé tesz arra, hogy megállapítsuk egy állítás igazságát olyan módon, ahogy arra egy algoritmus nem képes. (Ezt mindjárt részletesen kifejtem.) Valójában az algoritmusok önmagukban soha nem derítenek ki igazságot! Ugyanolyan könnyű volna olyan algoritmust csinálni, amely csak hamisságokat produkál, mint olyat, amely igazságokat. Külső meglátásokra van szükség ahhoz, hogy eldöntsük, érvényes-e egy algoritmus vagy sem (erről többet később). Az az állításom, hogy éppen igazság és hamisság (és szépség és csúnyaság!) szétválasztásának ez a képessége az, ami megfelelő körülmények között a tudatosság ismertetőjegye.
Szeretném azonban világossá tenni, hogy nem gondolok valamiféle „mágikus” megsejtésre. A tudatosság egyáltalán nem segít a lottószámok kitalálásában! Azokra az ítéletekre utalok, amelyeket tudatos állapotban folyamatosan készítünk, összesítve minden lényeges tényt, érzékszervi benyomást, emlékezetben lévő tapasztalatot, ezeket egymáshoz képest súlyozzuk – alkalmanként még ihletett ítéletek is születhetnek. A lényeges ítéletekhez elvileg van elegendő információ, de az ítéletalkotás folyamata, az adatok tengeréből a szükségesek kihalászása, ez olyasmi lehet, amire nincs világos algoritmikus eljárás – vagy ha mégis, akkor az a gyakorlatban esetleg nem használható. Előfordulhat olyan helyzet, hogy ha egyszer az ítélet megszületett, akkor már sokkal inkább algoritmikus (vagy még egyszerűbb) folyamat annak ellenőrzése, hogy az ítélet pontos-e, mint magának az ítéletnek a kialakítása. Sejtésem szerint a tudatosság ilyen körülmények között úgy teszi meg a magáét, hogy felidézi a megfelelő ítéleteket.
Miért mondom azt, hogy a tudatosság ismertetőjegye az ítéletek nemalgoritmikus kialakítása? Az okok egy része matematikusi tapasztalatomból származik. Egyszerűen nem bízom a tudatalatti algoritmikus tevékenységemben, amikor tudatom nem megfelelően irányítja. Az algoritmussal mint algoritmussal gyakran semmi baj nincsen egy elvégzendő számításban, csak éppen az-e a helyes algoritmus a kéznél lévő problémára? Egyszerű példa az, hogy megtanuljuk két szám összeszorzásának és egymással való osztásának is az algoritmikus szabályait (lehet, hogy valaki szívesebben használja erre algoritmikus zsebszámológépét), de honnan tudjuk, hogy az előttünk lévő problémában szorozni vagy osztani kell-e a számokkal? Ehhez gondolkodni kell, és tudatos ítéletet alkotni. (Hamarosan látni fogjuk, miért kell az ilyen ítéleteknek, legalább olykor, nemalgoritmikusaknak lenniük!) Természetesen ha egyszer nagyszámú hasonló problémát megoldottunk, akkor a döntés, hogy szorozni kell-e vagy osztani, másodlagossá válhat, és algoritmikusan végezheti – feltehetően a kisagy. Ebben a szakaszban a tudatosságra többé nincs szükség, és nyugodtan engedhetjük értelmünket más dolgokhoz vándorolni és azokon elmélkedni – noha időről időre szükséges lehet, hogy ellenőrizzük, nem csúszott-e félre (esetleg csak nagyon finoman) az algoritmus.
Ugyanez a dolog történik meg folyamatosan a matematikai gondolkodás minden szintjén. Amikor matematikát csinálunk, gyakran keresünk algoritmusokat, de a keresés maga nem látszik algoritmikus eljárásnak. Ha találunk megfelelő algoritmust, akkor a problémát bizonyos értelemben megoldottuk. Továbbmenve: a matematikai ítélet, hogy valamely algoritmus valóban pontos vagy megfelelő, olyan dolog, amely sok tudatos figyelmet igényel. Valami hasonlóról volt szó a matematika formális rendszereinek tárgyalásában a 4. fejezetben. Kiindulhatunk axiómákból, amelyekből változatos matematikai propozíciók származtathatók. Ez az eljárás valóban lehet algoritmikus, de a tudatos matematikus ítéletére van szükség, hogy eldöntse, megfelelőek-e az axiómák. Hogy ezek az ítéletek szükségszerűen nemalgoritmikusak, az világosabban ki fog derülni a következő utáni szakaszban elmondottakból. Ám mielőtt erre rátérnénk, nézzünk meg egy, talán jobban elterjedt nézetet arra vonatkozóan, hogy hogyan alakult ki, és mit csinál agyunk.
1./
Lehet, hogy ez a szétválasztás nem mindig elég világos, különösen azért, mert tudatos ítélkezésünkbe sok nem tudatos tényező is belejátszik: tapasztalat, intuíció, előítélet, még a rendes logikánk használata is. Azonban maguk az ítéletek, állítom, tudatosságunk működésének megnyilvánulásai. Ezért úgy gondolom, hogy amíg az agy tudattalan tevékenységei algoritmikus folyamatok, a tudatosság működése ettől egészen eltérő, olyan módon történik, amely semmiféle algoritmussal nem írható le.
Némileg mulatságos, hogy az itt előadott nézeteim majdnem megfordításai másokéinak, amelyekkel sokszor találkozom. Gyakran érvelnek úgy, hogy a tudatos értelem viselkedik érthető, „racionális” módon, és a tudattalan az, amely titokzatos.
2./
A tudatos benyomásaink alapjait képező okok nem közvetlenül hozzáférhetőek a tudatosság számára. Ezeket mélyebb fizikai szinten kellene keresnünk, nem a tudatunkban lévő tényleges gondolatokén. (A későbbiekben megtorpedózok egy javaslatot!) Maguk a tudatos benyomások az (nemalgoritmikus) ítéletek.
Az előző fejezeteken végighúzódott az a gondolat, hogy tudatos gondolkodásunkban látszik valami nemalgoritmikus. Különösen a 4. fejezetben és ebben is főleg a Gödel-tétel alapján levont egyik következtetés volt az, hogy legalábbis a matematikában, a tudatos elmélkedés olykor képessé tesz arra, hogy megállapítsuk egy állítás igazságát olyan módon, ahogy arra egy algoritmus nem képes.
Az algoritmusok természetes kiválasztódása?
Ha feltételezzük, hogy az emberi agy tudatos vagy tudattalan működése csupán egy nagyon bonyolult algoritmus végrehajtása, akkor meg kell kérdeznünk, honnan származik ez a rendkívül hatásos algoritmus. A szokásos válasz persze a „természetes kiválasztódás”. Ahogy az aggyal bíró teremtmények fejlődtek, a hatékonyabb algoritmussal rendelkezőknek jobb esélyük volt a fennmaradásra, és ezért több utódot hoztak létre. Az utódok szintén jobb algoritmusokat hajtottak végre, mint távolabbi rokonaik, minthogy szüleiktől örökölték ezek alkotórészeit; így az algoritmusok fokozatosan javultak – nem szükségképpen egyenletesen, fejlődésükben jelentős hullámzások lehettek –, míg elérték azt a figyelemre méltó állapotot, amelyet az emberi agyban megtalálunk (lásd Dawkins 1986).
Némi igazság még az én nézőpontom szerint is kell legyen ebben a képben, mert úgy képzelem, hogy az agy tevékenységének jelentős része algoritmikus, és – ahogy arra az Olvasó az előző okfejtésből következtethet – komolyan hiszek a természetes kiválasztódás erejében. Nem látom azonban, hogyan fejleszthet ki a természetes kiválasztódás önmagában olyan algoritmusokat, amelyekben tudatos ítéletek lehetnek más algoritmusok érvényességéről, pedig a helyzet, úgy látszik, ez.
Képzeljünk el egy közönséges számítógépprogramot. Hogyan jön ez létre? Nyilván nem (közvetlenül) természetes kiválasztódással! Számítógép-programozók gondolják ki és ellenőrzik, hogy helyesen végzi-e el azokat a feladatokat, amelyekre tervezték. (Valójában a legtöbb bonyolult számítógépprogramban vannak hibák – rendszerint aprók, de gyakran olyan finomak, hogy csak szokatlan körülmények között derülnek ki. Az ilyen hibák létezése nem befolyásolja lényegesen érvelésemet.) Olykor egy számítógépprogram, mondjuk egy „mesterprogram” „írhat” egy másikat, de a mesterprogram maga akkor is az emberi leleményesség és meglátás terméke; vagy lehet, hogy a program olyan alkotórészekből áll össze, amelyek közül egyesek más számítógépprogramok termékei. Ám a program érvényességéért és igazi céljáért végül is minden esetben (legalább) egy emberi tudat a felelős.
Lehet persze azt képzelni, hogy nem szükségképpen ez a helyzet, és hogy elegendően hosszú idő alatt a számítógépprogramok maguktól fejlődhetnek a természetes kiválasztódás bizonyos folyamatában. Ha elhisszük, hogy a programozók tudatosságának működése egyszerűen algoritmusokban nyilvánul meg, akkor azt is hinnünk kell, hogy az algoritmusok éppen ilyen módon fejlődtek. Azonban engem aggaszt az, hogy egy algoritmus érvényességének eldöntése nemalgoritmikus folyamat! Erről valamit már láttunk a 2. fejezetben. (A kérdést, hogy egy Turing-gép megáll-e vagy sem, nem lehet algoritmikusan eldönteni.) Hogy eldöntsük, működni fog-e egy algoritmus vagy sem, ahhoz meglátásokra van szükségünk, és nem egy másik algoritmusra.
Mindazonáltal, még mindig el lehet képzelni olyan természetes kiválasztódási folyamatot, amely hatásosan termel közelítőleg érvényes algoritmusokat. Én magam azonban nagyon nehezen tudnám ezt elhinni. Az ilyen jellegű kiválasztódási folyamat nem hathatna közvetlenül az algoritmusok működésének alapjait képező ideákra, hanem csak az algoritmusok kimenetére.179 Ez nem egyszerűen rendkívül rossz hatásfokú; úgy vélem, teljesen működésképtelen. Elsősorban csak a kimenetét vizsgálva nem könnyű megállapítani, mi is egy algoritmus. (Könnyű volna két egészen különböző Turing-gépet készíteni, amelyek kimeneti szalagjai nem különböznek mondjuk a 265536 helyig – ezt a különbséget a világegyetem teljes története során sem lehetne észrevenni!) Továbbmenve: egy algoritmus legcsekélyebb „mutációja” (mondjuk egy parányi változás egy Turing-gép megadásában vagy bemeneti szalagján) teljesen haszontalanná teheti azt, és nehéz látni, hogyan keletkezhetnének az algoritmusokban tényleges javítások ilyen véletlenszerű módon. (Még a szándékos javítás is nehéz a megfelelő „jelentések” ismerete nélkül. Ezt különösen igazolják azok a nem ritka esetek, amikor egy nem megfelelően dokumentált és bonyolult számítógépprogramot javítani vagy változtatni kell, és az eredeti programozó már eltávozott vagy esetleg meghalt. Ahelyett, hogy kibogoznánk az összes különféle jelentést és intenciót, amelyekre a program hallgatólagosan épül, valószínűleg könnyebb kidobni, és az egészet újra kezdeni!)
Talán kigondolhatók az algoritmusok megadásának sokkal „egészségesebb” módjai, amelyek nem illethetők az előbbi bírálattal. Tulajdonképpen ez az, amit magam is mondok. Az „egészséges” megadások az algoritmusok alapjait képező ideák. Ezek azonban olyan dolgok, amelyek megnyilvánulásához, amennyire tudjuk, tudatos értelemre van szükség. Visszajutottunk a problémához, hogy mi is valójában a tudatosság, és mit tud megtenni, amire a tudatalatti objektumok képtelenek – és hogy a csudában volt elég bölcs a természetes kiválasztódás, hogy kifejlesztette ezt a legnagyszerűbb minőséget.
A természetes kiválasztódás termékei valóban megdöbbentőek. Az a kevés, amit az emberi agy – és tulajdonképpen bármilyen más élőlény – működéséről megtudtam, tisztelettel és ámulattal tölt el. Egyetlen neuron működése is rendkívüli, de egészen csodálatos módon szerveződnek össze, hatalmas számú kiépített kapcsolat áll készen születéskor minden, a későbbiekben elvégzendő feladatra. Nem csupán a tudatosság maga lenyűgöző, de az egész felszereltség is, amelynek ki kell azt szolgálnia!
Ha valaha kiderítjük annak részleteit, milyen minőség teszi lehetővé, hogy egy fizikai objektum tudatossá váljék, akkor elképzelhetően magunk is képesek lehetünk ilyen objektumokat készíteni – bár lehet, hogy nem minősülnek majd „gépeknek” a szónak abban az értelmében, ahogy azt ma használjuk. Elképzelhető, hogy ezek az objektumok óriási fölényben lesznek velünk szemben, minthogy speciálisan arra lehet majd tervezni őket, hogy tudatosak legyenek. Nem egyetlen sejtből kell kinőniük. Nem kell cipelniük származásuk „málháját” (az agy vagy test régi és „haszontalan” részeit, amelyek továbbélnek bennünk csupán távoli eredetünk „véletlenei” miatt). Látva ezeket az előnyöket elképzelhető, hogy az ilyen objektumoknak sikerülhet kiszorítaniuk az emberi lényeket arról a területről, ahol az algoritmikus számítógépek (a magaméhoz hasonló vélemények szerint) szolgai engedelmességre vannak ítélve.
Azonban a tudatosság problémája még sokkal tágabb lehet. Tudatosságunk esetleg valamilyen módon függvénye örökségünknek, a tényleges fejlődés mögöttünk lévő ezermillió évének. Az én gondolatmenetemben még mindig van valami titokzatos a fejlődés körül, ahogy láthatóan jövőbeli célok felé „tapogatózik”. A dolgok, legalábbis úgy látszik, a „kelleténél” valamivel jobban szervezik önmagukat, fejlődés és a természetes kiválasztódás alapján. Lehet, hogy e látszat csalóka. A fizika törvényeinek működése körül látszik valami, ami lehetővé teszi, hogy a természetes kiválasztódás sokkal hatásosabb folyamat legyen, mint lenne más, önkényes törvények mellett. Az eredmény, a látható „intelligens tapogatózás” érdekes kérdés, később röviden még visszatérek rá.
179 Felvetődik az a fogas kérdés is, hogy ekvivalensnek kell-e tekintenünk két algoritmust akkor, ha csupán kimeneteik azonosak, a tényleges számítások azonban nem. Lásd 2. fejezet.
1./
Ha valaha kiderítjük annak részleteit, milyen minőség teszi lehetővé, hogy egy fizikai objektum tudatossá váljék, akkor elképzelhetően magunk is képesek lehetünk ilyen objektumokat készíteni – bár lehet, hogy nem minősülnek majd „gépeknek” a szónak abban az értelmében, ahogy azt ma használjuk. Elképzelhető, hogy ezek az objektumok óriási fölényben lesznek velünk szemben, minthogy speciálisan arra lehet majd tervezni őket, hogy tudatosak legyenek. Nem egyetlen sejtből kell kinőniük. Nem kell cipelniük származásuk „málháját” (az agy vagy test régi és „haszontalan” részeit, amelyek továbbélnek bennünk csupán távoli eredetünk „véletlenei” miatt). Látva ezeket az előnyöket elképzelhető, hogy az ilyen objektumoknak sikerülhet kiszorítaniuk az emberi lényeket arról a területről, ahol az algoritmikus számítógépek (a magaméhoz hasonló vélemények szerint) szolgai engedelmességre vannak ítélve.
A matematikai meglátás nemalgoritmikus természete
Mint korábban már említettem, annak a vélekedésnek az okát, hogy a tudatosság az igazságítéleteket nemalgoritmikus módon képes befolyásolni, jelentős mértékben a Gödel-tétel körüli megfontolások szolgáltatják. Ha látjuk, hogy a matematikai ítéletek kialakításában, ahol a számítás és a szigorú bizonyítás két annyira fontos tényező, a tudatosság szerepe nemalgoritmikus, akkor ez bizonyára meggyőzhet bennünket, hogy ilyen nemalgoritmikus összetevő lényeges lehet a tudatosság szerepében általánosabb (nem matematikai) körülmények között is.
Idézzük vissza a Gödel-tétel bizonyításánál és a kiszámíthatóssággal való kapcsolatánál elhangzott érvelést. Ott megmutattuk, hogy bármilyen (elegendően széles körű) algoritmust is használ egy matematikus a matematikai igazság megállapítására – vagy, ami ugyanazt jelenti, bármilyen formális rendszert is fogad el az igazság feltételeinek rögzítésére –, mindig lesznek matematikai propozíciók, mint a rendszer Pk(k) explicit Gödel-propozíciója (4. fejezet), amelyekre algoritmusa nem tud választ adni. Ha a matematikus értelmének működése teljesen algoritmikus, akkor az ítéleteinek kialakítására ténylegesen használt algoritmus (vagy formális rendszer) nem képes kezelni a személyes algoritmusa által készített Pk(k) propozíciót. Mindazonáltal (elvileg) mi láthatjuk, hogy Pk(k) igaz! Ez ellentmondásra vezet, mert ezt ő is képes kellene legyen látni. Talán ez azt jelzi, hogy a matematikus egyáltalán nem is használt algoritmust!
Ám hogy ténylegesen meggyőzzük magunkat Pk(k) igazságáról, tudnunk kellene, mi a matematikus algoritmusa, és meg kellene győződnünk annak érvényességéről is, mert ezzel jutunk el a matematikai igazsághoz. Az EMI hívei gyorsan rámutatnának, hogy ha a matematikus fejében nagyon bonyolult algoritmust használ, akkor nem volna esélyünk megtudni, mi az az algoritmus, ezért nem tudnánk felállítani annak Gödel-propozícióját, az érvényességéről való meggyőződésről nem is beszélve. Ez a fajta ellenvetés gyakran hangzik el az olyan állításokkal kapcsolatban, mint amilyet magam is tettem, hogy a Gödel-tétel azt jelzi, hogy az emberi matematikai ítéletek nemalgoritmikusak.180 Ám az ellenvetést nem találom meggyőzőnek. Tegyük fel egy pillanatra, hogy a matematikus emberek tudatos ítéleteiket a matematikai igazságról valóban algoritmikus módon hozzák meg. A Gödel-tételt felhasználva megpróbálunk ebből ellentmondásra jutni (reductio ad absurdum!).
Először azzal a lehetőséggel kell foglalkoznunk, hogy a különböző matematikusok az igazság eldöntésére nem ekvivalens algoritmusokat használnak. Ám a matematika egyik legmeglepőbb tulajdonsága (amivel talán egyedül áll a diszciplínák között), hogy a propozíciók igazsága absztrakt bizonyítással eldönthető! Egy matematikai bizonyítás, amely meggyőzi az egyik matematikust – feltéve, hogy nincs benne hiba –, meg fogja győzni a másikat is, mihelyt teljesen megérti azt. Ez a Gödel-típusú propozíciókra is igaz. Ha az első matematikus kész elfogadni egy speciális formális rendszer minden axiómáját és eljárási szabályát, mint amelyek csak igaz propozíciókat adnak, akkor kész kell legyen elfogadni a Gödel-propozíciót is mint igaz propozíciót. Pontosan ugyanez áll a második matematikusra is. A lényeg az, hogy a matematikai igazságot megállapító bizonyítások közölhetőek.181
Ezért nem különféle homályos algoritmusokról beszélünk, amelyek történetesen az egyes matematikusok fejében működnek, hanem egyetlen univerzálisan alkalmazott formális rendszerről, amely ekvivalens az összes matematikus algoritmusával a matematikai igazság megítélésében. Ám ez a feltételezett „univerzális” rendszer vagy algoritmus nem lehet egyike azoknak, amelyeket mi, matematikusok az igazság eldöntésére használunk! Mert ha az volna, akkor meg tudnánk alkotni annak Gödel-propozícióját, és azt is matematikai igazságnak ismernénk. Ezért arra a következtetésre jutunk, hogy az algoritmus, amelyet a matematikusok a matematikai igazság eldöntésére ténylegesen használnak, olyan bonyolult vagy homályos, hogy érvényessége soha nem derülhet ki számunkra.
Azonban ez ellene mond mindannak, ami a matematika! Matematikai örökségünk és neveltetésünk egész lényege az, hogy nem hajlunk meg homályos szabályok tekintélye előtt, amelyek megértésére reményünk sem lehet. Látnunk kell – legalább elvileg –, hogy egy bizonyítás minden lépése egyszerű és nyilvánvaló. A matematikai igazság nem valami rémisztően bonyolult dogma, amelynek érvényessége túlmegy felfogóképességünkön. Egyszerű és nyilvánvaló elemekből épül fel – és amikor megértjük azokat, igazságuk világos és mindenki által elismert.
Úgy gondolom, annyira otromba reductio ad absurdum áll előttünk, amilyet csak elérni remélhetünk tényleges matematikai bizonyítás hiányában. Az üzenet világos. A matematikai igazság nem olyan valami, amit pusztán algoritmus használatával megállapíthatunk. Hiszem azt is, hogy tudatosságunknak döntő szerepe van a matematikai igazság megértésében. Egy matematikai bizonyítás igazságát „látnunk” kell, hogy érvényességéről meggyőződjünk. Ez a „látás” a tudatosság igazi lényege. Jelen kell lennie mindig, amikor csak közvetlenül megértünk matematikai igazságot. Amikor meggyőzzük magunkat a Gödel-tétel érvényességéről, akkor nemcsak „látjuk” azt, hanem egyszersmind leleplezzük magának a „látási” folyamatnak nagyon is nemalgoritmikus természetét.
180 Lucas (1961) úgy érvel, hogy a Gödel-tétel következménye a nemkiszámíthatóság, míg Good (1969), Benacerraf (1967) és Bowie (1982) változatos ellenérveket hoznak fel.
181 Egyes Olvasókat zavarhatja az a tény, hogy a matematikusok körében valóban különböző nézőpontok léteznek. Emlékezzünk vissza a 4. fejezetben tárgyaltakra. A különbségek azonban nem nagyon kell foglalkoztassanak bennünket. Azok csupán a nagyon nagy halmazokra vonatkozó, különleges kérdésekben vannak, mi pedig korlátozhatjuk figyelmünket az aritmetikai propozíciókra (véges számú egzisztenciális és univerzális kvantorral), és akkor az előbbi tárgyalás alkalmazható. (Ez talán némileg túlzott kijelentés, mert a végtelen halmazoknál olykor tükrözési elvvel aritmetikai propozíciók származtathatók.) Ami a nagyon dogmatikus, a Gödel-immunis formalistát illeti, aki még azt sem ismeri el, hogy van olyan dolog, hogy matematikai igazság, róla egyszerűen nem veszek tudomást, minthogy az igazság megsejtésének tulajdonsága, amiről szó van, láthatóan nincs birtokában!
Ihlet, meglátás, eredetiség
Szeretnék néhány megjegyzést tenni az új meglátásának azokra az időnkénti felvillanásaira vonatkozóan, amelyeket ihletnek nevezünk. Olyan gondolatok és képek-e ezek, amelyek rejtélyes módon a nem tudatos értelemből jönnek, vagy valamilyen lényeges értelemben magának a tudatosságnak a termékei? Sok példát lehet idézni, nagy gondolkodók írták le ilyen irányú tapasztalataikat. Mint matematikus különösen más matematikusok ihletett és eredeti gondolataival foglalkozom, de azt hiszem, nagyon sok közös vonás van a matematika és más tudományok és a művészetek között. Kitűnő olvasmányként ajánlom az Olvasónak a nagyon neves francia matematikus, Jacques Hadamard klasszikus művét, A felfedezés pszichológiája a matematika területén című karcsú kis kötetet. Számos tapasztalatot idéz, amelyeket vezető matematikusok és más emberek ihletett állapotukról írtak le. Az egyik legismertebb Henri Poincarétől származik. Ő először leírja, milyen alapos és tudatos erőfeszítéseket tett az ún. Fuchs-függvények kutatásában, de zsákutcába jutott. Ekkor:
…Caenból, ahol laktam, geológiai kirándulásra mentem a Bányászati Iskola védnöksége alatt. Az utazás eseményei elfeledtették velem matematikai munkámat. Coutances-t elérve omnibuszra szálltunk, hogy eljussunk valahová. Abban a pillanatban, amikor a lépcsőre tettem a lábam, eszembe jutott valami, amire korábban egyáltalán nem gondoltam, az, hogy a Fuchs-függvények definiálására használt transzformációk azonosak a nemeuklideszi geometria transzformációival. A gondolatot nem ellenőriztem; nem lett volna időm rá, minthogy elfoglalva helyem az omnibuszban egy korábban már megkezdett beszélgetést folytattam, de teljesen biztos voltam a dologban. A visszaúton Caenbe a biztonság kedvéért már kényelmesen ellenőriztem az eredményt.
Ebben (és számos más, Hadamard által idézett) példában az a meglepő, hogy e bonyolult és rejtett gondolat láthatóan villanásként érte Poincarét, mialatt tudatos gondolatai egészen máshol jártak, és a helyességét illetően a teljes biztonság érzetével társult –, mint azt a későbbi számítás valóban igazolta. Világossá kell tennem, hogy az elképzelést egyáltalán nem könnyű szavakban megmagyarázni. Úgy képzelem, hogy megfelelő kifejtésére nagyjából egyórás szemináriumon kerülhetett sor szakértők előtt. Poincaré tudatába teljesen kész állapotban nyilván csak a korábbi sok hosszú órát kitevő alapos tudatos tevékenység következtében léphetett be, ezalatt a szóban forgó problémának már sok különböző oldalát kiismerte. Mégis, bizonyos értelemben, Poincarénak a buszba való beszálláskor kapott ötlete „egyetlen” ötlet volt, amelyet egy pillanat alatt képes volt teljesen felfogni. Még inkább figyelemre méltó meggyőződése az ötlet helyességéről, a későbbi részletes igazolás majdnem feleslegesnek látszott.
Talán megpróbálhatnám ezt összekapcsolni saját hasonló jellegű tapasztalataimmal. Valójában nem tudok olyan esetet felidézni, amikor egy hirtelen jött jó ötlet annyira teljesnek mutatkozott volna, mint Poincaré (vagy a valódi ihlet sok más idézett) példájában. Nálam szükségesnek látszik, hogy (esetleg csak homályosan) gondolkodjam a kéznél lévő problémán – tudatosan, bár lehet, hogy alacsony szinten, értelmem hátterében. Nyugodtan előfordulhat, hogy valamilyen, inkább pihentető tevékenységet folytatok; jó példa a borotválkozás. Esetleg éppen akkor kezdek gondolkodni egy problémán, amelyet egy időre félretettem. A megfontolt, tudatos aktivitás sok kemény órájára biztosan szükség van, és olykor az is eltart egy ideig, amíg újra beledolgozom magam a problémába. De a „felvillanó” ötlet – a helyességéről való meggyőződés erős érzésével együtt – nem ismeretlen számomra.
Érdemes talán elmondani egy további különös érdekességet mutató példát. 1964 őszén a feketelyuk-szingularitások problémáján töprengtem. Oppenheimer és Snyder 1939-ben megmutatták, hogy egy tömeges csillag egzaktul gömbszimmetrikus kollapszusa egy középponti téridő-szingularitáshoz vezet – ami túlmegy az általános relativitáselmélet klasszikus elméletének határain (lásd 7. fejezet). Sok ember úgy érezte, hogy e kellemetlen következtetést elkerülhetik, ha feladják az egzakt gömbszimmetria (ésszerűtlen) feltevését. Gömbszimmetrikus esetben az egész összeomló anyag egyetlen középső pontot vesz célba, ahol, a szimmetria miatt talán nem is váratlanul, egy végtelen sűrűségű szingularitás lép fel. Nem látszott ésszerűtlennek az a feltevés, hogy ilyen szimmetria nélkül az anyag rendezetlenebbül érkezik a középső tartományba, és nem keletkezik végtelen sűrűségű szingularitás. Talán még az is előfordulhat, hogy az egész anyag újra kiörvénylik és így egészen más viselkedést mutat, mint az Oppenheimer–Snyder-féle idealizált fekete lyuk esetében.182
Saját gondolataimat a feketelyuk-probléma iránt mutatkozó megújult érdeklődés ösztönözte, amely a kvazárok egészen új felfedezéséből táplálkozott (a 60-as évek elején). E figyelemre méltóan fényes és távoli csillagászati objektumok fizikai természete sok embert vezetett arra a gondolatra, hogy középpontjukban az Oppenheimer–Snyder-féle fekete lyukakhoz hasonló valami foglalhat helyet. Sokan viszont azt gondolták, hogy a gömbszimmetria feltevése teljesen félrevezető képet nyújthat. Ám nekem az jutott eszembe (egy más összefüggésben végzett munka tapasztalatából), hogy esetleg be lehet bizonyítani egy pontos matematikai tételt, amely szerint a téridő-szingularitások elkerülhetetlenek (a szabványos általános relativitáselmélet szerint), és így a feketelyuk-kép fenntartható – feltéve, hogy a kollapszus elért már egy „pontot, ahonnan nincs visszaút”. Ez utóbbira (gömbszimmetriát nem feltételezve) nem tudtam semmiféle matematikailag definiálható feltételt, a tétel kimondásáról és bizonyításáról nem is beszélve. Egy munkatársam (Ivor Robinson) látogatott meg az USA-ból, és egy egészen más témában nagy beszélgetésbe keveredtünk, amint az utcán sétáltunk munkahelyem, a Birkbeck College felé Londonban. A beszélgetés egy pillanatra megszakadt, amikor átmentünk egy széles úton, de a másik oldalon újra megindult. Nyilvánvalóan az alatt a néhány másodperc alatt támadt egy ötletem, de a folytatódó beszélgetés kitörölte agyamból!
Aznap később, amikor munkatársam már elment, visszatértem az intézetbe. Emlékszem: egészen különös mámorosság érzés fogott el, amelyről nem tudtam számot adni. Végigvettem fejemben mindent, ami aznap történt velem, hogy megtaláljam ennek az érzésnek az okát. Miután számos lehetőséget kizártam, végül visszaidéztem az útkereszteződésnél támadt gondolatomat – amely futólagosan megmámorosított, mert az agyam mélyén őrlődő probléma megoldását adta! Ez volt a szükséges feltétel, amelyet később „csapdafelületnek” neveztem el; aztán már nem tartott sokáig felvázolnom a keresett tétel bizonyítását (Penrose 1965). A teljesen szigorú bizonyítás még így is belekerült némi időbe, de a kulcsot az az ötlet adta, amely az útkereszteződésben jutott eszembe. (Olykor eltűnődöm, mi történt volna, ha aznap valami más, lényegtelen, de örvendetes esemény ért volna. Esetleg soha nem tudtam volna felidézni a csapdafelület gondolatát!)
Ez a történet az ihlet és meglátás egy másik kérdéséhez vezet el, nevezetesen hogy ítéleteink kialakításában rendkívül értékesek az esztétikai követelmények. A művészetekben, mondhatjuk, ezek mindenekfelett állnak. Az esztétika a művészetekben magasröptű téma, voltak filozófusok, akik egész életüket ennek szentelték. Lehet azt mondani, hogy a matematikában és a természettudományokban ezek a feltételek csak esetlegesek, az igazság kritériuma áll mindenekfelett. Ám úgy látszik, hogy amikor az ihlet és meglátás problémáit feszegetjük, lehetetlen elválasztani az egyiket a másiktól. Benyomásom szerint az erősgyőződés a felvillant ihlet érvényességéről (hozzáteszem, nem 100%-osan, de legalábbis a véletlennél sokkal megbízhatóbban) nagyon szoros kapcsolatban áll az esztétikai minőséggel. Egy szép ötletnek sokkal nagyobb esélye van, hogy jó ötlet legyen, mint egy csúnyának. Legalábbis ez az én tapasztalatom, és hasonló érzéseket fejeztek ki mások is (vö. Chandrasekhar 1987). Hadamard (1945, 31. o.) például a következőket írja:
…világos, jelentős felfedezés vagy találmány nem születhet a megtalálás szándéka nélkül. Poincarénál azonban valami mást látunk, a szépérzék belépését, mint a felfedezés nélkülözhetetlen eszközét. Következtetésünk kettős: a felfedezés választás, ezt a választást szükségszerűen a tudományos szépérzék irányítja.
Továbbmenve: Dirac (1982) például rendíthetetlenül állította, hogy a szépség utáni heves vágya tette képessé, hogy megsejtse az elektronra vonatkozó egyenletét (az 5. fejezetben megemlített „Dirac-egyenletet”), míg mások hiába keresték.
Biztonsággal tanúsíthatom az esztétikai minőség fontosságát gondolkodásomban, mind a „meggyőződéssel”, amit az „ihletettnek” minősíthető ötleteknél éreztem, mind a „rutinszerűbb” sejtésekkel kapcsolatban, amelyek folyamatosan jönnek, amint megérezzük az utat a remélt cél felé. Írtam erről máshol, különösen a 10.3. és 4.11. ábrákon látható aperiodikus parkettázások felfedezésével kapcsolatban. Kétségtelen, hogy az első ilyen parkettaminta esztétikai tulajdonságai – nem pont vizuális megjelenése, hanem érdekes matematikai sajátosságai – engedtek utat az intuíciónak (valószínűleg egy „felvillanásban”, de csak kb. 60%-os biztonsággal!), hogy a lefedés megfelelő illesztési szabályokkal kikényszeríthető. Hamarosan többet is mondok még ezekről a parkettamintákról (vö. Penrose 1974).
Számomra világosnak látszik, hogy az esztétikai feltétel fontossága nemcsak az ihlet pillanatszerű ítéleteiben érvényesül, hanem azokban a sokkal gyakoribb ítéletekben, amelyeket a matematikai (vagy természettudományos) munkában állandóan megteszünk. A szigorú bizonyítás rendszerint az utolsó lépés! Előtte sok sejtést kell tenni, és ezeknél az esztétikai meggyőződés rendkívül fontos – mindig korlátozva logikai érvekkel és az ismert tényekkel.
Ezeket az ítéleteket tekintem a tudatos gondolkodás ismertetőjegyének. Sejtésem az, hogy még a meglátás hirtelen felvillanása ellenére is, amelyet a tudatalatti értelem készen állít elő, a tudatosság a döntőbíró, és az ötletet gyorsan elvetnénk és elfelejtenénk, ha „hamisan csengene”. (Én furcsa módon valóban elfelejtettem csapdafelületemet, de ez nem az a szint, amelyre gondolok. Az ötlet elég mélyen behatolt a tudatba ahhoz, hogy ott maradandó benyomást hagyjon.) Az „esztétikai” elvetés, amelyre utalok, feltevésem szerint megakadályozza, hogy a nem vonzó ötletek a tudatosság észrevehetően állandó szintjére jussanak.
Mi hát akkor az álláspontom a tudatalatti szerepéről az ihletett gondolatokban? Elismerem, hogy ezek a kérdések nem annyira világosak, mint amennyire szeretném. Olyan terület ez, ahol a tudatalatti láthatóan nagyon lényeges szerepet játszik, és egyet kell értenem azzal a nézettel, hogy a tudatalatti folyamatok fontosak. El kell ismernem azt is, nem lehetséges, hogy a tudattalan értelem véletlenszerűen veti fel az ötleteket. Kell lennie egy jó hatásfokú válogatási folyamatnak, amely a tudatos értelmet csak olyan gondolatokkal engedi zavarni, amelyeknek „van esélyük”. Azt sugallom, hogy ezeket a kiválasztási feltételeket – nagyban valamiféle „esztétikaiakat” – már erősen befolyásolják a tudatos vágyakozások (mint a csúnyaság érzése, amely olyan matematikai gondolatokkal társul, amelyek nem férnek össze a már lefektetett alapelvekkel.)
Ezzel kapcsolatban felmerül az a kérdés, mi számít igazán eredetinek. Én ennek két tényezőjét látom, egy „felállító” és egy „lelövő” folyamatot. Úgy képzelem, hogy a felállító nagyban tudattalan, a lelövő nagyban tudatos. Hatásos felállító folyamat nélkül egyáltalán nem születnének új ötletek. Önmagában azonban kevés értéke volna ennek az eljárásnak. Szükség van egy hatásos ítéletalkotási eljárásra is, hogy csak az ésszerű eséllyel rendelkező ötletek maradjanak meg. Az álomban például könnyen jöhetnek elő szokatlan gondolatok, ám csak nagyon ritkán élik túl az éber tudatosság kritikai ítéleteit. (Nekem soha nem volt álmomban sikeres tudományos ötletem, mások, mint a kémikus Kekulé a benzol szerkezetének felfedezésében, szerencsésebbek lehetnek.) Véleményem szerint az eredetiség kérdésében a tudatos lelövési (ítélkezési) folyamat a központi fontosságú, sokkal inkább, mint a tudattalan felállító; de tudom, hogy sokan mások ellentétes véleményen lehetnek.
Mielőtt a dolgokat ebben az eléggé nem kielégítő állapotban hagynánk, megemlítem az ihletett gondolkodás egy másik érdekes tulajdonságát, nevezetesen átfogó jellegét. Poincaré története meglepő példával szolgált, mert a gondolat, amely egy röpke pillanatban jutott eszébe, a matematika egy nagy területét fogta át. A nem matematikus Olvasó számára talán közvetlenebb (bár kétségtelenül nem érthetőbb) az, ahogy (egyes) művészek alkotásuk egészét egyszerre képesek fejükben tartani. Elevenen hat Mozart egyik meglepő példája (ahogy Hadamard idézi, 1945):
Amikor jól érzem magam és jókedvű vagyok, vagy amikor egy jó étkezés után kocsikázom vagy sétálok, vagy éjjel, amikor nem tudok aludni, csak úgy özönlenek gondolataim. Honnan jönnek és hogyan? Nem tudom, nem kell hozzá semmit tennem. Amelyek tetszenek, azokat megőrzöm fejemben és zümmögöm magamban; legalábbis mások ezt mondták. Ha a téma már megvan, jön egy másik dallam, hozzákapcsolódik az elsőhöz, összhangban a kompozíció mint egész követelményeivel: az ellenpont, az összes hangszer szólama, minden dallamtöredék végül megteremti a teljes művet. Lelkemet ekkor felgyújtja az ihlet. A mű növekszik; egyre jobban tágul, egyre világosabban értem, míg végül fejemben összeáll a teljes kompozíció, bármilyen hosszú is. Értelmem akkor birtokba veszi, mint ahogy szemem megpillant egy szép képet vagy egy csinos ifjút. A részek nem egymás után jönnek, részletesen kidolgozva, mint ahogy később lesznek, hanem az egész, teljességében, ahogy képzeletem hallani engedi.
Úgy látom, ez összhangban van a dolgok felállító/lelövő rendszerével. A felállítás tudattalannak látszik („nem kell hozzá semmit tennem”), bár kétségtelenül nagyon válogatós, míg a lelövés az ízlés tudatos bírája („amelyek tetszenek, azokat megőrzöm…”). Az ihletett gondolkodás átfogó jellege különösen megfigyelhető a Mozart-idézetben („nem egymás után jönnek …, hanem az egész, teljességében”) és Poincarénál is („A gondolatot nem ellenőriztem; nem lett volna időm rá”). Mi több, azt állítom, hogy tudatos gondolkodásunkban már általánosan figyelemre méltó globalitás van. Hamarosan visszatérek erre a kérdésre.
182 A „fekete lyuk” szakkifejezés csak sokkal később, 1968 körül vált közhasználatúvá (főleg az amerikai fizikus, John A. Wheeler profetikus elképzelései révén).
A gondolkodás nem szóbeli jellege
Hadamard tanulmányában a kreatív gondolkodásról az egyik fő pont meggyőző cáfolata annak az oly sokat hangoztatott tételnek, hogy a szóbeliség szükséges a gondolkodáshoz. Aligha tehetünk jobbat, mint hogy idézünk egy levélből, amelyet Albert Einsteintől kapott ebben a témában:
A szavaknak vagy a nyelvnek, ahogy írunk vagy beszélünk, semmi szerepe nem látszik gondolkodásom mechanizmusában. A fizikai dolgok, amelyek a gondolkodás elemeiként szolgálnak, bizonyos jelek és többé-kevésbé világos képek, amelyek „önkényesen” reprodukálhatók és kombinálhatók… Esetemben az előbb említett elemek vizuális és részben izomi típusúak. A hagyományos szavakat vagy más jeleket csak egy második szakaszban kell fáradsággal megkeresni, amikor az említett kapcsolás már elegendően megalapozott, és kívánságra reprodukálható.
Érdemes idézni Francis Galtont, a kiváló genetikust is:
Az írásban és még inkább a magyarázatban számomra komoly hátrányt jelent, hogy szavakban nem gondolkodom olyan könnyen, mint másképp. Gyakran megtörténik, hogy mikor kemény munka után olyan eredményekhez jutok el, amelyek számomra teljesen világosak és kielégítőek, és megpróbálom azokat nyelvben kifejezni, úgy érzem, hogy először egy egészen más intellektuális síkra kell helyezkednem. Gondolataimat nyelvre kell lefordítanom, amely nem szalad velük nagyon simán. Ezért rengeteg időt vesztegetek el a megfelelő szavak és kifejezések keresgélésével, és amikor hirtelen beszélnem kell, gyakran csupán a szóbeli ügyetlenségek miatt vagyok nagyon homályos, és nem azért, mert nem akarom világosan kifejezni magam. Egyike ez életem kis kellemetlenségeinek.
Hadamard maga így ír:
Állítom, hogy a szavak teljesen hiányoznak fejemből, amikor igazán gondolkodom, és tökéletesen azonosulok Galtonnal abban az értelemben, hogy még egy kérdés elolvasása vagy meghallgatása után is minden szó eltűnik abban a pillanatban, amikor gondolkodni kezdek rajta; és teljesen egyetértek Schopenhauerrel, amikor azt írja, hogy „a gondolatok abban a pillanatban meghalnak, amikor szavakban testesülnek meg”.
Azért idézem ezeket a példákat, mert nagyon összhangban vannak saját gondolkodási szokásaimmal. Majdnem minden matematikai gondolatom vizuális és nem szóbeli fogalmak formájában él, noha a gondolatokat elég gyakran kísérik üres és majdnem haszontalan szóbeli megjegyzések, mint „ez a dolog azzal, az a dolog amazzal jár”. (Használhatok olykor szavakat egyszerű logikai következtetésekre.) Magam is gyakran tapasztalom a nehézségeket, amelyeket gondolataik szavakba öntése ezeknek a gondolkodóknak jelentett. Az ok gyakran az, hogy egyszerűen nincsenek megfelelő szavak a fogalmak kifejezésére. Gyakran számolok például speciálisan tervezett diagramokat használva, amelyek rövidítései bizonyos típusú algebrai kifejezéseknek (vö. Penrose és Rindler 1984, 7. fejezet). Nagyon fáradságos dolog volna ezeket a diagramokat szavakra lefordítani, ezt csak végső megoldásként tenném, ha szükségessé válna, hogy részletes magyarázatot adjak másoknak. Ehhez kapcsolódik az a megfigyelésem, hogy olykor, ha egy ideig erősen összpontosítok a matematikára és hirtelen valaki beszélgetésbe akar vonni, akkor másodpercekig majdnem képtelen vagyok beszélni.
Nem azt mondom, hogy néha nem gondolkodom szavakban, csak azt, hogy a matematikai gondolkodásban a szavakat majdnem haszontalannak találom. Más típusú gondolkodás, mint esetleg a filozofálás, úgy látszik, sokkal jobban alkalmas a szóbeli kifejezésre. Talán ezért az a véleménye oly sok filozófusnak, hogy a nyelv lényeges az intelligens vagy tudatos gondolkodáshoz! Kétségtelen, hogy a különböző emberek nagyon különböző módokon gondolkodnak – még a matematikusok körében is ez a tapasztalatom. A matematikai gondolkodásban a két fő pólusnak az analitikus, illetve a geometriai látszik. Érdekes, hogy Hadamard magát az analitikus oldalon állónak tekintette, noha nem szóbeli, hanem vizuális képeket használt matematikai gondolkodásában. Ami engem illet, én nagyon a dolgok geometriai végénél állok, de a matematikusok spektruma általában nagyon széles.
Ha egyszer elfogadtuk, hogy a tudatos gondolkodás jelentős része lehet nem szóbeli jellegű – szerintem az elmondottakból ez a következtetés elkerülhetetlen –, akkor talán az Olvasó nem is találja olyan nehezen elhihetőnek, hogy az ilyen gondolkodásnak nemalgoritmikus összetevője is lehet!
Emlékezzünk rá, hogy a 9. fejezetben utaltam arra a gyakran hangoztatott nézetre, hogy az agynak csak az a fele képes a tudatosságra, amelyik képes a beszédre (a túlnyomó többségben a bal). Az Olvasó számára az előző fejtegetés fényében világos kell legyen, miért találom ezt a nézetet teljességgel elfogadhatatlannak. Nem tudom, hogy a matematikusok összességükben inkább használják-e agyuk egyik vagy másik oldalát; de nem lehet kétség afelől, hogy az igazi matematikai gondolkodáshoz a tudatosság magas szintjére van szükség. Míg az analitikus gondolkodás főként az agy bal oldali tájain látszik megtörténni, a geometriai gondolkodást gyakran teszik a jobb oldalra, így nagyon ésszerű az a sejtés, hogy a tudatos matematikai tevékenység egy jó része valóban a jobb oldalon zajlik!
Állati tudatosság?
Mielőtt elhagyjuk a tudatosság szóbeliségének területét, rátérek a korábban már felvetett kérdésre, hogy lehetnek-e tudatosak az állatok. Úgy látom, hogy az emberek azt, hogy az állatok nem képesek beszélni, észlelhető tudatosságuk elleni érvként hozzák olykor fel – és ennek velejárójaként az ellen, hogy „jogaik” legyenek. Az Olvasó jól érzékelheti, hogy ezt tarthatatlan gondolatmenetnek tekintem, minthogy nagyon finom tudatos gondolkodás (például a matematikai) folytatható szóbeliség nélkül. Olykor azt is mondják, hogy az agy bal oldala olyan „kevéssé” tudatos, mint egy csimpánz, szintén a szóbeli képességek hiánya miatt (vö. LeDoux, 1985, 4–5. fejezet).
Komoly vita folyik arról, hogy vajon a csimpánzok és gorillák képesek-e valódi szóbeliségre, ha jelbeszédet használhatnak, és nem csak a rendes emberi beszédet (amelyre megfelelő hangszálak hiányában nem képesek). (Lásd Blakemore és Greenfield 1987 változatos cikkeit.) A vita ellenére világosnak látszik, hogy ilyen úton képesek a kommunikációnak legalábbis bizonyos elemi fokára. Véleményem szerint egyes emberek kissé ostoba módon nem engedik ezt „szóbeliségnek” nevezni. Azzal, hogy az emberszabású majmokat kizárják a szóbeliek klubjából, egyesek talán azt remélik, hogy kizárhatják őket a tudatos lények klubjából is!
A beszéd kérdését most félretéve jó bizonyítékok vannak arra, hogy a csimpánzok valódi ihletettségre képesek. Konrad Lorenz (1972) egy szobában lévő csimpánzról ír, a mennyezetről egy banán lóg le, amelyet éppen nem ér el, és van még egy doboz a szobában máshol:
A dolog nem hagyta békén, újra meg újra visszatért hozzá. Aztán előzőleg borús arca – másképp leírni nem lehet – hirtelen „kigyúlt”. Szemei a banánról az alatta lévő üres padlóra váltottak, innen a dobozra, majd vissza az üres területre, és megint a banánra. A következő pillanatban egy örömkiáltást hallatott, majd hamisítatlan jókedvvel a dobozhoz bukfencezett. A sikerben teljesen biztosan tolta a dobozt a banán alá. Aki figyelte, nem vonhatta kétségbe a valódi „aha” élmény meglétét az emberszabású majmoknál.
Megjegyezzük, hogy éppen úgy, ahogy Poincaré az omnibuszra felszálltában, a csimpánz is „teljesen biztos volt sikerében”, mielőtt elképzelését ellenőrizte volna. Ha igazam van, hogy az ilyen ítéletekhez tudatosság kell, akkor itt a bizonyíték, hogy az állatok is lehetnek tudatosak.
Érdekes kérdés merül fel a delfinekkel (és cetekkel) kapcsolatban. Megemlíthetjük, hogy a delfinek nagyagya ugyanolyan nagy (vagy nagyobb), mint a miénk, és hogy rendkívül bonyolult hangjeleket tudnak egymásnak küldeni. Előfordulhat, hogy nagyagyuk az emberi vagy közel emberi skálájútól eltérő „intelligencia”-célokat szolgál. Továbbmenve, fogni tudó kéz hiányában nem képesek olyan típusú „civilizációt” felépíteni, amelyet méltányolnánk – és bár ugyanezen okból könyvet sem képesek írni, olykor filozófusok lehetnek, és tűnődhetnek az élet értelmén, és azon, miért vannak ők! Továbbíthatják-e „tudatosság” érzéseiket a bonyolult víz alatti hangjelek útján? Nincs tudomásom olyan kutatásról, amely jelezné, hogy vajon agyuk meghatározott oldalát használják-e a „szóba öntésre” és az egymással való érintkezésre. Kapcsolódva az embereken végzett „agyhasítási” műtétekhez, amelyek „önmagunk” rejtélyes folytonosságát mutatták, meg kell jegyeznünk, hogy a delfineknek nem alszik egyidejűleg az egész agyuk,183 csak az egyik oldal. Tanulságos volna megkérdezni őket, mit „éreznek” ők a tudatosság folytonosságáról!
183 Nekem úgy tetszik, hogy az a tény, hogy az állatoknak alvásra van szükségük, amelynek során olykor álmodni látszanak (ami kutyáknál gyakran megfigyelhető), bizonyíték arra, hogy tudatosságuk lehet. A tudatosság szempontjából fontos elemnek látszik az álmodó és a nem álmodó alvás megkülönböztetése.
Kapcsolat Platón világával
Említettem, hogy a különböző emberek láthatóan sokféle, egymástól eltérő módon gondolkodnak – még a matematikusok is különbözőképpen gondolkodnak a matematikáról. Visszaemlékszem, hogy amikor az egyetemre kerültem tanulni, azt vártam, hogy a többiek, leendő matematikus kollégáim, többé-kevésbé úgy gondolkodnak, ahogy én. Korábbi iskolai tapasztalatom az volt, hogy osztálytársaim tőlem egészen eltérő módon gondolkodtak, amit némileg zavarónak találtam. „Most”, gondoltam izgatottan, „olyan kollégákat fogok találni, akikkel sokkal könnyebben tudok majd kapcsolatot teremteni! Egyesek termékenyebben gondolkodnak majd nálam, egyesek kevésbé, de mindnyájan azonos hullámhosszon leszünk majd.” Mennyire tévedtem! Azt hiszem, nagyobb gondolkodásmódbeli különbségekkel találkoztam, mint korábban valaha is! A sajátom sokkal inkább geometriai és kevésbé analitikus volt, mint másoké, de sok más különbség is volt kollégáim gondolkodásmódjai között. Mindig különös nehézségekkel küszködtem egy képlet szóbeli leírásának megértésében, míg sok más kollégámnak az ilyesmi láthatóan nem okozott gondot.
Gyakran tapasztaltam, ha valaki megpróbált valamit elmagyarázni nekem a matematikából, hogy bármilyen figyelmesen hallgatom, majdnem teljesen elvesztem a szavak közötti logikai kapcsolatokat. Azonban agyamban kialakult egy megsejtett kép azokról a gondolatokról, amelyekről meggyőzni próbált – teljesen a magam értelmezésében, látszólag nagyon kevés kapcsolattal ahhoz a szellemi képhez, amely kollégám saját felfogásának alapját képezte – és válaszoltam. Meglepetésemre megjegyzéseimet általában mint odaillőket fogadták, és a beszélgetés ezen a módon zajlott. A végére nyilvánvaló volt, hogy valódi, pozitív kommunikáció folyt. Azonban a tényleges mondatokat, amelyeket egyikünk vagy másikunk mondott, csak nagyon ritkán értette meg a másik! Az ezt követő éveimben mint hivatásos matematikus (vagy matematikai fizikus) e jelenséget nem találtam kevésbé igaznak, mint egyetemista koromban. Talán ahogy matematikai tapasztalatom növekedett, valamivel jobban megsejtettem, mit jelent mások magyarázata, és talán kissé könnyebben teszek engedményeket más gondolkodásmódok számára, amikor magam magyarázok valamit. Ám lényegében semmi nem változott.
Gyakran jelentett rejtélyt számomra, hogyan lehetséges egyáltalán a kommunikáció e különös eljárás szerint, most azonban megkockáztatnék egyfajta magyarázatot, mert úgy gondolom, mélyebb jelentősége lehet más felvetett problémáknál. A lényeg az, hogy a matematika átadásánál nem egyszerűen tényeket közlünk. Hogy az (esetleges) állítások egy füzérét az egyik személy átadhassa a másiknak, ahhoz szükséges, hogy az első gondosan mondja ki az állításokat, és a második egyesével felfogja azokat. A matematikában azonban a ténybeli tartalom kicsi. A matematikai állítások szükségszerű igazságok (vagy szükségszerű hamisságok!), és még ha az első matematikus állítása csupán tapogatózás is egy ilyen szükségszerű igazság felé, maga ez az igazság lesz az, amit a második matematikus átvesz, feltéve, hogy helyesen értette azt meg. A második szellemi képei részleteikben különbözhetnek az elsőéitől, különbözhetnek a szóbeli leírások is, ám a lényeges matematikai gondolat utat talált közöttük.
Az ilyen típusú kommunikáció egyáltalán nem volna lehetséges, ha nem állna fenn az a tény, hogy az érdekes vagy mély matematikai igazságok valamennyire el vannak osztva az általános matematikai igazságok között. Ha a közlendő igazság mondjuk a 4897 ∙ 512 = 2 507 264 érdektelen állítás volna, akkor a másodiknak valóban meg kellene értenie az elsőt, hogy a pontos állítás átadódjon. Azonban egy matematikailag érdekes állításnál gyakran elkaphatjuk a fonalat még akkor is, ha a leírás nagyon pontatlan volt.
Paradoxont érezhetünk ebben, mert a matematika olyan tárgykör, ahol a pontosság rendkívül fontos. Az írott anyagokban valóban nagy gondot fordítanak arra, hogy a különféle állítások biztosan pontosak és teljesek legyenek. Azonban egy matematikai gondolat (rendszerint szóbeli) átadásánál az ilyen pontosságnak először olykor gátló hatása lehet, és egy határozatlanabb és inkább leíró formájú közlésre lehet szükség. Ha egyszer a gondolat lényegét felfogtuk, akkor utána már következhetnek a részletek.
Hogyan lehet az, hogy a matematikai gondolatok közölhetők ezen a módon? Úgy képzelem, hogy valahányszor az értelem felfog egy matematikai gondolatot, kapcsolatba lép a matematikai fogalmak platóni világával. (Emlékezzünk vissza, hogy a platóni nézőpont szerint a matematikai gondolatok önmagukban léteznek, egy ideális platóni világot népesítenek be, amely csak az értelem útján érhető el; vö. 3. és 5. fejezet.) Amikor valaki „lát” egy matematikai igazságot, akkor tudata betör ebbe a gondolatvilágba, és („az értelem útján”) közvetlen kapcsolatot teremt vele. Ezt a „látást” a Gödel-tétellel kapcsolatban írtam le, de minden matematikai megértésnek ez a lényege. A matematikusok érintkezése azáltal válik lehetővé, hogy mindegyiknek van egy közvetlen útja az igazsághoz, tudatosságuk olyan helyzetben van, hogy a matematikai igazságokat e „látás” folyamatán keresztül közvetlenül érzékeli. (Az érzékelésnek ez a művelete valóban gyakran társul az „Ó, látom” szavakkal!) Minthogy mindegyikük közvetlen kapcsolatot képes teremteni a platóni világgal, könnyebben tudnak egymással kommunikálni, mint azt várni lehetne. A szellemi képek, amelyekkel rendelkeznek, mikor létrehozzák e platóni kapcsolatot, egészen különbözőek lehetnek, de a kommunikáció lehetséges, mert mindnyájan közvetlen kapcsolatban állnak ugyanazzal a külsőleg létező platóni világgal!
E nézet szerint az értelem mindig képes e közvetlen kapcsolatra. De egyszerre csak kevés jöhet át. A matematikai felfedezés során az érintkezési terület kiszélesedik. Minthogy a matematikai igazságok szükségszerű igazságok, a felfedező tényleges „információt” technikai értelemben nem kap. Minden információ ott van az egész idő alatt. Csak össze kell a dolgokat hozni és „látni” a választ! Ez nagyon összevág Platón saját elképzelésével, hogy (mondjuk a matematikai) felfedezés csak az emlékezés egy formája! Valóban gyakran megütődöm a hasonlóságon, mikor nem vagyok képes emlékezni valakinek a nevére, és mikor nem tudom megtalálni a helyes matematikai fogalmat. A keresett fogalom mindkét esetben egyfajta értelemben már jelen van az értelemben, bár ez kevésbé szokásos szóhasználat egy felfedezetlen matematikai gondolat esetében.
Hogy a dolgok ilyen szemlélete hasznos legyen a matematikai kommunikáció esetében, úgy kell képzelnünk, hogy az érdekes és mély matematikai gondolatok valahogyan erősebben léteznek, mint az érdektelenek vagy triviálisak. Ennek jelentősége lesz a következő szakasz spekulatív fejtegetéseiben.
Egy nézet a fizikai valóságról
Minden teóriának arról, hogyan jön létre a tudatosság a fizikai valóság világán belül, legalább hallgatólagosan foglalkoznia kell magának a fizikai valóságnak kérdésével.
Az EMI nézőpontja például azt állítja, hogy az „értelem” egy elegendően összetett algoritmus megtestesülésén keresztül találja meg létezését, amint a fizikai világ objektumai kiváltják ezt az algoritmust. A feltevés szerint nem számít, mik ezek a tényleges objektumok. Idegi jelek, huzalokban folyó elektromos áramok, kerékfogak, csigák vagy vízcsövek egyformán lehetnek. Magát az algoritmust tekintik nagyon fontosnak. De hogy egy algoritmus minden különös fizikai megtestesüléstől függetlenül „létezzen”, ahhoz a matematika egy platóni nézőpontja látszik szükségesnek. Egy EMI-pártoló nehezen választhatná azt az alternatívát, hogy „a matematikai fogalmak csak az értelemben léteznek”, mert a kör bezárulna, előzetesen létező értelem kellene az algoritmus létezéséhez és előzetesen létező algoritmus az értelemhez! Próbálkozhatnak azzal a vonallal, hogy az algoritmusok létezhetnek mint jelek egy papírdarabon vagy mágnesezettségi irányok egy vastömbben vagy töltésátrendeződések egy számítógép memóriájában. Azonban az anyag ilyen elrendezései önmagukban nem alkotnak algoritmust. Hogy azzá váljanak, értelmezésre van szükség, azaz hogy lehetséges legyen megfejteni az elrendezéseket; ez pedig függ attól a „nyelvtől”, amelyen az algoritmus íródott. Megint egy előzetesen létező értelemre van szükség, hogy „megértse” a nyelvet, visszakerültünk ugyanoda, ahol voltunk. Elfogadva hát, hogy algoritmusok népesítik be Platón világát és így az EMI-nézet szerint az a világ az, ahol az értelem keresendő, szembekerülünk a kérdéssel, mi a viszonya egymáshoz a fizikai világnak és a platóni világnak. Én úgy látom, ez az értelem–test probléma EMI-változata!
Az én nézőpontom különbözik ettől, mert azt hiszem, hogy a (tudatos) értelem nem algoritmikus. Ám némileg zavartan veszem észre, hogy elég sok közös pont van az EMI-nézőpont és a sajátom között. Jeleztem, hogy úgy vélem, a tudatosság közeli kapcsolatban áll a szükségszerű igazságok érzékelésével – és ezáltal a matematikai fogalmak platóni világával való közvetlen kapcsolat létrehozásával. Ez nem algoritmikus eljárás – és nem az e világot esetleg benépesítő algoritmusok azok, amelyek különösen érdekelnek bennünket –, ám az értelem–test probléma e nézet szerint megint igen szorosan látszik kapcsolódni a kérdéshez, mi a viszonya Platón világának a tényleges fizikai objektumok „valóságos” világához.
Az 5. és 6. fejezetben láttuk, milyen figyelemre méltó összhangban van a valóságos fizikai világ nagyon pontos matematikai rendszerekkel (a SZUPER elméletekkel). Gyakran hangsúlyozzák, valóban mennyire rendkívüli ez a pontosság (vö. különösen Wigner 1960). Nehéz elhinnem, amit egyesek állítanak, hogy ezek a SZUPER elméletek csupán a gondolatok véletlenszerű természetes kiválasztódása által keletkeztek, amelyben csak a jók maradtak meg. A jók túlságosan jók ahhoz, hogy a véletlenszerűen felmerülő elképzelések közül egyszerű túlélők legyenek. Kell valamilyen mély oka legyen a matematika és fizika, azaz a platóni világ és a fizikai világ közötti összhangnak.
Hogy a „platóni világról” egyáltalán beszélünk, az azt jelenti, hogy valamiféle valóságot tulajdonítunk neki, amely valamely módon összehasonlítható a fizikai világ valóságával. Másrészt a fizikai világ valósága maga sokkal ködösebbnek látszik, mint látszott régebben, a relativitáselmélet és a kvantummechanika SZUPER elméletek eljövetele előtt (lásd az 5. és a 6. fejezetet). Ezen elméletek pontossága egy majdnem absztrakt matematikai létezést kínált a tényleges fizikai valóság számára. Paradoxon-e ez? Hogyan válhat a konkrét valóság absztrakttá és matematikaivá? Ez talán az érem másik oldala abban a kérdésben, hogy az absztrakt matematikai fogalmak hogyan kaphatnak majdnem konkrét valóságot Platón világában. Lehet, hogy valamilyen értelemben a két világ ténylegesen ugyanaz? (Vö. Wigner 1960; Penrose 1979a; Barrow 1988; valamint Atkins 1987.)
Bár erősen rokonszenvezek e két világ tényleges azonosításának e gondolatával, a kérdés nem csak ennyiből áll. Amint azt a 3. fejezetben és korábban ebben a fejezetben említettem, bizonyos matematikai igazságoknak, úgy látszik, erősebb („mélyebb”, „érdekesebb”, „termékenyebb”?) a platóni valósága, mint másoknak. Ezek volnának azok, amelyek erősebben azonosítandók a fizikai valósággal. (Egy ilyen dolog volna a komplex számok rendszere (vö. 3. fejezet), lévén alapvető tartozéka a kvantummechanikának, a valószínűségi amplitúdóknak.) Ez az azonosítás érthetőbbé tenné, hogyan valósíthat meg az „értelem” rejtélyes kapcsolatokat a fizikai világ és a matematika platóni világa között. Emlékezzünk arra is, a 4. fejezetben volt róla szó, hogy a matematikai világnak sok olyan része van – mi több, a legmélyebb és legérdekesebb részei –, amelyek nemalgoritmikus jellegűek. A kifejteni igyekezett nézőpont alapján ezért valószínűnek látszik, hogy a fizikai világon belül nagyon jelentős szerepet kell kapjon a nemalgoritmikus működés. Azt sugallom, hogy ez a szerep szorosan kötődik magához az „értelem” fogalmához.
Determinizmus és erős determinizmus
Mindeddig keveset mondtam a „szabad akarat” kérdéséről, amelyet általában az értelem–test probléma aktív része alapkérdésének tartanak. Ehelyett inkább saját javaslatomra összpontosítottam, mely szerint a tudatos tevékenység szerepének van egy lényeges nemalgoritmikus vonása. A szabad akarat kérdését rendszerint a fizikai determinizmussal összefüggésben tárgyalják. Emlékezzünk arra, hogy a legtöbb SZUPER elméletünkben világos a determinizmus olyan értelemben, hogy ha a rendszer állapota tetszőleges időpillanatban ismert,184 akkor az elmélet egyenletei tökéletesen meghatározzák azt minden későbbi (vagy korábbi) időpontban. Nem látszik tehát hely a „szabad akarat” számára, mert egy rendszer jövőbeli viselkedését a fizikai törvények, úgy látszik, teljesen meghatározzák. Még a kvantummechanika U részének is megvan ez a teljesen determinisztikus jellege. Az R „kvantumugrás” rész azonban nem determinisztikus, és egy teljesen véletlenszerű elemet vezet be az időfejlődésbe. Korábban sokan hangoztatták, hogy itt lehet szerepe a szabad akaratnak, a tudatosságnak esetleg közvetlen hatása lehet arra, ahogy egy kvantumos rendszer ugorhat. Ám ha R igazán véletlenszerű, akkor nem sokat segít, ha valami pozitívat akarunk tenni szabad akaratunkkal.
Az én nézőpontom az, bár ebben a vonatkozásban nincs nagyon jól megfogalmazva, hogy a kvantumos–klasszikus határvonalon egy új eljárás (KKG; vö. 8. fejezet) lép be, amely áthidal U és R között (most mindkettőt közelítésnek tekintjük), és ez az új eljárás egy lényegesen nemalgoritmikus elemet tartalmaz. Ez azzal járna, hogy a jövő nem volna kiszámítható a jelenből, még ha utóbbi determinálhatná is azt. Az 5. fejezetbeli okfejtésemben megpróbáltam világosan szétválasztani a kiszámíthatóság kérdését a determinizmusétól. Nekem egészen elfogadhatónak látszik, hogy a KKG determinisztikus, de nemkiszámítható elmélet lehet.185 (Emlékezzünk vissza a nemkiszámítható „játékmodellre”, amelyet az 5. fejezetben írtam le.)
Az emberek olykor arra az álláspontra helyezkednek, hogy még a klasszikus (vagy U-kvantumos) determinizmus sem hatásos determinizmus, mert a kezdeti feltételeket soha nem ismerhetjük eléggé jól ahhoz, hogy a jövőt ténylegesen számítani tudjuk. Olykor nagyon kis változások a kezdeti feltételekben nagyon nagy különbségekhez vezethetnek a végső eredményben. Ez történik például a „káosz” néven ismert jelenségben egy (klasszikus) determinisztikus rendszerben – példa az időjárási jóslatok bizonytalansága. Nagyon nehéz azonban elhinni, hogy ez a fajta klasszikus bizonytalanság nyit utat szabad akaratunknak (vagy illúziójának?). A jövőbeli viselkedés még így is meghatározott volna egészen az ősrobbanástól, noha képtelenek volnánk azt kiszámítani (vö. 5. fejezet).
Ugyanez az ellenvetés merülhet fel azon javaslatom ellen, hogy a kiszámíthatóság hiánya a dinamikai törvényeknek lehet belső lényege – feltéve most, hogy azok nemalgoritmikus jellegűek – és nem a kezdeti feltételekre vonatkozó információnk hiányának. E nézet szerint a jövő, noha nem kiszámítható, a múlt által teljesen rögzített volna – egészen a Nagy Robbanásig visszamenően. Valójában nem ragaszkodom dogmatikusan ahhoz, hogy a KKG determinisztikus, de nemkiszámítható legyen. Sejtésem szerint a keresett elméletnek ennél finomabb leírása volna. Csupán azt mondom, hogy tartalmaznia kell lényeges, nemalgoritmikus elemeket. E szakasz lezárásaként szeretnék megemlíteni egy, a determinizmus kérdésére vonatkozó, még szélsőségesebb nézetet. Ez az, amire erős determinizmus néven hivatkoztam (Penrose 1987a). Eszerint nem csupán arról van szó, hogy a múlt meghatározza a jövőt; a világegyetem teljes története minden időre rögzített valamilyen pontos matematikai rendszer szerint. E nézőpont vonzó lehet, ha hajlunk arra, hogy a platóni világot azonosítsuk valahogyan a fizikai világgal, mert Platón világa egyszer s mindenkorra rögzített, és a világegyetem számára nincsenek „alternatív lehetőségek”! [Néha kíváncsi volnék, járt-e Einstein fejében egy ilyen rendszer, amikor ezeket írta: „Arra vagyok igazán kíváncsi, vajon megalkothatta volna-e Isten másképp is a világot; azaz, hogy a logikai egyszerűség szüksége hagy-e egyáltalán bármilyen szabadságot!” (Levél Ernst Strausshoz; lásd Kuznyecov 1977, 5. fejezet.)]
Az erős determinizmus egyik változata lehet a kvantummechanika sokvilág-elképzelése (vö. 6. fejezet). Eszerint az a pontos matematikai rendszer nem egyetlen világegyetem-történetet rögzítene, hanem a „lehetséges” világegyetem-történetek miriádjainak összességét. Egy ilyen rendszert (legalábbis számomra) kellemetlen természete és a problémák és elégtelenségek megsokszorozása ellenére nem lehet kizárni mint lehetőséget.
Nekem úgy tetszik, hogy ha van erős determinizmus, de sok világ nélkül, akkor a világegyetem szerkezetét szabályozó matematikai rendszernek valószínűen nemalgoritmikusnak kellene lennie.186 Másképpen elvileg kiszámíthatnánk, mit fogunk csinálni a következőkben, és akkor „elhatározhatnánk” valami egészen mást, ami ellentmondás volna a „szabad akarat” és az elmélet erős determinizmusa között. A nemkiszámíthatóság bevezetésével elkerülhető ez az ellentmondás – bár meg kell vallanom, hogy az ilyen jellegű megoldás némiképp zavar, és valami sokkal finomabbat képzelek el a világ működését irányító tényleges szabályokra!
184 A speciális vagy az általános relativitáselméletben az „idők” helyett „egyidejű tereket” vagy „térszerű felületeket” kell mondani (5. fejezet).
185 Rá lehet mutatni arra, hogy a kvantumgravitációnak van legalább egy olyan megközelítése, amely a nemkiszámíthatóság egy elemét látszik tartalmazni (Geroch és Hartle 1987).
186 A térben végtelen világegyetem esetében azonban van egy kibúvó, minthogy ott (a sokvilág-elmélethez hasonlóan) végtelen sok másolata volna önmagunknak és közvetlen környezetünknek! Az egyes másolatok jövőbeli viselkedései kissé különbözhetnek, és soha nem volnánk egészen bizonyosak, hogy matematikailag modellezett közelítő másolatainknak ténylegesen melyike „lehetnénk”!
Az emberszabású elv
Mennyire fontos a tudatosság a világegyetem egésze számára? Létezhet-e egy világegyetem tudatos lakosok nélkül? Speciálisan tervezettek-e a fizika törvényei, hogy megengedjék a tudatos élet létezését? Van-e valami speciális a világegyetemben elfoglalt helyzetünkben akár térben, akár időben? Ilyen kérdéseket vet fel az emberszabású elv néven ismert elmélet.
Az elvnek sok formája van (lásd Barrow és Tipler 1986). Ezek közül a legtisztábban elfogadható csupán a tudatos (vagy „intelligens”) életnek a világegyetemben elfoglalt térbeli-időbeli helyzetét veti fel. Ez a gyenge emberszabású elv. Érvelésével megmagyarázható, miért alkalmasak a feltételek az (intelligens) élet létezésére a Földön, éppen a jelenlegi időben. Mert ha nem volnának azok, akkor nem itt és most találnánk magunkat, hanem valahol máshol, más megfelelő időben. Ezt az elvet nagyon erőteljesen használta fel Brandon Carter és Robert Dicke egy kérdés megoldásában, amely jó sok évig zavarta a fizikusokat. Megfigyeltek ugyanis változatos és meglepő numerikus összefüggéseket a fizikai állandók (a gravitációs állandó, a proton tömege, az univerzum kora stb.) között. Az volt ennek a rejtélyes oldala, hogy az összefüggések némelyike csak a Föld történetének mai korában áll fenn, tehát úgy látszik, hogy véletlenül egy nagyon speciális időben élünk (néhány millió év ide vagy oda!). Ezt magyarázta később Carter és Dicke azzal, hogy ez a kor egybeesik az ún. fősorozatbeli csillagok, mint a Nap, életkorával. Bármilyen más korban, folytatódik az érvelés, nem volna intelligens élet, hogy megmérje a szóban forgó fizikai állandókat – ezért az egybeesésnek fenn kellett állnia egyszerűen azért, mert intelligens élet csak abban a speciális időben lehet, amikor az egybeesés fennáll!
Az erős emberszabású elv tovább megy. Nemcsak ebben a világegyetemben, hanem a lehetséges világegyetemek végtelen halmazán belül elfoglalt térbeli-időbeli helyzetünkkel foglalkozik. Most már javasolhatunk válaszokat azokra a kérdésekre, hogy a fizikai állandók vagy általában a fizika törvényei miért vannak speciálisan úgy tervezve, hogy létezhet egyáltalán intelligens élet. Az érvelés az, hogy ha az állandók vagy a törvények kicsit is mások volnának, akkor nem ebben a speciális univerzumban élnénk, hanem valamelyik másikban! Véleményem szerint az erős emberszabású elv némileg kétes jellegű, és az elméletiek akkor hajlamosak feléleszteni, amikor nincs elég jó elméletük a megfigyelt tények magyarázatára (például a részecskefizikai elméletekben, ahol a részecskék tömegei nem magyarázhatók, és az érvelés az, hogy ha más értékük volna, mint a megfigyelt, akkor az élet feltehetően nem volna lehetséges stb.) A gyenge emberszabású elv viszont nekem kifogástalannak látszik, feltéve, hogy nagyon óvatosan használják.
Az emberszabású elv használatával – akár az erős, akár a gyenge változattal – meg lehet próbálni megmutatni, hogy a tudatosság elkerülhetetlen annak a ténynek következtében, hogy a világ megfigyeléséhez olyan felfogni képes lényekre van szükség, mint „mi” vagyunk, ezért nem szükséges feltételezni, mint tettem én, hogy a felfogóképesség kiválasztódási előny! Véleményem szerint az érvelés technikailag helyes, és a gyenge emberszabású elv (legalábbis) okot szolgáltathat arra, hogy van tudatosság anélkül, hogy a természetes kiválasztódásnak előnyben kellene azt részesítenie. Másrészt viszont nem tudom elhinni, hogy az emberszabású elv érvelése az igazi (vagy az egyetlen) oka a tudat kifejlődésének. Elég bizonyíték van más irányokból, amelyek meggyőznek, hogy a tudatosság erőteljes kiválasztódási előny, és nem hiszem, hogy az emberszabású érvelésre szükség van.
1./
Másrészt viszont nem tudom elhinni, hogy az emberszabású elv érvelése az igazi (vagy az egyetlen) oka a tudat kifejlődésének. Elég bizonyíték van más irányokból, amelyek meggyőznek, hogy a tudatosság erőteljes kiválasztódási előny, és nem hiszem, hogy az emberszabású érvelésre szükség van.
Parkettázások és kvázikristályok
Eltávolodom most az utolsó néhány szakasz átfogó spekulációitól, inkább egy olyan kérdést vizsgálok, amely, bár még némileg spekulatív, sokkal tudományosabb és „kézzelfoghatóbb”. Először a tárgyhoz nem tartozó kalandozásnak látszik majd, azonban jelentősége számunkra a következő szakaszban világossá válik.
Emlékezzünk vissza a 4.12. ábrán látható parkettázási mintákra. Ezek a minták némiképp figyelemre méltóak a tekintetben, hogy „majdnem” megsértenek egy, a kristályrácsokra vonatkozó, jól ismert matematikai tételt. A tétel azt mondja ki, hogy egy kristályminta számára csak a két-, három-, négy- és hatfogású forgási szimmetria megengedett. Kristálymintán pontok egy diszkrét rendszerét értem, amely eltolási szimmetriával rendelkezik; azaz a mintát el lehet csúsztatni forgatás nélkül úgy, hogy önmagába megy át (azaz e speciális mozgás során nem változik), és ezért van periódus-paralelogrammája (vö. 4.8. ábra). A megengedett forgási szimmetriákkal rendelkező parkettázási mintákra a 10.2. ábrán láthatunk példákat. Na már most, a 4.12. ábra mintái, egy hasonló a 10.3. ábrán látható (amely lényegében a 4.11. ábra parkettáinak összeillesztésével jön létre), viszont majdnem rendelkeznek eltolási szimmetriával, és majdnem van ötfogású szimmetriájuk – ahol a „majdnem” azt jelenti, hogy található a mintának olyan mozgatása (rendre eltolás, illetve forgatás), amely során a minta önmagába megy át előre megadott, a 100%-osnál tetszőlegesen kisebb mértékben. Az állítás pontos jelentésével most nem kell törődnünk. Számunkra egyedül az lesz lényeges, hogy ha volna olyan anyag, amelyben az atomok a minta csúcsainak megfelelően rendeződnének el, akkor ez kristálynak látszana, mégis mutatná a tiltott ötfogású szimmetriát!
1984 decemberében Dany Shechtman izraeli fizikus, aki munkatársaival az USA Nemzeti Szabványügyi Hivatalában, Washingtonban dolgozott, bejelentette, hogy felfedezték egy alumínium-mangán ötvözet egy fázisát, amely valóban kristályszerű anyagnak látszott – most kvázikristálynak hívják – ötfogású szimmetriával. Ez a kvázikristályos anyag valójában három dimenzióban is szimmetriát mutatott, nem csak a síkban – összességében egy tiltott „ikozaéderes” szimmetriát (Shechtman és mások 1984). (Ötfogású sík parkettázásaim háromdimenziós, „ikozaéderes” analogonjait találta meg Robert Ammann 1975-ben, lásd Gardner 1989.) Shechtman ötvözetei csak parányi, kb. 10–3 milliméter vastagságú, mikroszkopikus kvázikristályokat alkottak, ám később más kvázikristályos anyagokat találtak: különösen érdekes volt egy alumínium-lítium-réz ötvözet, amelyben az ikozaéderes szimmetriájú egységek milliméteres nagyságúra is megnőhetnek, és puszta szemmel is egészen jól láthatók (lásd 10.4. ábra).
Az általam leírt kvázikristályos parkettázási minták figyelemre méltó tulajdonsága, hogy felépítésük szükségszerűen nemlokális. Azaz a minták összeállításánál időről időre meg kell vizsgálnunk a minta állapotát az építési ponttól sok-sok „atomnyi” távolságban, ha biztosak akarunk lenni abban, hogy a darabok összerakásánál nem követtünk el komoly hibát. (Ez talán hasonlít a nyilvánvalóan „intelligens tapogatózáshoz”, amelyre a természetes kiválasztódással kapcsolatban utaltam.) Ez a tulajdonság egyik pontja annak a jelentős vitának, amely a kvázikristályos szerkezet és növekedése körül jelenleg folyik, és nem volna okos dolog határozott következtetéseket levonni addig, amíg meg nem oldódik néhány elintézetlen probléma. Spekulálni azonban lehet; megkockáztatom saját véleményem kifejtését. Először is azt hiszem, hogy e kvázikristályos anyagok némelyike valóban magasan szervezett, atomi elrendezéseik igen közel állnak a parkettázási minták szerkezetéhez, amelyekről szó volt. Másodszor, az a (kevésbé határozott) véleményem, hogy nem lehet ezeket ésszerűen összerakni úgy, hogy lokálisan adogatunk hozzájuk atomokat, egyszerre egyet, a kristálynövesztés klasszikus képével összhangban, hanem felépítésüknek kell legyen egy nemlokális, lényegesen kvantummechanikai alkotórésze.187
E növekedésről az én képem a következő: az atomok nem egyesével jönnek és kapcsolódnak egy folytonosan mozgó növekedési vonal mentén (klasszikus kristálynövekedés), hanem a kapcsolódó atomok sok különböző alternatív elrendeződésének egy fejlődő kvantumos lineáris szuperpozícióját kell tekintenünk (amelyet a kvantumos U eljárás szabályoz). A kvantummechanika szerint (majdnem mindig) ennek kell bekövetkeznie! Nem egy dolog történik; sok alternatív atomi elrendeződésnek kell egy komplex lineáris szuperpozícióban együtt élnie. E szuperponált lehetőségek közül néhány sokkal nagyobb konglomerátumokig nő, és az egyes alternatívák gravitációs mezői közötti különbségek egy bizonyos ponton elérik az egygraviton-szintet (vagy valami megfelelőt; lásd 8. fejezet). Ebben a szakaszban az egyik alternatív elrendeződés – vagy, valószínűbben, még mindig egy szuperpozíció, de valamennyire már redukált szuperpozíció – kiválasztódik mint a „tényleges” elrendeződés (az R kvantumos eljárás szerint). E szuperponált építkezés, a határozottabb elrendezések felé vezető redukciókkal együtt, folytatódik az egyre nagyobb skálák felé, míg végül kialakul egy ésszerű méretű kvázikristály.
Általában, amikor a Természet a kristályos alakzatok között keresgél, a legalacsonyabb energiájú alakzat után kutat (ha a háttérhőmérséklet zérus). Hasonlóan képzelem a kvázikristályok növekedését, a különbség annyi, hogy ezt a legalacsonyabb energiájú állapotot sokkal nehezebb megtalálni, és az atomok „legjobb” elrendezését nem lehet úgy felfedezni, hogy egyesével adogatjuk az atomokat abban a reményben, hogy minden egyes atom megoldja a saját minimalizálási problémáját. Helyette egy globális problémát kell megoldanunk. Kooperatív erőfeszítés kell legyen nagyszámú atom között egy időben. Az ilyen együttműködés, állítom, kvantummechanikailag érhető el; úgy, hogy az atomok sok különböző elrendezése egy lineáris szuperpozícióban egyidejűleg kerül „kipróbálásra” (talán némileg hasonlóan a 9. fejezet végén említett kvantumszámítógéphez). A minimumprobléma egy alkalmas (bár valószínűleg nem a legjobb) megoldásának kiválasztása akkor kell megtörténjen, amikor az egygraviton- (vagy egy alkalmas alternatív) feltétel teljesül – ami feltehetően csak akkor következik be, amikor a fizikai feltételek éppen megfelelőek.
187 Még egyes tényleges kristályok növekedése is felvethet hasonló problémákat, például amelyeknél az elemi cella néhány száz atomot tartalmaz, ami az ún. Frank–Casper-fázisokban fordul elő. Másrészt meg kell említenünk, hogy az ötfogású szimmetriával rendelkező kvázikristályokra egy elméleti, „majdnem lokális” (bár még nem lokális) növekedési mechanizmust javasolt Onoda, DiVicenzo, Steinhardt és Socolar (1988).
Egy lehetséges kapcsolat az agy alakíthatóságával
Folytatom tovább ezeket a spekulációkat, és azt kérdezem, lehet e jelentőségük az agy működésének kérdésében. Amennyire látom, a legkínálkozóbb lehetőség az agy alakíthatóságának jelensége. Emlékezzünk vissza, hogy az agy nem teljesen olyan, mint egy számítógép, inkább egy folyamatosan változó számítógéphez hasonlíthatna. E változásokat láthatóan az okozza, hogy a kinövő vagy visszahúzódó dendrittüskéken szinapszisok keletkeznek vagy szűnnek meg (lásd 9. fejezet; 9.15. ábra). Megkockáztatom azt a gondolatot, hogy ezt a növekedést vagy összehúzódást valami hasonló szabályozhatja, mint a kvázikristályok növekedésének folyamatait. Tehát nem csak egy lehetséges alternatív elrendezés kerül kipróbálásra, hanem hatalmas számú, amely mind tagja egy komplex lineáris szuperpozíciónak. Amíg ezen alternatívák hatásai az egygraviton- (vagy valami más) szint alatt maradnak, addig valóban együtt élnek (és az U-kvantummechanika szabályai szerint majdnem változatlanul kell együtt élniük). E szint alatt egyidejű, szuperponált számítások kezdődhetnek, tökéletes összhangban a kvantumszámítógép elveivel. Valószínűtlennek látszik azonban, hogy e szuperpozíciók hosszasan fennmaradjanak, minthogy az idegi jelek elektromos mezőket hoznak létre, amelyek lényegesen megzavarják a környező anyagot (bár a myelinhüvelyek segíthetnek a szigetelésben). Tegyük fel, hogy a számítások ilyen szuperpozíciói legalább annyi ideig fennmaradhatnak, amíg ténylegesen kiszámítanak valami lényegeset, mielőtt elérnék az egygraviton- (vagy akármilyen) szintet. Egy ilyen számítás sikeres eredménye olyan „cél” volna, mint a kvázikristály-növekedés egyszerű energiaminimalizáló „célja”. E „cél” elérése tehát a kvázikristály sikeres növekedéséhez hasonlít!
Nyilvánvalóan sok a homály és a kétség e spekulációkban, de azt hiszem, az analógia igazán tetszetős. Egy kristály vagy kvázikristály növekedését erősen befolyásolják a környezetben lévő megfelelő atomok és ionok koncentrációi. Hasonlóképpen azt lehet jósolni, hogy a dendrittüske-családok növekedését vagy összehúzódását ugyanolyan erősen befolyásolják a környező különféle neurotranszmitter anyagok koncentrációi (kiválthatnak ilyeneket például az érzelmek). Akármelyik atomi elrendeződés is valósul meg (vagy „redukálódik” le), végül mint a tényleges kvázikristály, mind kapcsolatban áll az energiaminimum-probléma megoldásával. Hasonlóképpen, így okoskodom, az agyban ébredő gondolatok is megoldásai valamilyen, de most nem feltétlenül energiaminimum-problémának. Ez a cél általában sokkal bonyolultabb természetű, vannak benne vágyak és szándékok, amelyek maguk is kapcsolódnak az agy számítási oldalaihoz és képességeihez. Úgy okoskodom, hogy a tudatos gondolkodás nagyon szorosan kötődik az előzőleg lineáris szuperpozícióban lévő alternatívák kiválasztásához. Ez mind ahhoz az ismeretlen fizikához tartozik, amely az U és R közötti határterületet szabályozza, és amely, várakozásom szerint, a kvantumgravitáció még fel nem fedezett elméletén – a KKG-n – alapszik!
Lehet-e az ilyen fizikai működés nemalgoritmikus természetű? Emlékezzünk vissza, hogy a 4. fejezetben leírt, általános parkettázási problémának nincs algoritmikus megoldása. Azt lehet jósolni, hogy az atomok építkezési problémái osztozhatnak e nemalgoritmikus tulajdonságban. Ha ezek a problémák elvileg „megoldhatók” azokkal az eszközökkel, amelyekre utaltam, akkor valóban van lehetőség arra, hogy az általam elképzelt típusú agyműködésnek legyen nemalgoritmikus összetevője. Azonban, hogy ez így legyen, ahhoz kell valami nemalgoritmikusnak lennie a KKG-ben. világos, hogy mindez jócskán spekuláció. Ám az előhozott érveket szemlélve úgy látom, határozottan szükség van valamire, ami nemalgoritmikus jellegű.
Milyen gyorsan mehetnek végbe e változások az agykapcsolatokban? Az idegélettannal foglalkozók között némiképp vitatott ez a kérdés, de minthogy az állandó memória a másodperc töredéke alatt eltárolható, ezért elfogadható, hogy a kapcsolatok változásai is ilyen időtartamok alatt mehetnek végbe. Hogy elképzeléseimnek legyen valami esélyük, ahhoz valóban szükséges ez a sebesség.
A tudatosság időkésései
A következőkben elmondok két, embereken végzett kísérletet (Harth 1982), amelyeknek igen figyelemreméltó következményei látszanak mondandónk szempontjából. Arra az időre vonatkoznak, amely alatt a tudatosság működésbe lép. Az első a tudatosság aktív szerepével, a második a passzívval foglalkozik. A következtetések összevetve még meglepőbbek.
Az első kísérletet H. H. Kornhuber és munkatársai végezték Németországban 1976-ban (Deecke, Grötzinger és Kornhuber 1976). Önként vállalkozók fejének egy pontján feljegyezték az elektromos jeleket (EEG, azaz elektroenkefalogram), és azt kérték tőlük, hogy teljesen maguk által választott különböző időpontokban hirtelen hajlítsák be jobb kezük mutatóujját. Az elképzelés az volt, hogy az EEG-adatok jeleznek valamit a koponyában zajló szellemi tevékenységből, az ujj behajlításának tudatos elhatározásából. Hogy az EEG-adatokból határozott jelet kapjanak, az adatokat különböző méréssorozatokra átlagolni kell, az így kapott eredő nem nagyon különleges. Ám amit találtak, az figyelemre méltó, nevezetesen hogy az észlelt elektromos potenciál egy teljes másodperccel – sőt esetleg egy és egy féllel – korábban fokozatosan épül fel, mint mielőtt az ujj ténylegesen begörbül. Ez azt jelzi, hogy a tudatos elhatározás folyamatának egy másodpercre van szüksége, hogy működésbe lépjen! Ez szembeállítható azzal a sokkal rövidebb idővel, amelyre egy külső jelre adott válaszhoz szükség van, ha a válasz módja előzetesen rögzített. Például „szabad akarat” helyett az ujj behajlítása lehet egy fényjel felvillanására adott válasz. Ebben az esetben kb. egyötöd másodperc a normális reakcióidő, amely kb. ötször gyorsabb, mint a Kornhuber által vizsgált „akarati” cselekvés (lásd 10.5. ábra).
A második kísérletben Benjamin Libet a Kalifornia Egyetemről és Bertram Feinstein a San Franciscóban lévő Mount Zion Neurológiai Intézetből (Libet és mások 1979) olyan alanyokat teszteltek, akiknél valamilyen, a kísérlettel nem összefüggő okból agyműtétre volt szükség, és hozzájárultak, hogy agyuk egyes pontjaira a szomatoszenzoros kéregben elektródákat helyezzenek el. Libet kísérletének eredménye az volt, hogy amikor az alanyok bőrét egy inger érte, tudatosan kb. fél másodperc múlva észlelték azt annak ellenére, hogy agyuk az inger jelét már egy századmásodperc alatt felfogta, és egy előreprogramozott „reflex” választ (lásd előbb) kb. egytized másodperc alatt adott (10.6. ábra). Mi több, mialatt az inger elérte a tudatot, az alanyoknak a fél másodperces késés ellenére az volt a szubjektív benyomásuk, hogy késés egyáltalán nem volt! (Más kísérleteiben Libet a talamuszt ingerelte, vö. 9. fejezet, hasonló eredményekkel.)
Emlékezzünk vissza, hogy a szomatoszenzoros kéreg a nagyagynak az a része, ahová az érzékszervi jelek belépnek. Így egy olyan pontjának elektromos ingerlése, amely a bőr egy meghatározott pontjának felel meg, egyenértékű azzal, mintha valami ténylegesen megérintette volna a bőrnek azt a pontját. Kiderül azonban, hogy ha ez az elektromos ingerlés túl rövid – kevesebb, mint kb. fél másodperc –, akkor az alanyban semmiféle érzés nem tudatosul. Ez ellentétben áll azzal, amikor a bőrnek azt a pontját közvetlenül ingerlik, mert a bőr pillanatszerű érintése is érezhető.
Tegyük most fel, hogy először megérintik a bőrt, utána ingerlik elektromosan a szomatoszenzoros kéreg megfelelő pontját. Mit érez a kísérleti alany? Ha az elektromos ingerlés a bőr érintése után kb. negyed másodperccel történik, akkor utóbbit egyáltalán nem érzi! Ezt a hatást nevezik visszafelé álcázásnak. A kéreg ingerlése megakadályozza a rendes bőrérintés tudatos érzékelését. A tudatos érzékelést megakadályozhatja („álcázhatja”) egy későbbi esemény, feltéve hogy kb. fél másodpercen belül bekövetkezik. Ez önmagában azt mondja nekünk, hogy egy ilyen érzékelés úgy fél másodperccel azután tudatosul, hogy a tényleges esemény kiváltja az érzékelést!
Úgy látszik azonban, hogy érzékelésünk ilyen hosszú időkésésének nem vagyunk „tudatában”. E furcsa eredmény egyik értelmezése lehet, ha azt képzeljük, hogy minden „érzékelésünk ideje” késik fél másodpercet a „tényleges időhöz” képest – mintha belső óránk egyszerűen „rossz” volna úgy fél másodperccel. Egy eseményt mindig fél másodperccel tényleges bekövetkezése után érzékelnénk. Ez következetes, bár a késés miatt zavaró képet festene érzéki benyomásainkról.
Talán valami ilyen természetű dolog derül ki Libet kísérletének második részéből, amikor először a kérget ingerelték elektromosan folyamatosan, fél másodpercnél jóval tovább, ezalatt, kevesebb, mint fél másodperccel az ingerlés kezdete után, a bőrt is megérintették. A kísérleti alanyok a kérgi ingerlést és a bőr érintését külön-külön érzékelték, és azokat világosan meg tudták egymástól különböztetni. Amikor azonban megkérdezték, melyik volt az első, az alany azt válaszolta, hogy a bőr érintése, annak ellenére, hogy a kérgi ingerlés megelőzte azt! Úgy látszik tehát, hogy az alany a bőrérintés érzékelését időben visszavonatkoztatja kb. fél másodperccel (lásd 10.6. ábra). Ám ez nem egyszerűen a belső időérzékelés általános „hibája”, hanem az események időbeli érzékelésének sokkal finomabb átrendezése. A kérgi ingerlést, feltéve, hogy ténylegesen nem érzékeljük később, mint kezdete után fél másodperccel, úgy látszik, nem vonatkoztatjuk vissza ezen a módon.
Az első kísérletből arra következtethetünk, hogy a tudatos cselekvés végrehajtása egy-másfél másodpercet vesz igénybe, míg a második kísérlet szerint egy külső esemény csak bekövetkezése után fél másodperccel tudatosul. Képzeljük el, mi történik, ha valamilyen előre nem látott külső eseményre válaszolunk. Tegyük fel, hogy a válasz egy pillanatnyi tudatos elmélkedést kíván. Libet eredményei alapján úgy látszik, hogy fél másodpercnek kell eltelnie, mielőtt a tudatosság belép; utána pedig, amint azt Kornhuber adatai sugallják, jó egy másodpercre van szükség, míg az „akarati” válasz életbe léphet. Az egész folyamat az érzéki bemenettől a motoros kimenetig úgy két másodpercet vesz igénybe! E két kísérlet nyilvánvaló együttes tanulsága: a tudatosság egyáltalán nem játszhat szerepet egy külső eseményre adott válaszban, ha azt két másodpercen belül kell megadni!
Az idő különös szerepe a tudatos érzékelésben
Elfogadhatjuk-e szó szerint ezeket a kísérleteket? Ha igen, akkor arra a következtetésre jutunk, hogy amikor olyan tettet hajtunk végre, amellyel egy választ kevesebb mint egy vagy két másodperc alatt módosítunk, akkor teljesen „automataként” cselekszünk. A tudatosság kétségtelenül lassú az idegrendszer más mechanizmusaihoz képest. Magam is észrevettem eseteket, például azt, hogy reménytelenül figyelem kezemet, amint bezárja az autó ajtaját egy pillanattal azután, hogy észrevettem valamit bent az autóban, amit ki akartam venni, és akarati utasításom kezem mozgásának megállítására zavarbeejtően lassan hajtódik végre – túl lassan ahhoz, hogy megállítsam az ajtó becsukását. De tart-e ez egy egész másodpercig vagy kettőig? Ilyen hosszú idő nekem valószínűtlennek tetszik. Természetesen tudatos tudomásom a kocsiban lévő tárgyról és vele együtt a kezeimet megállító utasítás elképzelt „szabad akarata” nyugodtan bekövetkezhetne mindkét esemény után. A tudatosság esetleg csupán szemlélő, aki csak „visszajátssza” az egész drámát. Hasonlóképpen az előző eredmények alapján, ránézésre, a tudatosságnak nem volna ideje, hogy bármilyen szerepet játsszon, amikor például a teniszező üt egyet – a pingpongozóról nem is beszélve! Nem kétséges, hogy e játékok mesterei válaszaik minden lényegét kisagyi szabályozásban birtokolják szuper módon előreprogramozva. Ám hogy a tudatosság egyáltalán semmi szerepet ne játsszon az elhatározásokban, hogy mikor milyen ütést csináljanak, ezt kissé nehéz elhinni. Bizonyára sok mindent előre látnak, hogy mit csinálhat az ellenfél, és lehetséges megmozdulásaira sok előreprogramozott válasz létezik, de ez nekem hasznavehetetlennek látszik, és nehezen fogadnám el a tudatosság belekeveredésének teljes hiányát. Ezek a megjegyzések még inkább érvényesek a rendes beszélgetésre. Részben ugyan előre tudhatjuk, mit fog a másik mondani, ám gyakran kell legyen váratlan dolog a másik megjegyzéseiben, különben a beszélgetés teljesen szükségtelen volna! Bizonyára nem tesz ki két másodpercet, hogy rendes beszélgetés során valakinek válaszoljunk!
Talán van okunk kételkedni abban, hogy Kornhuber kísérletei azt bizonyítják, hogy a tudatosság „tényleges” működésére másfél másodpercre van szükség. Noha igaz, hogy az ujj behajlításának az EEG-felvételeken látható szándéka átlagosan ilyen korán jelentkezik, meglehet, hogy csak egyes esetekben van meg ennyire előre a szándék – és e tudatos szándék gyakran ténylegesen nem valósulhat meg –, míg sok más esetben a tudati működés ennél sokkal közelebb van az ujj behajlításához.
Tegyük fel egy pillanatra, hogy mindkét kísérleti következtetés érvényes. Szeretnék egy riasztó javaslatot tenni ezzel kapcsolatban. Lehet, hogy nagyon rosszat teszünk, amikor a tudatossággal kapcsolatban az időre a szokásos fizikai szabályokat alkalmazzuk! Az idő valóban bármelyik esetben nagyon furcsa módon lép be tudatos felfogásunkba, és lehetségesnek hiszem, hogy egészen más fogalmakra van szükség, amikor a tudatos felfogást egy hagyományos időrendezett keretben próbáljuk elhelyezni. A tudatosság végül is az egyetlen ismert jelenség, amely szerint az időnek egyáltalán „folynia” kell! A modern fizikában az időt lényegében ugyanúgy kezdjük, mint a teret,188 és a fizikai leírásokban az idő valójában egyáltalán nem „folyik”; egy statikusnak látszó, rögzített „téridőnk” van, amelyben világegyetemünk eseményei elrendeződnek! Érzékeléseink szerint azonban az idő mégis folyik (lásd 7. fejezet). Sejtésem az, hogy itt valami érzékszervi csalódásról is szó lehet, és az idő „igazából” nem egészen azon a lineáris, előrehaladó módon folyik, ahogy azt érzékeljük (akármit is jelentsen ez!). Az időrend, amelyet érzékelni „látszunk”, azt állítom, valami olyan, amivel rászedjük érzékeléseinket, hogy azok értelmet nyerjenek egy külső fizikai valóság egyenletesen előrehaladó idejével kapcsolatban.
Egyesek jó adag filozófiai „tévedést” fedezhetnek fel az előbbi megjegyzésekben – és ebben kétségtelenül igazuk is volna. Hogyan „tévedhetünk” abban, amit ténylegesen érzékelünk? Az érzékelések definíció szerint éppen azok a dolgok, amelyekről közvetlenül szerzünk tudomást, így ebben nem lehet „tévedni”. Mindazonáltal úgy vélem, hogy az időbeli haladás érzékelésében valószínűleg „tévedünk” (annak ellenére, hogy a közönséges nyelv elégtelen ennek leírására), és ennek alátámasztására van bizonyíték (lásd Churchland 1984).
Egy szélsőséges példa Mozartnak az a képessége, hogy „egy villanás alatt elkapjon” egy teljes zenei kompozíciót, „bármilyen hosszú is az”. Mozart leírása alapján fel kell tételeznünk, hogy ez a „villanás” tartalmazta a teljes kompozíció lényegét, noha e tudatos felfogás tényleges külső időtartama, a szokásos fizikai értelemben semmiképpen sem lehetett összehasonlítható a kompozíció eljátszásához szükséges idővel. Elképzelhető, hogy Mozart felfogásának más formája lehetett, talán térbeli, mint egy vizuális jelenet, vagy egy teljes megírt kotta. De még ez utóbbi átolvasása is komoly időt venne igénybe – és nagyon kétlem, hogy Mozart kezdetben ilyen formában érzékelte volna kompozícióit (bizonyára megemlítette volna!). Leírásához jobban illik a vizuális jelenet, ám (a hozzám közelebb álló, legközönségesebb matematikai képanyagot ismerve) nagyon kétlem, hogy valami olyanról van szó, mint a zene közvetlen lefordítása vizuális alakra. Sokkal valószínűbbnek látszik, hogy Mozart „villanását” tisztán zeneinek kell elfogadnunk, azzal a határozott időbeli értelemmel, amit egy zenedarab meghallgatása (vagy lejátszása) jelent. A zene hangokból áll, amelyeknek meghatározott az ideje, ahogy Mozart leírásában „… képzeletem hallani engedi.”
Hallgassuk meg a négyszeres fúgát J. S. Bach A fúga művészete befejező részében. Aki valamit érez Bach zenéje iránt, azt biztosan megindítja, amikor tíz perc után, éppen a harmadik téma belépését követően a zene abbamarad. A kompozíció mint egész még „ott” látszik lebegni, de egy pillanat alatt eltűnik előlünk. Bach meghalt, mielőtt a művet be tudta volna fejezni, a hangjegyek ezen a ponton egyszerűen megszakadnak, semmi írásos jele nincsen, hogyan akarta folytatni. Mégis olyan biztonsággal és mesterien indul, hogy el sem tudjuk képzelni, hogy az egész kompozíció lényege ne lett volna egyszerre Bach fejében. Le kellett-e játszania magának fejben az egészet a rendes előadási ütemben mindig újra és újra, amikor a különböző javítások felötlöttek benne? Nem tudom elképzelni, hogy így történt. Hasonlóan Mozarthoz, ő is képes kellett legyen, hogy művét, benne a fúga minden bonyolultságát, tekervényét, művészetét, az egészet egyszerre felidézve, teljességében felfogja. A zene egyik lényeges alkotórésze mégis az időbeli lefolyása. Hogyan lehetséges, hogy a zene zene marad, ha nem „valós időben” játszódik le?
Egy regény vagy egy történet kigondolása hasonló (bár kevésbé rejtélyesnek látszó) problémát vethet fel. Egy egyén egész életének elképzelésénél különféle eseményeket kellene átgondolni, amelyek megfelelő értékelése látszólag „valós idejű” szellemi munkát követelne meg. Azonban úgy látszik, még sincs erre szükség. Még a saját időfogyasztó tapasztalataink emlékeinek lenyomatai is valahogy úgy össze vannak „sűrítve”, hogy jóformán az emlékezés egy pillanata alatt „újraélhetjük” azokat!
Lehet talán valami komoly hasonlóság a zeneszerzés és a matematikai gondolkodás között. Az emberek azt gondolhatják, hogy egy matematikai bizonyítás logikus folyamatként születik meg, amelyben minden egyes lépés a megelőzőből következik. Egy új gondolatmenet azonban aligha ezen a módon keletkezik. Az átfogó jelleg és a látszólag homályos fogalmi tartalom az, ami egy matematikai bizonyítás létrejöttéhez szükséges; és ez időben egész mást jelent, mint amennyit egy megfelelő sorrendben előadott bizonyítás teljes megértése igényel.
Tegyük fel hát, hogy elfogadjuk, a tudatosság üteme és időbeli haladása nincs összhangban a külső fizikai valóságéval. Nem fenyeget-e az, hogy paradoxonhoz jutunk? Tegyük fel, hogy mégis van valami teleologikus a tudatosság hatásaiban, azaz egy későbbi benyomás befolyásolhat egy múltbeli cselekvést. Biztosan olyan ellentmondásokra vezetne-e ez, mint paradox velejáróival a fénynél gyorsabb jeladás, amelyet vizsgáltunk – és ki is zártunk – az 5. fejezet vége felé? Azt szeretném sugallni, hogy nem kell legyen paradoxon – a tudatosság igazi természeténél fogva, amelyet bizonygatok. Emlékezzünk javaslatomra, hogy a tudatosság lényegében a szükségszerű igazság „látása”; és hogy valamiféle tényleges kapcsolatot jelenthet az ideális matematikai fogalmak platóni világával. Platón világa maga időtlen. A platóni igazság érzékelése nem hordoz tényleges információt – az „információ” technikai értelmében, hogy üzenetben át lehet azt adni –, és nem jelentene tényleges ellentmondást az, ha az ilyen tudatos érzékelés esetleg visszafelé terjedne az időben!
De még ha el is fogadjuk, hogy a tudatosság ilyen különös viszonyban áll az idővel, és hogy valamilyen értelemben kapcsolatot jelent a külső fizikai világ és valami időtlen között; hogyan illeszthető ez össze az anyagi agy fizikailag meghatározott és időrendezett működésével? Úgy látszik, a tudatosságnak megint csak a „szemlélő” szerepe marad, ha nem akarunk a fizikai törvények rendes haladásával manipulálni. Én mégis védem a tudatosság valamiféle aktív és erőteljes szerepét, amely komoly kiválasztódási előnyt biztosít. Hiszem, hogy a dilemmára a válasz abban a különös módban rejlik, ahogy a KKG-nek működnie kell, hogy feloldja az ellentétet a két kvantummechanikai folyamat, az U és az R között.
Emlékezzünk vissza, milyen problémák merülnek fel az idővel kapcsolatban, amikor az R eljárást összhangba próbáljuk hozni a (speciális) relativitáselmélettel (6. és 8. fejezet). Az eljárásnak, a közönséges téridőfogalmakkal leírva, egyáltalán nem látszik értelme. Tekintsük egy részecskepár valamely kvantumállapotát. Egy ilyen állapot általában korrelált (azaz nem egyszerűen |ψ〉∣χ〉 alakú, ahol |ψ〉 és ∣χ〉 az egyik, illetve másik részecskét írja le, hanem egy |ψ〉∣χ〉 + |α〉∣β〉 + … + |ρ〉∣σ〉) alakú összeg). Így az egyik részecske megfigyelése nemlokális módon befolyásolja a másikat, és ez nem írható le a rendes téridőfogalmakkal a speciális relativitáselmélettel összhangban (EPR; az Einstein–Podolsky–Rosen-jelenség). Ilyen nemlokális jelenségeket hallgatólagosan tartalmaz javasolt analógiám a kvázikristályok és a dendrittüskék növekedése és összehúzódása között.
A megfigyelést itt úgy értelmezem, mint az egyes megfigyelt részecskék viselkedésének felnagyítását, amíg a KKG „egygraviton-feltételéhez” valami hasonló teljesül. A „hagyományosabb” fogalmakban egy „megfigyelés” sokkal bizonytalanabb dolog, és nehéz látni, hogyan lehetne az agyműködés kvantumelméleti leírását kidolgozni, amikor az agy nyugodtan tekinthető úgy, hogy mindvégig „saját magát figyeli meg”!
Elképzelésem másrészt az, hogy a KKG az állapotvektor redukciójának (R) objektív fizikai elméletét szolgáltatja, amelynek nem kell függnie a tudatosságtól. Ilyen elméletünk még nincs, de legalább megtalálását nem gátolják azok a mély problémák, hogy mi is valójában a tudatosság!
Azt jósolom, hogy ha egyszer a KKG-t valóban megtalálják, akkor ezzel majd lehetségessé válik a tudatosság jelenségének megmagyarázása. Úgy gondolom, hogy amikor majd meglesz, akkor a KKG tulajdonságai még távolabb lesznek a hagyományos téridőleírástól, mint amennyire azt a titokzatos kétrészecskés EPR-jelenség megköveteli. Ha, amint sejtem, a tudatosság jelensége e feltételezett KKG-n alapszik, akkor a tudatosság maga is csak nagyon nehezen illeszthető be a jelenlegi, hagyományos téridőleírásba!
188 Ez a szimmetria a tér és az idő között még feltűnőbb volna egy kétdimenziós téridőben. A fizika egyenletei az utóbbiban lényegében szimmetrikusak volnának a tér és az idő felcserélésével szemben – mégse mondaná senki, hogy a kétdimenziós fizikában a tér „folyik”. Nehéz elhinni, hogy a fizikai világról szerzett tapasztalatainkban azért észleljük az idő „folyását”, mert történetesen aszimmetria van a tér és az idő dimenzióinak számai között (3, illetve 1).
1./
Hallgassuk meg a négyszeres fúgát J. S. Bach A fúga művészete befejező részében. Aki valamit érez Bach zenéje iránt, azt biztosan megindítja, amikor tíz perc után, éppen a harmadik téma belépését követően a zene abbamarad. A kompozíció mint egész még „ott” látszik lebegni, de egy pillanat alatt eltűnik előlünk. Bach meghalt, mielőtt a művet be tudta volna fejezni, a hangjegyek ezen a ponton egyszerűen megszakadnak, semmi írásos jele nincsen, hogyan akarta folytatni. Mégis olyan biztonsággal és mesterien indul, hogy el sem tudjuk képzelni, hogy az egész kompozíció lényege ne lett volna egyszerre Bach fejében. Le kellett-e játszania magának fejben az egészet a rendes előadási ütemben mindig újra és újra, amikor a különböző javítások felötlöttek benne? Nem tudom elképzelni, hogy így történt. Hasonlóan Mozarthoz, ő is képes kellett legyen, hogy művét, benne a fúga minden bonyolultságát, tekervényét, művészetét, az egészet egyszerre felidézve, teljességében felfogja. A zene egyik lényeges alkotórésze mégis az időbeli lefolyása. Hogyan lehetséges, hogy a zene zene marad, ha nem „valós időben” játszódik le?
Egy regény vagy egy történet kigondolása hasonló (bár kevésbé rejtélyesnek látszó) problémát vethet fel. Egy egyén egész életének elképzelésénél különféle eseményeket kellene átgondolni, amelyek megfelelő értékelése látszólag „valós idejű” szellemi munkát követelne meg. Azonban úgy látszik, még sincs erre szükség.
2./
Még a saját időfogyasztó tapasztalataink emlékeinek lenyomatai is valahogy úgy össze vannak „sűrítve”, hogy jóformán az emlékezés egy pillanata alatt „újraélhetjük” azokat!
3./
Így az egyik részecske megfigyelése nemlokális módon befolyásolja a másikat, és ez nem írható le a rendes téridőfogalmakkal a speciális relativitáselmélettel összhangban (EPR; az Einstein–Podolsky–Rosen-jelenség). Ilyen nemlokális jelenségeket hallgatólagosan tartalmaz javasolt analógiám a kvázikristályok és a dendrittüskék növekedése és összehúzódása között.
A megfigyelést itt úgy értelmezem, mint az egyes megfigyelt részecskék viselkedésének felnagyítását, amíg a KKG „egygraviton-feltételéhez” valami hasonló teljesül. A „hagyományosabb” fogalmakban egy „megfigyelés” sokkal bizonytalanabb dolog, és nehéz látni, hogyan lehetne az agyműködés kvantumelméleti leírását kidolgozni, amikor az agy nyugodtan tekinthető úgy, hogy mindvégig „saját magát figyeli meg”!
Elképzelésem másrészt az, hogy a KKG az állapotvektor redukciójának (R) objektív fizikai elméletét szolgáltatja, amelynek nem kell függnie a tudatosságtól. Ilyen elméletünk még nincs, de legalább megtalálását nem gátolják azok a mély problémák, hogy mi is valójában a tudatosság!
Azt jósolom, hogy ha egyszer a KKG-t valóban megtalálják, akkor ezzel majd lehetségessé válik a tudatosság jelenségének megmagyarázása. Úgy gondolom, hogy amikor majd meglesz, akkor a KKG tulajdonságai még távolabb lesznek a hagyományos téridőleírástól, mint amennyire azt a titokzatos kétrészecskés EPR-jelenség megköveteli. Ha, amint sejtem, a tudatosság jelensége e feltételezett KKG-n alapszik, akkor a tudatosság maga is csak nagyon nehezen illeszthető be a jelenlegi, hagyományos téridőleírásba!
Következtetés: egy gyermek nézőpontja
E könyvben sok érvet hoztam fel, hogy megmutassam annak a – jelenlegi filozófiában eléggé uralkodó – nézőpontnak a tarthatatlanságát, hogy gondolkodásunk alapvetően egy nagyon bonyolult számítógép működésével azonos. Az „EMI” – Searle nevezte el így – azzal a kifejezett feltevéssel él, hogy egy algoritmusnak csupán a működtetése kiválthatja a tudatosságot. Kevésbé határozott összefüggésekben használnak olykor más elnevezéseket is, mint például a „funkcionalizmust”.
Egyes Olvasók esetleg a kezdettől fogva szalmabábnak képzelhetik az „EMI pártolóját”! Nem „nyilvánvaló”-e, hogy a puszta számítás nem ébreszthet örömöt vagy fájdalmat; hogy az illető nem foghatja fel a költészetet vagy az esti égbolt szépségét vagy a hangok varázsát; hogy nem reménykedhet, szerethet vagy gyötrődhet; hogy nem lehet igazi, önálló célja? A tudomány mintha mégis el akarná fogadtatni velünk, hogy mindnyájan csupán kis részei vagyunk egy világnak, amelyet minden részletében (még ha esetleg valószínűségi módon is) nagyon pontos matematikai törvények irányítanak. Agyunk, amely minden cselekedetünket vezérelni látszik, maga is ugyanezen pontos törvények irányítása alatt áll. Kialakult az a kép, hogy mindez a pontos fizikai tevékenység tulajdonképpen nem más, mint egy hatalmas (esetleg valószínűségi) számítás eredménye – és így agyunk és értelmünk megérthető pusztán ilyen számítások segítségével. Amikor a számítások rendkívül bonyolulttá válnak, akkor agyunk esetleg költőibb vagy szubjektívabb minőségeket kezdhet magára ölteni, ezeket társítjuk az „értelem” fogalmával. Mégis nehéz megszabadulni attól a kényelmetlen érzéstől, hogy az ilyen képből valaminek mindig hiányoznia kell.
Érveimmel mindig ezt a nézetet próbáltam támogatni, hogy valóban kell valami lényegesnek lennie, ami hiányzik a tisztán számításközpontú képekből. Mégis kitartok a remény mellett, hogy az értelem megértésében a természettudományokon és a matematikán keresztül kell komoly előrehaladásnak létrejönnie. A dilemma látható, ám próbáltam megmutatni, hogy van igazi, kifelé vezető út. A kiszámítható egyáltalán nem azonos a matematikailag pontossal. A pontos platóni matematikai világban annyi a titokzatosság és a szépség, amennyit csak kívánni lehet, és ennek legnagyobb része olyan fogalmakban rejtőzik, amelyek kívül esnek azon a viszonylag szűk részen, amelyet az algoritmusok és a számítás foglal el.
A tudatosság számomra olyan fontos jelenségnek látszik, hogy egyszerűen nem tudom elhinni, hogy egy bonyolult számítás „véletlenül” kiválthatja. Ez az a jelenség, amely által a világegyetem létezése ismertté válik. Lehet úgy érvelni, hogy egy, a tudatosságot kizáró törvények alatt álló világegyetem egyáltalán nem is világegyetem. Én még azt is mondanám, hogy a világegyetem eddigi matematikai leírásai nem teljesíthetik ezt a feltételt. Csak a tudatosság jelensége adhat tényleges létezést egy feltételezett, „elméleti” világegyetemnek!
E fejezetekben leírt egyes gondolatmeneteim tekervényeseknek és bonyolultaknak tűnhetnek. Vannak olyanok, amelyek bevallottan spekulatívak, de hiszem, hogy vannak elkerülhetetlenek is. Ám mind e szakmai kérdések mögött ott van az érzés, hogy valóban „nyilvánvaló”: a tudatos értelem nem működhet úgy, mint egy számítógép, még ha a szellemi tevékenység jelentős részére ez nem is áll fenn.
Ezt a nyilvánvalóságot egy gyermek is láthatja – bár később, élete során megfélemlítve hiheti azt, hogy a nyilvánvaló problémák „nem problémák”, hogy megfelelő okfejtéssel és a definíciók okos megválasztásával a nemlétezésbe terelhetők. A gyermekek olykor világosnak látnak olyan dolgokat, amelyek később valóban homályosaknak bizonyulnak. Gyakran elfelejtjük a kíváncsiságot, amelyet gyermekként éreztünk, mihelyt a „való világ” működésének gondjai kezdik nyomni vállunkat. A gyermekek nem félnek alapvető kérdéseket feltenni, amelyekkel szemben nekünk, felnőtteknek, gátlásaink vannak. Mi történik tudatosságunkkal, miután meghalunk; hol volt az, mielőtt megszülettünk; válhatunk-e valaki mássá, voltunk-e valaki más; miért érzékelünk egyáltalán; miért vagyunk itt; miért van egyáltalán világegyetem, amelyben élhetünk? Titkok ezek, amelyek a tudatosság – és nem kétséges, hogy az igazi öntudat – ébredezésekor érnek el hozzánk.
Emlékszem, gyermekként sok ilyen rejtély foglalkoztatott. Hogy tudatom esetleg kicserélődhet valaki máséval. Hogyan tudhatnám meg valaha, hogy korábban nem történhetett-e velem ilyen – feltéve, hogy mindenki csak az „éppen maga” emlékeit hordozza? Hogyan tudnám elmagyarázni az ilyen „cserét” valaki másnak? Jelent-e ez egyáltalán valamit? Talán egyszerűen ugyanazon tíz perc tapasztalatait élem meg újra és újra, mindig pontosan ugyanazokkal az érzékelésekkel. Esetleg csak a jelen pillanat „létezik” számomra? A holnapi vagy a tegnapi „énem” talán egy egészen különböző, független tudatú személy. Talán visszafelé élek az időben, tudatosságom visszafelé áramlik az időben, emlékezetem tulajdonképpen azt mondja, mi fog történni, és nem azt, mi történt velem – egy kellemetlen iskolai tapasztalat az valami, ami még előttem áll, és sajnos rövidesen be fog következni. Ez utóbbi és a rendesen tapasztalt időhaladás megkülönböztetése „jelent-e” tulajdonképpen valamit, mondjuk hogy az egyik „rossz” és a másik „helyes”? Hogy az ilyen kérdések elvileg megválaszolhatók legyenek, ahhoz a tudatosság elméletére volna szükség. Ám hogyan kezdhetnénk egyáltalán magyarázni az ilyen problémák lényegét annak, aki maga nem volt tudatos…?
1./ És tulajdonképpen itt a vége, vagy nem vége:
Érveimmel mindig ezt a nézetet próbáltam támogatni, hogy valóban kell valami lényegesnek lennie, ami hiányzik a tisztán számításközpontú képekből. Mégis kitartok a remény mellett, hogy az értelem megértésében a természettudományokon és a matematikán keresztül kell komoly előrehaladásnak létrejönnie. A dilemma látható, ám próbáltam megmutatni, hogy van igazi, kifelé vezető út. A kiszámítható egyáltalán nem azonos a matematikailag pontossal. A pontos platóni matematikai világban annyi a titokzatosság és a szépség, amennyit csak kívánni lehet, és ennek legnagyobb része olyan fogalmakban rejtőzik, amelyek kívül esnek azon a viszonylag szűk részen, amelyet az algoritmusok és a számítás foglal el.
A tudatosság számomra olyan fontos jelenségnek látszik, hogy egyszerűen nem tudom elhinni, hogy egy bonyolult számítás „véletlenül” kiválthatja. Ez az a jelenség, amely által a világegyetem létezése ismertté válik. Lehet úgy érvelni, hogy egy, a tudatosságot kizáró törvények alatt álló világegyetem egyáltalán nem is világegyetem. Én még azt is mondanám, hogy a világegyetem eddigi matematikai leírásai nem teljesíthetik ezt a feltételt. Csak a tudatosság jelensége adhat tényleges létezést egy feltételezett, „elméleti” világegyetemnek!
E fejezetekben leírt egyes gondolatmeneteim tekervényeseknek és bonyolultaknak tűnhetnek. Vannak olyanok, amelyek bevallottan spekulatívak, de hiszem, hogy vannak elkerülhetetlenek is. Ám mind e szakmai kérdések mögött ott van az érzés, hogy valóban „nyilvánvaló”: a tudatos értelem nem működhet úgy, mint egy számítógép, még ha a szellemi tevékenység jelentős részére ez nem is áll fenn.
Ezt a nyilvánvalóságot egy gyermek is láthatja – bár később, élete során megfélemlítve hiheti azt, hogy a nyilvánvaló problémák „nem problémák”, hogy megfelelő okfejtéssel és a definíciók okos megválasztásával a nemlétezésbe terelhetők. A gyermekek olykor világosnak látnak olyan dolgokat, amelyek később valóban homályosaknak bizonyulnak. Gyakran elfelejtjük a kíváncsiságot, amelyet gyermekként éreztünk, mihelyt a „való világ” működésének gondjai kezdik nyomni vállunkat. A gyermekek nem félnek alapvető kérdéseket feltenni, amelyekkel szemben nekünk, felnőtteknek, gátlásaink vannak
Epilógus
„… hogy mit érez? Oh, … ez igen érdekes kérdés, kisfiam … hm … magam is kíváncsi vagyok a válaszra” – mondta a Főtervező. – „Nézzük, mit mond barátunk … ez különös … hm … Ultronic azt mondja, nem tudja, mi az … nem is érti, mire akarsz kilyukadni!” A teremben a nevetés hullámai hahotába csaptak át.
Adam nagy zavarban érezte magát. Viselkedjenek akárhogy, de nevetniük azért nem kellene.
Irodalom
Aharonov, Y. – Albert, D. Z. (1981): Can we make sense out of the measurement process in relativistic quantum mechanics? Phys. Rev. D24, 359–70.
Aharonov, Y. – Bergmann, P. – Lebowitz, J. L. (1964): Time symmetry in the quantum process of measurement. In Quantum theory and measurement (ed. J. A. Wheeler and W. H. Zurek). Princeton University Press, Princeton, NJ. 1983; az eredeti in Phys. Rev. 134B, 1410–16.
Ashtekar, A. – Balachandran, A. P. – Sang Jo (1989): The CP problem in quantum gravity. Int. J. Mod. Phys. A6, 1493–514.
Aspect, A. – Grangier, P. (1986): Experiments on Einstein–Podolsky–Rosen-type correlations with pairs of visible photons. In Quantum concepts in space and time (ed. R. Penrose and C. J. Isham). Oxford University Press, Oxford.
Atkins, P. W. (1987): Why mathematics works. Oxford University Extension Lecture in series: Philosophy and the New Physics (13 March).
Barrow, J. D. (1988): The world within the world. Oxford University Press, Oxford.
Barrow, J. D. – Tipler, F. J. (1986): The anthropic cosmological principle. Oxford University Press, Oxford.
Baylor, D. A. – Lamb, T D. – Yau, K.-W. (1979): Responses of retinal rods to single photons. J. Physiol. 288, 613–34.
Bekenstein, J. (1972): Black holes and entropy. Phys. Rev. D7, 2333–46.
Belinfante, F J. (1975): Measurement and time reversal in objective quantum theory. Pergamon Press, New York.
Belinskii, V. A. – Khalatnikov, I. M. – Lifshitz, E. M. (1970): Oscillatory approach to a singular point in the relativistic cosmology. Adv. Phys. 19, 525–573.
Bell, J. S. (1987): Speakable and unspeakable in quantum mechanics. Cambridge University Press, Cambridge.
Benacerraf, P. (1967): God, the Devil and Gödel. The Monist 51, 9–32.
Blakemore, C. – Greenfield, S. (ed.) (1987): Mindwaves: thoughts on intelligence, identity and consciousness. Basil Blackwell, Oxford.
Blum, L. – Shub, M. – Smale, S. (1989): On a theory of computation and complexity over the real numbers: NP completeness, recursive functions and universal machines. Bull. Amer. Math. Soc. (In press.)
Bohm, D. (1951): The Paradox of Einstein, Rosen and Podolsky. In Quantum theory and measurement (ed. J. A. Wheeler and W. H. Zurek). Princeton University Press, Princeton, NJ. 1983; az eredeti in Quantum theory, D. Bohm, Ch. 22, sect. 15 –19. Prentice-Hall, Englewood-Cliffs.
Bohm, D. (1952): A suggested interpretation of the quantum theory in terms of ‘hidden’ variables, I and II. In Quantum theory and measurement (ed. J. A. Wheeler and W. H. Zurek), Princeton University Press, 1983; az eredeti in Phys. Rev. 85, 166–93.
Bondi, H. (1960): Gravitational waves in general relativity. Nature (London), 186, 535.
Bowie, G. L. (1982): Lucas’ number is finally up. J. of Philosophical Logic, 11, 279–85.
Cartan, É. (1923): Sur les variétés a connexion affine et la théorie de la relativité generalisée. Ann. Sci. Ec. Norm. Sup. 40, 325 – 412.
Chandrasekhar, S. (1987): Truth and beauty: aesthetics and motivations in science, University of Chicago Press, Chicago, Mic.
Church, A. (1941): The calculi of lambda-conversion. Annals of Mathematics Studies, no. 6. Princeton University Press, Princeton, NJ.
Churchland, P. M. (1984): Matter and consciousness. Bradford Books, MIT Press, Cambridge, Mass.
Clauser, J. F. et al. (1969): Proposed experiment to test local hidden-variable theories. In Quantum theory and measurement (ed. J. A. Wheeler and W. H. Zurek), Princeton University Press, Princeton, NJ. 1983; az eredeti in Phys. Rev. Lett. 23, 880–84.
Close, E. (1983): The cosmic orion: quarks and the nature of the universe. Heinemann, London.
Cohen, P. C. (1966): Set theory and the continuum hypothesis, Benjamin, Menlo Park, CA.
Cutland, N. J. (1980): Computability: an introduction to recursive function theory. Cambridge University Press.
Davies, P. C. W. (1974): The physics of time-asymmetry. Surrey University Press.
Davies, P. C. W – Brown, J. (1988): Superstrings: a theory of everything? Cambridge University Press.
Davies, R. D. et al. (1987): Sensitive measurement of fluctuations in the cosmic microwave background. Nature, 326, 462–5.
Davis, M. (1988): Mathematical logic and the origin of modern computers. In The universal Turing machine: a half-century survey (ed. R. Herken), Kammerer & Unverzagt, Hamburg.
Dawkins, R. (1986): The blind watchmaker. Longman, London.
de Broglie, L. (1956): Tentative d’interpretation causale et nonlineaire de la mechanique ondulatoire. Gauthier-Villars, Paris.
Deeke, L. – Grötzinger, B. – Kornhuber, H. H. (1976): Voluntary finger movements in man: cerebral potentials and theory. Biol. Cybernetics, 23, 99.
Delbrück, M. (1986): Mind from matter? Blackwell Scientific Publishing, Oxford. Dennett, D. C. (1978): Brainstorms. Philosophical Essays on Mind and Psychology, Harvester Press, Hassocks, Sussex.
Deutsch, D. (1985): Quantum theory, the Church–Turing principle and the universal quantum computer. Proc. Roy. Soc. (Lond.) A400, 97–117.
Devlin, K. (1988): Mathematics: the new golden age. Penguin Books, London.
De Witt, B. S. – Graham, R. D. (ed.) (1973): The many-worlds interpretation of quantum mechanics. Princeton University Press, Princeton, NJ.
Dirac, P. A. M. (1928): The quantum theory of the electron. Proc. Roy. Soc., London, A117 610–24; ditto, part II, ibid, A118, 361.
Dirac, P. A. M. (1938): Classical theory of radiating electrons. Proc. Roy. Soc. (London) A167, 148.
Dirac, P. A. M. (1939): The relations between mathematics and physics. Proc. Roy. Soc. (Edinburgh) 59, 122.
Dirac, P. A. M. (1947): The principles of quantum mechanics (3rd ed.). Oxford University Press, Oxford.
Dirac, P. A. M. (1982): Pretty mathematics. Int. J. Theor. Phys. 21, 603–5.
Drake, S. (trans.) (1953). Galileo Galilei: dialogue concerning the two chief world systems – Ptolemaic and Copernican. University of California, Berkeley, CA.
Drake, S. (1957): Discoveries and opinions of Galileo. Doubleday, New York.
Eccles, J. C. (1973): The understanding of the brain. McGraw-Hill, New York.
Einstein, A. – Podolsky, P. – Rosen, N. (1935): Can quantum-mechanical description of physical reality be considered complete? In Quantum theory and measurement (ed. J. A. Wheeler and W. H. Zurek). Princeton University Press, Princeton, NJ. 1983; az eredeti in Phys. Rev. 47, 777–80.
Everett, H. (1957): ‘Relative State’ formulation of quantum mechanics. In Quantum theory and measurement (ed. J. A. Wheeler and W. H. Zurek). Princeton University Press, Princeton, NJ.1983; az eredeti in Rev. of Mod. Phys. 29, 454–62.
Feferman, S. (1988): Turing in the Land of O(z). In The universal Turing machine: a half-century survey (ed. R. Herken), Kammerer & Unverzagt, Hamburg.
Feynman, R. P. – Leighton – Sands (1965): The Feynman Lectures. Addison-Wesley, Reading, MA.
Feynman, R. P. (1985): QED: the strange theory of light and matter. Princeton University Press, Princeton, NJ.
Fodor, J. A. (1983): The modularity of mind. MIT Press, Cambridge, MA.
Fredkin, E. – Toffoli, T. (1982): Conservative Logic. Int. J. Theor. Phys. 21, 219–53.
Freedman, S. J. – Clauser, J. F. (1972): Experimental test of local hidden-variable theories. In Quantum theory and measurement (ed. J. A. Wheeler and W. H. Zurek). Princeton University Press, Princeton, NJ. 1983; az eredeti in Phys. Rev. Lett. 28, 938–41.
Galilei, G. (1638): Dialogues concerning two new sciences. Macmillan edn. 1914; Dover Inc.
Gandy, R. (1988): The Confluences of Ideas in 1936. In The universal Turing machine: a half-century survey (ed. R. Herken). Kammerer & Unverzagt, Hamburg.
Gardner, M. (1958): Logic machines and diagrams. University of Chicago Press.
Gardner, M. (1983): The whys of a philosophical scrivener. William Morrow and Co., Inc., New York.
Gardner, M. (1989): Penrose tiles to trapdoor ciphers. W. Freeman, New York.
Gayle, E W. (1987): Free-surface solidification habit and point group symmetry of a faceted icosahedral Al-Li-Cu phase. J. Mater. Sci. 2, 1–4.
Gazzaniga, M. S. (1970): The bisected brain. Appleton-Century-Crofts, New York.
Gazzaniga, M. S. – LeDoux, J. E. – Wilson, D. H. (1977): Language, praxis, and the right hemisphere: clues to some mechanisms of consciousness. Neurology 27, 1144–7.
Geroch, R. – Hartle, J. B. (1986): Computability and physical theories. Found. Phys. 16, 533.
Ghirardi, G. C. – Rimini, A. – Weber, T. (1980): A general argument against superluminal transmission through the quantum mechanical measurement process. Lett. Nuovo. Cim. 27, 293–8.
Ghirardi, G. C. – Rimini, A. – Weber, T (1986): Unified dynamics for microscopic and macroscopic systems. Phys. Rev. D34, 470.
Gödel, K. (1931): Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I. Monatshefte für Mathematik und Physik 38, 173–98.
Good, I. J. (1969): Gödel’s theorem is a red herring. Brit. J. Philos. Sci. 18, 359–73.
Gregory, R. L. (1981): Mind in science; A history of explanations in psychology and physics. Weidenfeld and Nicholson Ltd.
Grey Walter, W. (1953): The living brain. Gerald Duckworth and Co. Ltd.
Grünbaum, B. – Shephard, G. C. (1981): Some problems on plane tilings. In The mathematical Gardner (ed. D. A. Klarner) Prindle, Weber and Schmidt, Boston.
Grünbaum, B. – Shephard, G. C. (1987): Tilings and patterns. Freeman, New York.
Hadamard, J. (1945): The psychology of invention in the mathematical field. Princeton University Press, Princeton, NJ.
Hanf, W. (1974): Nonrecursive filings of the plane, I. J. Symbolic Logic 39, 283–5.
Harth, E. (1982): Windows on the Mind. Harvester Press, Hassocks, Sussex.
Hartle, J. B. – Hawking, S. W. (1983): Wave function of the universe. Phys. Rev. D31, 1777.
Hawking, S. W. (1975): Particle creation by black holes. Commun. Math. Phys. 43, 199–220.
Hawking, S. W. (1987): Quantum cosmology. In 300 years of gravitation (ed. S. W. Hawking and W. Israel), Cambridge University Press, Cambridge.
Hawking, S. W. (1988): A brief history of time. Bantam Press, London.
Hawking, S. W. – Penrose, R. (1970): The singularities of gravitational collapse and cosmology. Proc. Roy. Soc. (London) A314, 529–48.
Hebb, D. O. (1954): The problem of consciousness and introspection. In Brain mechanisms and consciousness (ed. J. F. Delafresnaye). Blackwell, Oxford.
Hecht, S. – Shlaer, S. – Pirenne, M. H. (1941): Energy, quanta and vision. J. of Gen. Physiol. 25, 891–40.
Herken, R. ed. (1988): The universal Turing machine: a half-century survey Kammerer & Unverzagt, Hamburg.
Hiley, B. J. – Peat, E D., eds. (1987): Quantum implications. Essays in honour of David Bohm. Routledge and Kegan Paul, London & New York.
Hodges, A. P. (1983): Alan Turing: the enigma. Burnett Books and Hutchinson, London; Simon and Schuster, New York.
Hofstadter, D. R. (1979): Gödel, Escher, Bach: an eternal golden braid. Harvester Press, Hassocks, Sussex.
Hofstadter, D. R. (1981): A conversation with Einstein’s brain. In The mind’s I (ed. D. R. Hofstadter and D. C. Dennett) Basic Books, Inc.; Penguin Books, Ltd; Harmondsworth, Middx.
Hofstadter, D. R.–Dennett, D. C. (ed.) (1981): The mind’s I, Basic Books, Inc.; Penguin Books, Ltd; Harmondsworth, Middx.
Hubel, D. H. (1988): Eye, brain and vision. Scientific American Library Series # 22.
Huggett, S. A. – Tod, K. P. (1985): An introduction to twistor theory. London Math. Soc. student texts, Cambridge University Press, Cambridge.
Janes, J. (1980): The origin of consciousness in the breakdown of the bicameral mind. Penguin Books Ltd. Harmondsworth, Middx.
Kandel, E. R. (1976): The cellular basis of behaviour. Freeman, San Francisco.
Károlyházy, F. (1974): Gravitáció és a makroszkopikus testek kvantummechanikája. Magyar Fizikai Folyóirat 12, 24.
Károlyházy, F. – Frenkel, A. – Lukács, B. (1986): On the possible role of gravity on the reduction of the wave function. In Quantum concepts in space and time (ed. R. Penrose and C. J. Isham). Oxford University Press, Oxford.
Keene, R. (1988): Chess: Henceforward. The Spectator 261, (no. 8371), 52.
Knuth, D. M. (1981): The art of computer programming, Vol. 2 (2nd edn), Addison-Wesley, Reading, MA.
Komar, A. B. (1964): Undecidability of macroscopically distinguishable states in quantum field theory. Phys. Rev. 133B, 542–4.
Komar, A. B. (1969): Qualitative features of quantized gravitation. Int. J. Theor. Phys. 2, 157–60.
Kuznyecov, B. G. (1977): Einstein: Leben, Tod, Unsterblichkeit (trans. into German by H. Fuchs). Birkhauser, Basel.
LeDoux, J. E. (1985): Brain, mind and language. In Brain and mind (ed. D. A. Oakley). Methuen, London and New York.
Levy, D. W. L. (1984): Chess computer handbook, Batsford.
Libet, B. et al. (1979): Subjective referral of the timing for a conscious sensory experience. Brain 102, 193-224.
Lorenz, K. (1972): Quoted in: From ape to Adam by H. Wendt, Bobbs Merrill, Indianapolis.
Lucas, J. R. (1961): Minds, machines and Gödel. Philosophy, 36, 120–4; reprinted in Alan Ross Anderson (1964). Minds and machines, Englewood Cliffs.
MacKay, D. (1987): Divided brains–divided minds? In Mindwaves (ed. C. Blakemore and S. Greenfield). Basil Blackwell, Oxford.
Majorana, E. (1932): Atomi orientati in campo magnetico variabile. Nuovo Cimento, 9, 43–50.
Mandelbrot, B. B. (1986): Fractals and the rebirth of iteration theory. In The beauty of fractals: images of complex dynamical systems (ed. H.-O. Peitgen and P. H. Richter). Springer-Verlag, Berlin.
Maxwell, J. C. 1865): A dynamical theory of the electromagnetic field. Philos. Trans. Roy. Soc. (London) 155, 459–512.
Mermin, D. (1985): Is the moon there when nobody looks? Reality and the quantum theory. Physics Today 38 (no. 4), 38-47.
Michie, D. (1988): The fifth generation’s unbridged gap. In The universal Turing machine: a half-century survey (ed. R. Herken). Kammerer & Unverzagt, Hamburg.
Minsky, M. L. (1968): Matter, mind, and models. In Semantic information processing (ed. M. L. Minsky). M.I.T. Press, Cambridge, MA.
Misner, C. W. (1969): Mixmaster universe, Phys. Rev. Lett. 22, 1071–4.
Moruzzi, G. – Magoun, H. W. (1949): Brainstem reticular formation and activation of the EEG. Electroencephalography and Clinical Neurophysiology 1, 455–73.
Mott, N. F. (1929): The wave mechanics of α-ray tracks. In Quantum theory and measurement (ed. J. A. Wheeler and W. H. Zurek). Princeton University Press, Princeton, NJ. 1983; az eredeti in Proc. Roy. Soc. (London), A126, 79–84.
Mott, N. F. – Massey, H. S. W. (1965): Magnetic moment of the electron. In Quantum theory and measurement (ed. J. A. Wheeler and W. H. Zurek). Princeton University Press, Princeton, NJ. 1983; az eredeti in The theory of atomic collisions (ed. N. F. Mott and H. S. W Massey). Clarendon Press, Oxford.
Myers, D. (1974): Nonrecursive tilings of the plane, II. J. Symbolic Logic 39, 286–94.
Myers, R. E. – Sperry, R. W. (1953): Interocular transfer of a visual form discrimination habit in cats after section of the optic chiasm and corpus callosum. Anatomical Record 175, 351–2.
Nagel, E. – Newman, J. R. (1958): Gödel’s proof. Routledge & Kegan Paul, London and New York.
Nelson, D. R. – Halperin, B. I. (1985): Pentagonal and icosahedral order in rapidly cooled metals. Science 229, 233.
Neumann, J. (1955): Mathematical foundations of quantum mechanics. Princeton University Press, Princeton, NJ.
Newton, I (1730): Optics 1952 Dover, Inc.
Newton, I. (1687): Principia, Cambridge University Press, Cambridge.
Oakley, D. A. (ed.) (1985): Brain and mind. Methuen, London and New York.
Oakley, D. A. – Eames, L. C. (1985): The plurality of consciousness. In Brain and mind (ed. D. A. Oakley) Methuen, London and New York.
O’Connell, K. (1988): Computer chess. Chess 15.
O’Keefe, J. (1985): Is consciousness the gateway to the hippocampal cognitive map? A speculative essay on the neural basis of mind. In Brain and mind (ed. D. A. Oakley). Methuen, London and New York.
Onoda, G. Y. et al. (1988): Growing perfect quasicrystals. Phys. Rev. Lett. 60, 2688.
Oppenheimer, J. R. – Snyder, H. (1939): On continued gravitational contraction. Phys. Rev. 56, 455–9.
Pais, A. (1982): ‘Subtle is the Lord…’: the science and the life of Albert Einstein. Clarendon Press, Oxford.
Paris, J. – Harrington, L. (1977): A mathematical incompleteness in Peano arithmetic. In Handbook of mathematical logic (ed. J. Barwise). North-Holland, Amsterdam.
Pearle, P. (1985): ‘Models for reduction’. In Quantum concepts of space and time (ed. C. J. Isham and R. Penrose). Oxford University Press, Oxford.
Pearle, P. (1989): Combining stochastic dynamical state-vector reduction with spontaneous localization. Phys. Rev. A39, 2277–89.
Peitgen, H.-O. – Richter, P. H. (1986): The beauty of fractals. Springer Verlag, Berlin.
Peitgen, H.-O. – Saupe, D. (1988): The science of fractal images. Springer Verlag, Berlin.
Penfield, W. – Jasper, H. (1947): Highest Level Seizures. Research Publications of the Association for Research in Nervous and Mental Diseases (New York) 26, 252–71.
Penrose, R. (1965): Gravitational collapse and space-time singularities. Phys. Rev. Lett. 14, 57–9.
Penrose, R. (1974): The role of aesthetics in pure and applied mathematical research, Bull. Inst. Math. Applications 10 (no 7/8), 266–71.
Penrose, R. (1979a): Einstein’s vision and the mathematics of the natural world. The Sciences (March) 6–9.
Penrose, R. (1979b): Singularities and time-asymmetry. In General relativity: an Einstein centenary (ed. S. W. Hawking and W. Israel). Cambridge University Press, Cambridge.
Penrose, R. (1987a): Newton, quantum theory and reality. In 300 years of gravity (ed. S. W. Hawking and W. Israel). Cambridge University Press, Cambridge.
Penrose, R. (1987b): Quantum implications. Essays in honour of David Bohm. Routledge and Kegan Paul, London & New York.
Penrose, R. (1989a): Tilings and quasi-crystals; a non-local growth problem? In Aperiodicity and order 2 (ed. M. Jaric). Academic Press, New York.
Penrose, R. (1989b): Difficulties with inflationary cosmology, to appear in the Proceeding of the 14th Texas Symposium on Relativistic Astrophysics (ed. E. Fenves). NY Acad. Sci., New York.
Penrose, R. – Rindler, W. (1984): Spinors and space-time, Vol. 1: Two-spinor calculus and relativistic fields Cambridge University Press, Cambridge.
Penrose, R. – Rindler, W. (1986): Spinors and space-time, Vol. 2: Spinor and twistor methods in space-time geometry Cambridge University Press, Cambridge.
Pour-El, M. B. – Richards, I. (1979): A computable ordinary differential equation which possesses no computable solution. Ann. Math. Logic 17, 61–90.
Pour-El, M. B. – Richards, I. (1981): The wave equation with computable initial data such that its unique solution is not computable. Adv. in Math. 39, 215–39.
Pour-El, M. B. – Richards, I. (1982): Noncomputability in models of physical phenomena. Int. J. Theor. Phys. 21, 553–5.
Rae, A. (1986): Quantum physics: illusion or reality? Cambridge University Press, Cambridge.
Resnikoff, H. I. – Wells, R. O. Jr. (1973): Mathematics and civilization. Holt, Rinehart and Winston, Inc., New York, reprinted with additions 1984 Dover Publictions, Inc., Mineola, NY.
Rindler, W (1977): Essential relativity. Springer-Verlag, New York.
Rindler, W (1982): Introduction to special relativity. Clarendon Press, Oxford.
Robinson, R. M. (1971): Undecidability and nonperiodicity for tilings of the plane. Invent. Math. 12, 177–209.
Rouse Ball, W. W. (1892): Calculating prodigies. In Mathematical recreations and essays.
Rucker, R. (1984): Infinity and the mind: the science and philosophy of the infinite. Paladin Books, Granada Publishing Ltd., London (first published by Harvester Press Ltd., 1982).
Sachs, R. K. (1962): Gravitational waves in general relativity. VIII. Waves in asymptotically flat space-time. Proc. Roy. Soc. (London) A270, 103–26.
Schank, R. C. – Abelson, R. P. (1977): Scripts, plans, goals and understanding. Erlbaum, Hillsdale, NJ.
Shechtman, D. et al. (1984): Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 53, 1951.
Schrödinger, E. (1935): Die gegenwärtige Situation in der Quantenmechanik, Naturwissenschaften 23, 807–12, 823–8, 844–9. (Translation by J. T. Rimmer (1980). In Proc. Amer. Phil. Soc. 124, 323–38.) In Quantum theory and measurement (ed. J. A. Wheeler and W. H. Zurek). Princeton University Press, Princeton, NJ. 1983.
Schrödinger, E. (1967): ‘What is life?’ and ‘Mind and matter’. Cambridge University Press, Cambridge.
Searle, J. (1980): Minds, brains and programs. In The behavioral and brain sciences, Vol. 3. Cambridge University Press, reprinted in The mind’s I (ed. D. R. Hofstadter and D. C. Dennett). Basic Books, Inc., Penguin Books Ltd., Harmondsworth, Middx. 1981.
Searle, J. R. (1987): Minds and brains without programs. In Mindwaves (ed. C. Blakemore and S. Greenfield). Basil Blackwell, Oxford.
Smith, S. B. (1983): The great mental calculators. Columbia University Press.
Smorynski, C. (1983): „Big” news from Archimedes to Friedman. Notices Amer. Math. Soc. 30, 251–6.
Sperry, R. W. (1966): Brain bisection and consciousness. In Brain and conscious experience (ed. J. C. Eccles). Springer-Verlag, New York.
Squires, E. (1985): To acknowledge the wonder. Adam Hilger Ltd., Bristol.
Squires, E. (1986): The mystery of the quantum world. Adam Hilger Ltd., Bristol.
Stewart, I. (1991): A matematika problémái (Problems of mathematics, fordította Freud R.). Akadémiai Kiadó, Budapest.
Tipler, E J. – Clarke, C. J. S. – Ellis, G. F. R. (1980): Singularities and horizons – a review article. In General relativity and gravitation (ed. A. Held), Vol. 2, pp. 97–206. Plenum Press, New York.
Turing, A. M. (1937): On computable numbers, with an application to the Entscheidungsproblem. Proc. Lond. Math. Soc. (ser. 2) 42, 230–65; jay. 43, 544–6.
Turing, A. M. (1939): Systems of logic based on ordinals. Proc. Lond. Math. Soc. 45, 161–228.
Turing, A. M. (1950): Computing machinery and intelligence. Mind 59 no. 236; reprinted in The mind’s I (ed. D. R. Hofstadter and D. C. Dennett). Basic Books, Inc.; Penguin Books, Ltd; Harmondsworth, Middx. 1981.
Waltz, D. L. (1982): Artificial intelligence. Scientific American 247(4), 101–22.
Ward, R. S. – Wells, R. O. Jr. (1989): Twistor geometry. Cambridge University Press, Cambridge.
Weinberg, S. (1977). The first three minutes: A modern view of the origin of the universe. Andre Deutsch, London.
Weiskrantz, L. (1987): Neuropsychology and the nature of consciousness. In Mindwaves (ed. C. Blakemore and S. Greenfield). Blackwell, Oxford.
Westfall, R. S. (1980): Never at rest, Cambridge University Press, Cambridge.
Wheeler, J. A. (1983): Law without law. In Quantum theory and measurement (ed. J. A. Wheeler and W. H. Zurek). Princeton University Press, Princeton, NJ. pp. 182–213.
Wheeler, J. A. – Feynman, R. P. (1945): Interaction with the absorber as the mechanism of radiation. Rev. Mod. Phys. 17, 157–81.
Wheeler, J. A. – Zurek, W. H. (ed.) (1983): Quantum theory and measurement. Princeton University Press, Princeton, NJ.
Whittaker, E. T. (1910): The history of the theories of aether and electricity. Longman, London.
Wigner, E. P. (1960): The unreasonable effectiveness of mathematics. Commun. Pure Appl. Math. 13, 1–14.
Wigner, E. P. (1961): Remarks on the mind-body question. In The scientist speculates (ed. I. J. Good). Heinemann, London. (Reprinted in E. Wigner (1967): Symmetries and reflections, Indiana University Press, Bloomington) In Quantum theory and measurement (ed. J. A. Wheeler and W. H. Zurek). Princeton University Press, Princeton, NJ. 1983.
Will, C. M. (1987): Experimental gravitation from Newton’s Principia to Einstein’s general relativity. In 300 years of gravitation (ed. S. W. Hawking and W. Israel). Cambridge University Press, Cambridge.
Wilson, D. H. et al. (1977): Cerebral commissurotomy for the control of intractable seizures. Neurology 27, 708–15.
Winograd, T. (1982): Understanding natural language. Cognitive Psychology 3, 1–191.
Wootters, W. K. – Zurek, W. H. (1982): A single quantum cannot be cloned. Nature 299, 802–3.
Képesek vagyunk a retinánkba bevágódó egyetlen fotont érzékelni. de ami nagyon különös, az agy - mint tudatos szemlélő - ennek az adott pillanatban (még) nincs tudatában.
Igen, ez az egy foton és az agy; az idő, ami nem is
folyik, csak van. Ez az ami megfogott a könyvben. Az egy fotonnyi villanások,
amelyek aztán megfelelő – tudatos agyműködés létrehozására alkalmas –kritikus tömeget
átlépve elindítanak valamit bennünk: egy érzést, gondolatot, „ihletet”, „meglátást”
(Penrose szavaival), vagy felszínre hoznak rég megtörtént dolgokat, emlékeket.
Igen, ez az egy foton és az agy; az idő, ami nem is
folyik, csak van. Ez az ami megfogott a könyvben. Az egy fotonnyi villanások,
amelyek aztán megfelelő – tudatos agyműködés létrehozására alkalmas –kritikus tömeget
átlépve elindítanak valamit bennünk: egy érzést, gondolatot, „ihletet”, „meglátást”
(Penrose szavaival), vagy felszínre hoznak rég megtörtént dolgokat, emlékeket.

















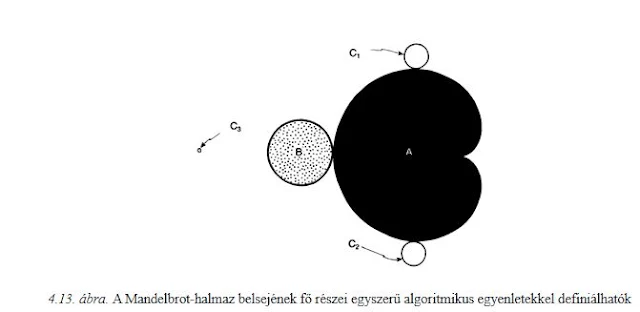









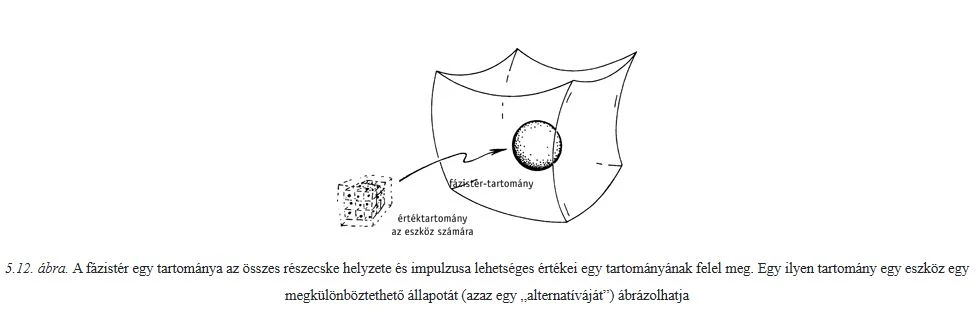






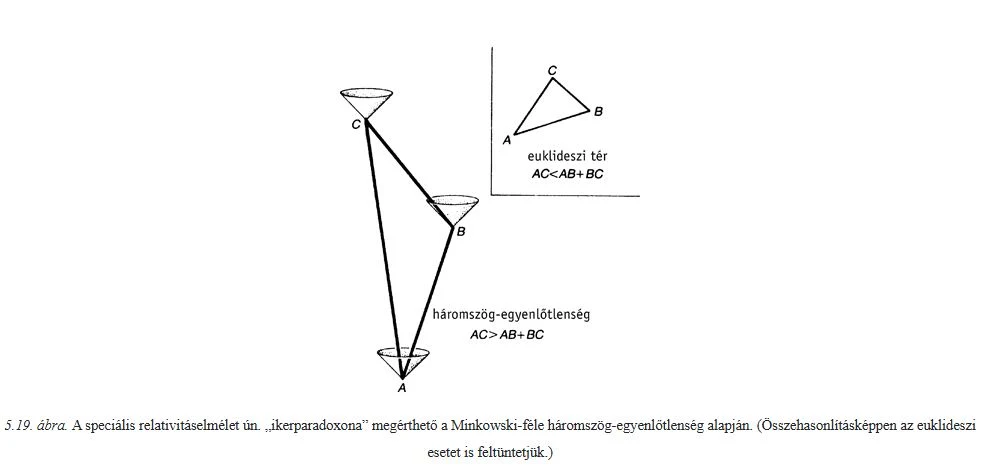










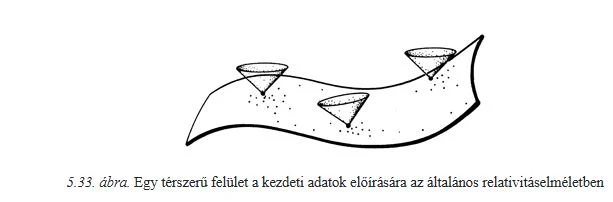




























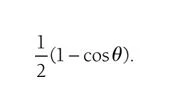












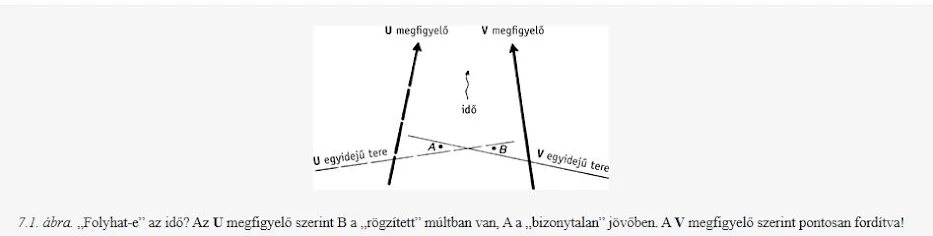







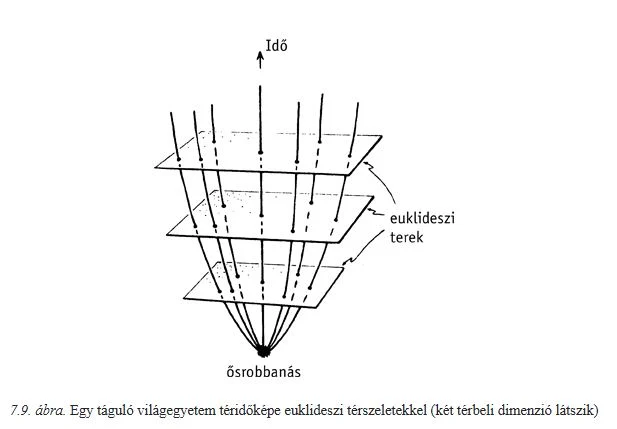






















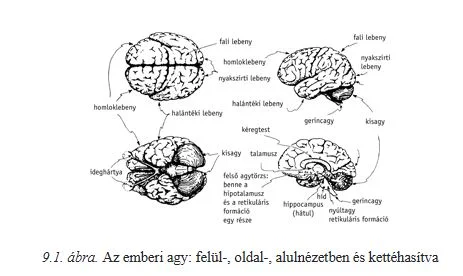
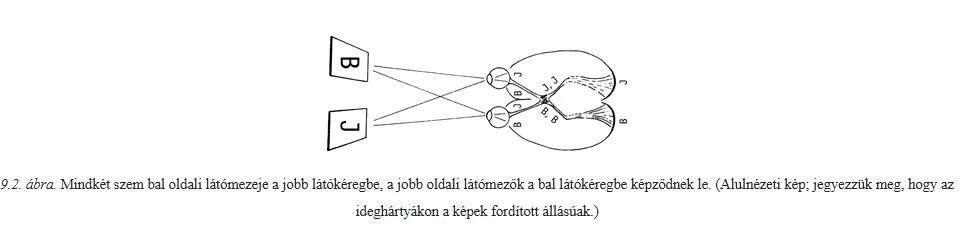



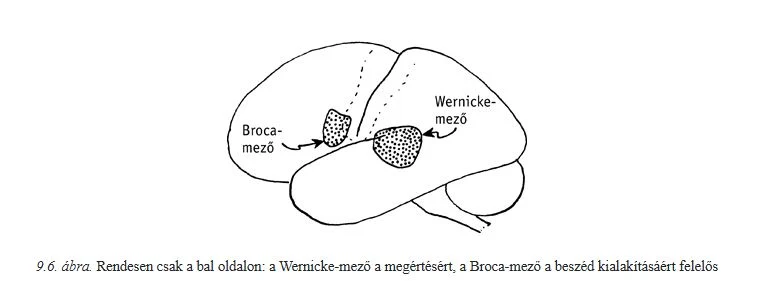







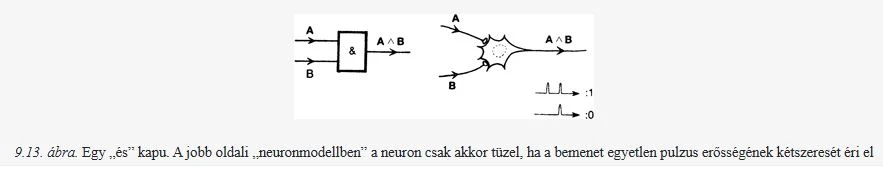





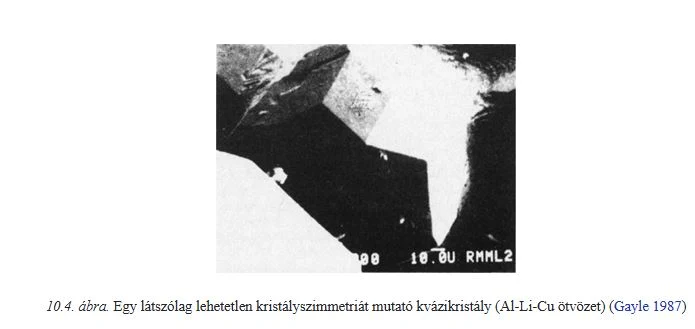



Megjegyzések